Ejercicios Examen Teoría DLP 🐲

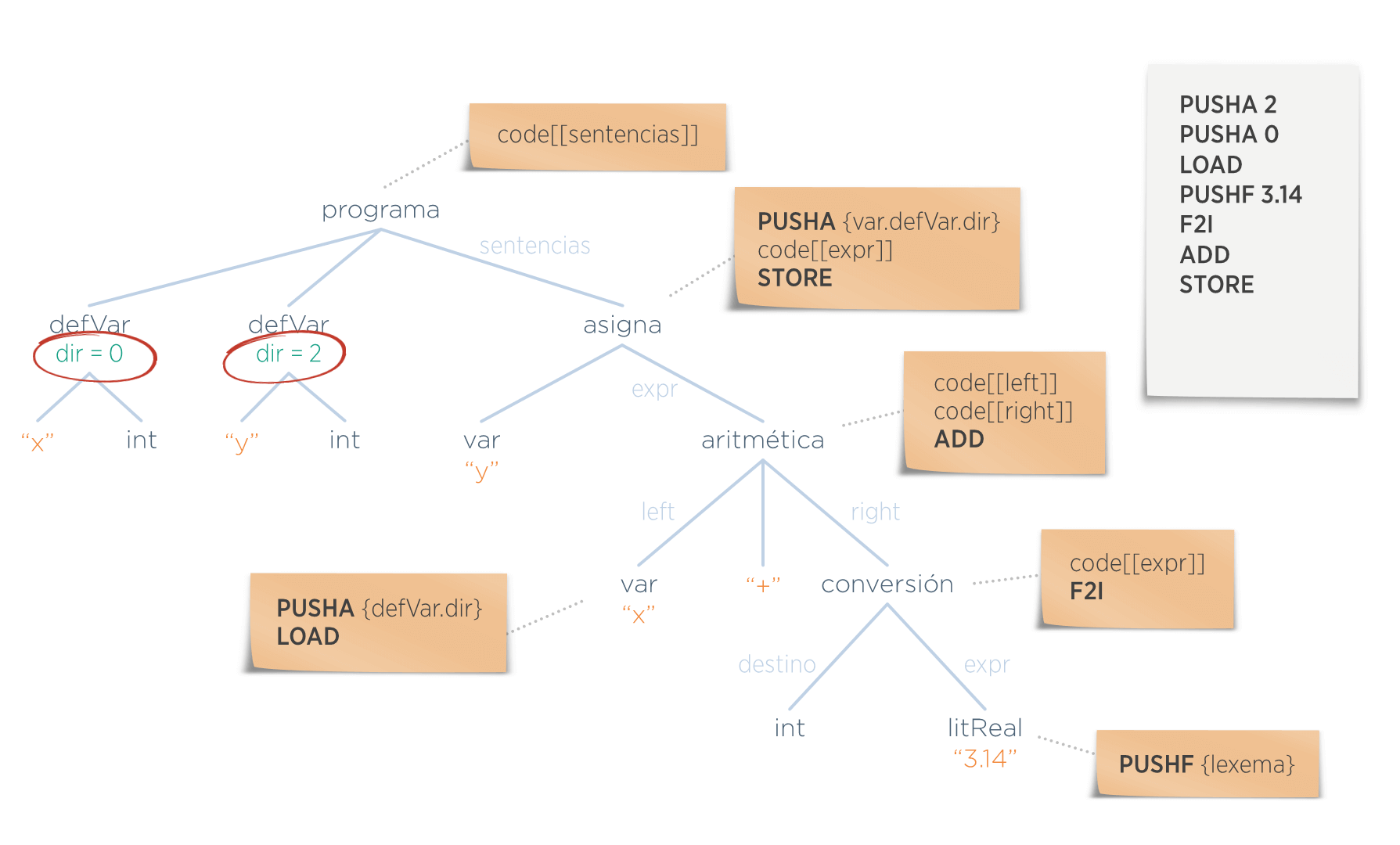
Ejemplo 110: La entrada a traducir es la siguiente, implementada en un lenguaje ficticio al estilo C.

int x, y;
y = x + (int) 3.14;

• Léxico: encontrar todos los tokens
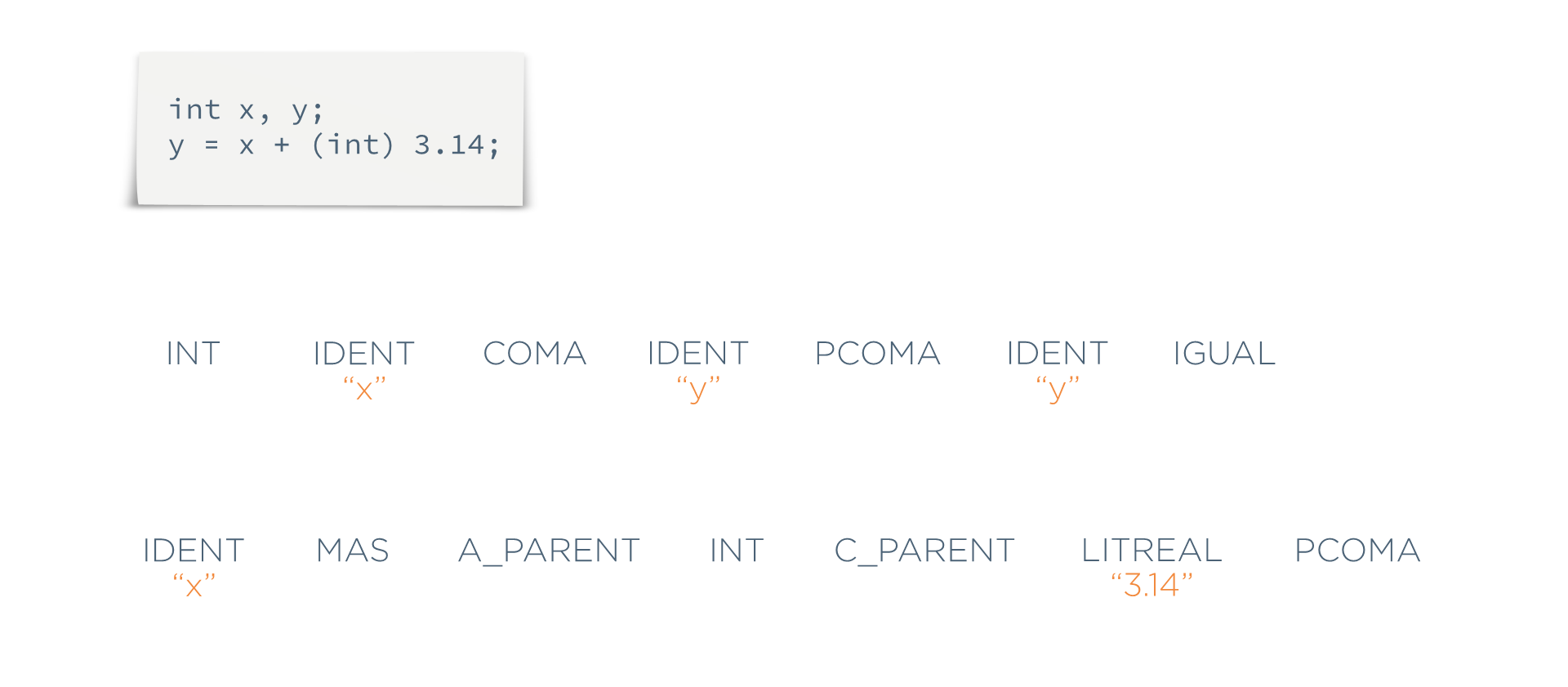
• Sintáctico: una vez tenemos los tokens, mostrar el AST
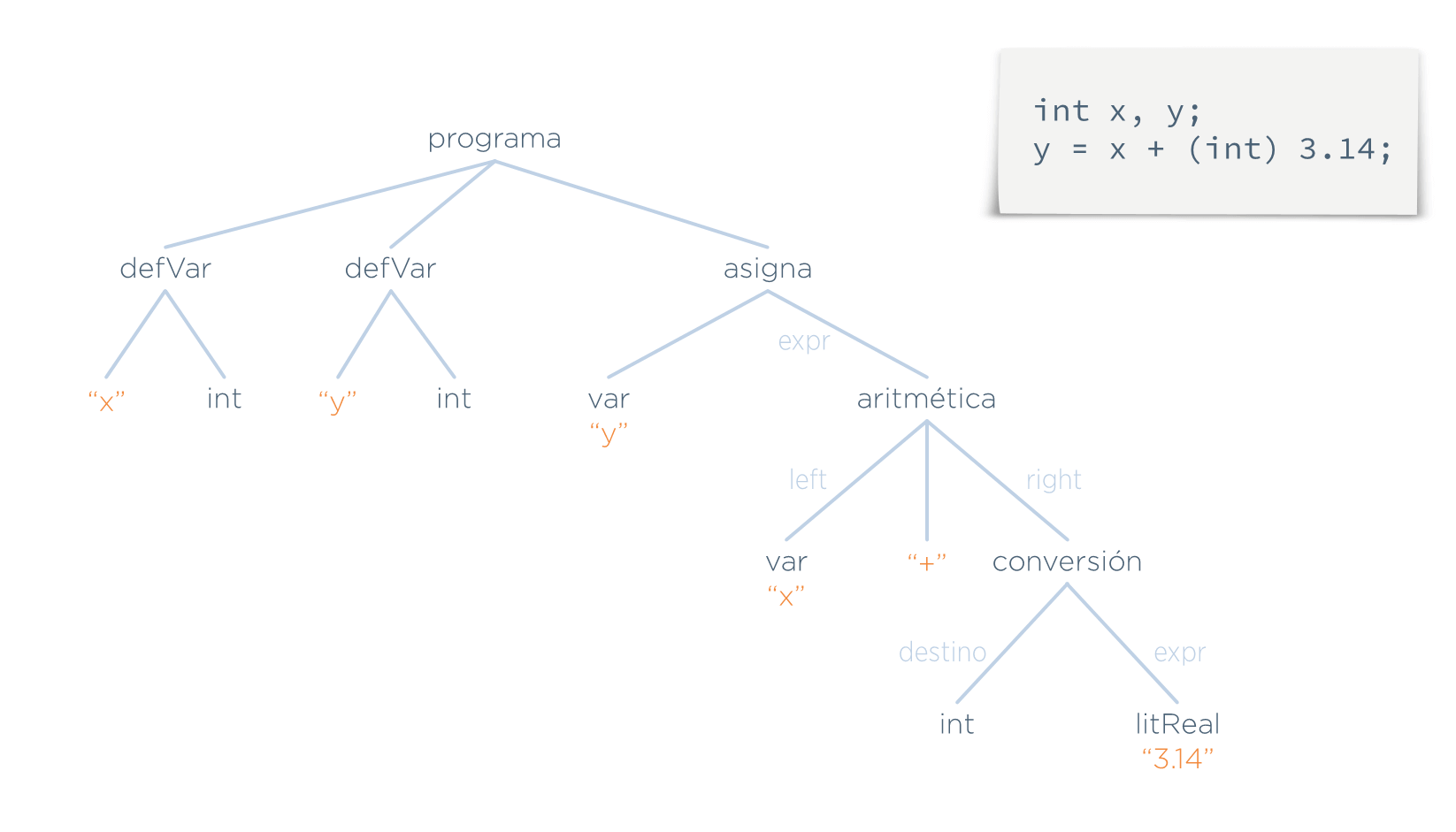
• Semántico: validar el AST
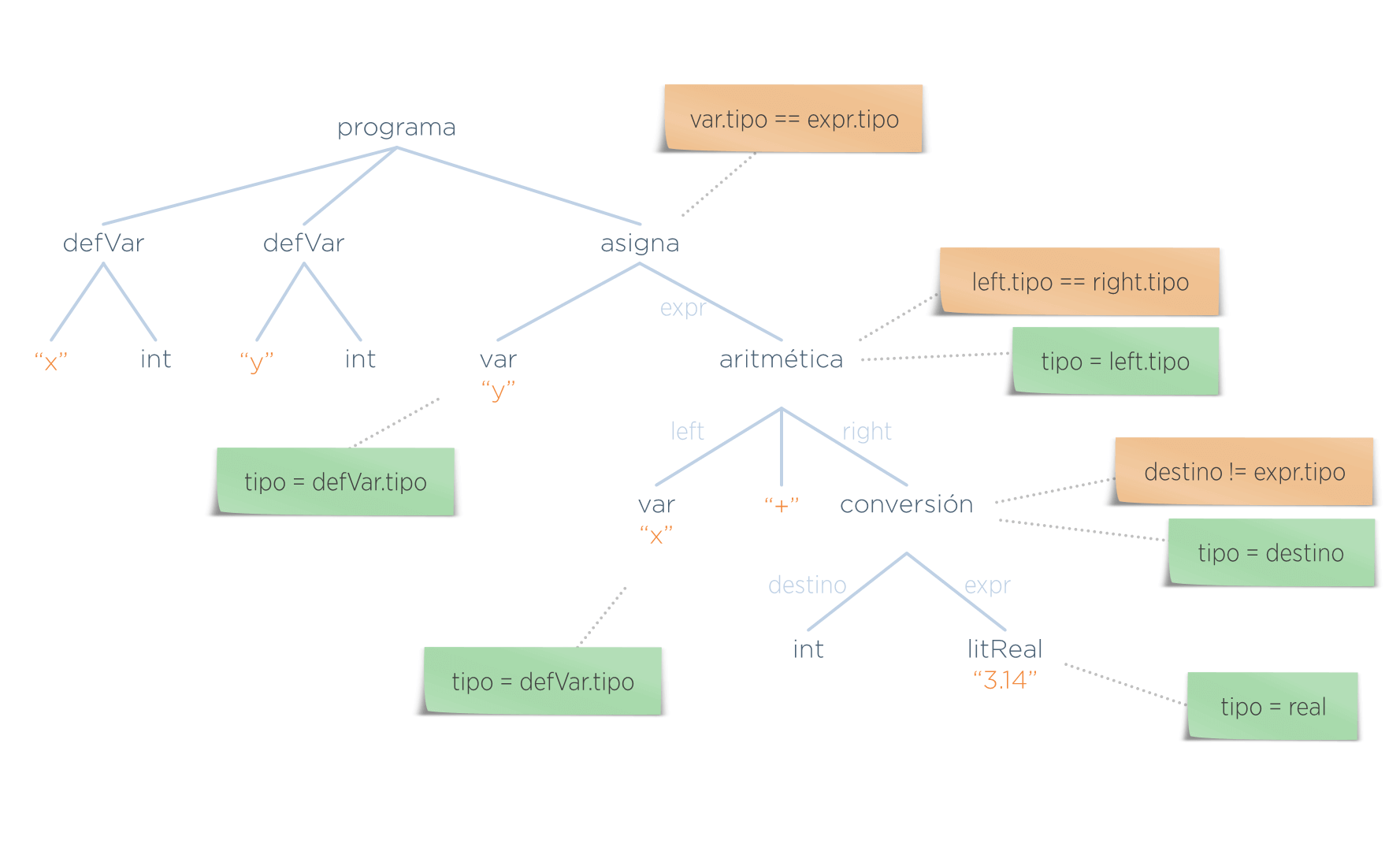
• Generación de código: generar el código resultante

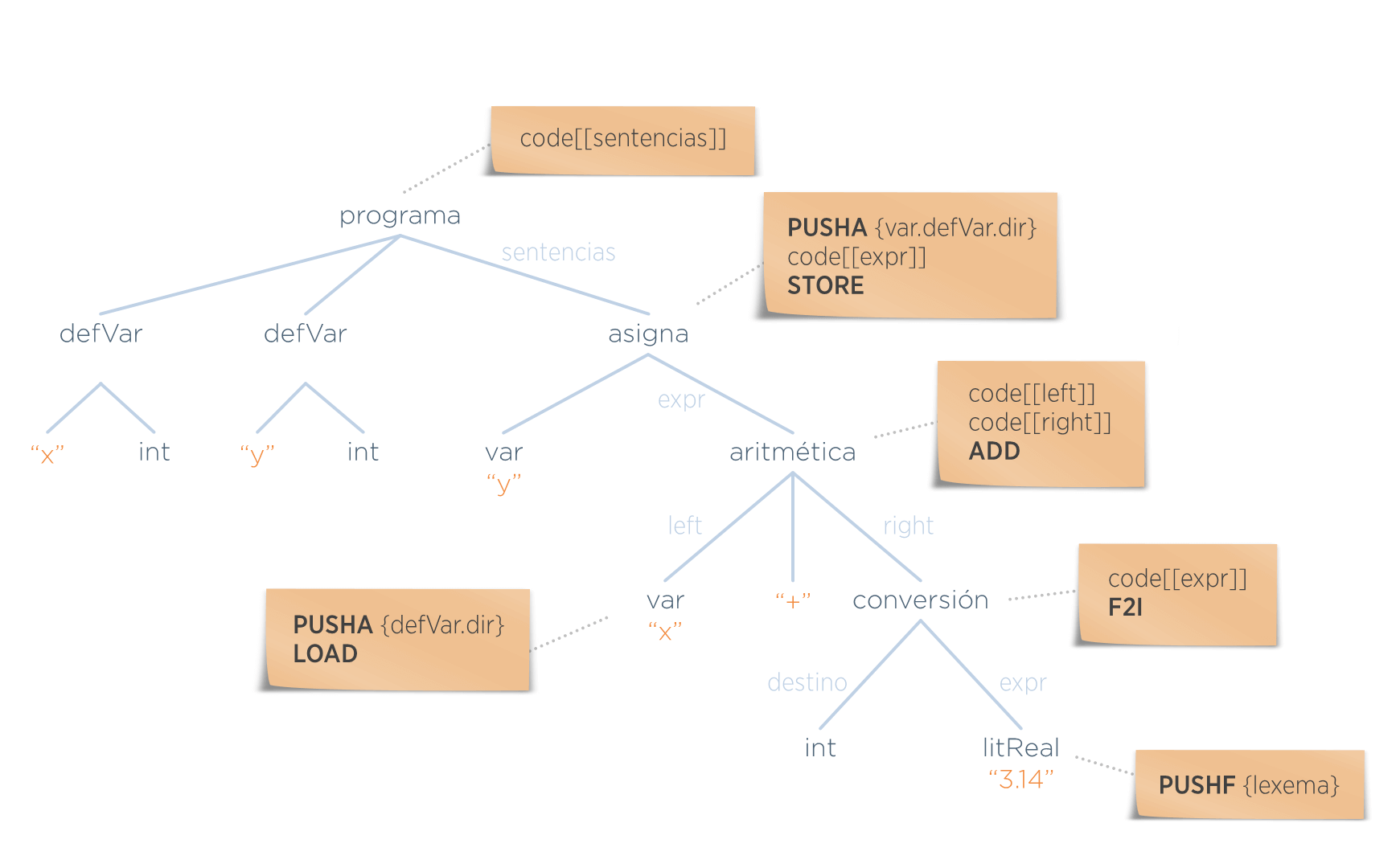
Léxico

2. Supóngase un programa:

Lexico lex = new Lexico(new FileReader(“prog.txt"));
Token token;
while ((token = lex.nextToken()).getType() != Lexico.END) {
    System.out.println(token.getLexeme());
    System.out.println(token.getType());
    System.out.println(token.getLine());
}

Ahora supóngase la siguiente entrada:

altura
+
1.75

Y finalmente, supóngase que se han definidos las siguientes constantes asociadas a los tokens del lenguaje:

class Lexico {
    static final int END = 0;
    static final int IDENT = 257;
    static final int IF = 258;
    static final int LITENT = 259;
    static final int LITREAL = 260;
    …
}

El resultado es:

	(getLexema, getTipo, getLinea)
1	(“altura”, 257, 1)
2	(”+”, 261, 2)
3	(“1,75”, 260, 3)
4	(?, 0, 2)

Nota: el ? indica EOF

3. Hacer el analizador léxico del siguiente lenguaje usando ANTLR.

edad = 65;	 # Comentario de una línea
print a
read b;
print "fin"

IGUAL: '=';
PCOMA: ';';
 
PRINT: 'print';
READ: 'read';
 
LITENT: [0-9]+;
IDENT: [a-zA-Z]*[a-zA-Z0-9]*;
 
STRING: '"' (~[\r\n])* '"';
 
COMMENT: '#'.*? '\n' -> Skip; //CON EL OPERADOR NON-GREEDY
COMMENT: '#' ~[\r\n]* -> Skip; //SIN EL OPERADOR NON-GREEDY
 
WS: [ \t\r\n]+ -> skip;

---

Sintáctico

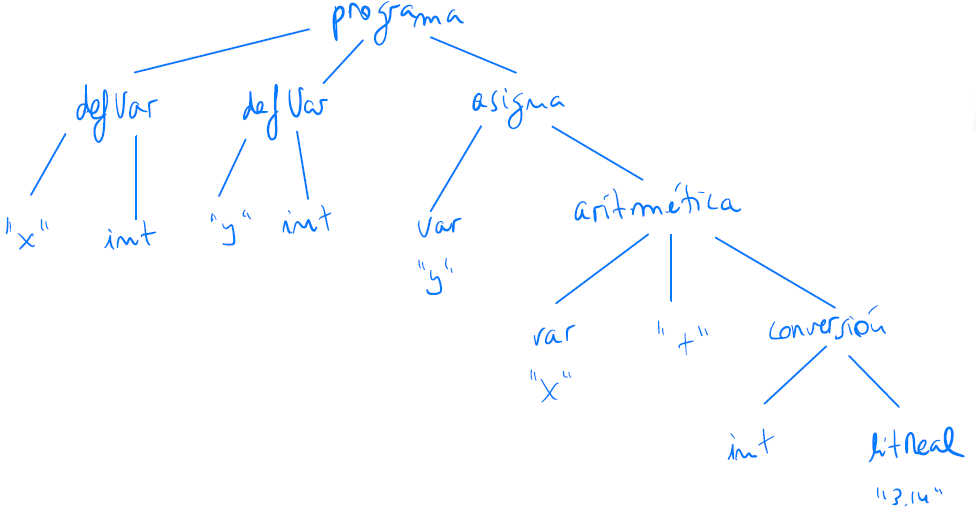
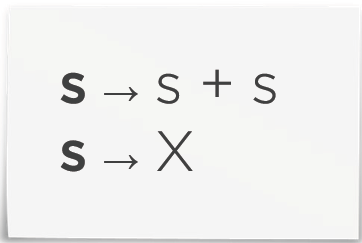
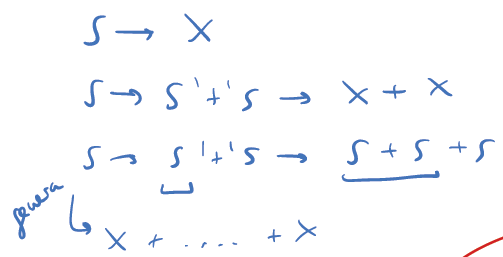
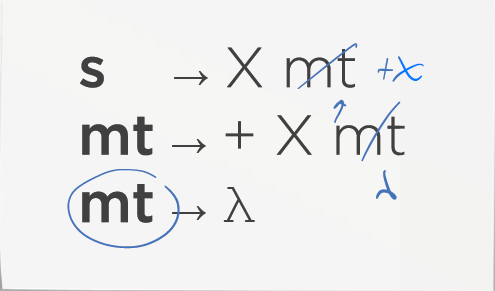
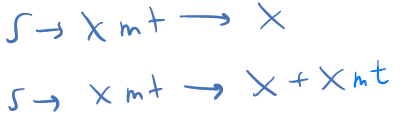
NOTA: los ejs 2 y 3 son gramáticas equivalentes

4. Decir si es una sentencia válida Si realizamos las correspondientes transformaciones:

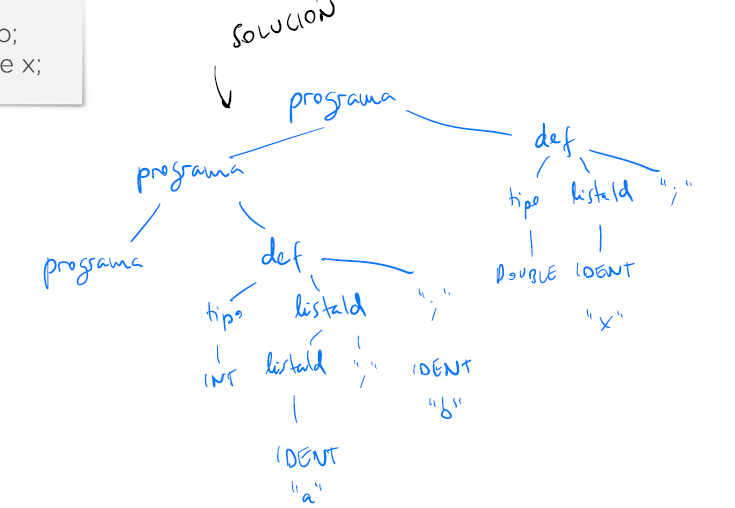
5. Dada la siguiente gramática G: (IGUAL QUE EL 4)

programa ⟶ programa def
        | ε
 
def ⟶ tipo listaId ‘;’
 
tipo ⟶ INT | DOUBLE
 
listaId ⟶ IDENT
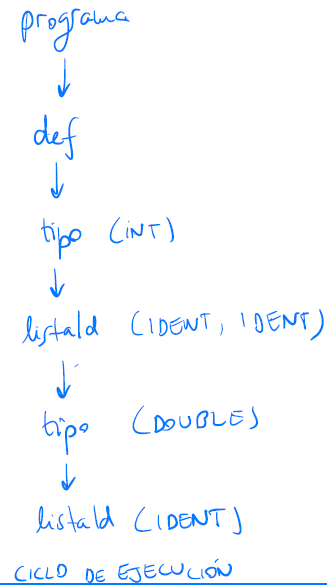
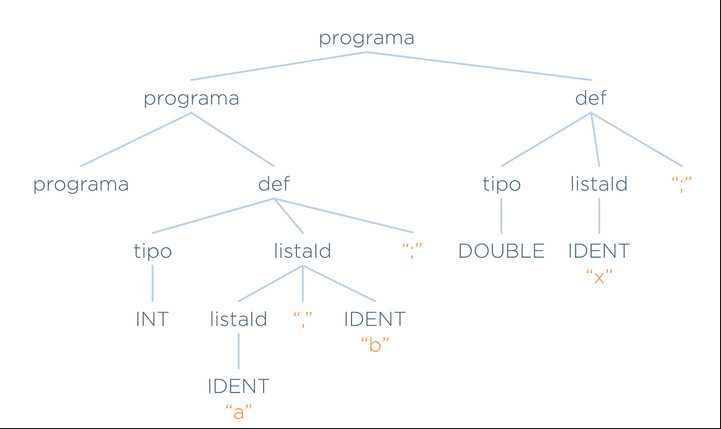
        | listaId ‘,’ IDENT

Determinar si la siguiente entrada es válida. En caso afirmativo, construir su árbol de análisis gramatical (árbol concreto).

int a, b;
double x;

Si que es válida, pues se puede llegar a la cadena realizando transformaciones a partir de programa

6. Dada la siguiente gramática, implementar un parser de la misma utilizando la técnica recursiva descendente.

prog ⟶ decl decl
 
decl ⟶ variables | typedef
 
variables ⟶ VAR IDENT restoIdents
 
restoIdents ⟶ ‘,’ IDENT restoIdents
	     | ‘:’ tipo
 
tipo ⟶ INT | FLOAT
 
typedef ⟶ TYPE IDENT restoIdents

Solución:

public class RecursiveParser {
    private Lexicon lex;
    private Token token;
	
	public RecursiveParser(Lexicon lex) throws ParseException{
		this.lex = lex;
		advance();
	}
 
	private void advance(){
		tokent = lex.nextToken();
	}
 
	private void error() throws ParseException{
		throw new ParseException("Error sintáctico.");
	}
 
	void match(int tokenType) throws ParseException{
		if(token.getType() == tokenType)
			advance();
		else
			error();
	}
 
	//--------
 
    public void prog() throws ParseException {
        decl();
        decl();
        match(Lexicon.EOF);
    }
 
    void decl() throws ParseException {
        if (token.getType() == Lexicon.VAR)
            variables();
        else if (token.getType() == Lexicon.TYPE)
            typedef();
        else
            error();
    }
 
    void variables() throws ParseException {
        match(Lexicon.VAR);
        match(Lexicon.IDENT);
        restoIdents();
    }
 
    void restoIdents() throws ParseException {
        if (token.getType() == Lexicon.COMA) {
            match(Lexicon.COMA);
            match(Lexicon.IDENT);
            restoIdents();
        } else if (token.getType() == Lexicon.PUNTOS) {
            match(Lexicon.PUNTOS);
            tipo();
        } else
            error();
    }
 
    void tipo() throws ParseException {
        if (token.getType() == Lexicon.INT)
            match(Lexicon.INT);
        else if (token.getType() == Lexicon.FLOAT)
            match(Lexicon.FLOAT);
        else
            error();
    }
 
    void typedef() throws ParseException{
        match(Lexicon.TYPE);
        match(Lexicon.IDENT);
        restoIdents();
    }
}

7. Hacer una especificación ANTLR para un lenguaje con las siguientes características:

Solución:

• Primero implementamos el léxico del lenguaje:

lexer grammar Lexicon;

NUM : [0-9]+;
IDENT : [a-zA-Z0-9_]+;

WS : [ \t\r\n]+ -> skip;

• Ahora la gramática:

grammar Grammar;
 
import Lexicon;
 
start : 'print' expr ';';
 
expr:
	NUM
	| IDENT
	| '(' expr ')'
	| expr ('*' | '/') expr
	| expr ('+' | '-') expr
	| expr ('==' | '!=') expr
	| expr '&&' expr
	| expr '||' expr
	;

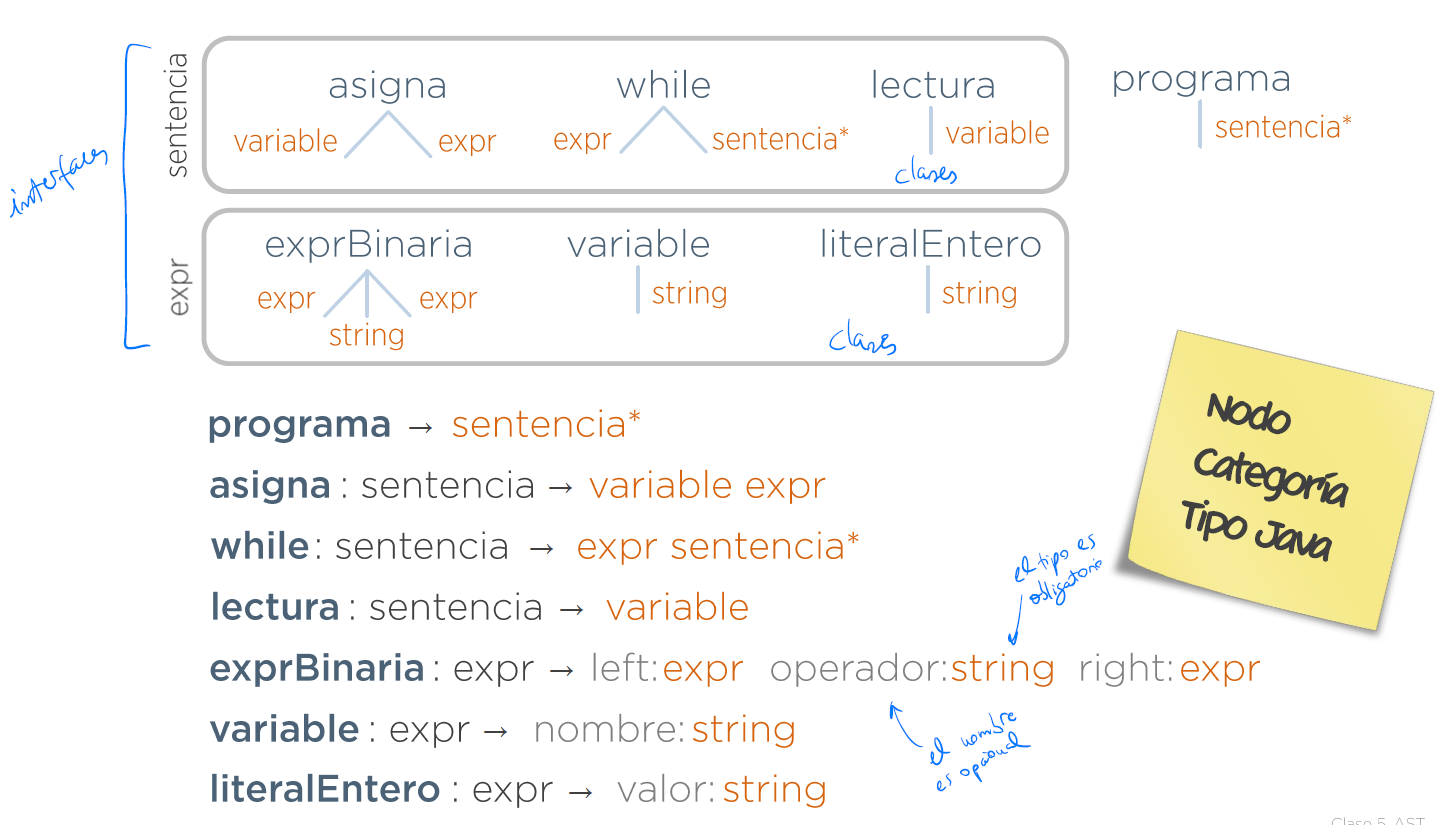
9. Describir los nodos que hay y decir qué hijos tiene cada uno. Crear la gramática abstracta para el lenguaje del ejemplo. Solución:

programa ⟶ defVariable* sentencia*
defVariable ⟶ nombre:string tipo
 
intType:tipo ⟶  ε
realType:tipo ⟶ ε
 
escritura:sentencia ⟶ expresion
if:sentencia ⟶ condicion:expresión cierto:sentencia* falso:sentencia*
 
exprBinaria:expresion ⟶ left:expresión operator:string right:expresion
invocacion:expresion ⟶ nombre:string args:expresion*
variable:expresion ⟶ lexema:string
literalInt:expresion ⟶ lexema:string
literalReal:expresion ⟶ lexema:string

10. Dada la siguiente especificación sintáctica en ANTLR y la gramática abstracta que define los nodos del AST, añadir la especificación de ANTLR el código que cree el AST de las entradas: Abstracta:

programa ⟶ definicion print;

definicion ⟶ tipo nombre:string;

tipoInt:tipo ⟶  ;
tipoReal:tipo ⟶ ;

print ⟶ expr:expresion;

variable:expresion ⟶ nombre:string;
literalEntero:expresion ⟶ valor:string;

Gramática

start
	: definicion print EOF
	;
 
definicion
	: tipo IDENT ';'
	;
 
tipo
	: 'int'
	| 'float'
	;
 
print
	: 'print' expr ';'
	;
 
expr
	: IDENT
	| LITENT
	;

Solución: El parser sería:

@parser::header {
    import ast.*;
}
 
start returns[Programa ast]
	: definicion print EOF { $ast = new Programa($definicion.ast, $print.ast); }
	;
 
definicion returns[Definicion ast]
	: tipo IDENT ';' { $ast = new Definicion($tipo.ast, $IDENT.text); }
	;
 
tipo returns[Tipo ast]
	: 'int'		{ $ast = new TipoInt(); }
	| 'float'	{ $ast = new TipoReal();}
	;
 
print returns[Print ast]
	: 'print' expr ';' { $ast = new Print($expr.ast); }
	;
 
expr returns[Expresion ast]
	: IDENT		{ $ast = new Variable($IDENT.text); }
	| LITENT	{ $ast = new LiteralEntero($LITENT.text); }
	;

11. Dada la siguiente gramática:

programa: sent*
sent: PRINT expr ';'
expr: IDENT
	| INT_CONSTANT
	| expr '*' expr
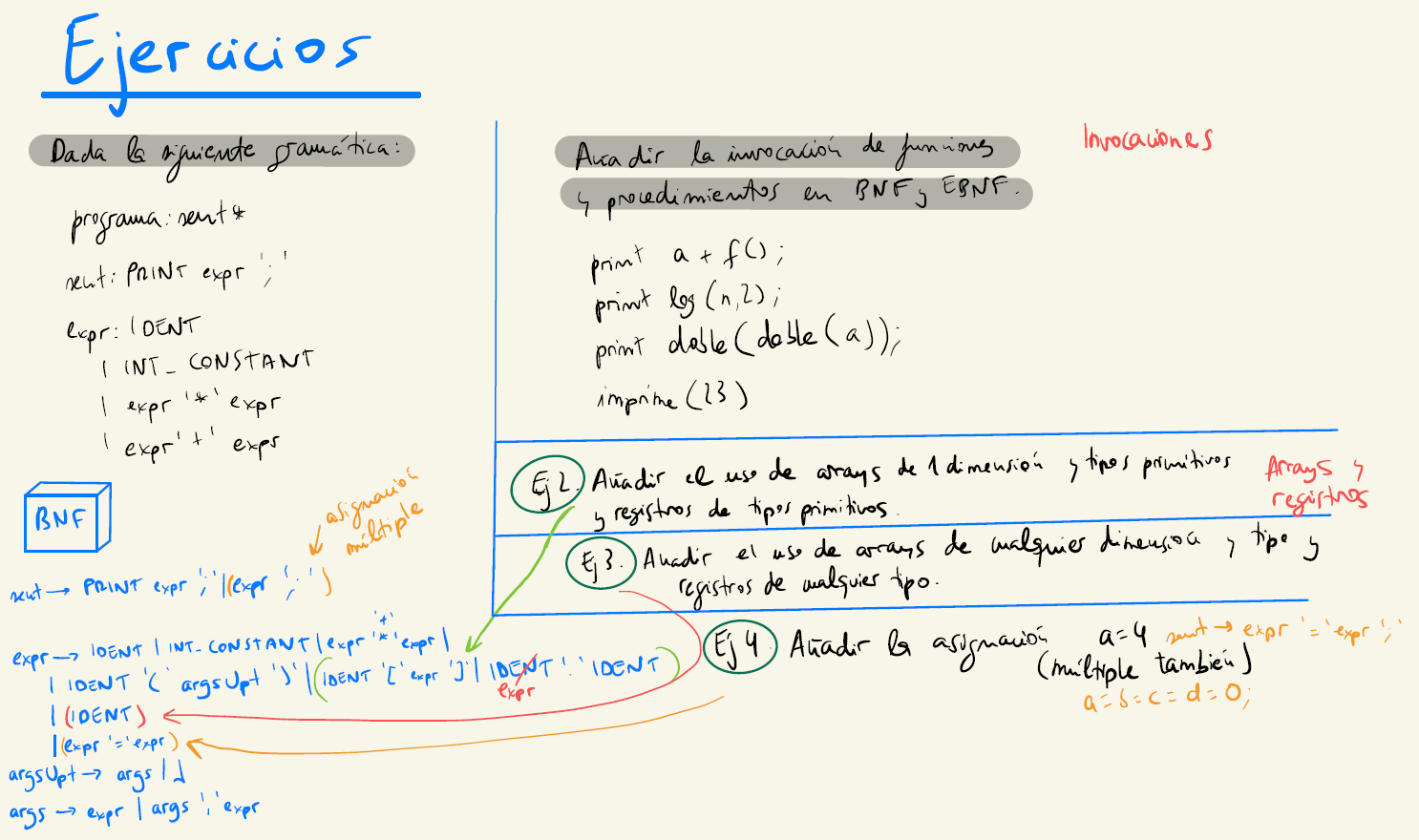
	| expr '+' expr

a) Añadir la invocación de funciones y procedimientos en BNF y EBNF. Ejemplos:

• print a+f();
• print log(n,2);
• print doble(doble(a));
• print (23) b) Añadir el uso de arrays de 1 dimensión y tipos primitivos y registros de tipos primitivos c) Añadir el uso de arrays de cualquier dimensión y tipo y registros de cualquier tipo d) Añadir la asignación a=4 (múltiple)

Solución:

programa: sent*
sent: PRINT expr ';'
	| expr ';' //asignación múltiple
expr: IDENT
	| INT_CONSTANT
	| expr '*' expr
	| expr '+' expr
	| IDENT '(' expr ')' //invocación a funciones
	| IDENT '[' expr ']' //arrays de cualquier dimensión
	| expr '=' expr //asignación simple
	

12. Hacer una gramática en BNF de un lenguaje con las siguientes características:

• Un conjunto está formado por uno o más elementos entre paréntesis separados por comas.
• Cada elemento puede ser un número u otro conjunto.
• Los números están formados por dígitos de 1 al 3, pudiendo haber espacios entre ellos. Suponer que el analizador léxico devuelve los tokens UNO, DOS y TRES.
• Los números están formados por un número impar de dígitos y son capicúa.

Ejemplos de entradas válidas serían:

(131)
(3, 222, 12 313)
(12121, 2, (333), (2, 3, 1111111))
(2132312, ( ( (1, 2), 2, 131), 1, 2), 3322233)

Se pide hacer una gramática BNF usando las construcciones anteriores. Anotar en cada regla qué construcción sigue.

Solución: La gramática pedida sería:

conjunto: '(' elementos ')'                     // Secuencia
 
elementos: elemento | elementos ‘,’ elemento    // Lista
elemento: num | conjunto                        // Dos secuencias
 
num: UNO            // Composición
    | DOS
    | TRES
    | UNO num UNO
    | DOS num DOS
    | TRES num TRES

13. Sea un lenguaje para la definición de variables.

int a, b;
double x;

Requisitos:

• Sólo hay dos tipos: entero (int) y real (double).
• En una sola definición, pueden definirse varias variables del mismo tipo.
• En un programa puede haber varias definiciones, pero también sería válido que no hubiera ninguna.

Se pide especificar la sintaxis de dicho lenguaje en BNF y en EBNF. Indicar, además, los patrones usados en las listas.

Solución BNF

Aplicando los patrones anteriores y sustituyendo sus símbolos por los nombres adecuados para este ejercicio, quedaría finalmente esta gramática.

definiciones: ε | definiciones definicion       // lista 0+ss
definicion: tipo nombres ';'                    // secuencia
nombres: IDENT | nombres ',' IDENT              // lista 1+cs

Como puede verse, toda regla sigue alguna de las tres construcciones básicas. Lo cual, a medida que el alumno se familiarice con ellas, hará que cada vez le será más fácil entender y crear cualquier gramática.

En el caso concreto de las listas (reglas 1 y 3) se han aplicado los patrones correspondientes a la versión recursiva a izquierda.

Solución EBNF

La solución en EBNF sería:

definiciones: definicion*           // lista 0+ss
definicion: tipo nombres ';'        // secuencia
nombres: IDENT (',' IDENT)*         // lista 1+cs

Como puede verse, las construcciones son las mismas, sólo que en el caso de las listas se han tomado los patrones de otra columna de la tabla (la última).

14. Sea la siguiente gramática ambigua.

expr ⟶ expr '+' NUM
    | NUM
    | '(‘ tipo ')' expr 	// Suponemos tipo definido

Se pide:

1. Demostrar que es ambigua.
2. Dar una solución no ambigua con cambio de lenguaje y otra usando reglas de selección en ANTLR.

Solución

1. Demostrar que es Ambigua

Tal y como se dijo anteriormente, no existe un algoritmo que dada una gramática cualquiera indique si es ambigua o no. Pero una forma de demostrar que una gramática en particular sí es ambigua es mostrar una entrada para la cual al menos se puedan crear dos árboles concretos (es decir, que haya dos formas de interpretarla).

Una entrada que demostraría que la gramática es ambigua sería la siguiente:

(double) 3 + 4

Esta entrada puede producir dos árboles concretos (es decir, se puede llegar del símbolo inicial a la cadena mediante dos caminos) ya que hay dos formas de interpretarla:

En el primer árbol se interpreta que primero se convierte el 3 a double y al resultado de la conversión se suma al 4. En el árbol de la derecha se interpreta que primero hay que sumar y luego realizar la conversión de todo ello.

Por tanto, la gramática es ambigua.

2. Solución con Cambio de Lenguaje

Se podría cambiar el lenguaje para que el valor sobre el que se realiza la conversión tuviera que estar delimitado, por ejemplo, con ’<’ y ’>‘. En esta caso, ya no habría dos formas de interpretar la entrada:

expr ⟶ expr '+' NUM
    | NUM
    | '(' tipo ')' '<' expr '>'

Las entradas dejarían claro el alcance de la conversión:

(double)<3 + 4>

(double)<3> + 4

Solución con Reglas de Selección

En vez de cambiar el lenguaje, se puede dejar como está y, dejando la gramática ambigua, determinar qué derivación (interpretación) se quiere para dichas entradas.

De los dos árboles que generaba la entrada anterior, lo habitual es que se quiera interpretar que primero se hace la conversión y luego la suma, es decir, que la conversión tenga mayor prioridad. Por tanto, se quiere seguir la derivación que se corresponda con el árbol de la izquierda.

Para ello, en ANTLR habría que dar mayor prioridad (poner primero) la regla de la conversión y luego la de la suma.

expr ⟶ NUM
    | '(' tipo ')' expr
    | expr '+' NUM

Solución con Gramática Equivalente

Aunque no se ha pedido en el enunciado, por si se tiene curiosidad, aquí estaría la solución hallando una gramática equivalente que no es ambigua.

expr ⟶ termino
    	| expr + termino
 
termino ⟶ factor
	    | '(' type ')' termino
 
factor ⟶ NUM

14. Hacer una especificación en ANTLR para un lenguaje con las siguientes características:

• Una entrada tendrá sólo una única sentencia ‘print’ seguida de una expresión y un punto y coma.
• Características de las expresiones:
  • Operadores relacionales: '==' y '!='.
  • Operadores lógicos: ’||’ y ’&&’ (or y and respectivamente).
  • Operadores aritméticos: ’+’, ’-’, ’*’ y ’/‘.
  • Agrupación de expresiones entre paréntesis.

Ejemplos de entradas válidas en este lenguaje serían:

print a + 2 == 3 && a / 5 != b;
print a * (4 - 2);

Solución: Lo primero, habría que hacer el léxico del lenguaje.

lexer grammar Lexicon;
 
NUM : [0-9]+;
IDENT : [a-zA-Z0-9_]+;
 
WS : [ \t\r\n]+ -> skip;

Y a continuación se haría la gramática.

grammar Grammar;
 
import Lexicon;
 
start : 'print' expr ';';
 
expr:
	NUM
	| IDENT
	| '(' expr ')'
	| expr ('*' | '/') expr
	| expr ('+' | '-') expr
	| expr ('==' | '!=') expr
	| expr '&&' expr
	| expr '||' expr
	;

Nótese cómo el orden de las reglas corresponde con la prioridad de los operadores (los operadores de la misma prioridad, por tanto, deben ir en la misma regla).

Supóngase la siguiente entrada válida.

print a + 2 == 3 && a / 5 != b;

Para dicha entrada, el árbol concreto que correspondería con la interpretación que hará ANTLR de la misma tal y como están ordenadas las reglas sería el siguiente. 15. Crear la gramática abstracta para el lenguaje del siguiente ejemplo:

double a;
 
if (a > 2) then
    print a;
else
    print g(5, a) + 8.3;
endif
 
print f(a * 2);

Aclaraciones:

• Hay sólo dos tipos: int y double.
• Las condiciones del if son de tipo entero (no hay tipo booleano).
• Las definiciones de las variables tienen que estar antes de todas las sentencias.
• Puede haber varias sentencias en cada rama del if.

Solución:

programa ⟶ defVariable* sentencia*
defVariable ⟶ nombre:string tipo
 
intType:tipo ⟶  ε
realType:tipo ⟶ ε
 
escritura:sentencia ⟶ expresion
if:sentencia ⟶ condicion:expresión cierto:sentencia* falso:sentencia*
 
exprBinaria:expresion ⟶ left:expresión operator:string right:expresion
invocacion:expresion ⟶ nombre:string args:expresion*
variable:expresion ⟶ lexema:string
literalInt:expresion ⟶ lexema:string
literalReal:expresion ⟶ lexema:string

16. Dada la siguiente especificación sintáctica en ANTLR y la gramática abstracta que define los nodos del AST, añadir a la especificación de ANTLR el código que cree en AST de las entradas.

programa ⟶ definicion print;
 
definicion ⟶ tipo nombre:string;
 
tipoInt:tipo ⟶  ;
tipoReal:tipo ⟶ ;
 
print ⟶ expr:expresion;
 
variable:expresion ⟶ nombre:string;
literalEntero:expresion ⟶ valor:string;

start
	: definicion print EOF
	;
 
definicion
	: tipo IDENT ';'
	;
 
tipo
	: 'int'
	| 'float'
	;
 
print
	: 'print' expr ';'
	;
 
expr
	: IDENT
	| LITENT
	;

Solución:

@parser::header{
	import ast.*
}
 
start returns[Programa ast]
	: definicion print EOF { $ast = new Programa($definicion.ast, $print.ast); }
	;
 
definicion returns[Definicion ast]
	: tipo IDENT ';' { $ast = new Definicion($tipo.ast, $IDENT.text); }
	;
 
tipo returns[Tipo ast]
	: 'int' { $ast = new tipoInt(); }
	| 'float' { $ast = new tipoReal(); }
	;
 
print returns[Print ast]
	: 'print' expr ';' { $ast = new Print($expr.ast); }
	;
 
expr returns[Expresion ast]
	: IDENT { $ast = new Variable($IDENT.text); }
	| LITENT { $ast = new LiteralEntero($LITENT.text); }
	;

17. Dada la gramática en ANTLR y la gramática abstracta siguientes, añadir al fichero de ANTLR las acciones que construyan el AST.

start
    : sentences EOF
    ;
 
sentences
    : sentence*
    ;
 
sentence
    : 'print' expr ';'
    | left=expr '=' right=expr ';'
    ;
 
expr
    : left=expr op=('*' | '/') right=expr
    | left=expr op=('+' | '-') right=expr
    | '(' expr ')'
    | IDENT
    ;

program → sentences:sentence*;
 
print:sentence → expression;
assignment:sentence → left:expresión right:expression;
 
arithmetic:expression → left:expresión operator:string right:expression;
variable:expression → name:string;

Solución:

start returns[Program ast]
    : sentences EOF { $ast = new Program($sentences.list); }
    ;
 
sentences returns[List<Sentence> list = new ArrayList<Sentence>()]
    : (sentence { $list.add($sentence.ast); })*
    ;
 
sentence returns[Sentence ast]
    : 'print' expr ';' { $ast = new Print($expr.ast); }
    | left=expr '=' right=expr ';' { $ast = new Assignment($left.ast, $right.ast); }
    ;
 
expr returns[Expression ast]
    : left=expr op=('*' | '/') right=expr { $ast = new Arithmetic($left.ast, $op.text, $right.ast); }
    | left=expr op=('+' | '-') right=expr { $ast = new Arithmetic($left.ast, $op.text, $right.ast); }
    | '(' expr ')' { $ast = $expr.ast; }
    | IDENT { $ast = new Variable($IDENT.text); }
    ;

---

Semántico

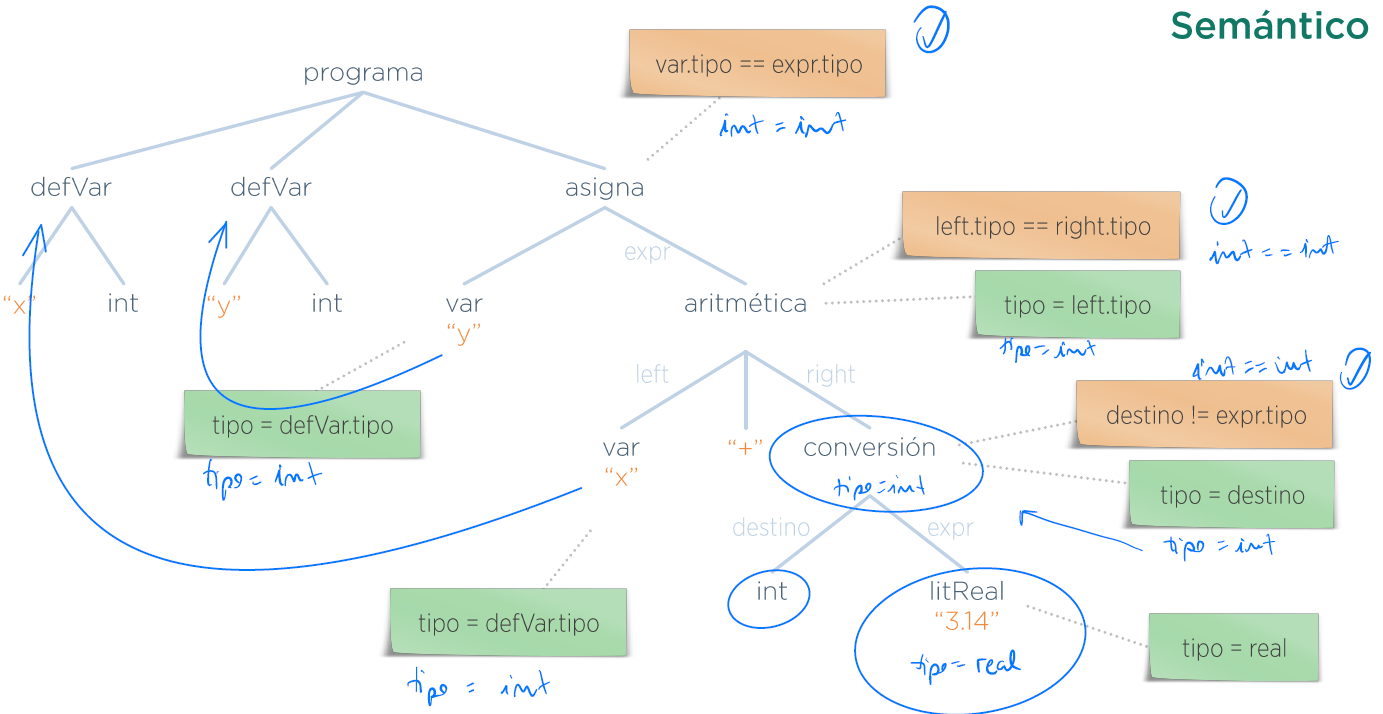
Solución: (G): (A): {expression.lvalue} dominio=booleano

(R):

(4) expression.lvalue = true
(5) expression.lvalue = false
(1) expression1.lvalue = false //no se permite en el enunciado
(2) expression1.lvalue = expression2.lvalue
(3) expression1.lvalue = true //lo pone en el enunciado

Versión a mano:

Solución: Versión a mano:

4. ¿Cuál es el tipo Java de esta tabla de símbolos?

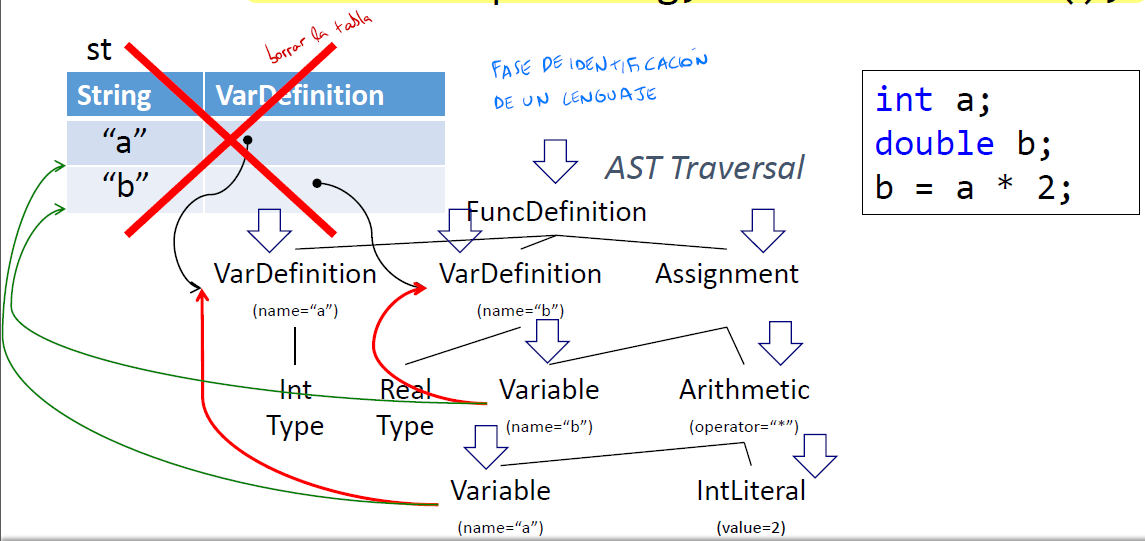
5. Dada la siguiente CFG, definir una gramática atribuida para realizar la fase de Identificación. Nota, se puede usar el objeto st del ejercicio anterior. Una vez que se ha definido la AG, impleméntelo en Java utilizando el patrón de diseño Visitor. (G): Solución: (A): |Atributo|Afecta a|Dominio| |—|—|—| |definition|variable|VarDefinition|

(R):

Nota: las que no se incluyen es porque no requieren nada
(2) IF (!st.put(ID, definition)) print("Variable duplicada")
(7) IF (!st.get(ID)) ERROR("Variable no definida");
	expression.definicion = st.get(ID) //else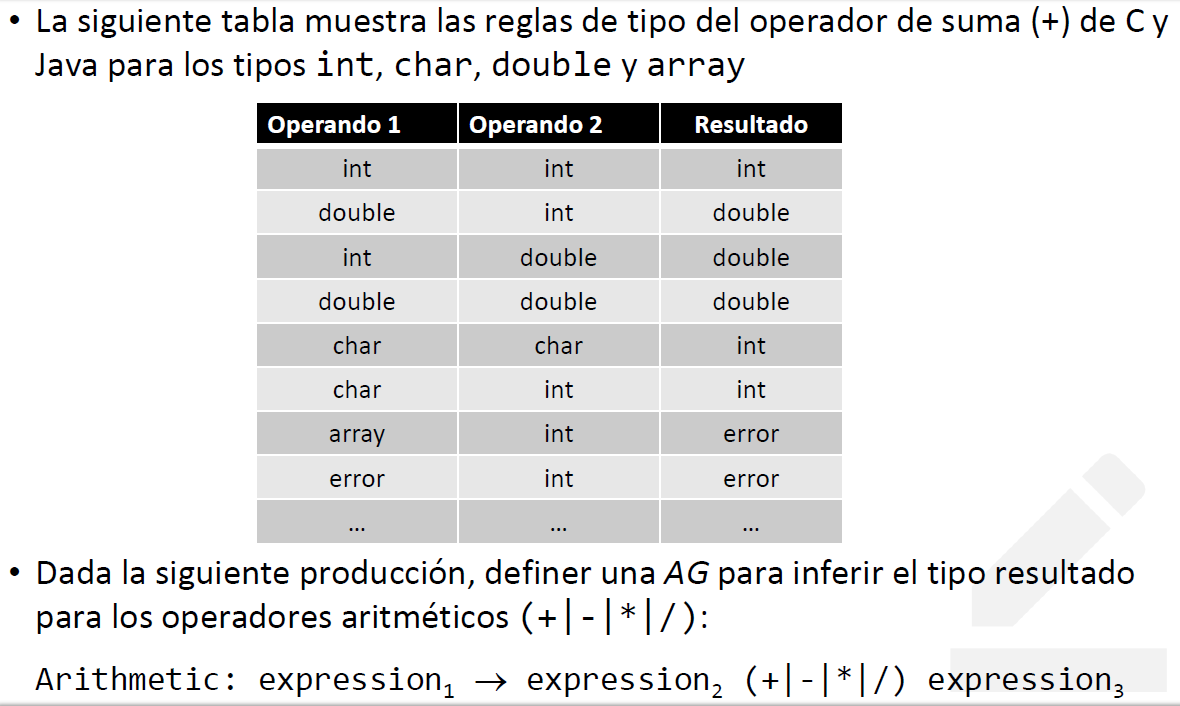

(G): (A):

Atributo	Afecta a	Dominio
type	expression	{int, double, char, error, array}
(R):

//Buena solución: NO USAR INSTANCEOF PARA CADA TIPO
//Usamos el patrón Composite para el tratamiento uniforme de objetos simples y compuestos
(1) expression.type -> expression2.type.arithmetic(expression3.type)

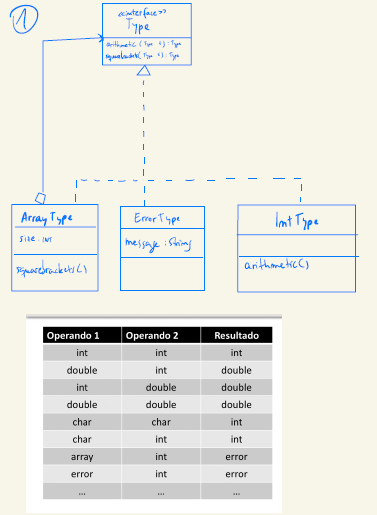
8. (G): (A):

Atributo	Afecta a	Dominio
returnType	statement	type
(R):

(1) statement* -> foreach(statement -> statement.returnType = definition.type.returnType)
(2) expression.mustPromoteTo(statement.returnType)//comprueba si un entero se puede convertir a un double (si promociona)

9. Comprobar que las funciones tengan return en la siguiente gramática. Crear la AG correspondiente:

Nota: falta poner que los dos atributos añadidos tienen dominio booleano

---

Generación de código

1. Nota: un entero ocupa 2 bytes

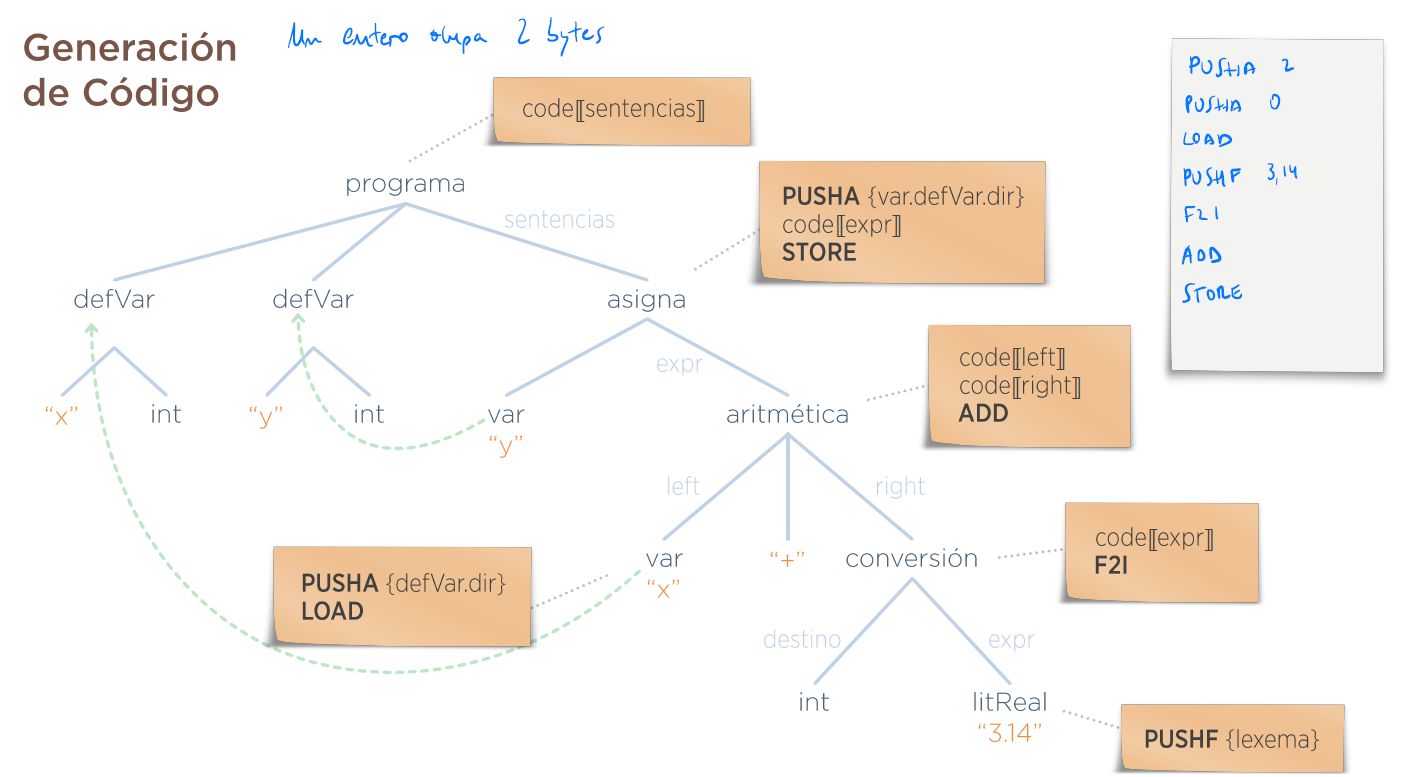
2. Dado el siguiente programa de alto nivel:

a = 3;
b = a;

Escribir el código destino MAPL. Suponer que:

• Las direcciones de memoria de a y b son 0 y 2
• Ambas son variables enteras

Solución:

PUSHA 0 //meto una direccion
PUSHI 3 //meto un 3 ocupando 2 bytes
STOREI //escribo un 3 ocupando 2 porciones de memoria
PUSHA 2
PUSHA 0
LOADI //va a la dirección 0 y lo deja en el tope de la pila
STOREI

//read myInteger;
pusha 0
ini
storei
 
//real = myInteger * 3.4 -7;
pusha 2
pusha 0
loadi
i2f
pushf 3.4
mulf
pushi 7
i2f
subf
storef
 
//write real;
pusha 2
loadf
outf

4. (CREO QUE NO ESTÁ BIEN)

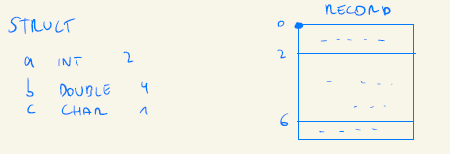
5. EJ TIPICO EXAMEN Solución:

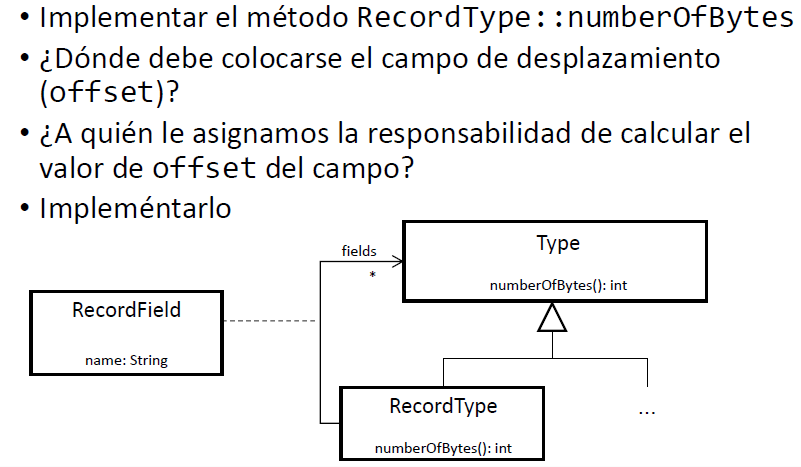
6. Añadir un nuevo método getNumberOfBytes():int a todos los tipos

7. Hay dos estrategias para calcular los desplazamientos de los campos de registro:

   1. Iterando el nodo principal a través de los nodos secundarios de RecordField
   2. En los nodos secundarios RecordField, modificando una variable global declarada como un campo en el Visitor 1 para campos y 2 para variables globales (R):

(8) int byteFilesSum = 0;
	for(RecordField field ; fieldSum){
		field.offset = bytes.byteFilesSum += field.type.getNumberOfBytes();
	}

3. Desplazamiento de las variables globales: (R):

vardefinition.offset = bytesGlobalSum;
bytesGlobalSum += type.numberOfBytes;

4. Implementación es trivial ---FIN EJERCICIO---

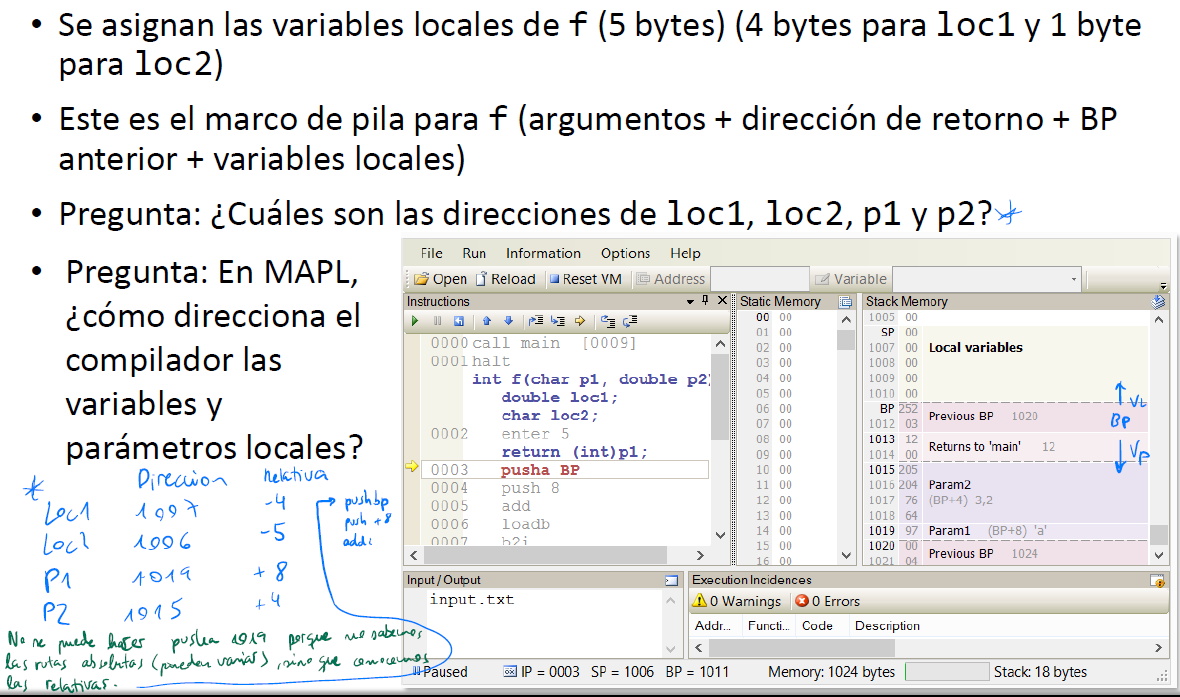
(R):

(1) int LocalBytesSum = 0;
	for(VarDefinition vardef : vardefinition*){
		localBytesSum += varedf.type.getNumberOfBytes();
		vardef.offset = -localBytesSum
	}
(3) int paramBytesSum = 0;
	for(int i = vardefinition*.length() - 1; i--){
		vardf.offset = 4 + paramBytesSum;
		paramBytesSym += vardef.type.number();
	}

8. AGs para Generación de Código (G): (A): code (R):

(1) expression.code = "PUSHB" + (int)CHAR_CONSTANT + "\n" 
(2) expression.code = "PUSHI" + INT_CONSTANT + "\n"
(3) expression.code = "PUSHF" + REAL_CONSTANT + "\n"
(4) if (expression.definition.scope == 0)
		expression.code = "PUSHA" + expression.definition.offset + "\n"
	else
		expression.code = "PUSHBP \n" + "PUSHI" + expression.definition.offset + "\n" + "ADDI \n";
	expression.code += "LOAD" + expression.type.getSuffix() + "\n";
(5) expression1.code = expression2.code + expression2.type.convertTo(expression1.type) + expression3.code + expression3.type.convertTo(expression1.type);
	expression1.code += getOperator(expression1.operator);
	expression1.code += expression1.type.suffix() + "\n"

9. Ejercicio de contexto: (G): (A): code y pushValue (R):

(1) expression1.pushValue = false;
	expression2.pushValue = true;
	statement.code = expression1.code + expression2.code + "STOREI \n"
(2) expression.code = "PUSHA" + expression.definition.offset + "\n"
	if(expression.pushValue)
		expression.code += "LOADI \n"

Solución:

Solucion:

13. Hacer la plantilla de código execute de una sentencia while Solución:

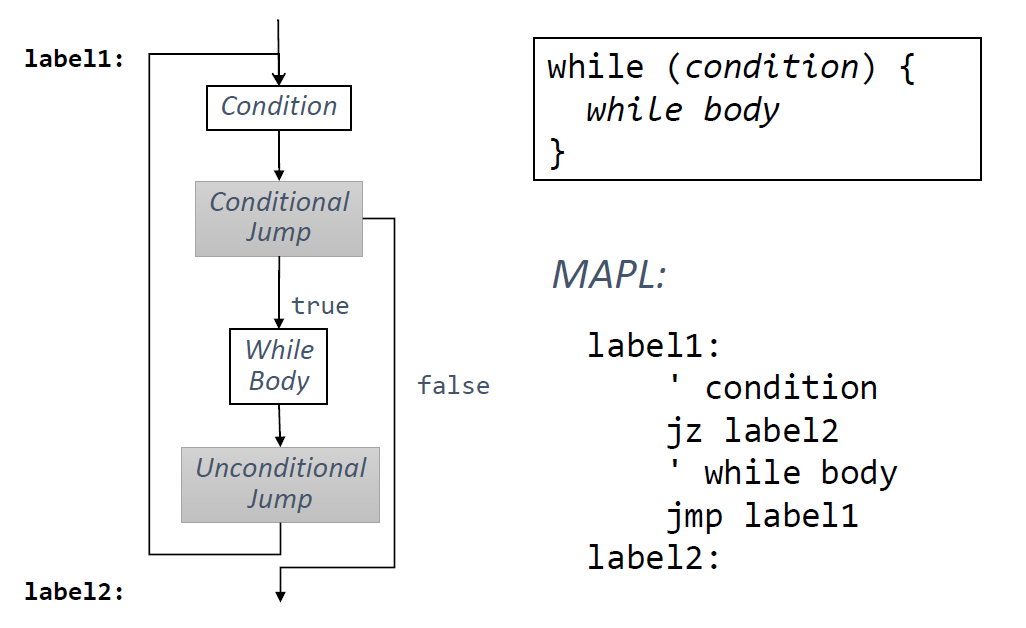
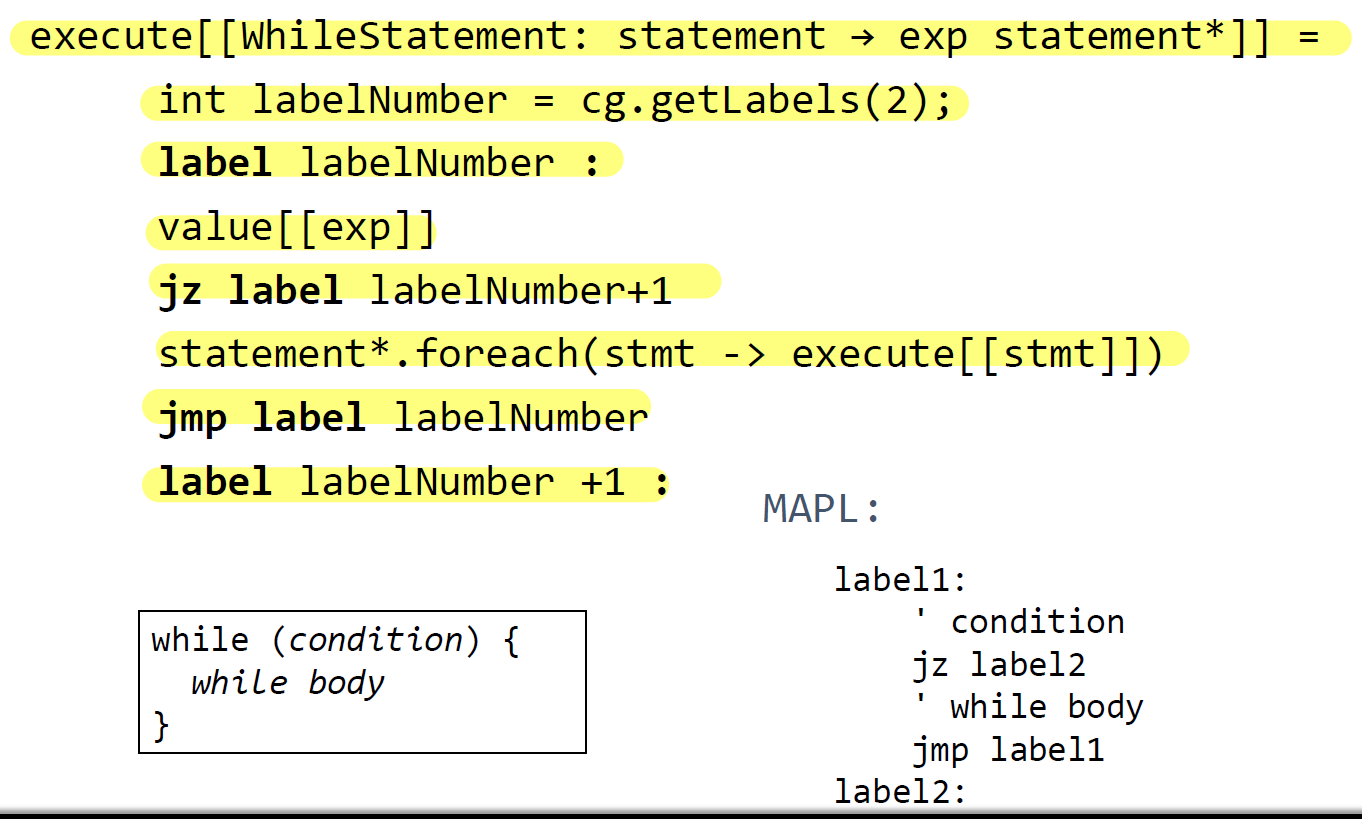
14. Hacer la plantilla de código execute para una sentencia do/while

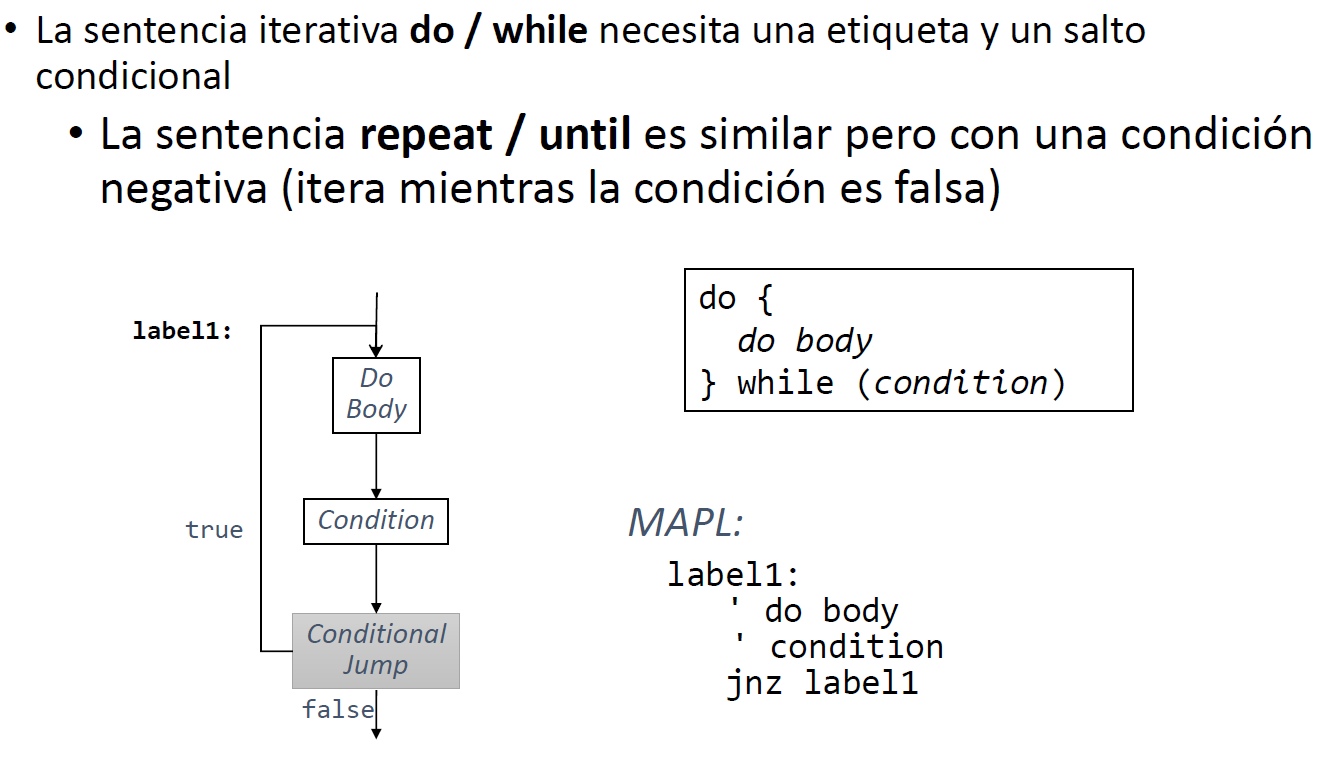
15. Especificar la plantilla de código execute para el bucle for