22 Marzo 2022 💈
Programación dinámica
- Tenemos un array donde guardamos resultados intermedios para calcular el resultado final.
- Es un método iterativo, cuyo origen es una función recursiva. Sustituimos las llamadas recursiva por accesos a las posiciones del array.
- Se repiten operaciones, por tanto se guardan las calculadas en un array para no recalcularlas varias veces.
Problema del cambio
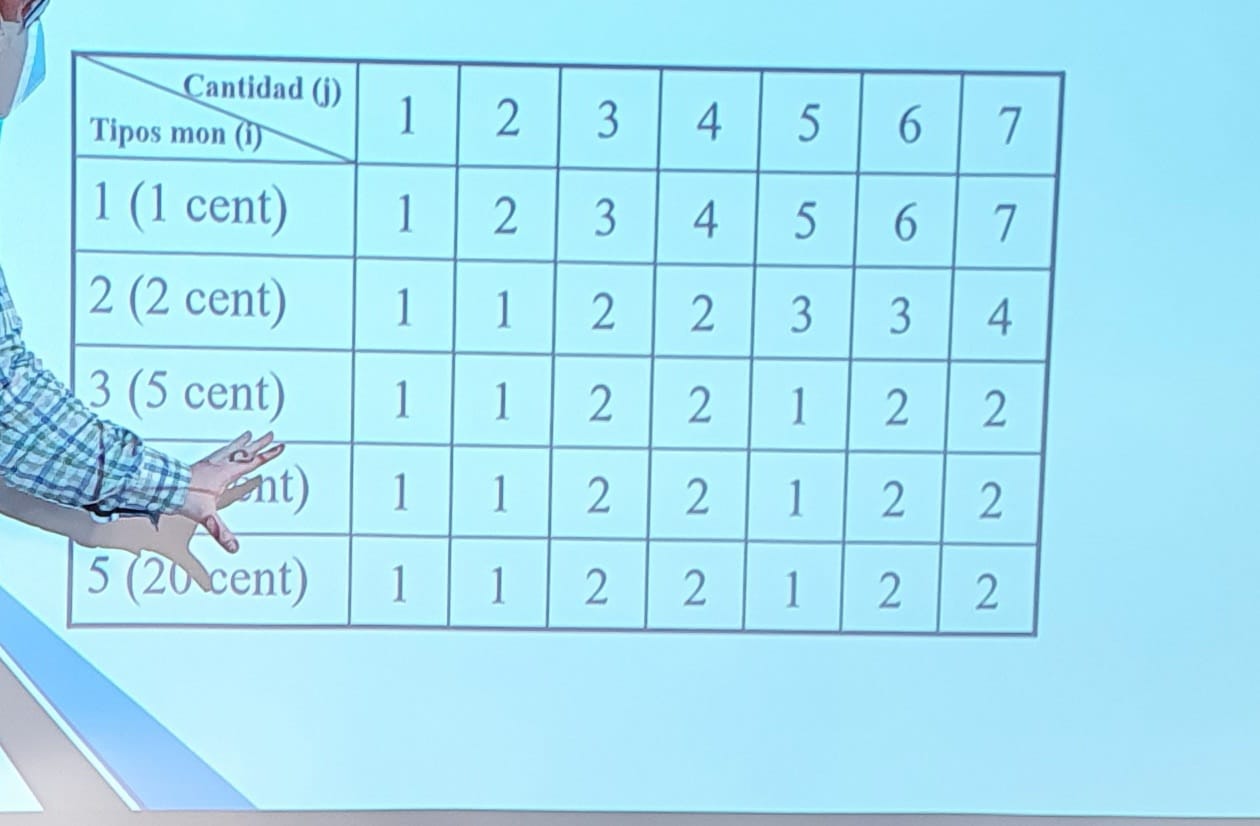Lo que no se ve son 10 céntimos :-)
- Buscar el mínimo para no pasarse, usando la moneda de la iteración o de iteraciones anteriores.
Backtracking
- Problema de las 8 reinas: colocar 8 reinas en un tablero sin que se coman.
- Backtracking explora el grafo, va desarrollando estados hasta que encuentra una solución. Es un algoritmo de fuerza bruta, puesto que lo que hace es desarrollar estados de forma rápida hasta encontrar una solución.
- Técnica ineficiente, con complejidades exponenciales.
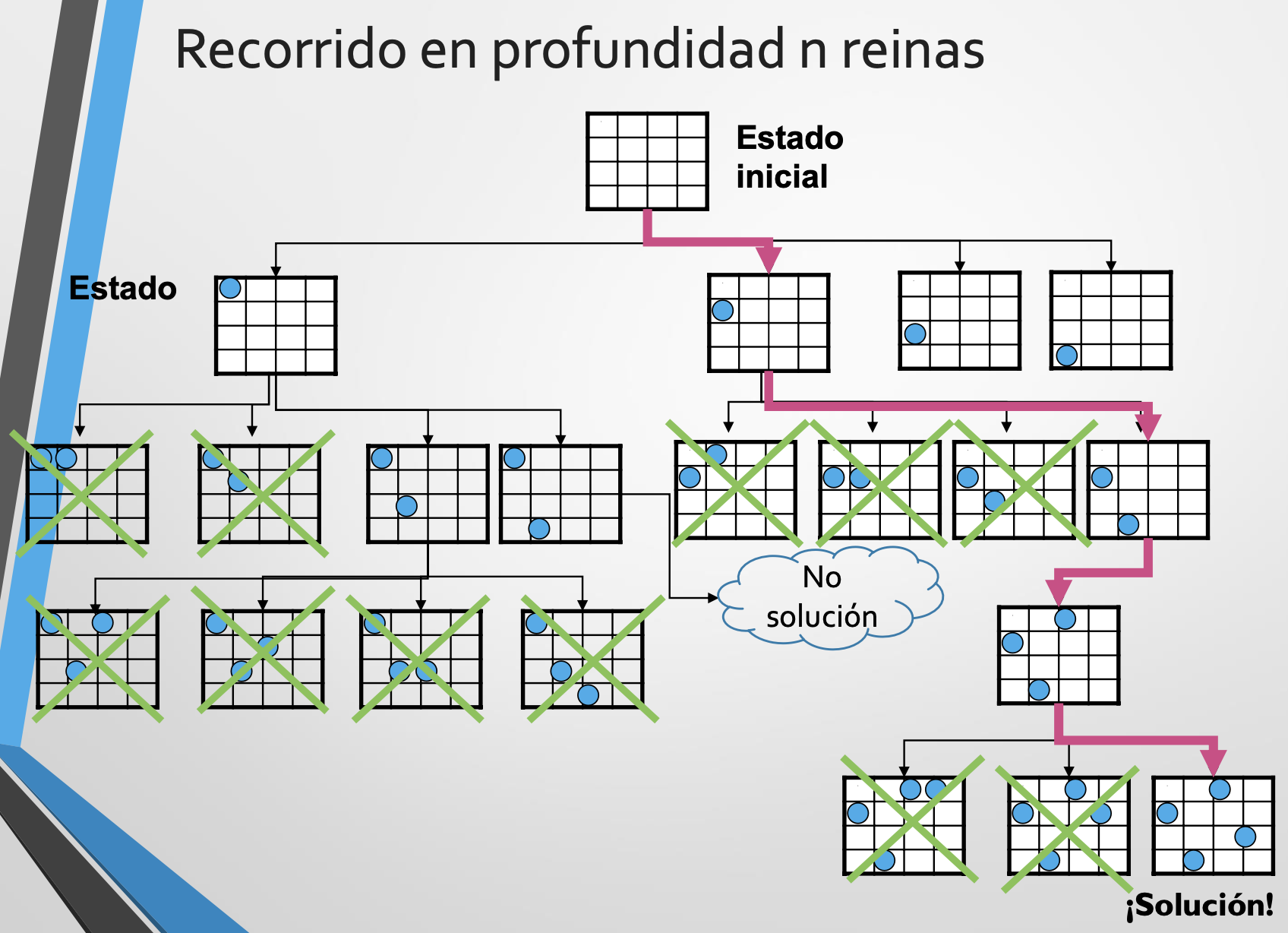
- Grafo implícito: grafo que se desarrolla a medida que se va recorriendo. Ahorra tiempo de ejecución y espacio en memoria.
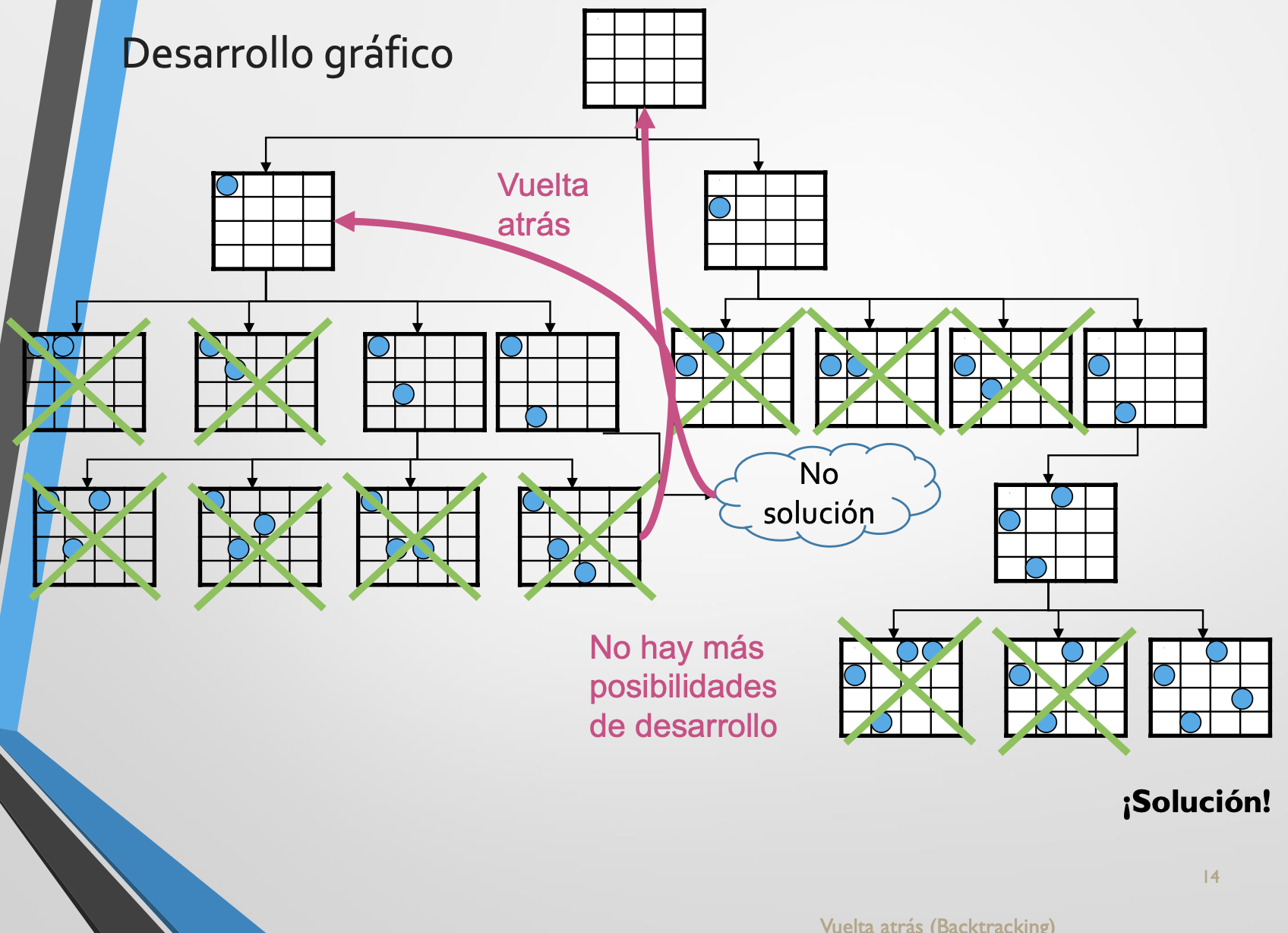
Esquema Backtracking
public static void backtracking(Estado e) {
if (e.esSolucion()) { System.out.println(e); haySolucion= true;
}
else {
Estado estadoHijo= null;
while(e.hasNextHijos() && !haySolucion) {
// siguiente estado hijo válido
estadoHijo= e.nextHijo();
if (estadoHijo!=null) // puede que no queden hijos válidos backtracking(estadoHijo);
}
} }29 Marzo 2022 🗿
- Backtracking busca todas las soluciones posibles.
- También se puede buscar la solución óptima.
Poda de nodos
- Consiste en establecer una condición que impida seguir desarrollando nodos aunque sean válidos.
- Se aplica cuando tenemos que buscar una solución óptima.
- Backtracking tiene complejidad explonencial.
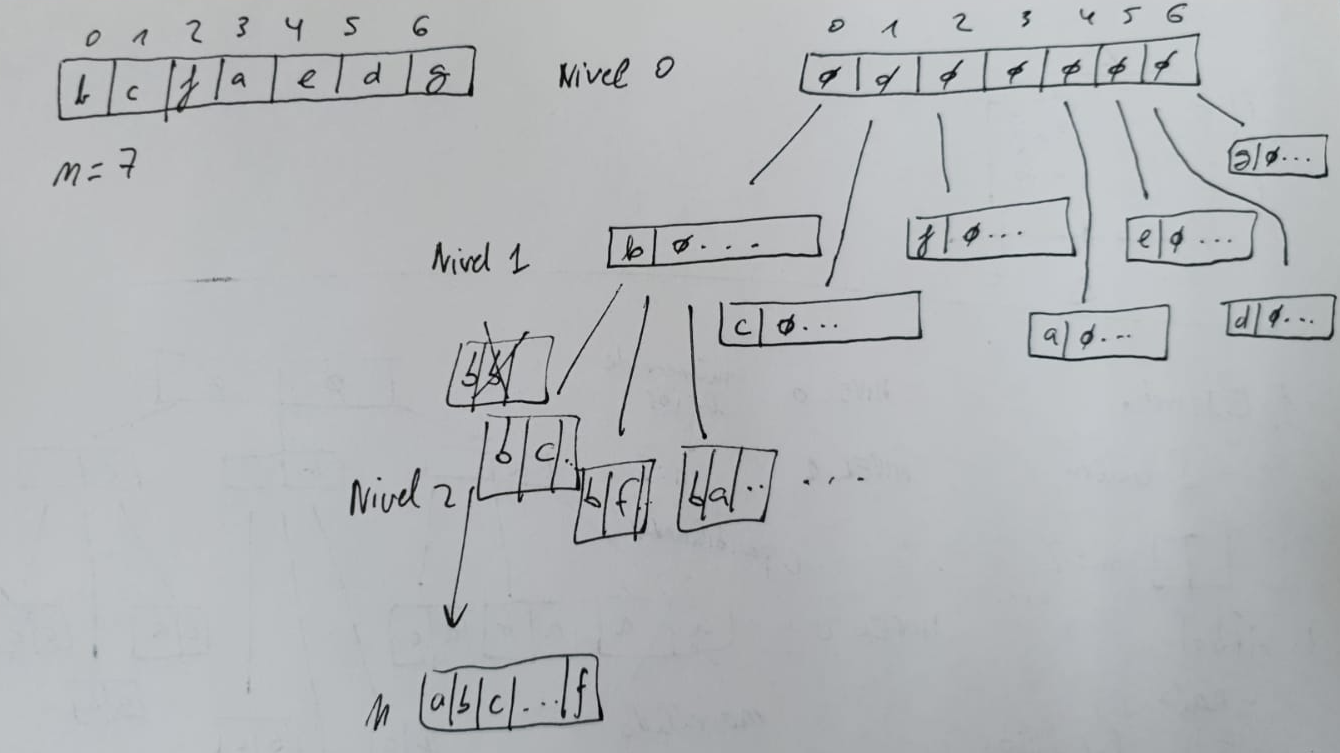
Ejercicio formar palabras a partir de un conjunto de letras
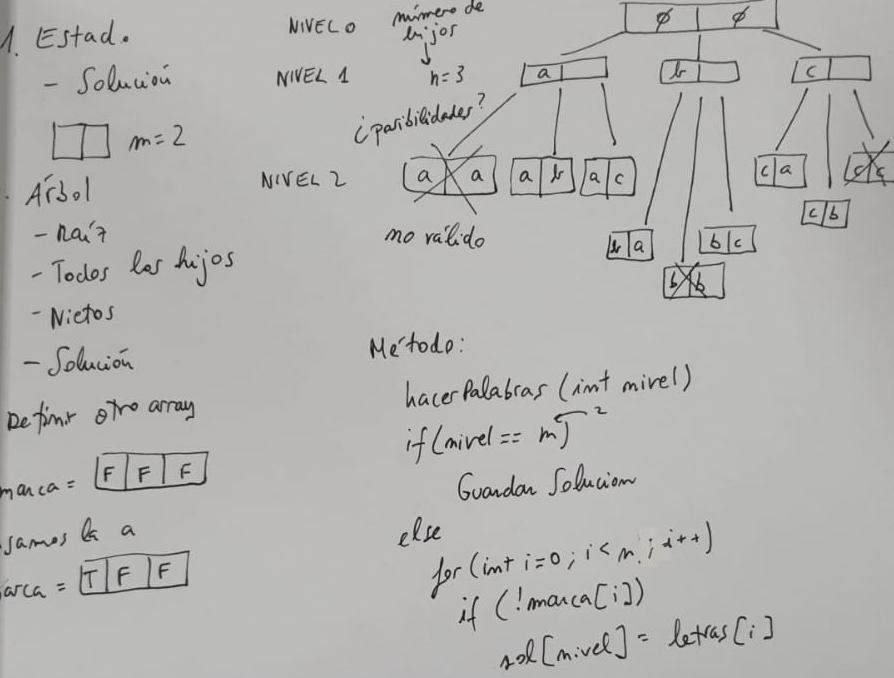
public static void backtracking (int nivel) {
if (nivel==m) //hay ya una palabra completa {
mostrarSolucion();
cont++;
}
else {
for (int i=0;i<n;i++){
if (!marca[i]) {
sol[nivel] =vLetras[i];
marca[i]=true;
backtracking(nivel+1);
marca[i]=false;
}
}
}
}Problema de la asignación de tareas a agentes
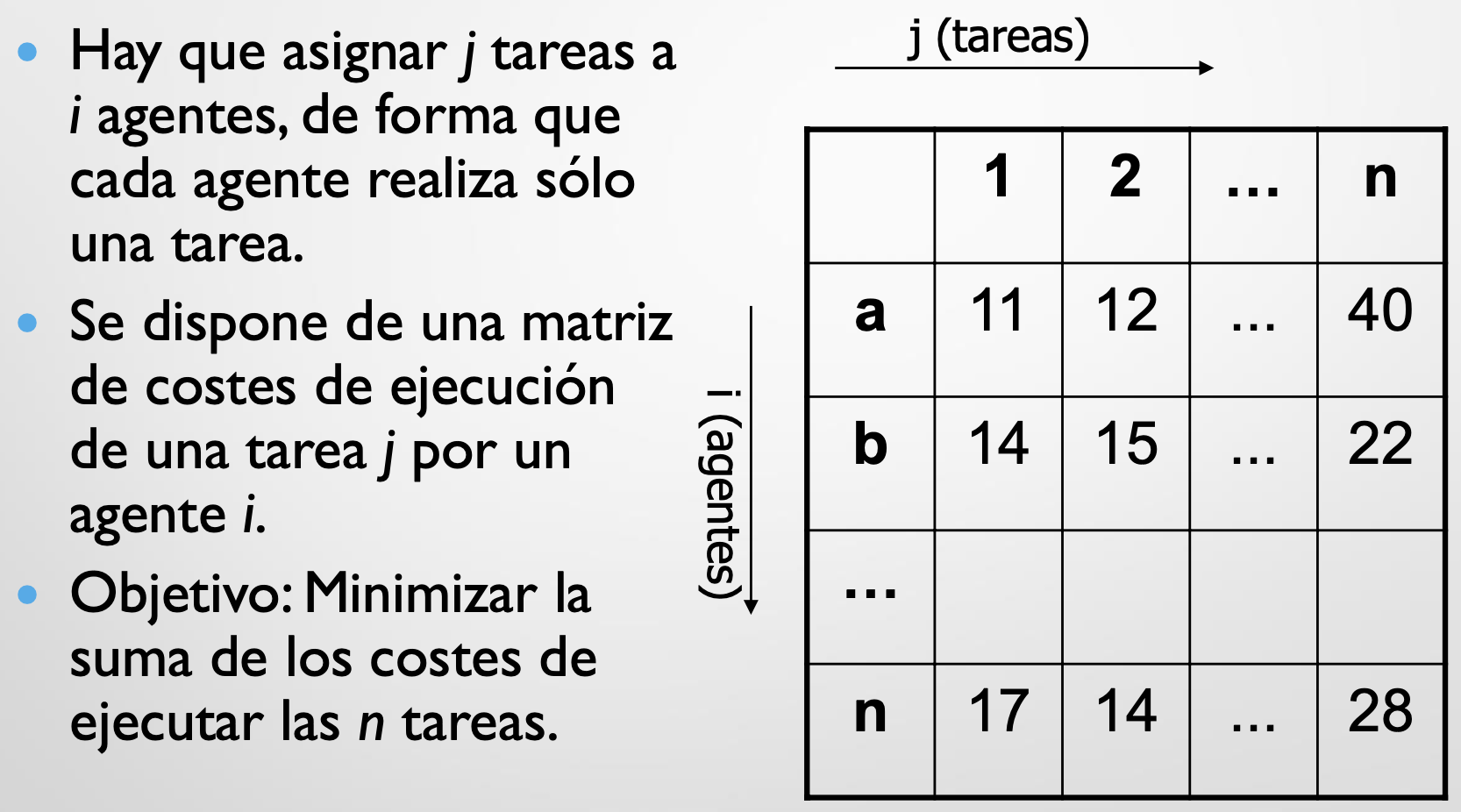
static void backtracking (int nivel) {
if (nivel==n) { //hay ya una asignación completa
if (coste<costeMejor) {
for (int k=0;k<n;k++){
asigMejor[k]=asig[k];
costeMejor=coste;
}
} }
else {
for (int i=0;i<n;i++){
if (!marca[i] && coste<costeMejor ) //ostemMejor->poda
asig[nivel]=i;
coste=coste+w[nivel][i];
marca[i]=true;
backtracking(nivel+1);
coste=coste-w[nivel][i];
marca[i]=false;
}
}
}- Se podría hacer una poda (costemejor).
5 Abril 2022 🔵
- Aplicamos la poda en los problemas de optimización.
Problema del salto del caballo
static void backtracking (int salto,int x,int y) {
if (salto==n*n+1) { // ya acabó de recorrer tablero
seEncontro=true;
mostrarSolucion(); }
else
for (int k=0;k<=7;k++) {
int u=x+h[k]; // nueva posición
int v=y+v[k];
if (!seEncontro &&
u>=0 && u<=n-1 && v>=0 && v<=n-1 && // dentro tablero
tab[u][v]==0) { // casilla no utilizada
tab[u][v]=salto;
backtracking (salto+1,u,v);
tab[u][v]=0;
}
} }
Tema 7, Ramificación y poda 🔊
- No hace falta tener una asignación secuencial.
- Backtracking es recursivo, mientras que poda es iterativo.
public void realizarAnchura(Estado e) {
Cola cola= new Cola(); // Cola FIFO (1o en entrar --> 1o en salir)
boolean haySolucion= false; // Para buscar la primera solución Estado actual;
Estado actual;
cola.insertar(e); // mete estado e en la cola
while (!cola.esVacia() && !haySolucion) {
actual= cola.extraer();
// Examinar todos los hijos del estado actual
for (Estado estadoHijo : actual.expandir()) {
if (estadoHijo.esSolucion())
haySolucion= true;
else
cola.insertar(estadoHijo);
}
} }Diferencias de poda con backtracking:
- Desarrollo de los nodos en anchura.
- Aplicamos heuristico para seleccionar cuál de ellos vamos a desarrollar.
MALA FORMA, sirve para hallar una solución. Para hallar la solución óptima es malo.
19 Abril 2022 ⏰
- El heurístico de ramificación permite saber los nodos que llevan a la solución final
- El heurístico de poda permite ir eliminando aquellos nodos que superen la cota.
