Conceptos básicos
Fases de un traductor
- Si se clasifican por su función se dividen en: Fases de análisis y Síntesis
- Si se clasifican por su dependencia de la máquina destino, se dividen en Front-end y Back-end
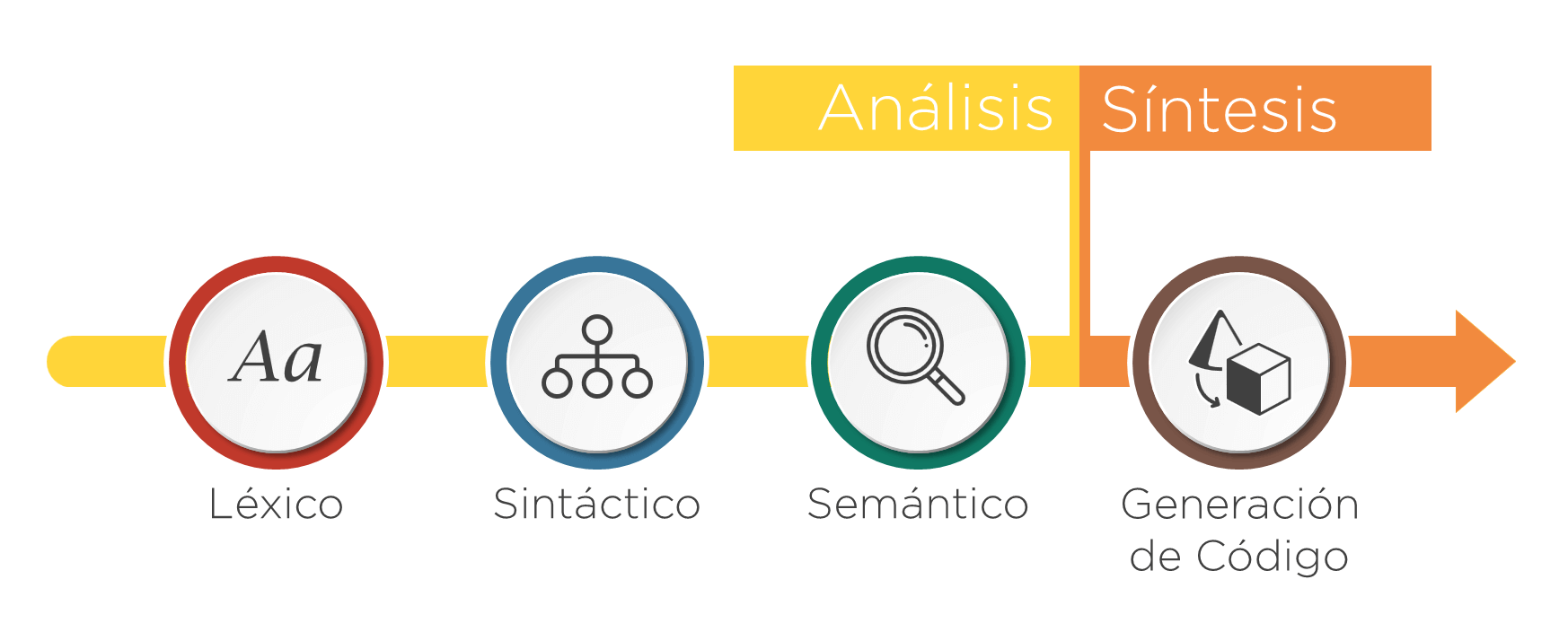
Fases de análisis y Síntesis
-
Las fases de análisis tienen el objetivo de comprobar la validez de la entrada, y en caso positivo identificar su estructura. Las fases de análisis son:
- Análisis Léxico
- Análisis Sintáctico
- Análisis Semántico
-
Las fases de Síntesis son las que dada una entrada válida, se encargan de generar el código de salida. Las fases de síntesis son:
- Generación de código
- Optimización
-
Léxico: separa en tokens
- Comprueba que las palabras sean válidas
- Se asigna a cada lexema un token único
pri**#**nt ; a- Sintáctico: crea el AST
- Forma estructuras a partir de tokens
- Comprueba que las palabras estén en el orden adecuado
- Encuentra estructuras mayores (árbol AST)
print **; a**- Semántico: comprueba que la sentencia se pueda realizar. Tiene dos fases:
- Identificación: busca las definiciones
- Comprobación de tipos: valida el AST con predicados, atributos y funciones semánticas
- Generación de código: dos fases:
- Gestión de memoria: asigna direcciones
- Selección de instrucciones: genera código usando plantillas
Árbol Abstracto (AST)
- Es el árbol mínimo que preserva la semántica de la entrada.
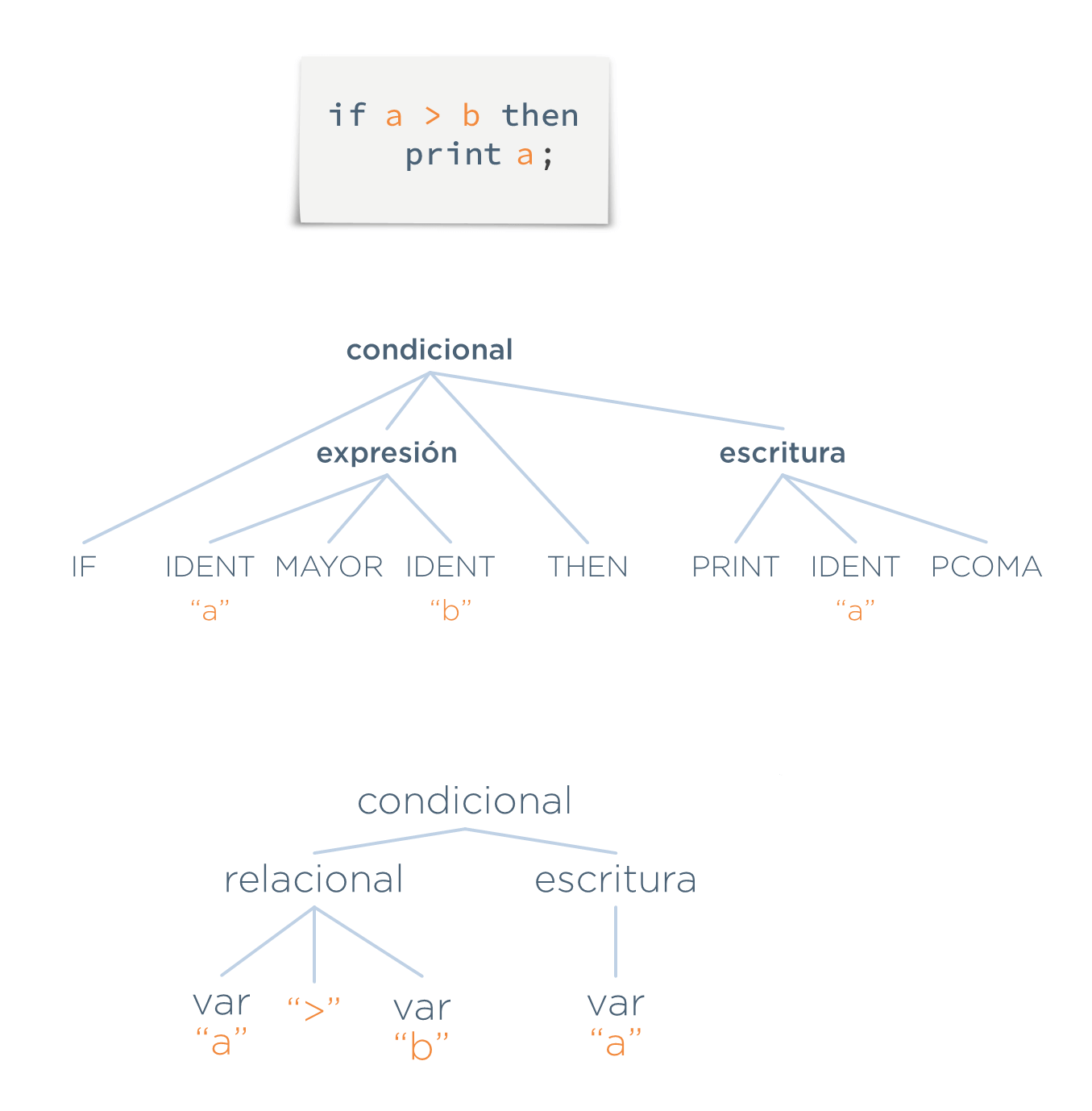
- Para decidir qué debería haber en el AST de un lenguaje, hay que decidir qué es lo mínimo que necesitarían saber las siguientes fases para generar el código destino. Ejemplo: El de abajo sería el AST y el del medio un árbol concreto.
Léxico
- Comprueba que todo lo que se ha escrito en la entrada sean secuencias de caracteres válidas.
- Va leyendo de la entrada carácter a carácter hasta que detecta una cadena válida (lexema) o una cadena errónea.
- Una vez encontrado un lexema, le asigna un número llamado Token (al cual se le puede ver como el tipo o la categoría a la que pertenece el lexema)
- Entran caracteres y salen tuplas
- Las tuplas son una clase de token (conjunto de lexema + token)
- Cuando no hay más tokens, se llama a una convención END (EOF) = 0
El léxico facilita las fases posteriores creando tokens que representan dichas palabras reservadas.

Dado que sería engorroso trabajar con números, se definen constantes para simplificar su manejo:

Ejemplo de analizador léxico:
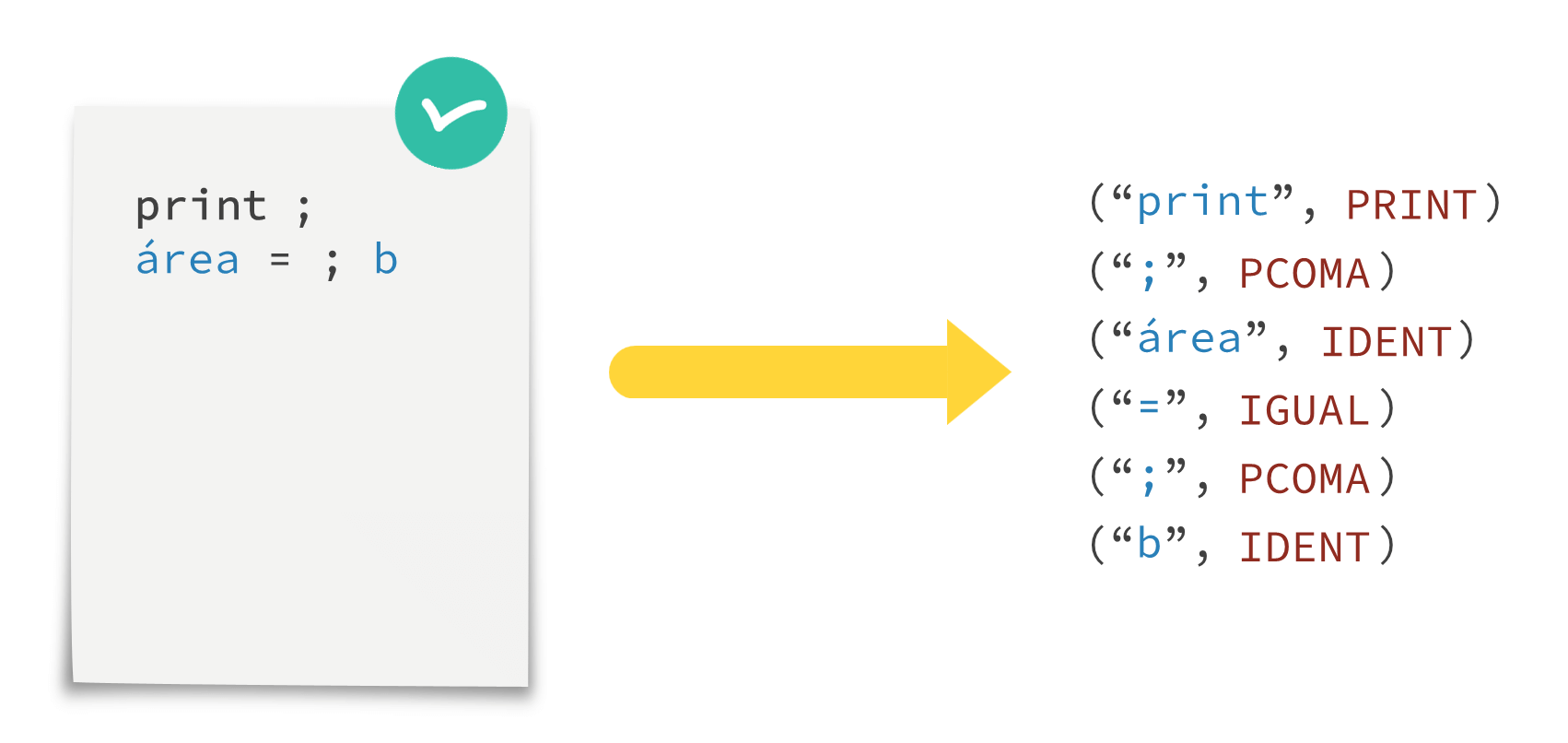
Qué no hace el léxico
- No se ocupa de que las cadenas aparezcan en el orden adecuado (eso lo hace el sintáctico)
altura = ; 25 // Esto no es problema del léxico!!Representación de los tokens
- Los tokens se definen como constantes
- Sin embargo, si el token está formado por un sólo lexema y dicho lexema tiene sólo un caracter, se le asocia como número el token de código ASCII
static final int WHILE = 257;
static final int IF = 260;
...
static final int IGUAL = ‘=’;
static final int P_COMA = ‘;’;Esto permite hacer una simplificación de código, ya que es un número conocido y no es necesario definir dichas constantes por ser redundante:
static final int IDENT = 256;
static final int WHILE = 257;
static final int IF = 260;
...
// static final int IGUAL = ‘=’;
// static final int P_COMA = ‘;’;Implementación de un token
public class Token {
public Token(String lexeme, int tokenType, int line, int column) {
this.lexeme = lexeme;
this.tokenType = tokenType;
this.line = line;
this.column = column;
}
public String getLexeme() { return lexeme; }
public int getType() { return tokenType; }
public int getLine() { return line; }
public int getColumn() { return column; }
private String lexeme;
private int tokenType, line, column;
}¿Cómo hacer una especificación? Pasos
Expresiones regulares
- Determinar los tokens: hay que definir de una forma lo más clara posible lo que representa un token En definitiva, la solución correcta para los delimitadores es hacer un token por cada uno:
class Lexico {
static final int IDENT = 256;
static final int WHILE = 257;
...
//no hacer static final int DELIMITADOR = 261; // Lexemas: '(' ')' '{' '}'
static final int PARENT_A = ‘(’;
static final int PARENT_C = ‘)’;
static final int LLAVE_A = ‘{’;
static final int LLAVE_C = ‘}’;
}- Definir un patrón para cada token: hay que decidir qué es válido y qué no.
_a
hol#a
_32
¿Són lexemas válidos? ¿Són identificadores (IDENT)? → depende de las decisiones de diseño tomadas en los metalenguajes
Metalenguajes
- Un metalenguaje es un lenguaje que se caracteriza porque aquello que describe es otro lenguaje. Necesitan dos propiedades:
- Precisión: ante cualquier entrada no haya duda de si es válida o no para ese token
- Concisión: que la regla sea lo más compacta posible para facilitar su entendimiento e implementación Sin embargo, no hay un metalenguaje que sirva para todo. Hay que usar distintos metalenguajes para definir mejor cada aspecto por separado. Los dos metalenguajes más usados son Autómatas finitos y expresiones regulares
Expresiones regulares. Operadores

Ejemplo:
pa+ // pa paa paaa paaaa paaaaa...
(pa)+ // pa papa papapa papapapa...Tareas de un léxico
En cada llamada al método nextToken()
- Ignorar los comentarios
- Ignorar los espacios en blanco y los saltos de línea
- Comprobar los patrones de la especificación
- Notificar errores
Implementación (que puede ser manual o con herramienta)
- Ignorar comentarios y token comentario
- Comprobar patrones
- Notificar error (no hay token error)
Notación de ANTLR. Aspectos generales
Operadores
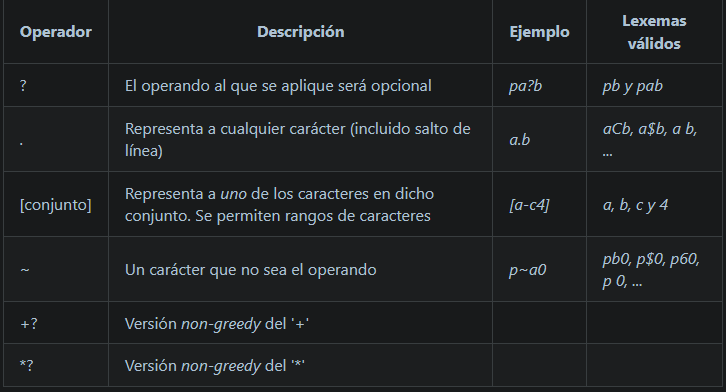
La versión normal (greedy) y la versión non-greedy se diferencian en el momento en el que paran de reconocer una cadena. La versión non-greedy dejar de reconocer en cuanto ha encontrado un lexema válido. La versión normal (o greedy) sigue reconociendo por si puede formar un lexema más largo que también cumpla el patrón (si no lo consigue, devolvería lo mismo que la versión non-greedy). Es decir, la versión normal intenta formar el lexema más largo que cumpla el patrón.
Por ejemplo, supóngase el siguiente patrón con la versión normal del ’*‘:
T: '@' .* '@';Ante una entrada como la siguiente:
@hola@@adios@
Sin embargo, usando la versión non-greedy del operador:
T: '@' .*? '@';En la primera llamada a nextToken se formaría sólo el lexema “@hola@” (deja de leer más caracteres en cuanto la entrada cumple el patrón) y en una segunda llamada a nextToken ya se devolvería “@adios@“.
Prioridades de las reglas
¿Qué pasa si una misma entrada casa con más de un patrón? Hay que conocer las reglas de prioridad de ANTLR.
Supóngase la situación con el fichero de ANTLR de la izquierda y la entrada “32954”.

Cumpliendo esas reglas, se podría reconocer esa entrada de las tres formas que se muestra en la imagen: la primera devolvería dos lexemas, la segunda tres y la última sólo uno. ¿Cuál de ellas produce el método nextToken generado por ANTLR?
- NORMA1: Cuando una entrada puede ser reconocida por más de una regla, se elige aquella que forme el lexema más largo
- ANTLR elegiría la regla T2 ya que forma el lexema “32954” que es más largo que el lexema “32” que formaría T1.

Supóngase ahora la siguiente situación en la que se cambia la cadena de entrada y pasa a ser “32ALJ”.

En este caso ambas reglas forman un lexema del mismo tamaño, por lo que la norma 1 no es de ayuda.
- NORMA2: Cuando varias reglas forman un lexema del mismo tamaño, se elige la regla que se haya definido primero
- Siguiendo la norma 2, nextToken devolvería ahora el token T1 con el lexema “32”.
Mirar ejercicios en Léxico
Sintáctico
- Se encarga de que los tokens estén en el orden adecuado. Para ello:
- Identifica estructuras
- Construye un árbol
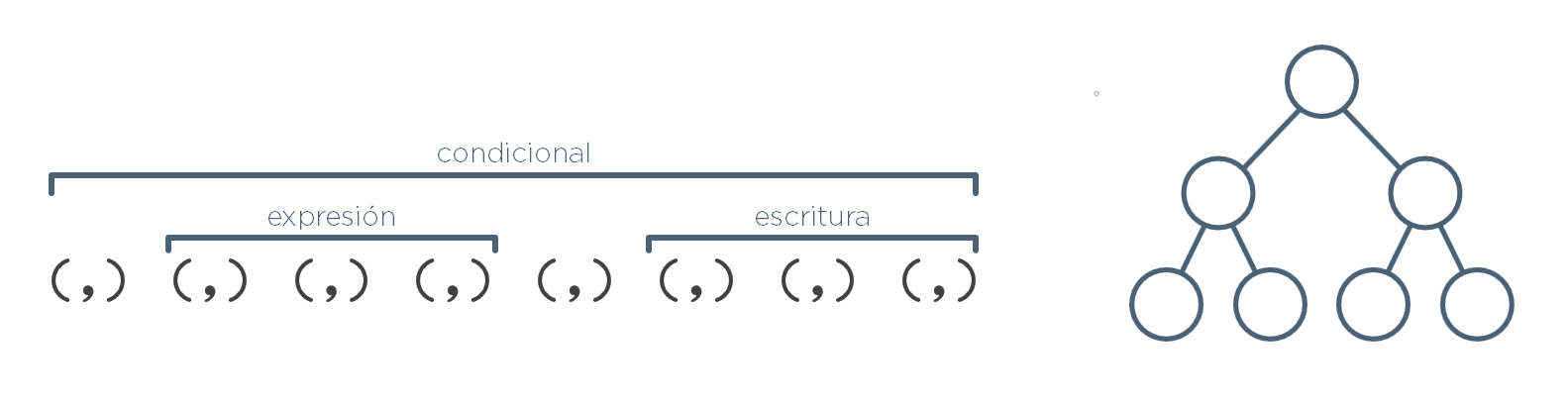
Ejemplo: Supóngase este programa:
if a > b then
print a;Lo que haría el analizador sintáctico, una vez recibidos los tokens, sería encontrar las estructuras resaltadas en negrita encima de los tokens:
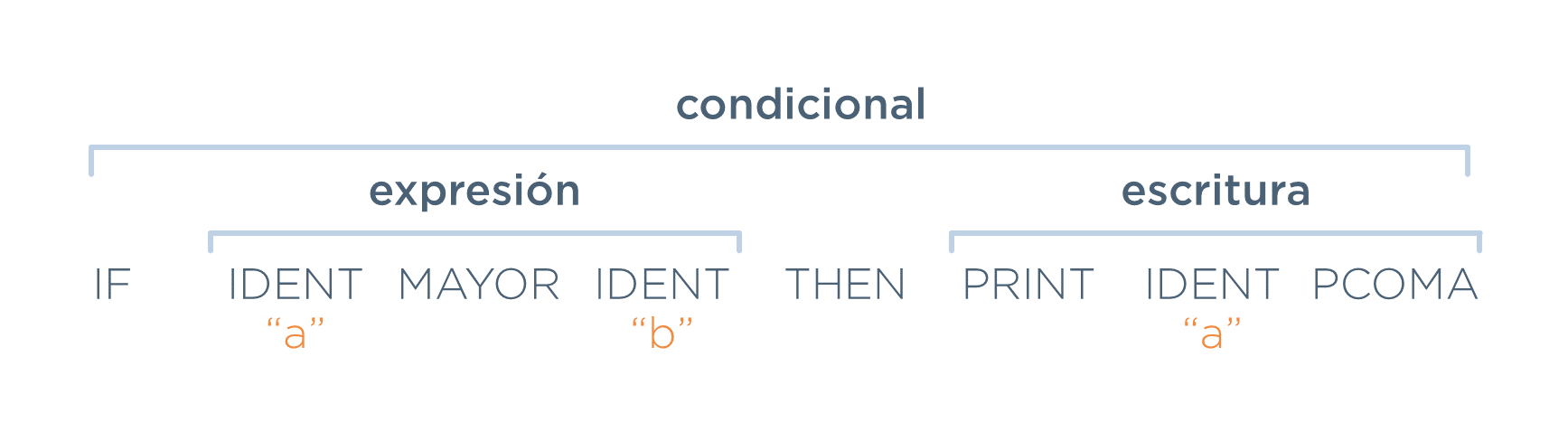
Ahora, el analizador sintáctico forma un árbol que muestra la composición del programa analizado. A este árbol se le denomina árbol de análisis gramatical. En estetexto se le llamará árbol concreto:
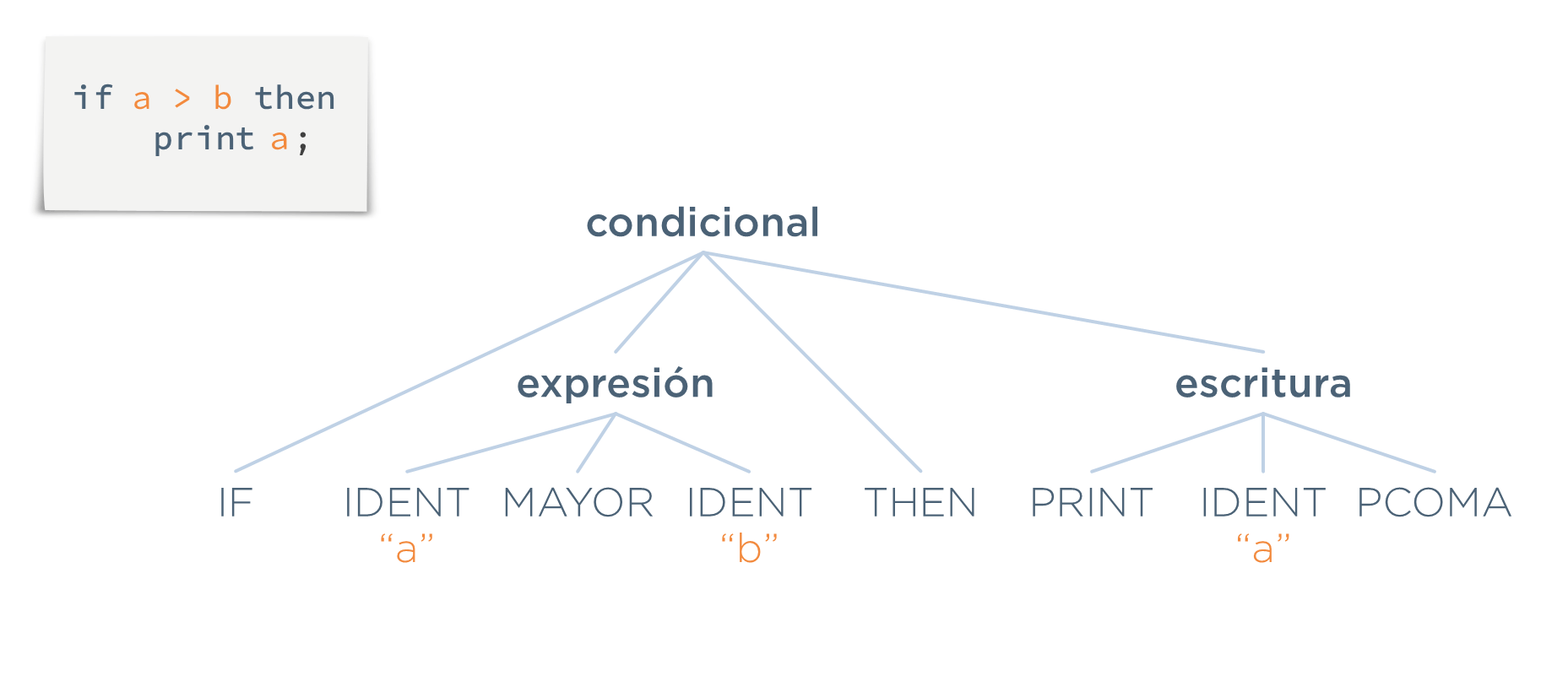
Reglas
Supóngase que se quiere establecer en lenguaje natural las reglas que dicten cómo es una expresión aritmética como la siguiente:
(3 + 4) * 5Las reglas podrían ser:
- Las expresiones usan notación infija
- El número de paréntesis abiertos es siempre mayor o igual al de paréntesis cerrados excepto al final de la expresión, donde tendrán que ser iguales Aunque parecen suficientemente claras, podría plantearse una entrada como la siguiente:
3 (+ 4 *) 5La entrada anterior se pretendía que fuera inválida. Sin embargo, cumple ambas reglas. Por tanto, habría que replantearse las mismas. Por ello, se recurrirá de nuevo a los metalenguajes: lenguajes que nos sirven para definir de forma precisa (sin ambiguedades) y concisa las reglas de un lenguaje. En concreto, los metalenguajes que se usarán en esta fase son las Gramáticas Libres de Contexto (GLC) en notación BNF y EBNF y, cuando se llegue a la construcción del árbol, las Gramáticas Abstractas (GAb).
Gramáticas libres de contexto (GLC)
- Una GLC es un conjunto de 4 elementos:
G = { VT, VN, s, P }
Dichos elementos son:
- VT: es un conjunto de símbolos terminales (tokens del analizador léxico)
- VN: es un conjunto de símbolos no-terminales. Son las estructuras que hay en el lenguaje (que se formarán a partir de símbolos terminales y de otras estructuras)
- s: es un símbolo no-terminal, es el símbolo inicial. Es la estructura superior que incluirá a todas las demás.
- P: es un conjunto de reglas de producción (o producciones) formadas por un símbolo no-terminal en el antecedente (a la izquierda de la flecha) y una secuencia de símbolos (terminales y/o no-terminales) en el consecuente. Las reglas son las que nos dicen cómo se forman los símbolos no terminales de VN a partir de otros símbolos. Un ejemplo de GLC sería la gramática G siguiente:
G = { VT, VN, programa, P }
Donde a continuación se describen cada uno de sus componentes:
VT = { IDENT IF THEN ELSE = ( ) NUM + * }
VN = { programa, instrucciones, instr, expr }
P = {
programa ⟶ instrucciones
instrucciones ⟶ instr
| instrucciones instr
instr ⟶ IDENT = expr
| IDENT ( expr )
| IF expr THEN instr ELSE instr
expr ⟶ NUM
| expr + expr
| expr * expr
}
En el no-terminal instrucciones puede observarse que, dado que las GLC no tienen los operadores de repetición que se vieron en el analizador léxico (’+’ y '*'), la solución equivalente aquí es utilizar la recursividad para indicar repetición de elementos (en concreto, la gramática indica que instrucciones es una secuencia de una o más instr)
Nota: 📌 Se utiliza el separador
|para definir de una forma más compacta varias reglas que compartan el mismo antecedente.
a ⟶ b
| c
Pero lo anterior sigue siendo la definición de dos reglas (no de una), ya que es equivalente a:
a ⟶ b
a ⟶ c
Notación BNF
- Es la notación más común para representar gramáticas libres de contexto. En ella no se definen expresamente cada uno de los elementos de la gramática, sino que sólo se incluyen las reglas de producción y el resto de los conjuntos se deducen de ellas. La gramática anterior en BNF sería:
programa ⟶ instrucciones
instrucciones ⟶ instr
| instrucciones instr
instr ⟶ IDENT '=' expr
| IDENT '(' expr ')'
| IF expr THEN instr ELSE instr
expr ⟶ NUM
| expr '+' expr
| expr '*' expr
De ahí se deducen el resto de los elementos de la GLC:
- VT, los tokens, que son aquellos símbolos que estén en mayúsculas o entrecomillados (IDENT, =, (, ), IF, THEN, ELSE, NUM)
- VN, los no-terminales (estructuras), son todos aquellos símbolos en los antecedentes de las reglas (programa, instrucciones, instr y expr)
- s, el símbolo inicial, será el antecedente de la primera regla (programa)
Notación EBNF
- Es una extensión de la BNF que añade 4 operadores:

La gramática anterior, expresada en EBNF, podría simplificar las dos primeras reglas de la gramática (instr y expr seguirán igual):
programa ⟶ instr+
instr ⟶ IDENT '=' expr
| IDENT '(' expr ')'
| IF expr THEN instr ELSE instr
expr ⟶ NUM
| expr '+' expr
| expr '*' expr
Validación de entradas. Definiciones
Transformación
- Transformación (o paso de derivación): acción de coger uno de los símbolos no-terminales de una cadena y sustituirlo por la parte derecha de una regla que tenga como antecedente a dicho símbolo. Supóngase una gramática G:
s ⟶ a b Z
a ⟶ Y a
a ⟶ X a
a ⟶ ε
b ⟶ ε
b ⟶ W b
Supóngase ahora la cadena X a b Z. Si se toma el símbolo a de dicha cadena y, aplicando la segunda regla a ⟶ Y a, se sustituye dicho símbolo por la parte derecha de la regla, se obtiene la cadena X Y a b Z.
Se dice entonces que la cadena X Y a b Z es una transformación de X a b Z y se expresa con la siguiente notación (nótese que se lee al revés de cómo se escribe):
X a b Z ⟹ X Y a b Z
Nota:📌 Nótese la forma de las dos flecha que han aparecido en este tema:
- Se utiliza
⟶para definir una regla o producción de una gramática.- Se utiliza
⟹indica que a la cadena de su izquierda se le ha aplicado una regla para obtener la cadena de la derecha (que se ha realizado una transformación).
Derivación
- Derivación: es cualquiera de las cadenas que se obtienen a partir de ella aplicando una o más transformaciones (pasos de derivación)
Supóngase una gramática G:
s ⟶ a b Z
a ⟶ Y a
a ⟶ X a
a ⟶ ε
b ⟶ ε
b ⟶ W b
Serían ejemplos de derivaciones de la cadena X a b Z todas las cadenas que están a su derecha en el siguiente ejemplo:
X a b Z ⟹ X Y a b Z ⟹ X Y b Z ⟹ X Y W b Z
Se indica que una cadena es una derivación de otra con el símbolo (que indica que se han producido cero o más transformaciones). Por ejemplo, para indicar que la cadena
X Y W b Z es una derivación de X a b Z se expresa de la siguiente manera (nótese que, de nuevo, se lee al revés de cómo se escribe):
X a b Z
X Y W b Z
De hecho, en el ejemplo anterior, se pueden ver también las siguientes derivaciones de la misma cadena:
X a b Z
X Y a b Z
X a b Z
X Y b Z
Sentencia
- Sentencia: caso particular de derivación.
Nota: Se dice que una cadena
tes una sentencia de la gramática G si cumple dos condiciones: 1. Está formada únicamente por símbolos terminales (en mayúsculas) 2. Es una derivación del símbolo inicial s de la gramática (st).
Como ejemplo, supóngase la gramática G:
s ⟶ a b Z
a ⟶ Y a
a ⟶ X a
a ⟶ ε
b ⟶ ε
b ⟶ W b
Para saber si la cadena X W Z es una sentencia de G, habría que comprobar las dos condiciones anteriores.
- La primera la cumple ya que la cadena esta formada sólo por terminales.
- La segunda la cumple por ser una derivación de
s(es decir, que se puede partir de dicho símbolo y, haciendo transformaciones, se puede llegar a la cadena). Esta sería la secuencia de transformaciones que lo demuestran:
s ⟹ a b Z (por regla 1)
⟹ X a b Z (por regla 3)
⟹ X b Z (por regla 4)
⟹ X W b Z (por regla 6)
⟹ X W Z (por regla 5)
Por tanto, la cadena X W Z es una sentencia de la gramática G.
Lenguaje
- Es el conjunto de todas las sentencias de una gramática, es decir, el conjunto de todos los posibles programas
Es decir, el lenguaje generado por una gramática G es el conjunto de todas las cadenas formadas por terminales a las que se puede llegar a partir del símbolo inicial s.
Supóngase una gramática G:
s ⟶ X a
a ⟶ Y b
a ⟶ ε
b ⟶ W
b ⟶ ε
Su lenguaje L(G) estaría formado por las tres sentencias que se pueden formar:
L(G) = { X, X Y, X Y W }
En este caso, que es una gramática sencilla, ha salido un conjunto finito. Sin embargo, lo habitual en un lenguaje práctico es que sea un conjunto infinito de sentencias.
Gramáticas equivalentes
Supónganse la dos gramáticas G1 y G2 siguientes:
// Gramática G1
s ⟶ s + s
s ⟶ X
// Gramática G2
s ⟶ X mt
mt ⟶ + X mt
mt ⟶ ε
Si se calculan sus respectivos lenguajes, se obtiene lo siguiente:
L(G1) = { X, X + X, X + X + X, X + ... + X }
L(G2) = { X, X + X, X + X + X, X + ... + X }
Por tanto, puede verse que ambas gramáticas, aunque son distintas, generan el mismo lenguaje: una o más X sumadas.
Validez de una entrada
- Recopilando todas las definiciones anteriores, se puede llegar a la conclusión de que una entrada será válida si pertenece al lenguaje que genera la gramática, es decir, si es una sentencia del mismo. Y para averiguar si es una sentencia, vamos comprobando si se puede llegar desde el símbolo inicial s hasta dicha cadena.
Árbol Concreto (o de Análisis Gramatical)
- Árbol que se construye a la vez que se realizan las transformaciones.
Por ejemplo, supóngase la siguiente gramática G:
s ⟶ e
e ⟶ e + e
e ⟶ e * e
e ⟶ LITENT
Supóngase que se quiere saber si la entrada 3 + 4 * 5 es válida según dicha gramática. Para ello, se encuentra la derivación de s que lleva a dicha cadena (a la izquierda de la imagen). Lo que se hace en el árbol de la derecha es ir anotando qué símbolo se ha sustituido por qué otros en cada transformación:
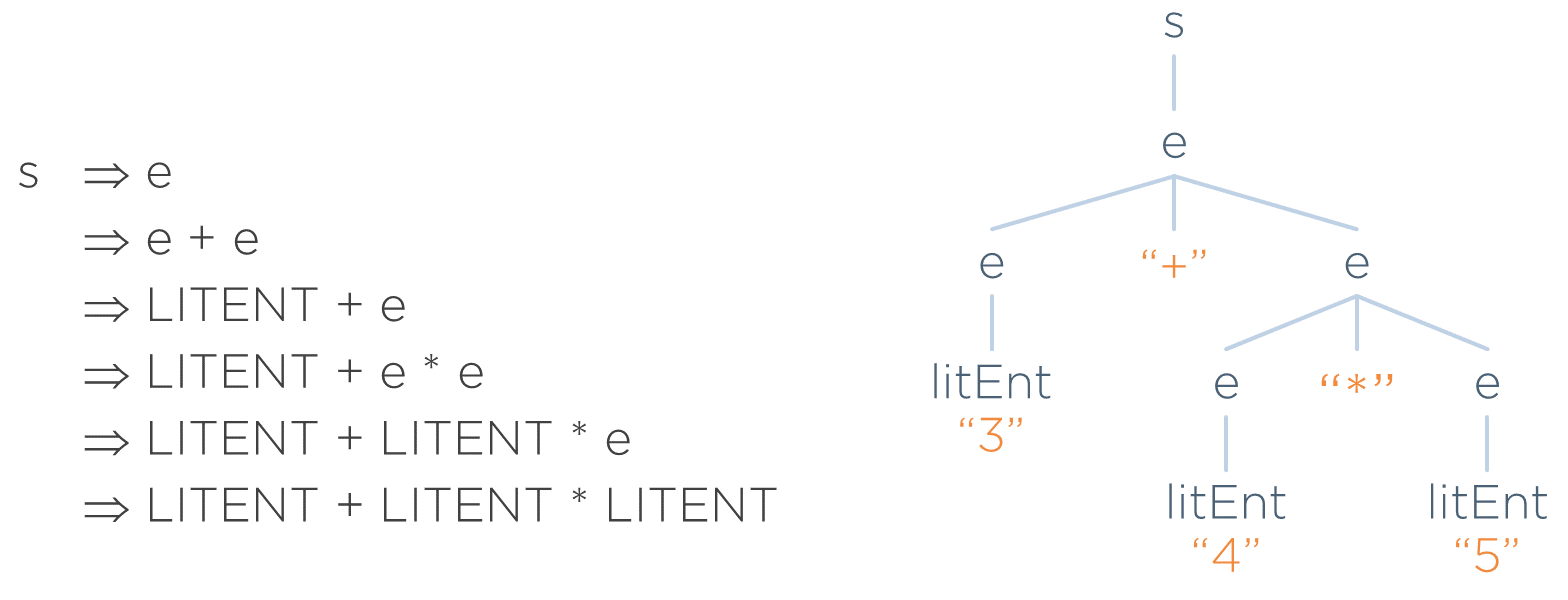
De esta manera, se obtiene el árbol concreto correspondiente a la entrada.
Nótese que en un árbol concreto se cumple que:
- La raíz del árbol será el símbolo raíz de la gramática.
- Todo nodo terminal será un token.
- En todo subárbol formado por un padre y sus hijos:
- El padre será el antecedente de una producción de la gramática.
- Los hijos serán el consecuente de dicha producción.
Parsers
- Algoritmo que recibe unas reglas en forma de gramática que indican qué entradas son válidas y una entrada en forma de tokens, que encuentra la regla adecuada a usar en cada paso para llegar desde el símbolo inicial a dicha entrada (si existe ese camino). Es decir, busca una combinación de transformaciones que lleve del símbolo inicial a la cadena.
- Hay varios algoritmos con distintos grados de compromiso
Características de los parsers
Hay que conocer unos términos que derivan cómo trata un parser las siguientes situaciones:
- En qué dirección realiza el reconocimiento de la cadena de entrada
- Cómo selecciona las reglas a la hora de realizar una transformación
Tipos de algoritmos. Clasificación por dirección y selección de reglas

Dirección de reconocimiento
- Descendentes: son aquellos que realizan el proceso a partir del símbolo inicial e intentan llegar a la cadena de entrada (lo que se ha visto en clase)
- Ascendentes: realizan el proceso a la inversa. Parten de la cadena de entrada y haciendo transformaciones a la inversa (sustituyendo la parte derecha de una regla por la parte izquierda), intentan llegar al símbolo inicial. Estas transformaciones a la inversa se llaman reducciones.
Selección de reglas
- Backtracking (No determinista): se elige una regla, y si no se llega a la cadena final, se retrocede a un punto en el que se hubiera podido seguir otra regla.
- Predictivo (determinista): cuando se presenta la situación de tener que elegirr entre varias reglas candidatas, se asegura de coger la adecuada. Nunca retrocede.
Clasificación de parsers predictivos. LL y LR
A un parser que realiza el reconocimiento de manera descendente, se le denomina LL. Los LL también se carazterizan porque realizan siempre la sustitución del símbolo más a la izquierda de la cadena primero. Si además de ser descendente, es predictivo, se le denomina parser LL(k), donde k es el número máximo de tokens que puede mirar de la entrada. Así, serán parsers LL(k):
- LL(1): aquellos que miran como máximo un token de entrada
- LL(2): aquellos que miran como máximo dos token de entrada
- …
Se denomina LR a un parser que realiza el reconocimiento de manera ascendente realizando siempre la sustitución del símbolo más a la derecha (el último). Si además de ascendente, es predictivo, se le denomina parser LR(K), donde k es el número máximo de tokens que puede mirar de la entrada. Ejemplos de parsers LR(k) serían:
- Los parsers LR(1), es decir, aquellos que miran como máximo, un token de la entrada.
- Los parsers LR(2), es decir, aquellos que miran como máximo, dos token de la entrada.
- …
Clasificación de las gramáticas
- Las gramáticas reciben el nombre directamente del parser con el que pueden ser tratadas, es decir, el nombre de la gramática indica con qué parser se puede o no implementar.
- LL(1): gramática que puede ser reconocida por un parser LL(1). Es decir, puede ser reconocida de manera predictiva (sin backtracking) sin que en ninguna situación vaya a ser necesario mirar más de un token para saber qué regla elegir
- LR(1): gramática que puede ser reconocida con un parser LR(1). Es decir, de manera predictiva y en dirección ascendente sin que nunca vaya a ser necesario mirar más de un token
- Toda gramática LL(n) también es LL(n+1), pero se usa como nombre de la misma el del parser que mire menos tokens hacia delante.
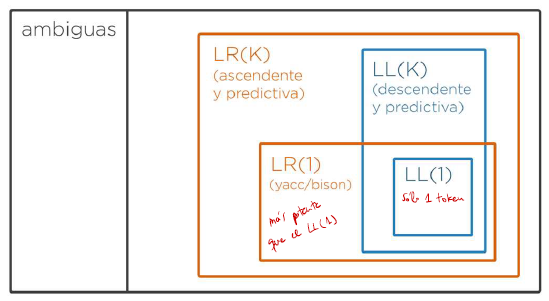
- LL(k): reconocida con un parser LL(k) de manera predictiva sin backtracking y en dirección descendente
- LR(k): reconocida con un parser LR(k) de manera predictiva y en dirección ascendente
Implementación de un parser recursivo descendente
Antes de empezar la implementación, se necesita la siguiente infraestructura que es común a cualquier parser independientemente de la gramática a implementar.
public class RecursiveParser {
private Lexicon lex;
public RecursiveParser(Lexicon lexico) throws ParseException {
lex = lexico;
advance();
}
// ------------------------------------------------------------------------
// ------ Miembros auxiliares para todo parser recursivo descendente
private Token token;
private void advance() {
token = lex.nextToken();
}
private void error() throws ParseException {
throw new ParseException("Error sintáctico en " + token.getLine() + ":"
+ token.getCharPositionInLine() + ". Lexema = " + token.getText());
}
void match(int tokenType) throws ParseException {
if (token.getType() == tokenType)
advance();
else
error();
}
// # ------------------------------------------------------------------------
// # Aquí comienza el Analizador Sintáctico
// #
public void start() throws ParseException {
...
}
}La infraestructura consiste en:
- Un método advance que lea el siguiente token.
- Un método error donde se centraliza el procesamiento de los errores sintácticos.
- Un método match que compruebe si el token actual es el indicado en el parámetro. Si es así, pasa al siguiente token. En caso contrario, notifica de que la entrada no es válida.
Debajo de estos métodos, empezarían ya los métodos propios de la gramática
Implementación de una regla
La técnica recursiva descendente se basa en implementar un método por cada regla de la gramática, siendo el consecuente de la misma el que indique su implementación.
Por ejemplo, supóngase la siguiente gramática:
start ⟶ IDENT a NUM
a ⟶ NUM IDENT
Con la anterior gramática, sería válida una entrada como:
hola 24 mundo 48
Lo primero que hay que hacer es especificar e implementar el léxico necesario para dicha gramática:
lexer grammar Lexicon;
NUM : [0-9]+;
IDENT : [a-zA-Z][a-zA-Z0-9_]*;
WS : [ \t\r\n]+ -> skip;Ahora ya se podría hacer la implementación de la gramática:
public class RecursiveParser {
...
// start ⟶ IDENT a NUM
public void start() throws ParseException {
match(Lexicon.IDENT);
a();
match(Lexicon.NUM);
match(Lexicon.EOF);
}
// a ⟶ NUM IDENT
public void a() throws ParseException {
match(Lexicon.NUM);
match(Lexicon.IDENT);
}
}A destacar:
- Dado que hay dos reglas en la gramática, hay dos métodos en la clase RecursiveParser con el mismo nombre.
- La implementación de un método consiste en implementar cada uno de los símbolos del consecuente de la regla en el mismo orden.
- Si el símbolo es un terminal, hay que invocar al método match con dicho token. Es decir, hay que comprobar que es el token actual de la entrada y pasar al siguiente.
- Si el símbolo es un no-terminal, hay que invocar al método que implementa la regla de dicho no-terminal. Es decir, simplemente hay que poner el símbolo seguido de paréntesis.
- En la implementación de la regla del símbolo inicial (
start()), hay que hacer un últimomatch(Lexicon.EOF)para comprobar que, al acabar el análisis, no haya más tokens a la entrada (lo cual indicaría que hay una entrada inválida, ya que se debería haber acabado la entrada).
Reglas con antecedente común
Supóngase la siguiente gramática:
start ⟶ IDENT a
a ⟶ NUM b IDENT
| IDENT b IDENT
b ⟶ IDENT
A la hora de implementarla, habría que crear un método por cada regla con el nombre del antecedente de la misma. Sin embargo, en la gramática anterior se tiene dos reglas con el mismo antecedente (a).
En este caso, el mismo método implementará ambas reglas añadiendo código que decida por cual de ellas ir en función de los símbolos directores de cada una. Los símbolos directores de una regla (definido de manera muy informal, ya que no se dispone del tiempo para definirlos formalmente), son los tokens que, de estar a la entrada, indicarían que dicha regla es la que hay que seleccionar para realizar la siguiente transformación (por la que hay que ir para encontrar el camino).
En las dos reglas anteriores, los símbolos directores de cada una serían:
- En
a ⟶ NUM b IDENT, serían {NUM}. - En
a ⟶ IDENT b IDENT, serían {IDENT}
Por tanto, la implementación final sería:
public class RecursiveParser {
...
// start ⟶ IDENT a
public void start() throws ParseException {
match(Lexicon.IDENT);
a();
match(Lexicon.EOF);
}
public void a() throws ParseException {
if (token.getType() == Lexicon.NUM) {
// a ⟶ NUM b IDENT
match(Lexicon.NUM);
b();
match(Lexicon.IDENT);
} else if (token.getType() == Lexicon.IDENT) {
// a ⟶ IDENT b IDENT
match(Lexicon.IDENT);
b();
match(Lexicon.IDENT);
} else // No olvidar esta rama
error();
}
// b ⟶ IDENT
public void b() throws ParseException {
match(Lexicon.IDENT);
}
}El cálculo de los símbolos directores en este caso ha sido trivial, ya que las reglas eran muy sencillas. Sin embargo, en general, es necesario seguir un procedimiento que las calcule (a mano o con herramienta) ya que, a poco que la gramática se complique con derivaciones a vacío, no serán tan evidentes de ver a ojo.
Implementación con ANTLR. Características de ANTLR
- Admite reglas tanto en EBNF como BNF
- Genera un parser utilizando básicamente la técnica recursiva descendente. Es decir:
- Es descendente
- Es predictivo (no hace backtracking)
- Cada regla se implementa como un método. La implementación de ese método se corresponde con los símbolos de su consecuente.

Preguntas de examen
- ANTLR es una herramienta ascendente o descendente? descendente
- Una gramática L(1) puede usar recursividad iszuierda? no
- Si una gramática no pasa únicamente el algoritmo L(1), ¿es ambigua? no
Creación de gramáticas. Construcciones básicas
-
Secuencia. Una secuencia no es más que una sucesión de símbolos que indica el orden en el que deben aparecer. Es la construcción más básica y los demás son casos particulares de este.
escritura ⟶ `print` expr `;` -
Lista. Se utiliza cuando se quiere indicar que una cadena puede aparecer en la entrada varias veces seguidas. En BNF esto se expresa con recursividad.
programa ⟶ instruccion
| programa instruccion
- Composición. Se usa cuando hay unos elementos atómicos o finales y otros mayores que se crean a partir de estos (similar al patrón de diseño Composite). El caso más habitual son las expresiones.
expr ⟶ NUM // Elemento atómico
| IDENT // Elemento atómico
| expr '*' expr // Elemento compuesto
| expr '+' expr // Elemento compuesto
Nota: para ver un ejemplo, ver el ejercicio 12 en Sintáctico
Tipos de listas
- Por un lado, pueden clasificarse en función de que requieran al menos un elemento (1+) o bien que no lo requieran (0+)
- Por otro lado, las listas pueden ser sin separadores(ss) o con separadores(cs). Un separador es aquella cadena (normalmente sólo un token) que se deba intercalar entre los elementos de la lista. Un ejemplo de separador es la coma entre los argumentos de una función.
f(x, y, z)
Nótese que si hay un sólo elemento no tiene que haber separador; si hay n elementos, deberá haber n-1 separadores.
Combinando estos parámetros, se obtienen cuatro tipos de listas, donde e es el elemento que se quiere repetir y s representa al separador.
| Tipo de Lista | Cadenas que genera |
|---|---|
| 1+ss | e ee eee eeee … |
| 0+ss | ε e ee eee eeee … |
| 1+cs | e ese esese … |
| 0+cs | ε e ese esese … |
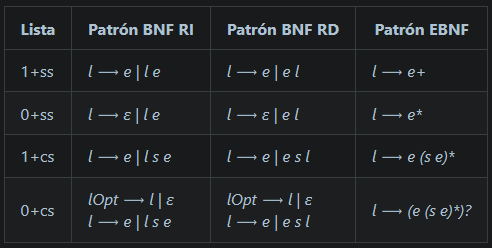
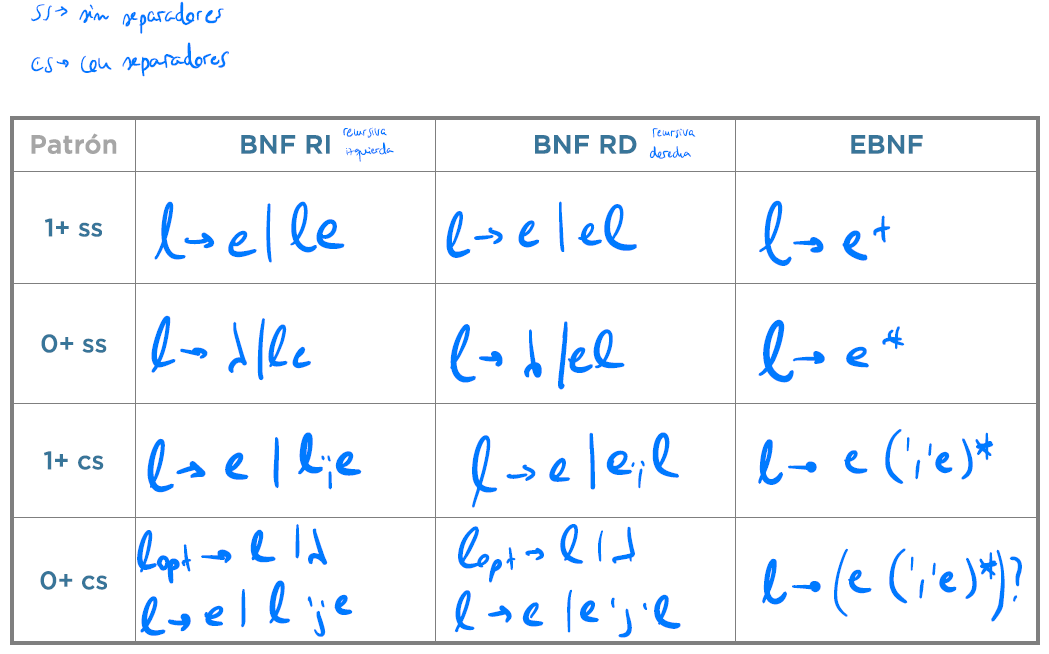
Patrones
Tabla original de Holub con una columna EBNF, donde se muestran los patrones para obtener las reglas que generen los cuatro tipos de listas anteriores:

Carácterísticas que impiden a una gramática ser LL(1)
- Que haya símbolos directores comunes
- Que tenga recursividad a izquierda
- Que sea ambigua
Símbolos directores comunes
- Son aquellos tokens de una regla que, a la hora de tener que elegir entre varias reglas, si aparecen a la entrada indican que hay que seleccionar dicha regla. Son el primer token que aparece en alguna de las cadenas: Por ejemplo:
a ⟶ IDENT IDENT
| b NUM
b ⟶ X | Y
Los símbolos directores de las dos reglas de a son:
- SD(IDENT IDENT) es sólo el token IDENT.
- SD(b NUM) son los tokens { X, Y }. Es decir, las dos cadenas que se pueden generar a partir de la cadena ‘b NUM’ son ‘X NUM’ e ‘Y NUM’. De estas cadenas, se coge el primer token de cada una.
Estos son los símbolos que vimos en la Implementación de una regla, que hay que utilizar en los if para saber por qué regla ir.
En el ejemplo anterior, la implementación de las reglas del antecedente a, usando los símbolos directores de cada regla, sería:
void a() {
if (getToken() == Lexicon.IDENT) {
match(Lexicon.IDENT);
match(Lexicon.IDENT);
} else if (getToken() == Lexicon.X || getToken() == Lexicon.Y) {
b();
match(Lexicon.NUM);
} else
error();
}Colisión de símbolos directores
A la hora de elegir entre varias reglas con el mismo antecedente, no debería haber ningún token que estuviera entre los símbolos directores de más de una de ellas. Si esto ocurriera, al aparecer dicho token en la entrada, no se sabría cual de las reglas aplicar.
Ejemplo 1
Por ejemplo, supóngase la siguiente gramática.
a ⟶ IDENT IDENT
| b NUM
b ⟶ IDENT
La implementación recursiva descendente seria:
void a() {
if (getToken() == Lexicon.IDENT) {
match(Lexicon.IDENT);
match(Lexicon.IDENT);
} else if (getToken() == Lexicon.IDENT) {
g();
match(Lexicon.NUM);
} else
error();
}Aquí se ve el problema de que un token esté entre los símbolos directores de más de una regla (con mismo antecedente). En este caso, puede verse que el token IDENT está entre los símbolos directores tanto de ‘a ⟶ IDENT IDENT’ como de ‘a ⟶ b NUM’. Por tanto, en la implementación anterior nunca se metería por la segunda rama del if.
Esto haría que una entrada válida tal como ‘a 24’ fuera erróneamente clasificada como inválida.
Ejemplo 2
En el ejemplo anterior el calcular los símbolos directores era trivial. Sin embargo, no es una tarea que se deba hacer a ojo, ya que enseguida puede complicarse la tarea, por ejemplo, en cuanto aparezcan producciones a vacío (ε). En la siguiente gramática, aunque a simple vista no se vea, hay dos reglas con el mismo antecedente que comparten símbolos directores:
s ⟶ c d g
c ⟶ NUM | IDENT
d ⟶ NUM | f g
f ⟶ PRINT NUM | ε
g ⟶ IDENT | NUM
El problema está en las dos reglas que tienen a d como antecedente.
-
En la primera regla ‘d ⟶ NUM’ es fácil ver que su único símbolo director es el token NUM.
-
En la regla ‘d ⟶ f g’, sus símbolos directores son los tokens { PRINT, IDENT y NUM }.
El primer token se obtiene si f se sustituye aplicando la primera de sus reglas. Pero f también puede sustituirse por su segunda regla y anularse. En este caso, serían los símbolos directores de g (IDENT y NUM) los que formarían parte de los símbolos directores de d.
Por tanto, el token NUM forma parte de los símbolos directores de ambas reglas de d.
Este ejemplo pretende mostrar que no es conveniente calcular los símbolos directores a ojo, ya que a veces se pueden pasar por alto ciertas situaciones, y por ello que se debe comprobar la gramática antes de implementarla usando una herramienta.
Posibles soluciones
Las opciones más comunes a la hora de implementar una gramática que no sea LL(1) son:
- Leer más tokens de la entrada.
- Cambiar de dirección de reconocimiento del parser.
- Buscar una gramática equivalente.
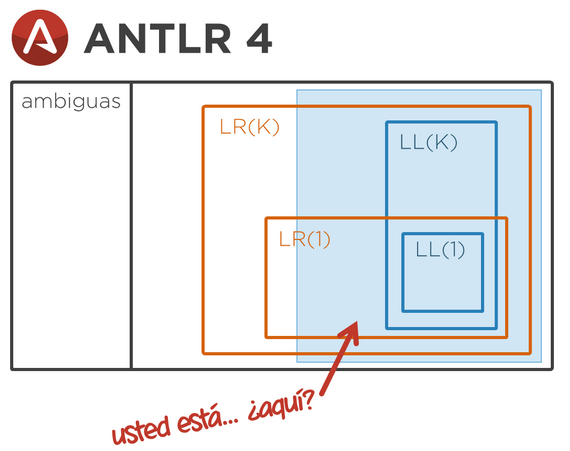
¿Qué hace ANTLR?
- Ante una gramática que presente reglas con el mismo antecedente y símbolos directores comunes, opta por leer más tokens de entrada. En vez de quedarse en k=1, sigue mirando tantos tokens como sea necesario.
Recursividad a la izquierda
- Se dice que una regla es recursiva cuando el antecedente aparece en el consecuente de la regla:
a ⟶ ... a ...Se dice que una regla es recursiva a izquierda (RI) cuando el antecedente aparece como primer símbolo del consecuente.
a ⟶ a ...Problema de la recursividad a la izquierda
- Los bucles infinitos:
a ⟶ a ...
void a() {
a();
...
}Posibles soluciones
A diferencia del capítulo anterior, aquí no es solución mirar más tokens hacia adelante. Las alternativas que sí permanecen son las otras dos:
- Cambiar de dirección de reconocimiento del parser.
- Buscar una gramática equivalente sin RI. Regla para eliminar la recursividad a la izquierda
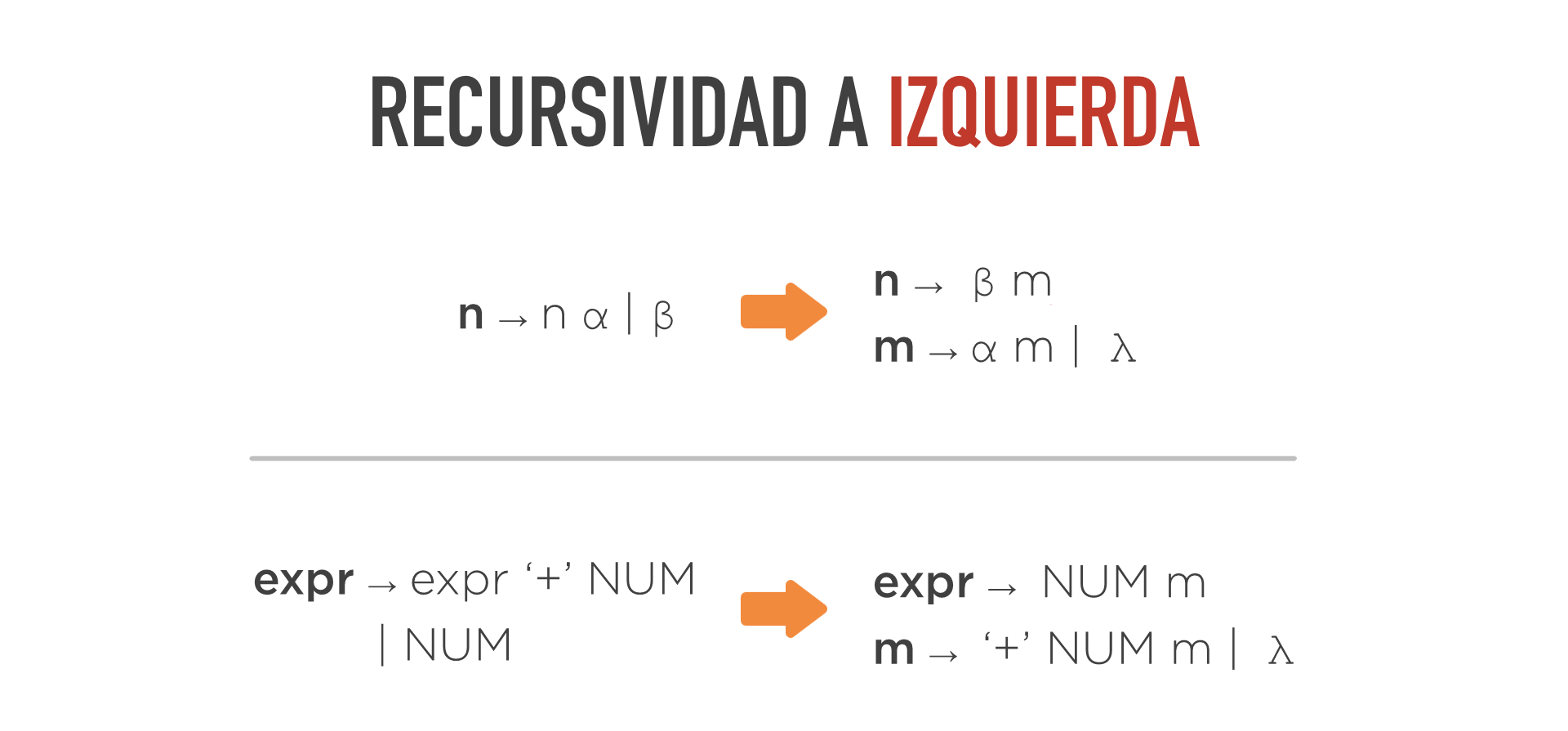
¿Qué hace ANTLR?
ANTLR es un parser recursivo descendente. Por tanto, no puede implementar una gramática con recursividad a izquierda. Pero lo que sí hace, de manera automática, es transformar la gramática tal y como se acaba de ver en el apartado anterior. Y es esta otra nueva gramática (que no tiene RI) la que realmente implementa.
Pero ANTLR no puede tratar todo tipo de recursividad a izquierda. Sólo puede tratar la recursividad a izquierda directa, es decir, cuando la recursividad se halla en la propia regla (que son los ejemplos vistos anteriormente). Sin embargo, si la gramática tiene recursividad a izquierda indirecta, no puede transformarla y la gramática es rechazada.
Un ejemplo de recursividad a izquierda indirecta seria el siguiente, en el cual ANTLR produciría un error.
a ⟶ b ...
b ⟶ a ...
Ambigüedad
En el tema anterior se vio cómo se registraba en un árbol concreto (o de análisis sintáctico) Árbol Concreto (o de Análisis Gramatical) el camino encontrado para llegar desde el símbolo inicial hasta la cadena de entrada (lo cual prueba que es una entrada válida)
Concretamente, se vio esta gramática y un árbol para la entrada que la sigue.
s ⟶ e
e ⟶ e + e
e ⟶ e * e
e ⟶ LITENT
3 + 4 * 5
Sin embargo, existe otra forma de llegar a dicha entrada partiendo de s (y, por tanto, existe otro árbol concreto distinto). Estos son los dos árboles que se pueden obtener para la entrada:
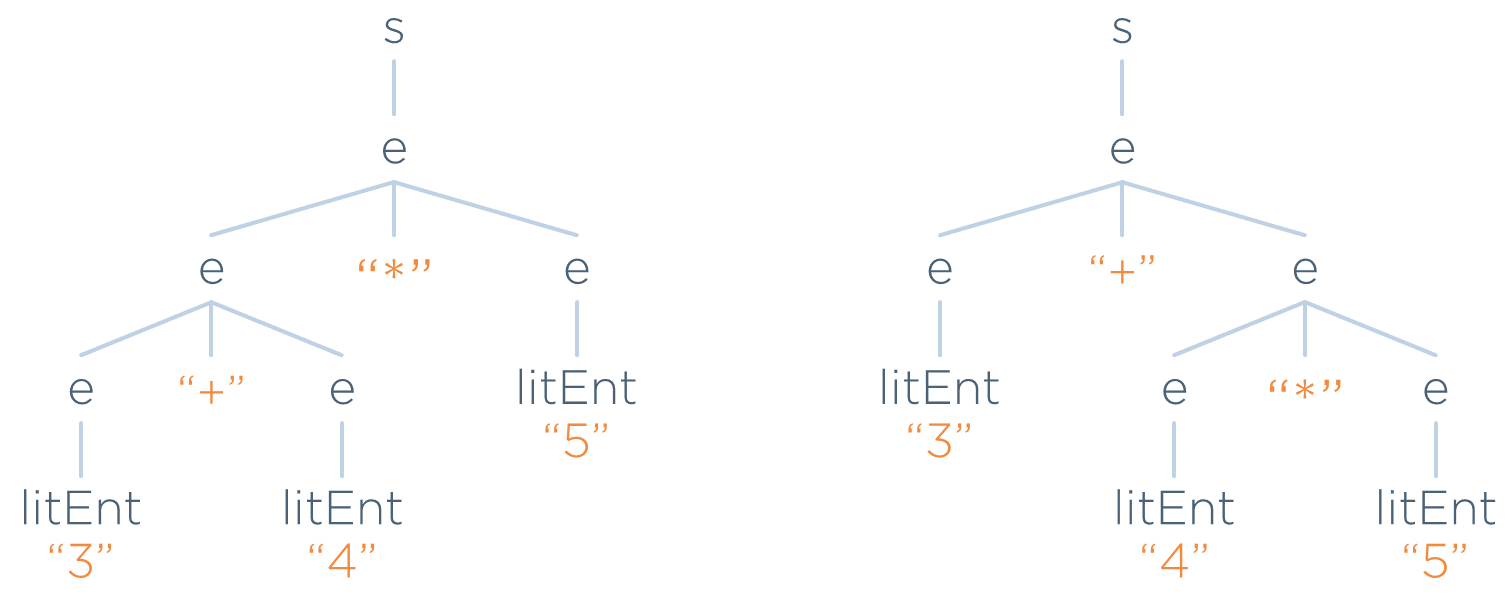
Esto ocurre por que la gramática anterior es ambigua.
Posibles soluciones
Las soluciones más comunes ante una gramática ambigua son:
- Como en las situaciones anteriores, siempre hay la opción de hallar una gramática equivalente.
- Cambiar el lenguaje.
- Usar reglas de selección.
¿Qué hace ANTLR?
ANTLR acepta gramáticas ambiguas con reglas de selección para indicar qué interpretación se debe hacer de las entradas con más de una interpretación.
Ejemplo
Supóngase la siguiente especificación de ANTLR.
start : 'print' expr ';';
expr : NUM
| IDENT
| expr '+' expr
| expr '*' expr;Supóngase la entrada:
print 1 + 2 * 3;
Dado que la gramática anterior es ambigua, la entrada podría reconocerse de dos formas: una en que se realiza primero la suma y otra en la que se hace primero la multiplicación.
Sin embargo, ANTLR usar el orden de las reglas para extraer la regla de selección por la cual se quiere elegir el árbol en el que el ’+’ tiene mayor prioridad. Por tanto, tomaría la interpretación de la izquierda (realiza antes la suma).
Esta, obviamente, no es la que se corresponde con la precedencia real de los operadores aritméticos. La forma de indicarle que se quiere el otro árbol es cambiando el orden de las dos reglas de los operadores ’*’ y ’+‘.
start : 'print' expr ';';
expr : NUM
| IDENT
| expr '*' expr;
| expr '+' expr
Ahora, sí que ANTLR interpretaría la entrada de la forma correcta dando más prioridad al ’*’ y se formaría el árbol de la derecha.
Problemas del árbol concreto
- Es redundante
- Está acoplado a la gramática
Ejemplo de redundancia
Supóngase la siguiente gramática.
programa ⟶ sentencia | sentencia programa (1+ss)
sentencia ⟶ escritura
| while
escritura ⟶ PRINT ID ‘;’
while ⟶ WHILE ID ‘{‘ programa ‘}’
Lo siguiente sería una entrada válida.
print a;
while a {
print b;
}Y el árbol concreto de la misma sería el siguiente.
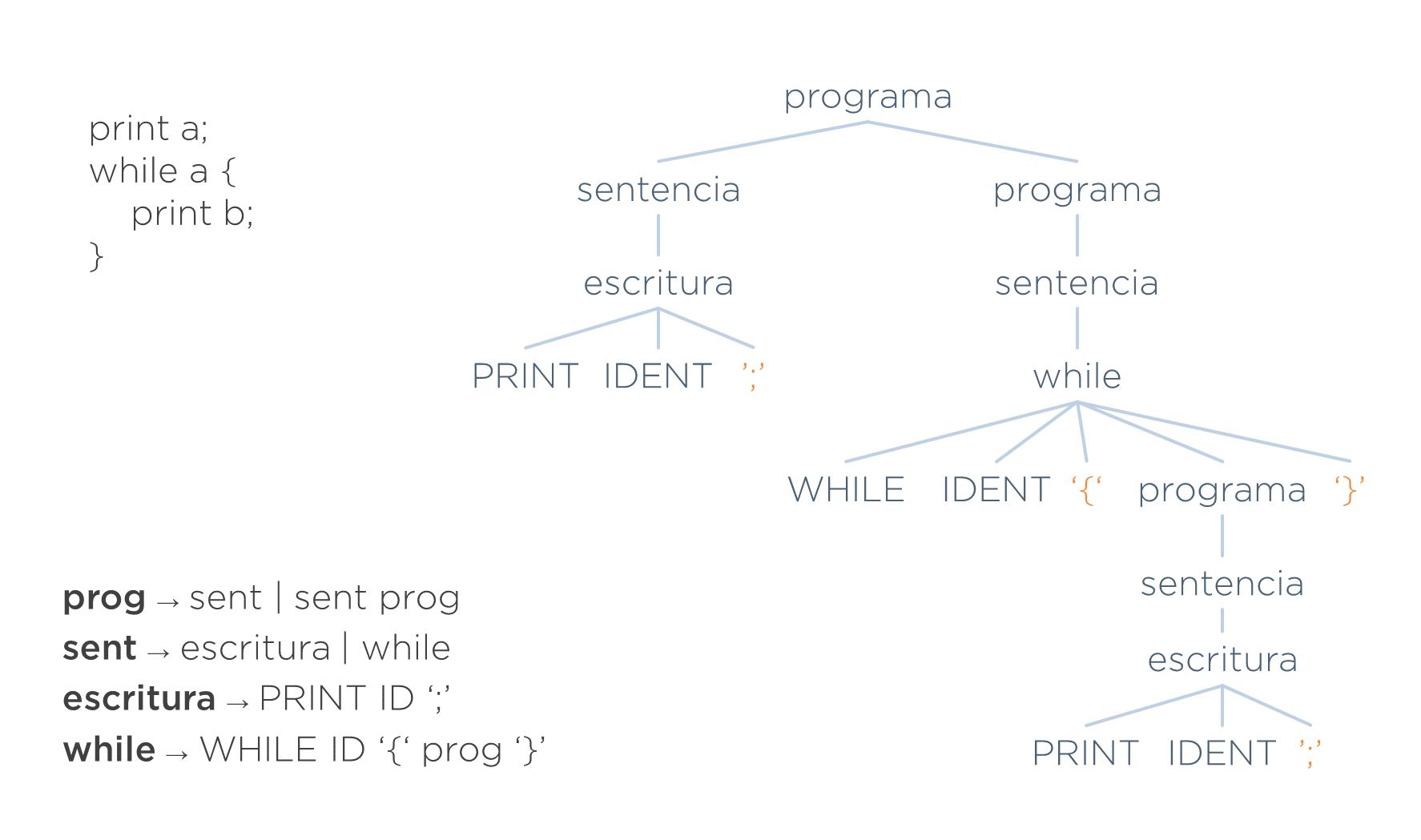
En este árbol hay tres grupos de símbolos redundantes. En la imagen posterior se identifican dichos símbolos:
- Sobran los tokens que ayudaron a identificar una estructura (tokens PRINT y WHILE — tachados en rojo). Ya no son necesarios ya que su nodo padre ya indican qué estructuras son (escritura y while respectivamente).
- Sobran los tokens que ayudan a delimitar las estructuras (las llaves y los punto y coma — tachados en azul). Las llaves, por ejemplo, se utilizaban para indicar qué va dentro del while y qué va fuera. Ahora ya no son necesarias, ya que la propia estructura del árbol deja claro qué sentencias están dentro del mismo.
- Sobran los no-terminales necesarios para definir las producciones de la gramática pero que son redundantes en el árbol (sentencia y algunos programa — tachados en amarillo). Por ejemplo, no aporta nada que encima de un nodo escritura haya otro nodo indicando que es una sentencia.
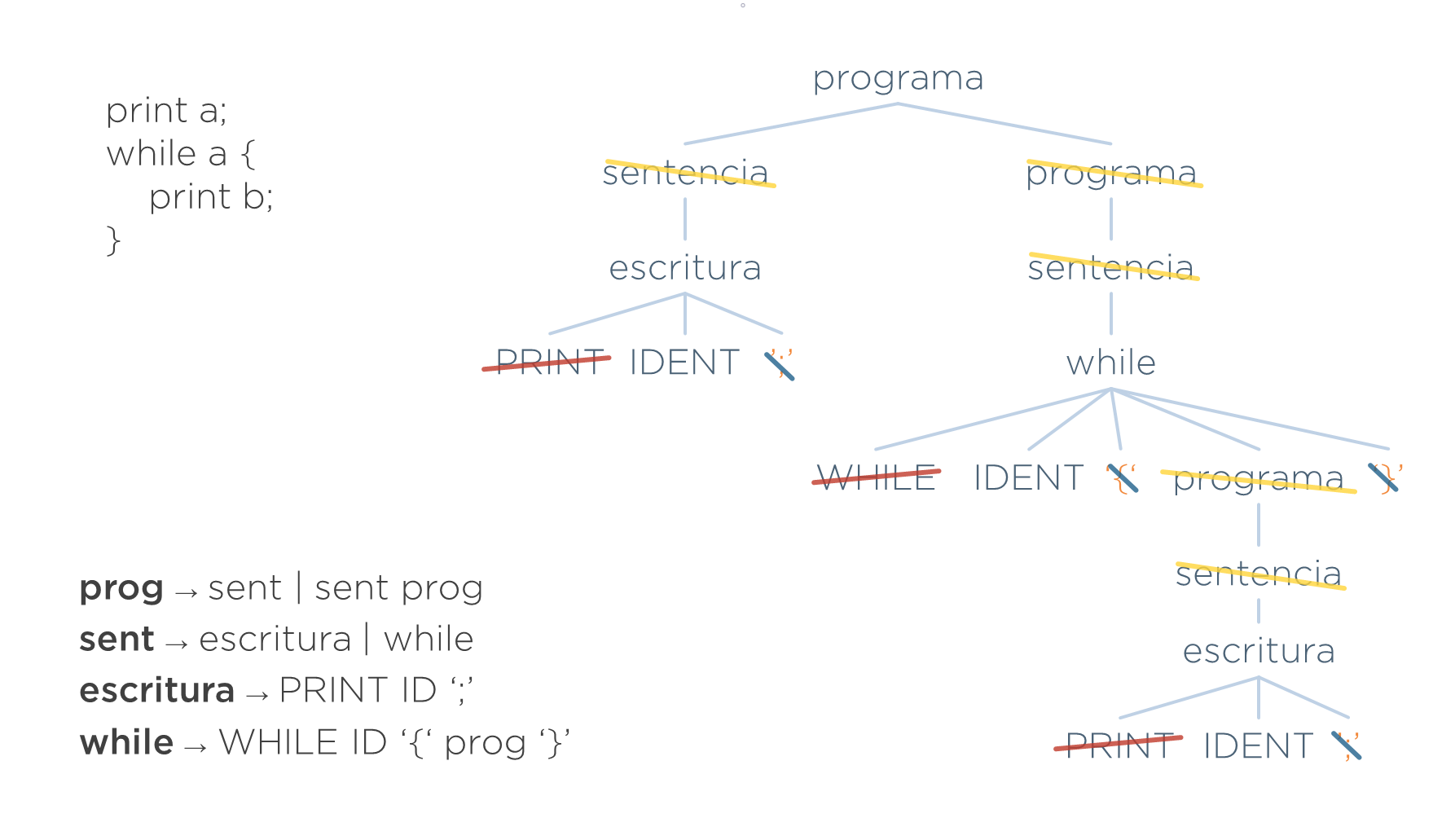
Este es el primer problema de utilizar un árbol concreto. Hay mucho nodo innecesario que:
- Si se elimina, no va a suponer una pérdida de información para las fases posteriores del traductor.
- Pero si se deja supone:
- Un gasto de memoria.
- Y, lo que es más importante, complicaría la implementación de las siguientes fases, ya que tienen que implementar recorridos de más nodos de los necesarios.
Ejemplo de acoplamiento
En la siguiente imagen se puede ver una gramática, una entrada válida y el árbol concreto que se crearía para ella.
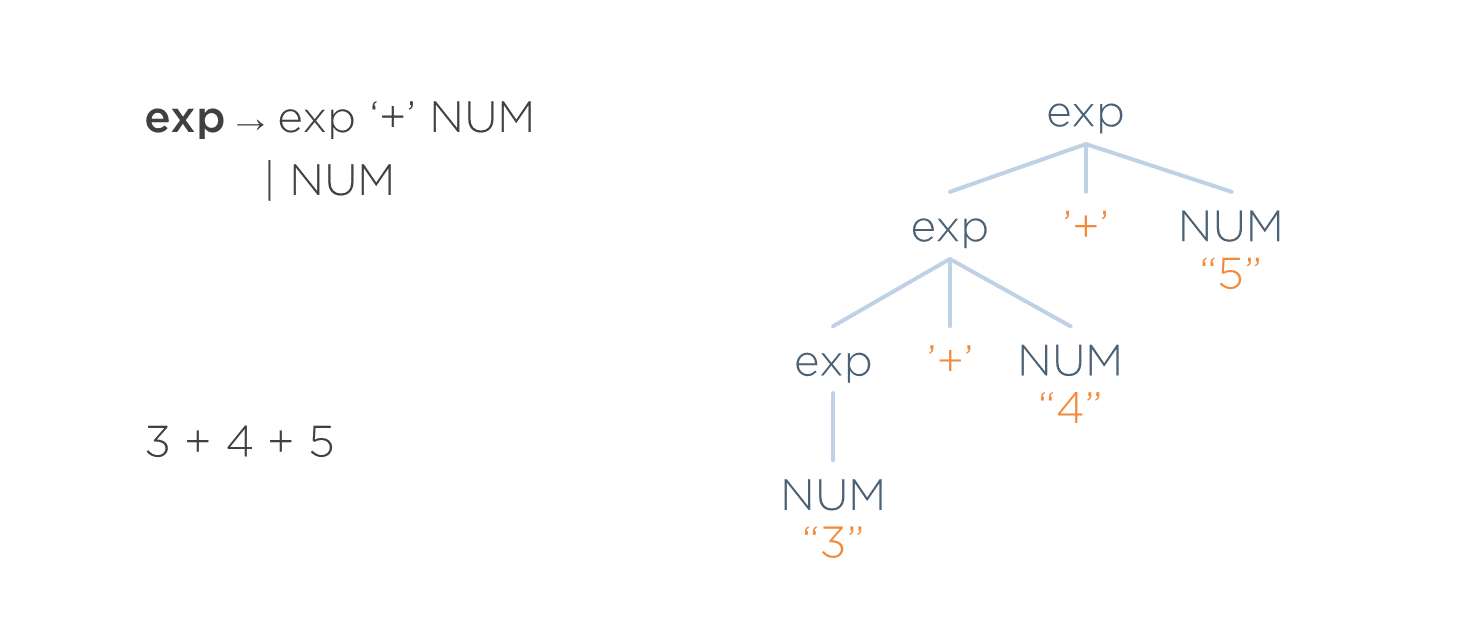
Supóngase que el sintáctico, en vez de pasar un AST, les pasara el árbol concreto a las fases posteriores. Por tanto, todas las fases posteriores del traductor se implementarían en función de dicha estructura de árbol.
Supóngase que, una vez implementadas las demás fases, se decide refactorizar la gramática (recuérdese que de un mismo lenguaje existen infinitas gramáticas equivalentes). Por tanto, sin cambiar el lenguaje a reconocer, se opta por reconocerlo con una nueva gramática. En la siguiente imagen se ve a la izquierda la gramática antigua con el árbol concreto que generaba y a la derecha la nueva gramática con el árbol concreto que genera para la misma entrada.
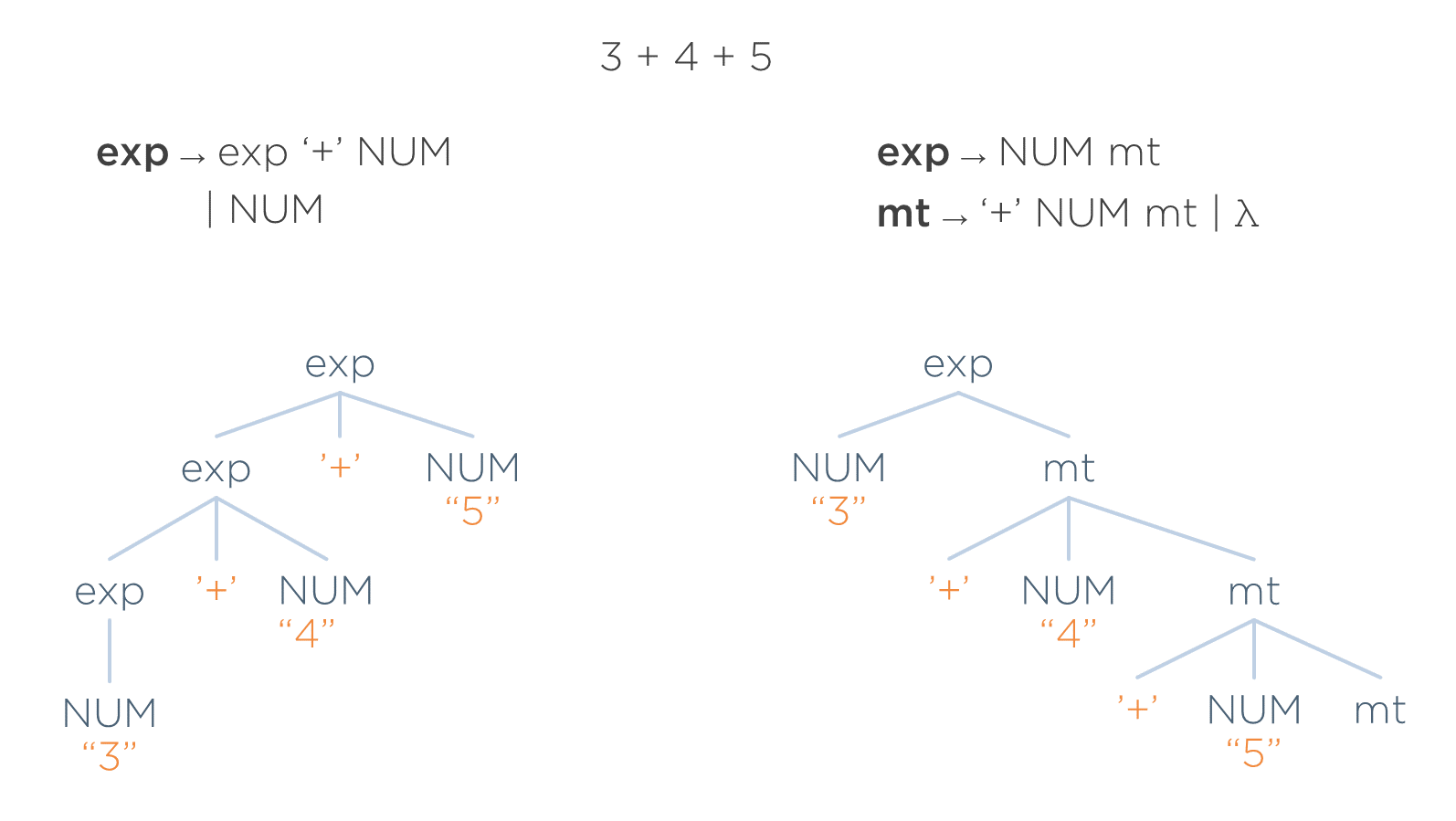
El lenguaje no se ha cambiado. Y se debería esperar que las consecuencias del cambio sean nulas para las siguientes fases. Sin embargo, dado el acoplamiento que tiene el árbol concreto con la gramática (ya que usa los mismos símbolos y estructura que esta), el árbol que se genera es distinto. Por ejemplo, ahora aparece un nodo mt que antes no estaba. Esto supone que habría que cambiar todas las fases posteriores del traductor ya que ha cambiado el árbol y hay que adaptarlas para que recorran los nuevos nodos (y que dejen de recorrer los que desaparezcan).
Si el lenguaje no ha cambiado, no debería cambiar tampoco la estructura del árbol — aunque se hubiera cambiado la gramática. Las reglas que utilice un sintáctico debería ser un asunto interno del mismo que no debería afectar a otras fases. No tiene sentido dividir el trabajo de un traductor en fases si luego tienen un acoplamiento tan grande con el sintáctico. Este es el principal problema de usar un árbol concreto.
Árbol de Sintaxis Abstracto (AST)
- Se crea en lugar del árbol concreto debido a los problemas que éste presenta.
- El AST es el árbol mínimo que preserva la semántica de entrada. No tiene los problemas del árbol concreto:
- No tiene nodos redundantes, pues deja en ellos la información mínima
- Aunque cambie la gramática, si el lenguaje no cambia, el AST generado para una misma entrada sigue siendo el mismo, pues no se basa en símbolos de la gramática para crear los nodos
¿Cómo se obtiene?
- El AST tiene que tener como nodos los símbolos de la gramática. Han de estar identificados y definidos y tienen que ser:
- suficientes nodos como para que se pueda representar en forma de árbol cualquier entrada válida del lenguaje
- y solamente esos nodos (que no haya nodos que se pudieran eliminar sin perder información)
- El AST no se obtiene a partir del árbol concreto. Sus nodos no tienen ninguna relación.
- Se debe diseñar el AST con el objetivo de que facilite al máximo las tareas que tengan que realizar las fases que lo van a utilizar. Por tanto, hay que determinar:
- Qué nodos/objetos se necesitan
- Con qué propiedades
- Qué relaciones hay entre los nodos (padre-hijo, composición…)
Ejemplo
Supóngase la siguiente entrada:
print a;
while a {
print b;
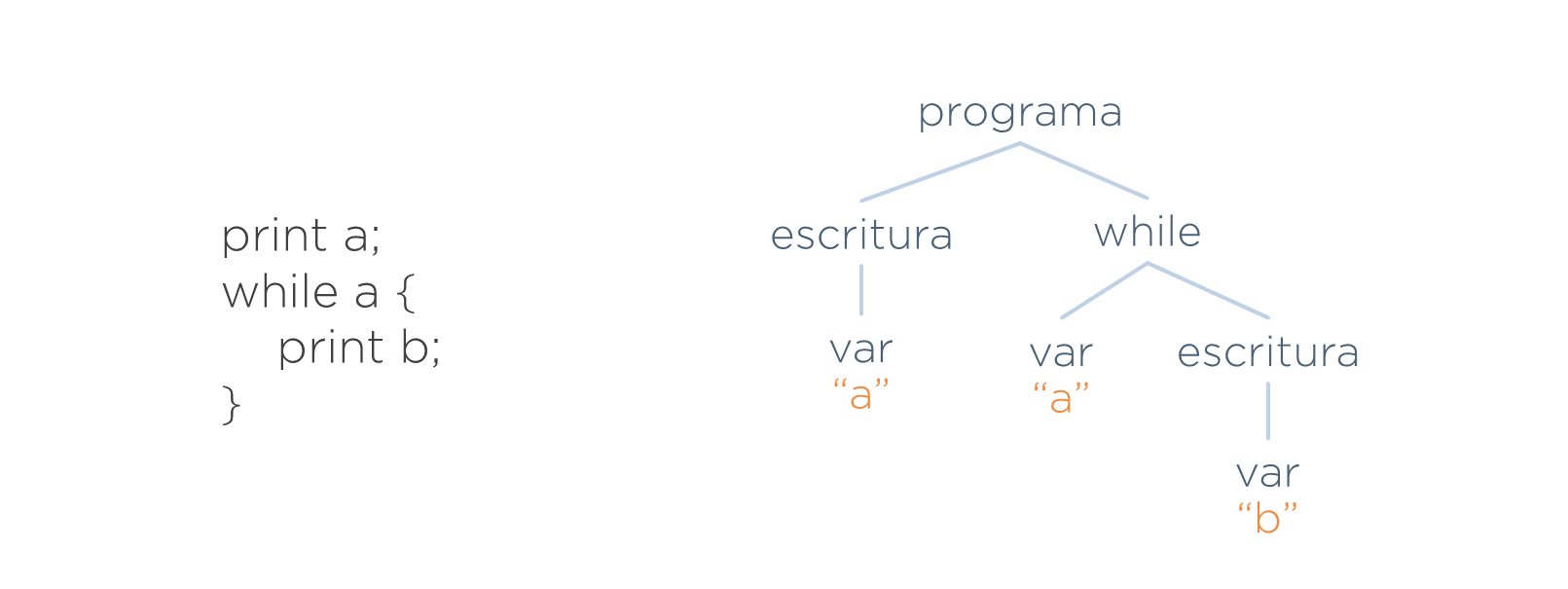
}¿Cuál es la información mínima que representa lo que hace dicho programa? Una forma de averiguarlo, por ejemplo, sería plantearse qué es lo único que necesitan saber de esa entrada las demás fases (por ejemplo, el generador de código). En el caso de la entrada anterior, la esencia de dicha entrada es:
- Que hay dos sentencias: una escritura y un bucle while.
- La escritura imprime el valor de a (no aporta nada el punto y coma para generar el código).
- La condición del while es el valor de la a y, si se cumple, imprime b.
Pues esa esencia es lo único que debe incluir el AST de dicha entrada.
Comparativa AST vs. Árbol concreto
Se pueden comparar el árbol concreto y el AST de la misma entrada.
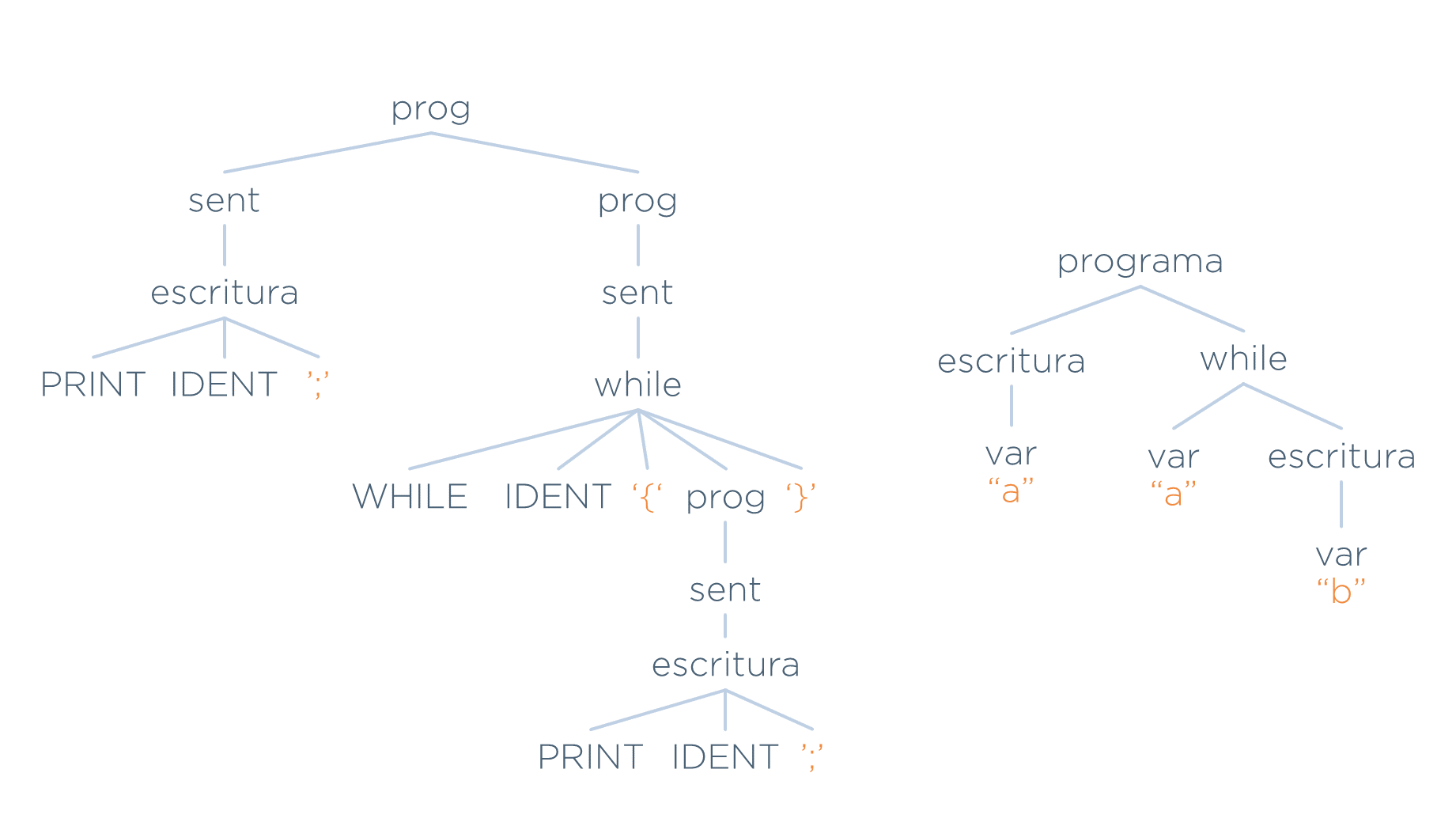
Como puede observarse:
- El AST es mucho más pequeño y fácil de entender.
- El AST no está acoplado a la gramática, ya que la estructura del árbol no se basa en la forma de las producciones de ésta.
Diseño de un AST
Supóngase que se quiere diseñar el AST para un lenguaje del cual la siguiente entrada es un ejemplo.
a = 2;
while (a < 100) {
read b;
a = a + b ;
}La especificación informal del lenguaje es:
- No tiene definición de variables.
- Sólo tienen las sentencias que se ven en el ejemplo.
- Los operadores aritméticos son los cuatro básicos (suma, resta, multiplicación y división). Los relacionales son el mayor, menor e igual.
Proceso de diseño de un AST
- Identificar los nodos necesarios del lenguaje
- Determinar los hijos de cada uno
Identificar nodos
Según el enunciado anterior, para modelar cualquier entrada serán necesarios los siguientes nodos. Con ExprBin (expresión binaria) se representarán tanto las operaciones aritméticas como las relacionales

Identificar hijos
Hay que determinar qué hijos tendrá cada nodo. Por cada hijo se crea una rama. Además, a cada rama se le asocia un tipo — el tipo que deben tener los nodos que se quieran conectar en dicha rama. Si no se le pusiera ningún tipo significaría que en dicha rama se podría poner como hijo cualquier nodo. El tipo supone, por tanto, una forma de expresar las restricciones a la hora de conectar nodos.
 A la hora de elegir un tipo para una rama habrá que elegir uno de entre los tres casos siguientes:
A la hora de elegir un tipo para una rama habrá que elegir uno de entre los tres casos siguientes:
- El tipo es otro nodo.
- El tipo es una categoría sintáctica. Cuando un nodo pueda tener como hijo a nodos de distintos tipos, en vez de indicar cada uno en la rama, se define una categoría sintáctica con todos ellos y es el nombre de ésta la que se pone como tipo de la rama (es decir, es un atajo para poner varios tipos).
- El tipo es un tipo propio del lenguaje de implementación del AST. La mayoría de las veces será el tipo string del lenguaje.
Además, si en una rama es multivaluada (puede haber varios hijos en ella) se pondrá un ’*’ en el tipo para indicarlo. Adelantándonos a la implementación, que se verá más tarde, ya se puede intuir que esta rama se implementará como una lista.
Con lo anterior, quedaría el siguiente diseño de nodos.
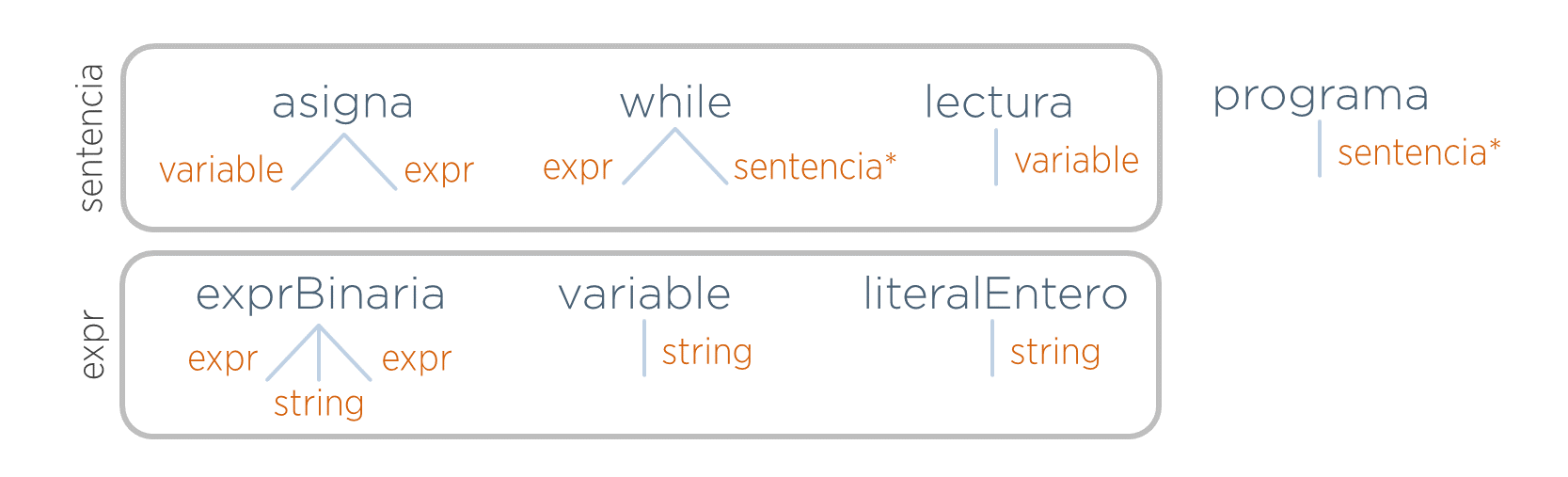
Gramáticas Abstractas
- Metalenguaje para documentar los AST.
- Se define una regla por cada nodo
- Sigue la siguiente estructura:
- Comienza por el nombre del nodo
- Si pertenece a categorías sintácticas, se ponen todas ellas detrás del nombre separadas por dos puntos
- A continuación, separados por una flecha, aparecen los tipos de los hijos del nodo
<nodo>:<categorías> -> <tipos hijos>
En el capítulo anterior se llegó al siguiente diseño de nodos expresado de forma gráfica:

Se describen ahora dichos nodos usando la notación de las gramáticas abstractas:

Nótese que lo obligatorio es poner el tipo de los hijos (no el nombre). Sin embargo, cuando varios hijos tienen el mismo tipo, puede ser de ayuda asignar nombres a los hijos para facilitar la lectura de la gramática. Para poner un nombre a un hijo basta con ponerlo delante del tipo separándolos con dos puntos. La siguiente gramática es el resultado de añadir nombres (en gris) a ciertos hijos para facilitar su comprensión.

Aclaraciones adicionales:
- No confundir el operador
'*'con el uso que se da a dicho carácter en EBNF y en las expresiones regulares. En estas últimas, dicho operador indica la repetición de cero o más elementos. Aquí simplemente significa que dicha rama, en vez de un sólo nodo, debe tener una lista de ellos. Por tanto, no hay — y no se necesita — el operador ’+‘. Una vez indicado que dicha rama es una lista, no es relevante si en esa lista habrá al menos un elemento o no. - Todo hijo es opcional. Si no se usa el
'*', se crea una referencia a un nodo en vez de una lista. Es asunto ya de la implementación que dicha referencia se use o no. Por tanto, no se necesita operador para indicar opcionalidad (’?’). - Recuérdese que, tal y como se dijo en el capítulo anterior, el tipo no es texto libre, sino que debe ser un nodo, una categoría sintáctica o un tipo propio del lenguaje de implementación
GLC vs. Gramática Abstracta
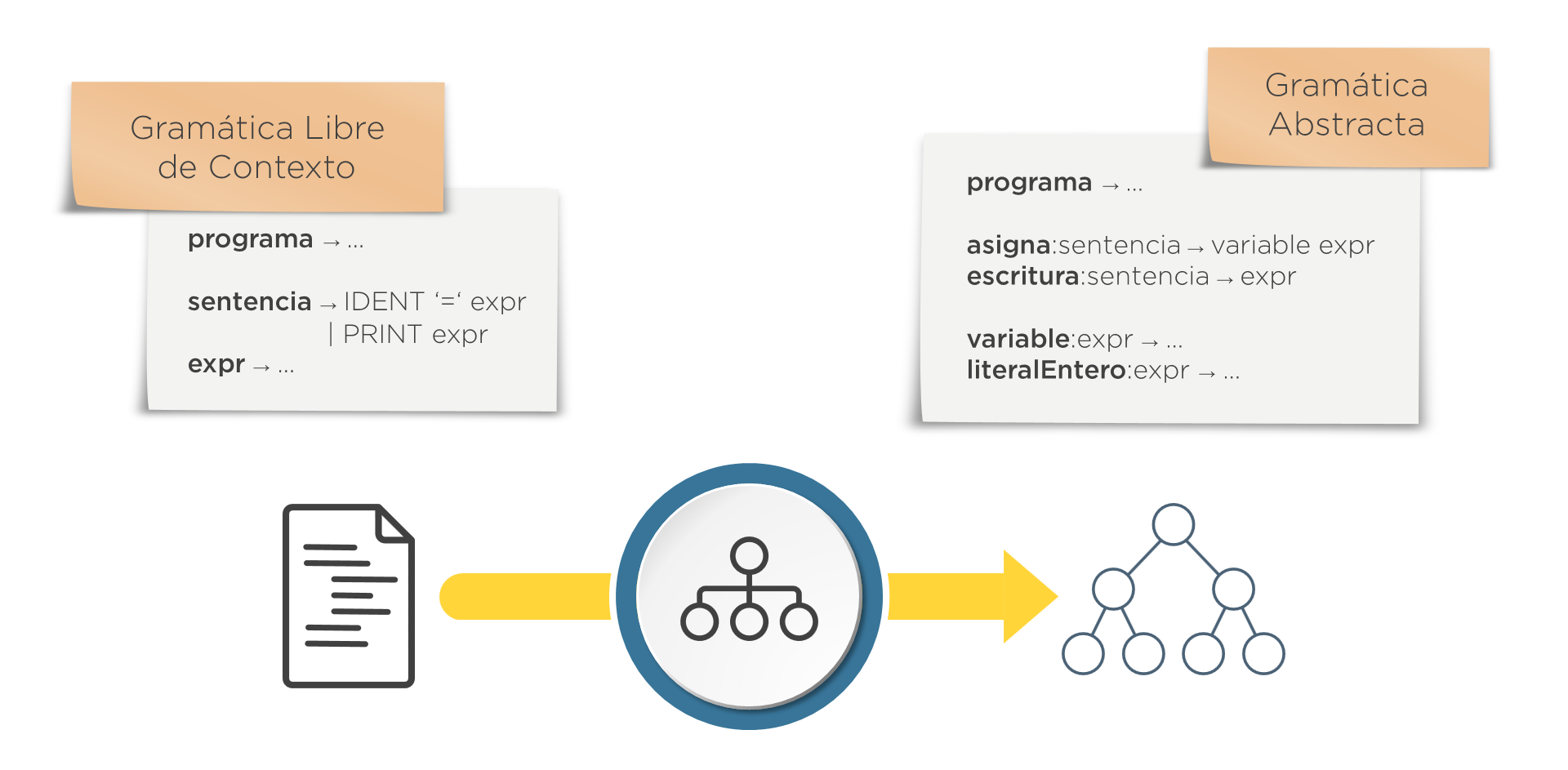
- La GLC determina cómo tiene que ser la entrada del sintáctico. Describe la estructura de textos. Es la forma de indicar al usuario del compilador cómo debe escribir una entrada válida.
- La gramática abstracta es la que determina cómo va a ser la salida del sintáctico. Describe la estructura de árboles. Es la forma de indicar a los diseñadores de las demás fases del traductor cómo van a ser los árboles que reciban.
Ver el ejercicio 15 en Sintáctico
Implementación del AST. Implementación de los Nodos
- Hay que seguir las indicaciones de la gramática abstracta
- Hay que seguir el siguiente proceso:
- Se crea un interfaz AST que será el tipo común de todos los nodos.
- Por cada categoría sintáctica se crea un interfaz con el mismo nombre. Dicho interfaz derivará del interfaz AST.
- Por cada regla (es decir, por cada nodo) se crea una clase del mismo nombre que el nodo. Dicha clase implementará los interfaces de las categorías sintácticas a las que pertenezca (o AST si no pertenece a ninguna).
- La parte derecha de cada regla indica los atributos que debe tener la clase Java creada para dicha regla.
- Por cada hijo, se crea una propiedad Java del tipo del mismo.
- Si no se indica el nombre de un hijo (ya que sólo su tipo es obligatorio), se puede poner cualquier nombre suficientemente explicativo.
- Si el hijo tiene
'*'asociado a su tipo, se crea una lista de dicho tipo. En caso contrario, se añade simplemente una referencia a un sólo objeto. Por ejemplo, supóngase la siguiente gramática abstracta.
programa ⟶ sentencias*
asigna:sentencia ⟶ variable expr
while:sentencia ⟶ expr sentencias*
lectura:sentencia ⟶ variable
exprBinaria:expr ⟶ left:expr operador:string right:expr
variable:expr ⟶ nombre:string
literalEntero:expr ⟶ valor:stringSu implementación sería:
interface AST { }
interface Sentencia extends AST { }
interface Expr extends AST { }
class Programa implements AST {
List<Sentencia> sentencias;
}
class Asigna implements Sentencia {
Variable variable;
Expr expr;
}
class While implements Sentencia {
Expr expr;
List<Sentencia> sentencias;
}
class Lectura implements Sentencia {
Variable variable;
}
class ExprBinaria implements Expr {
Expr left;
String operador;
Expr right;
}
class Variable implements Expr {
String nombre;
}
class LiteralEntero implements Expr {
String valor;
}Creación del AST
Crear el AST implica hacer los new de los distintos nodos del árbol en algún punto del analizador sintáctico. Se trata ahora de determinan dichos puntos.
El AST debe reflejar lo que se ha ido encontrando en la entrada ¿Cuándo se querrá crear, por ejemplo, un nodo que represente a una sentencia print? Pues después de haber encontrado todos los símbolos de dicha estructura en la entrada.

En ANTLR
Enlazar nodos
print: PRINT expr ';' { ... = new Print(...); } ;Devolución de valores
print returns[Print ast]
: 'print' expr ';' { $ast = new Print(...); }
;
expr returns[Expresion ast]
: ...
;Obtención de valores
print returns[Print ast]
: 'print' expr ';' { $ast = new Print($expr.ast); }
;
expr returns[Expresion ast]
: ... { $ast = ... }
;La directiva returns sirve para dos cosas:
- Para indicar el tipo de retorno que debe tener el método que ANTLR implemente a partir de dicha regla.
- Para crear una variable (en este caso ast) donde las acciones podrán dejar el valor de retorno de la función (ya que no pueden usar la sentencia return de Java). Para usar esta variable en las acciones, ANTLR exige prefijar su nombre con el carácter (por eso en la acción se asigna a $ast).
Ver el ejercicio 16 en Sintáctico
Creación de Listas
Una vez que tenemos aisladas las reglas que implementan los patrones, a la hora de crear los nodos de un AST, ¿qué acciones Java hay que añadir a dichas reglas-patrones? En la siguiente tabla se muestra qué acciones hay que añadir y dónde en función del patrón que representa la regla:
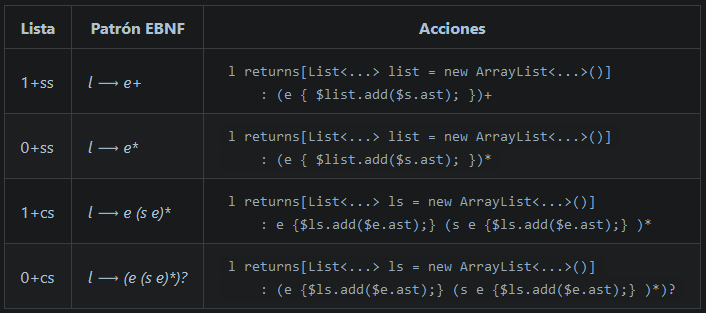
Ver el ejercicio 17 en Sintáctico
Mirar más ejercicios en Sintáctico
Análisis semántico
Supóngase la siguiente entrada:
print v[i] + 2;¿Qué cosas podrían estar mal en cuanto a las sentencias anteriores?
- Que v no esté definida
- Que i no esté definida
- Que i esté definida pero no sea de tipo entero
- Que v esté definida pero no sea un array
- Que
v[i]fuera de tipo no numérico, y no se pudiese sumar con el 2
Se subdivide en dos fases:
-
Identificación
-
Comprobación de tipos
-
Sintaxis: conjunto de reglas formales (gramática) que definen la estructura correcta de los programas de un lenguaje.
-
Semántica: conjunto de reglas formales que definen el significado de los programas sintácticamente correctos.
-
Los intérpretes tienen que conocer toda la semántica que hay.
-
El análisis semántico de un procesador de lenguaje es la fase que hace cumplir las reglas semánticas del lenguaje. Es la última oportunidad para detectar errores en el programa. Después de esta fase comienzan las fases de síntesis.
Fase de Identificación
- Comprueba que todo símbolo que se use en el programa (variables, funciones, estructuras, clases…) haya sido definido en algún lugar del programa. Si no es así no tiene sentido seguir compilando
- Si volvemos al ejemplo
print v[i] + 2;esta etapa detectaría que las variables v e i estén definidas en el programa:
Ejemplo de realización de la etapa:
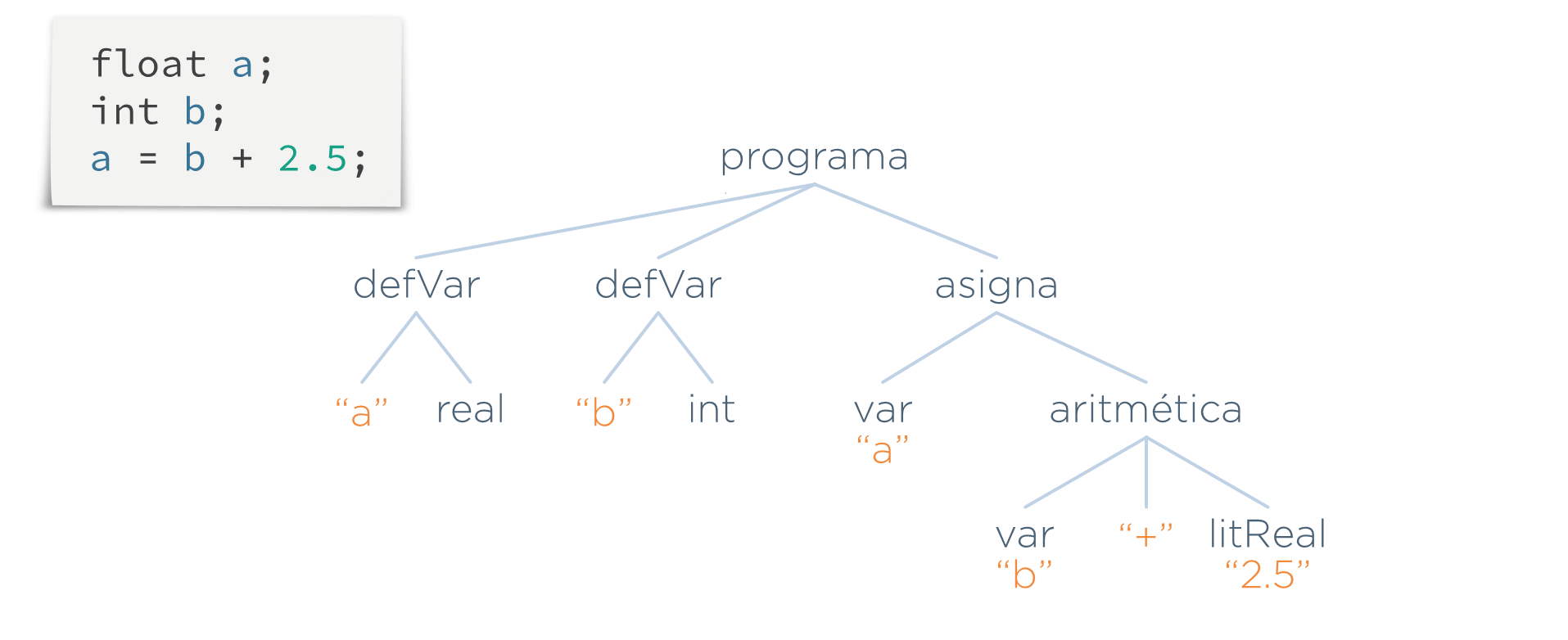
Lo que hace esta etapa es recorrer el AST, y cada vez que encuentre una referencia a una variable (un nodo var), se busca si existe una definición con el mismo nombre de la variable (un nodo defVar)
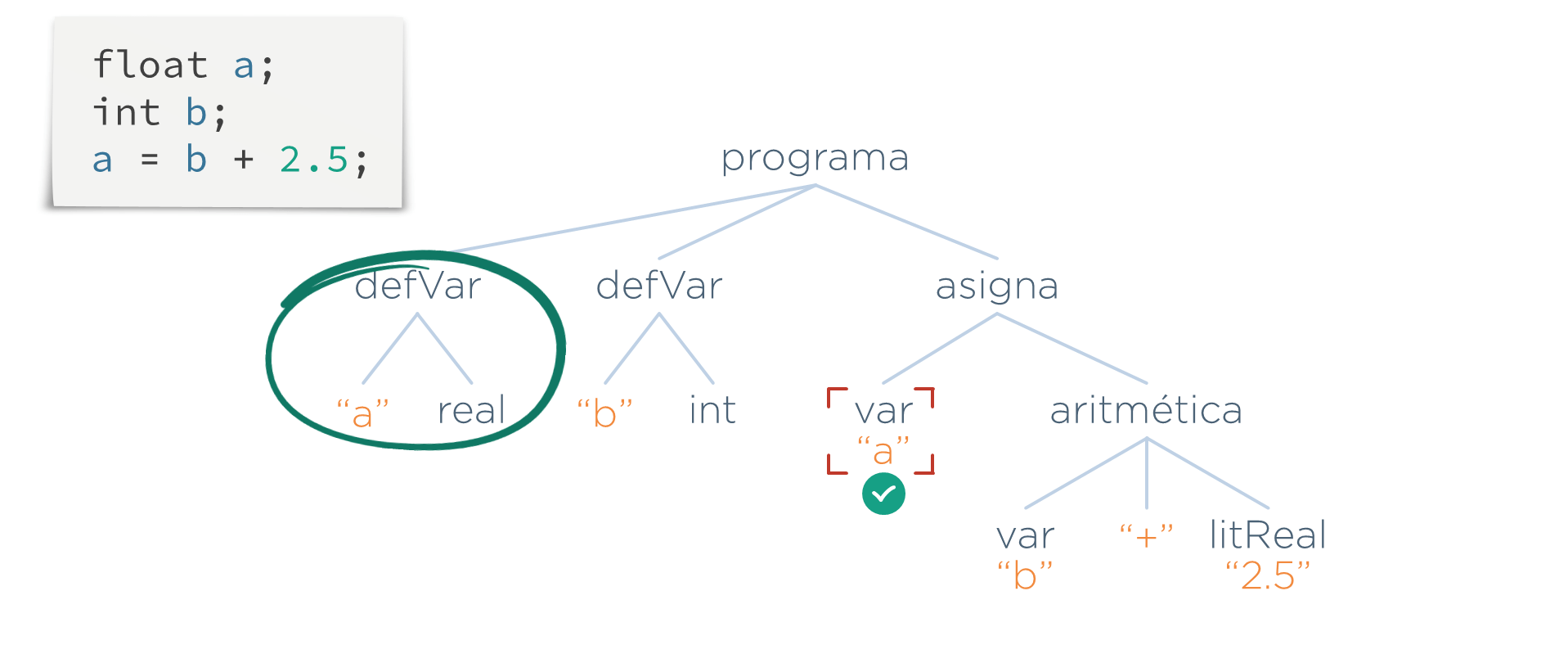
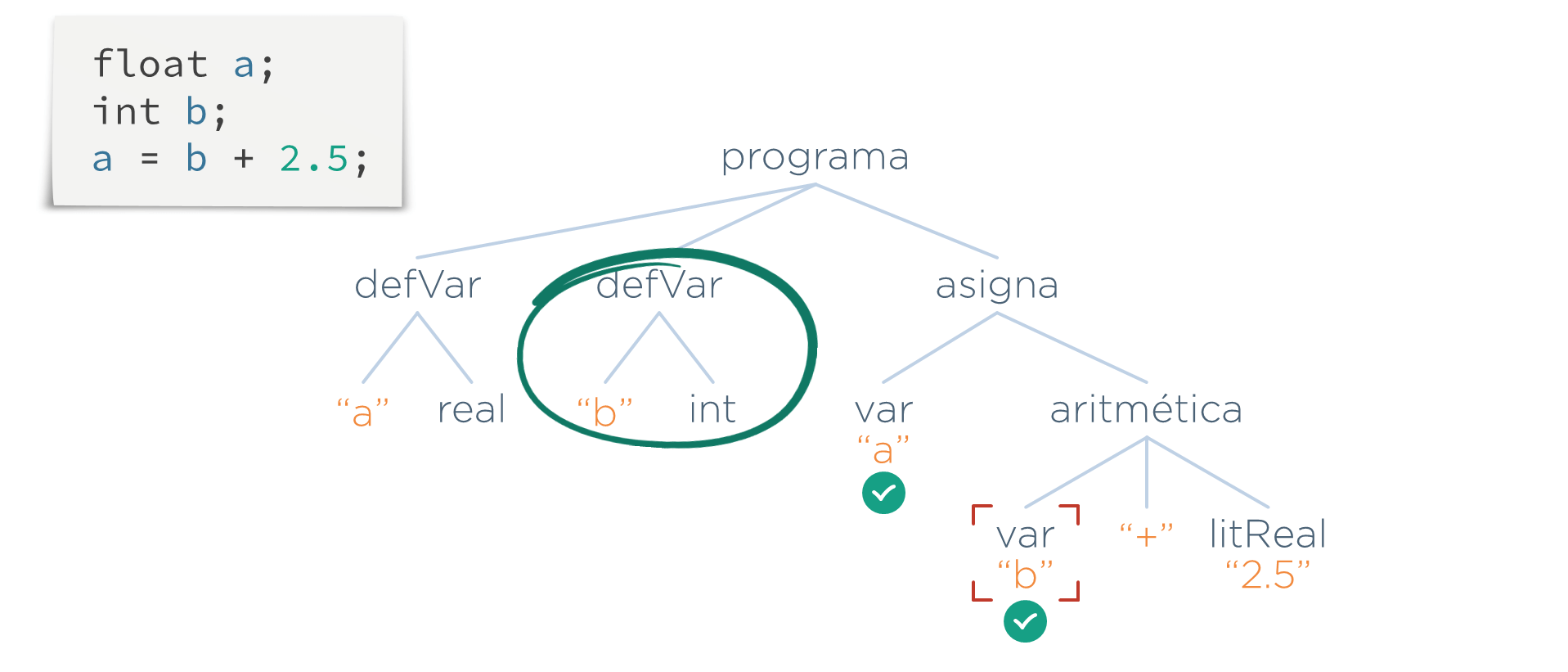
Una vez que se ha comprobado que todo símbolo ha sido definido, el programa quedaría validado por esta etapa.
Enlace de definiciones
- En esta etapa, además de comprobar que todo nodo var(n) tiene su defVar(n) hace algo más. Las fases posteriores necesitarán saber cómo se ha definido cada símbolo (tipo, ámbito…). Para que no tengan que repetir la búsqueda la definición del símbolo que ya se ha hecho aquí, esta etapa deja un enlace desde el símbolo a su definición
En el ejemplo anterior añadimos el enlace:
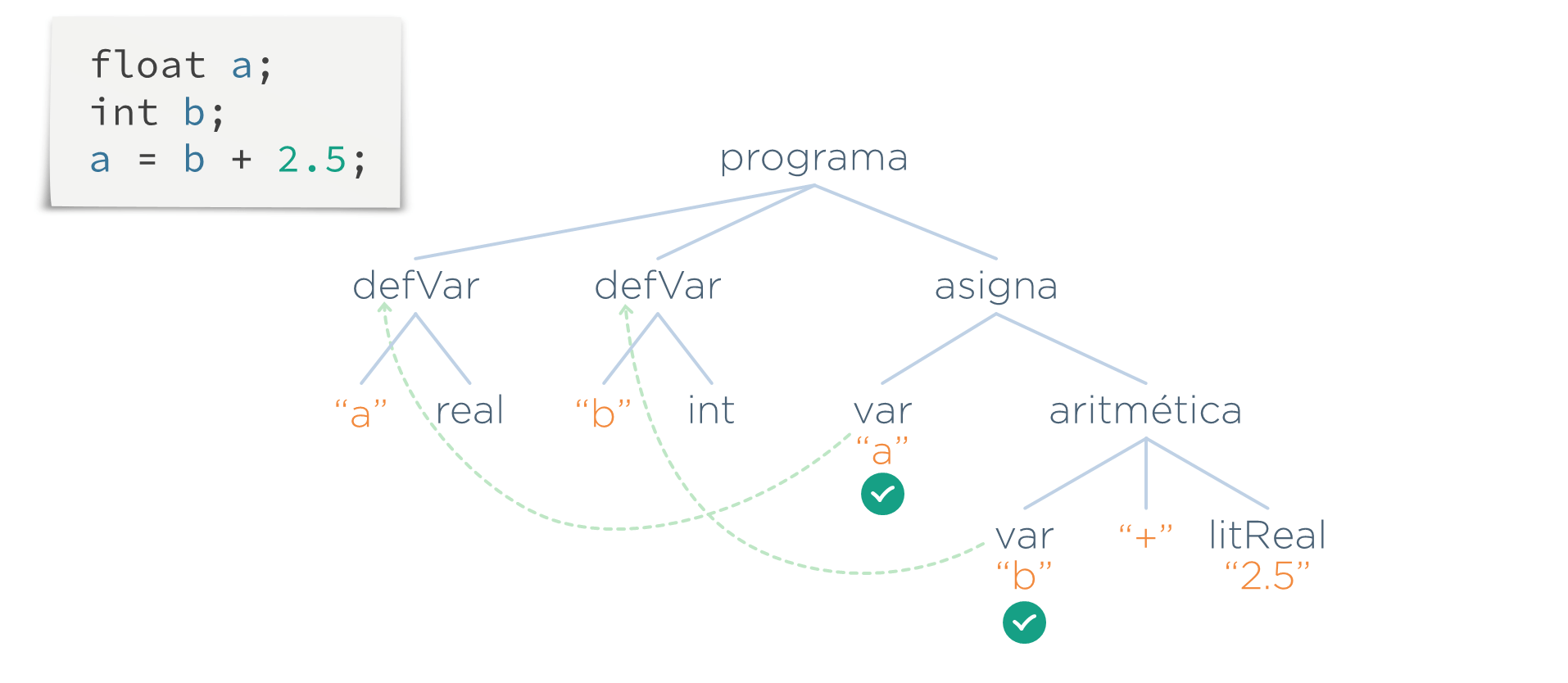
Etapa de Comprobación de Tipos
- Esta etapa se encarga de comprobar toda aquella situación relativa a los tipos. Algunos ejemplos de situaciones son:
- Operar tipos incompatibles
- Llamadas a funciones con un número o tipo erróneo en los argumentos
- Asignaciones a variables de valores incorrectos
Volviendo al ejemplo inicial:
print v[i] + 2;
De los cinco errores inicialmente indicados, esta etapa sería la que detectaría los tres últimos:
- Que i no fuera de tipo entero.
- Que v no fuera un array.
- Que
v[i]no fuera un tipo no numérico.
Predicados, atributos y funciones semánticas
Supóngase la siguiente programa entrada y su AST correspondiente:
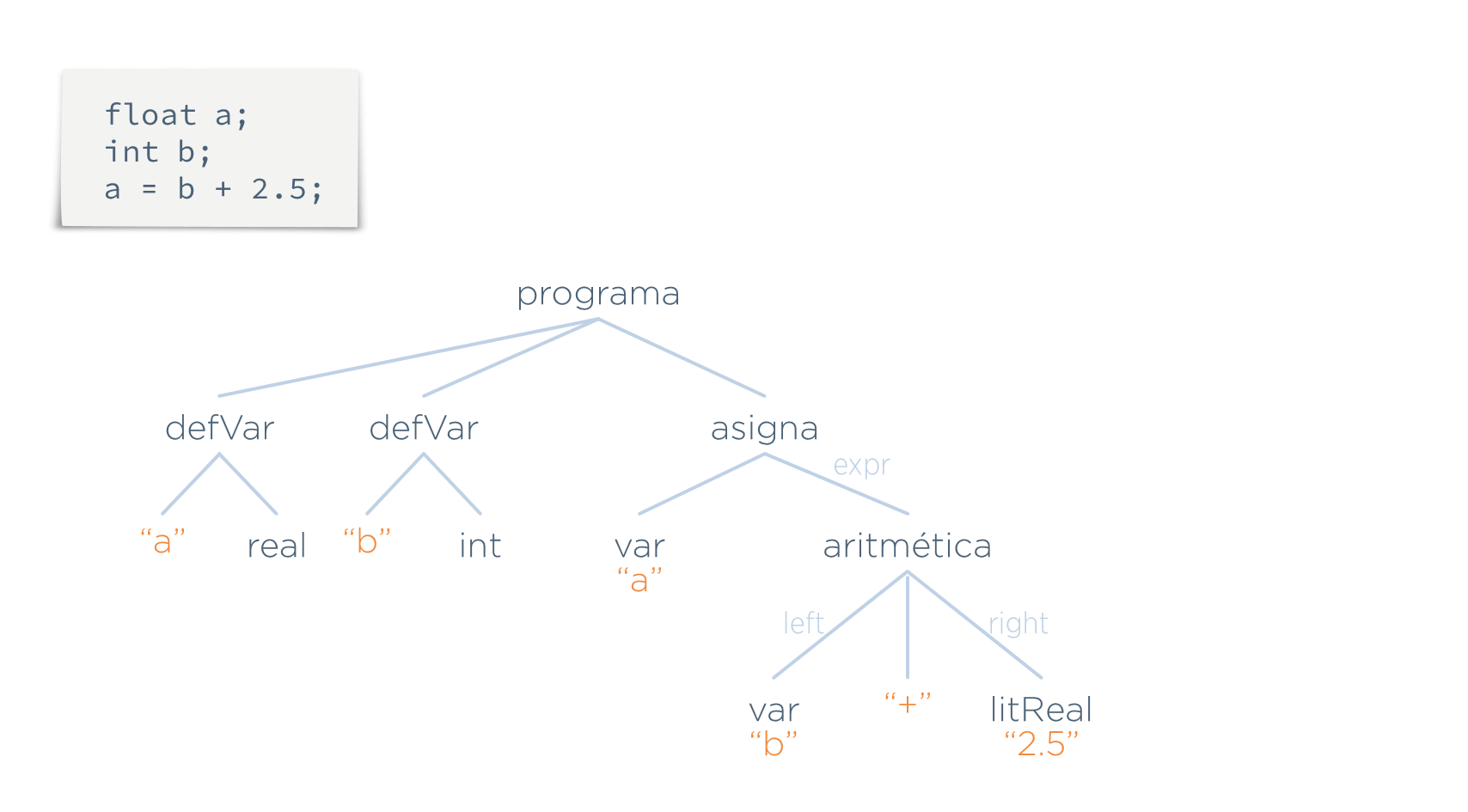
Para comprobar que las operaciones se están realizando con operandos del tipo adecuado, se asocian al AST predicados que detectan aquellas situaciones que no sean válidas. Son las condiciones que deben cumplir los nodos del árbol para que sean considerados válidos.
Supongamos que en este lenguaje hay dos normas:
- No se puede asignar un valor real a un entero
- Los operandos de una suma deben ser numéricos
Estas normas se reflejan mediante predicados que se asocian a ciertos nodos del árbol:
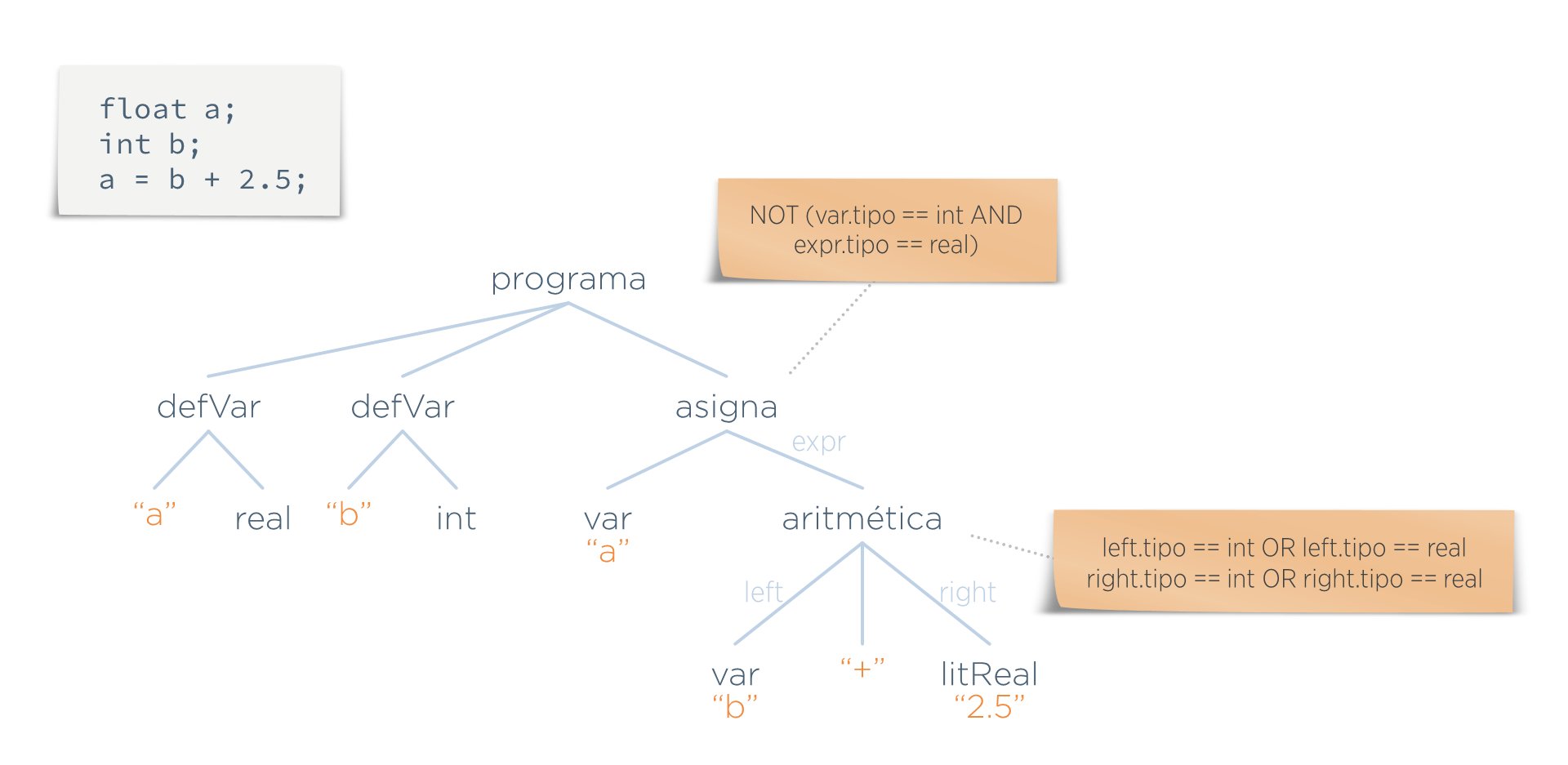
Pero esta etapa necesita algo más de información del AST, por lo que hay que añadirla. Esta información se la llama atributos. En este caso los atributos serían los 4 valores tipo añadidos a los nodos var, aritmetica y litReal:
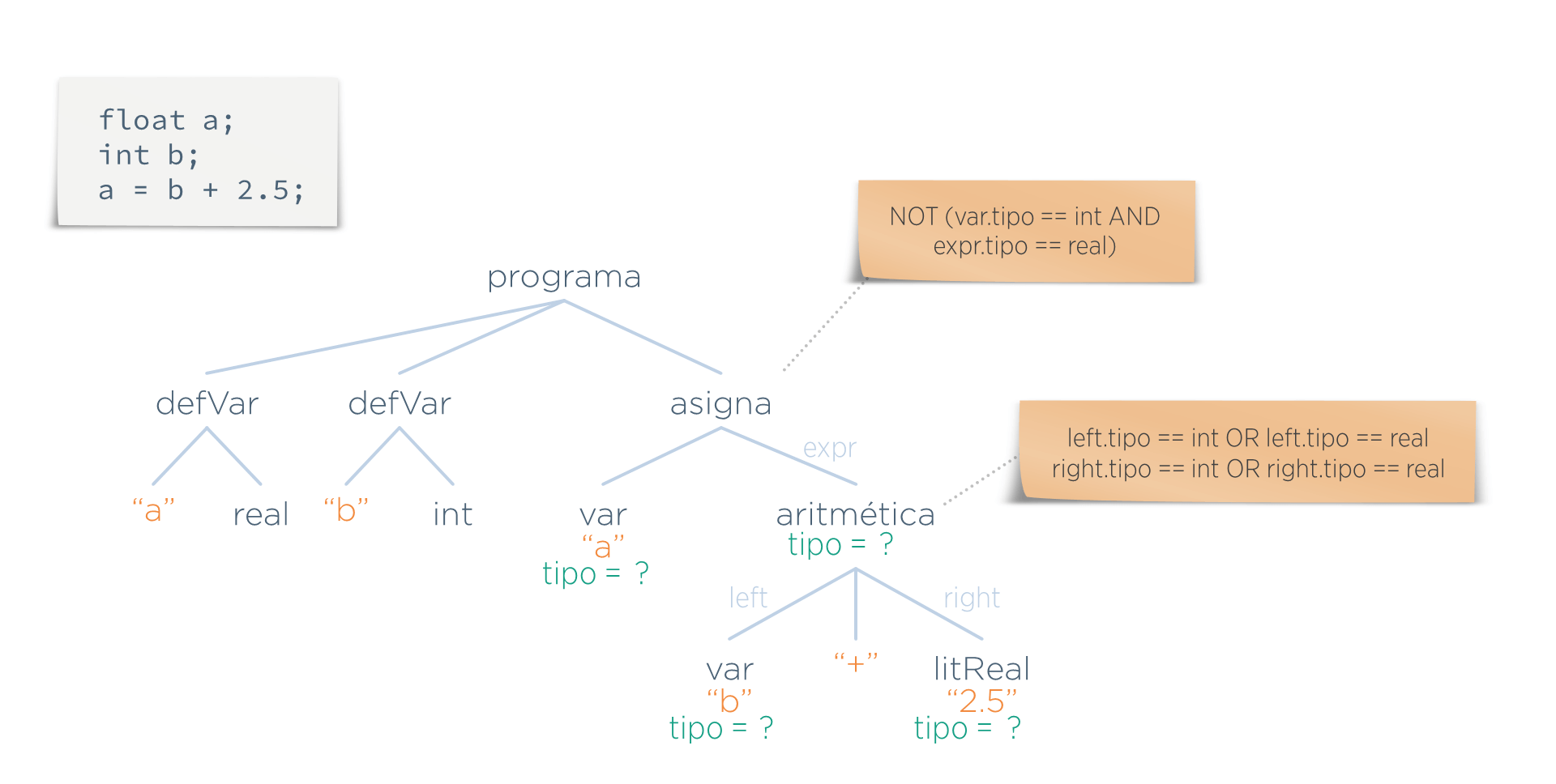
Para saber el valor de ese atributo están las funciones semánticas, que indican qué valor tiene que tomar cada atributo en cada nodo:
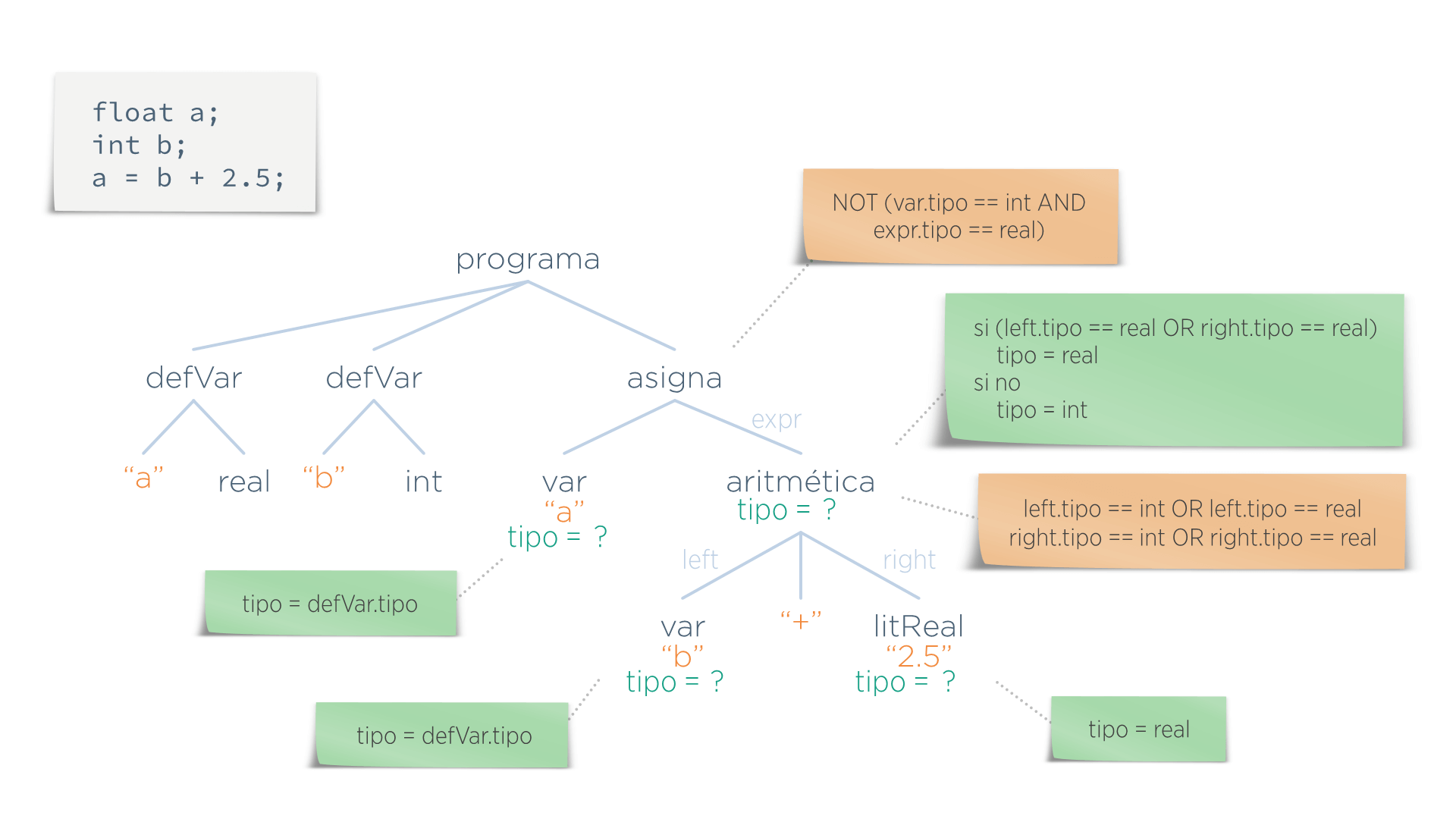
Interfaz del Analizador Semántico
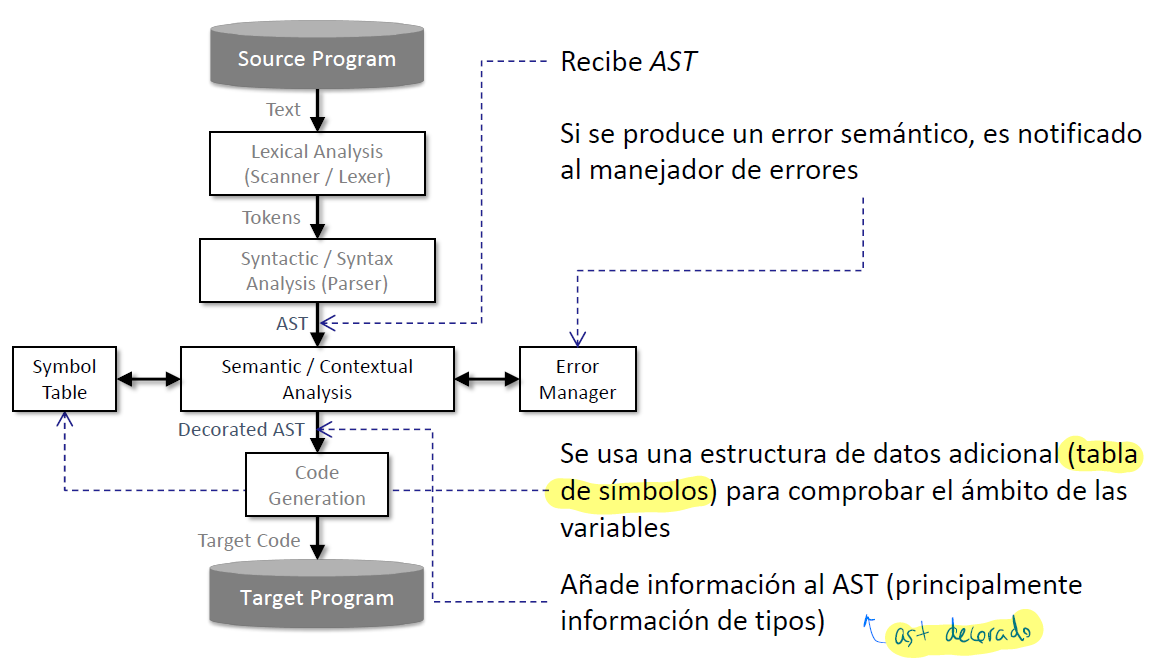
Comprobaciones semánticas
- Definición de variables y reglas de ámbito

- Unicidad: entidades que deberían ser únicas (enum, cases y switch)
- Enlaces: cuando el uso de una entidad debe vincularse a otra construcción (invocación de funciones)
- Comprobaciones pospuestas por el analizador sintáctico: l-value obligatorio en asignaciones, al menos una sentencia return en una función…
- Comprobaciones dinámicas: realizadas en tiempo de ejecución (accesos a arrays fuera de límites, comprobación de null)
- Comprobación de tipos: es la tarea más importante. Un analizador semántico debería:
- Inferir el tipo de las expresiones sintácticamente válidas
- Comprobar que las operaciones que se van a aplicar a una expresión son válidas respecto a su tipo
Anotación del AST
- Un analizador semántico verifica las reglas semánticas recorriendo un AST al que añade información adicional, recibiendo el nombre de AST decorado.
- Para decorar los AST vamos a usar gramáticas atribuidas (AG)
Gramáticas Libres de Contexto (CFG)
- Se usan para especificar la sintaxis de los lenguajes de programación. Sin embargo, no pueden representar la información adicional necesaria en las siguientes fases.


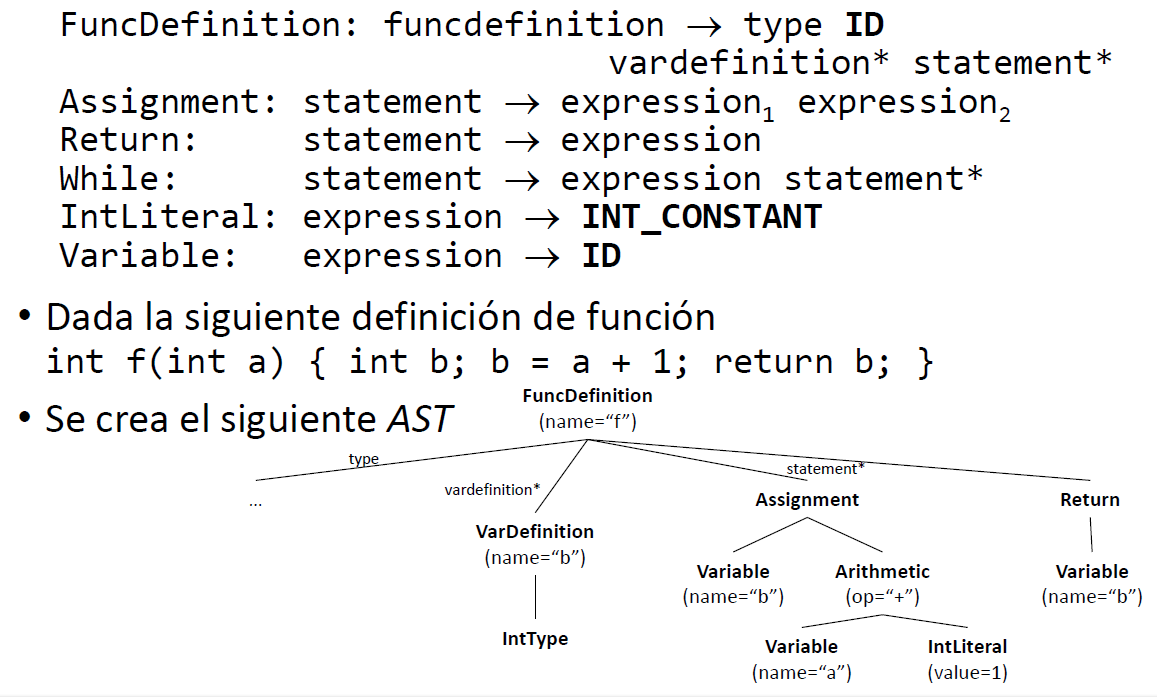



Ejemplo de AG
Dada la siguiente gramática abstracta: (G):

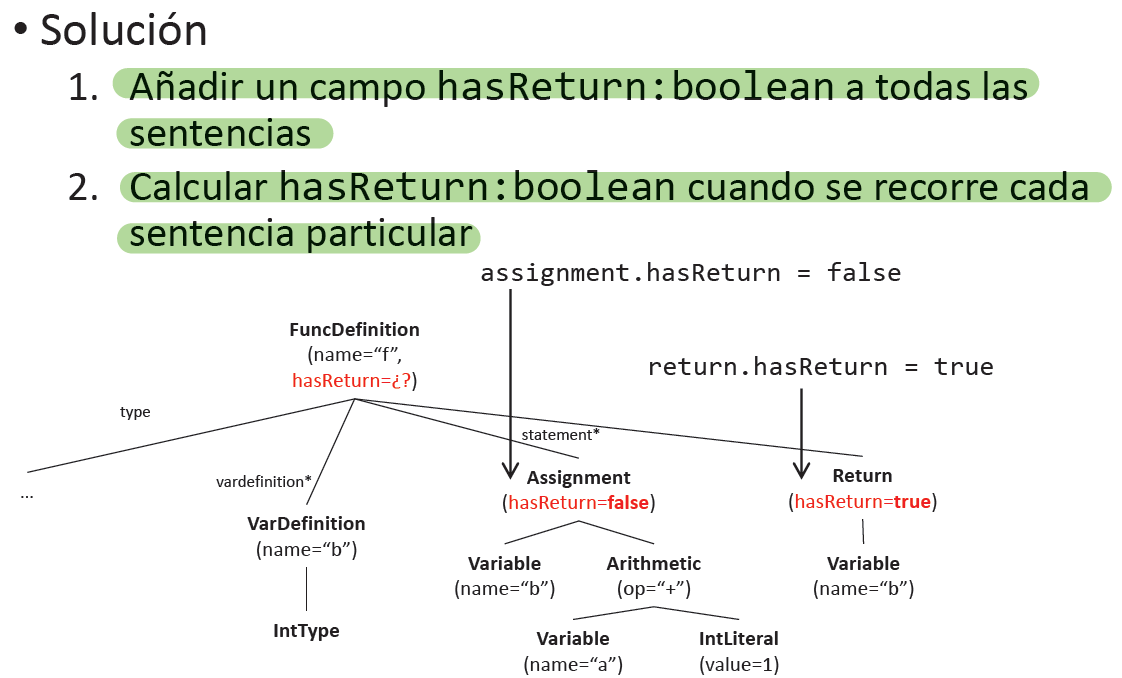
- Añadimosun atributo booleano hasReturn a los símbolos de la gramática funcdefinition y statement
- Calculamos sus valores mediante reglas semánticas
Definir una AG:
(A):
{funcdefinition.hasReturn, statement.hasReturn}
(R):
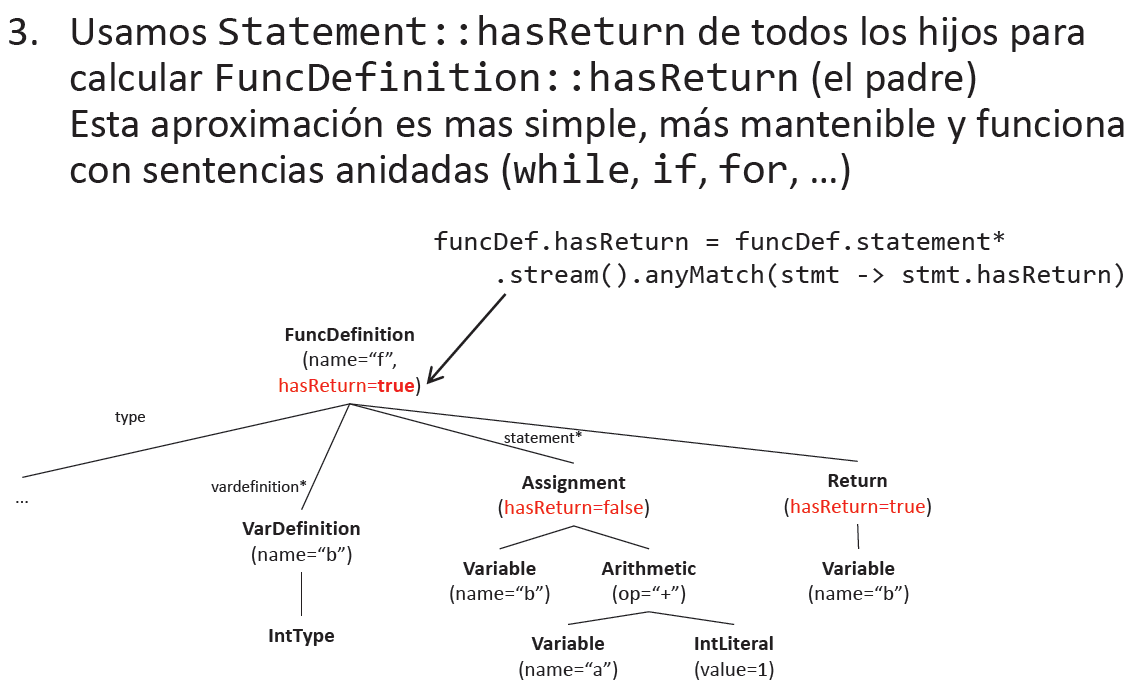
(1) funcdefinition.hasReturn = statement.stream().anyMatch(stmt -> stmt.hasReturn)
(2) statement.hasReturn = false
(3) statement.hasReturn = true
(4) statement.hasReturn = statement.stream().anyMatch(stmt -> stmt.hasReturn)Gramáticas atribuidas
- Las gramáticas atribuidas añaden atributos a las construcciones sintácticas de un lenguaje
- Las AG especifican, de forma declarativa, cómo se calculan los valores de los atributos
Atributos
- Un atributo es una propiedad de una construcción sintáctica.
- Para cada atributo, su dominio debe ser especificado (ej: type debe ser int, char o double)
- Cuando un símbolo aparece más de una vez en una producción, se usan sufijos para referirse sin ambigüedades a sus atributos
- Atributos MÁS comunes:
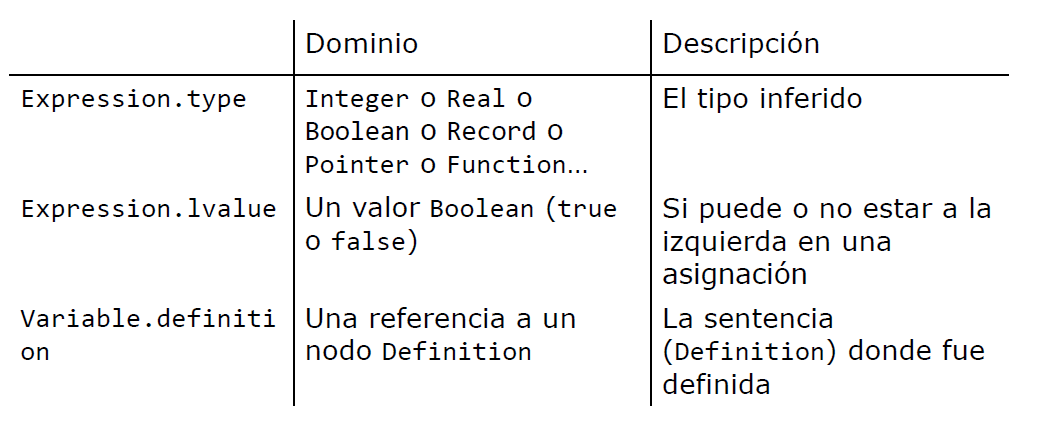
Reglas semánticas
- Especifican cómo se calcula un atributo de un símbolo a partir de los atributos de otros símbolos en la misma producción
Evaluación de las gramáticas atribuidas
- Cálculo de todos los atributos de un programa dado.
- Precisa calcular el orden de ejecución de las reglas semánticas
Algoritmo general para la evaluación de las AGs:
- Contruir el árbol de sintaxis para un programa específico
- Crear el grafo de dependencias de atributos
- Calcular un ordenamiento topológico del grafo dirigido
- Ejecutar las reglas semánticas, siguiendo dicho ordenamiento topológico
Gramáticas bien definidas
- Una AG está bien definida (no circular) si, para cada árbol sintáctico, pueden ser evaluados todos los atributos

Atributos sintetizados
- Para evaluar las AGs usaremos AGs donde los atributos de los nodos padres dependen de los atributos de los nodos hijos (conocidos como atributos sintetizados)
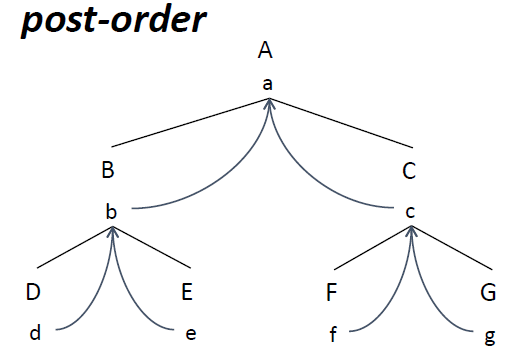
Atributos heredados
- Se asigna un valor a los atributos de los nodos hijos


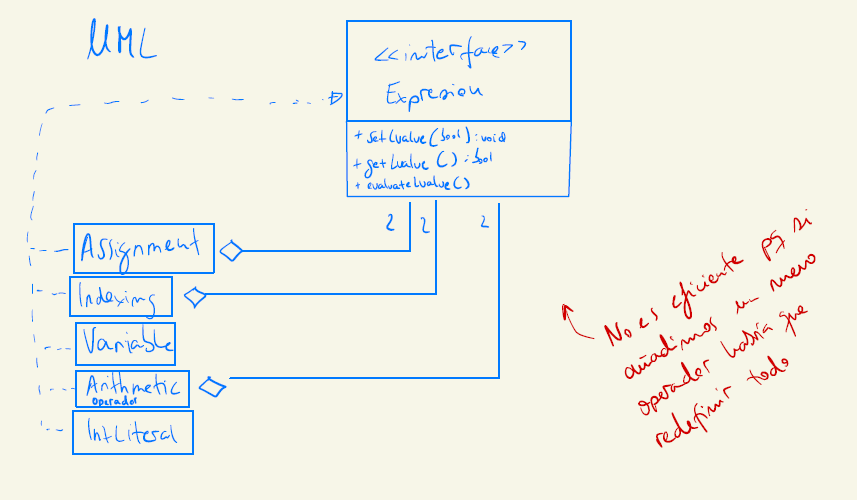
Patrón Visitor
- Para recorrer el ast con un visitor, llamaremos al método accept (y dentro de este sí podemos llamar a un visit)
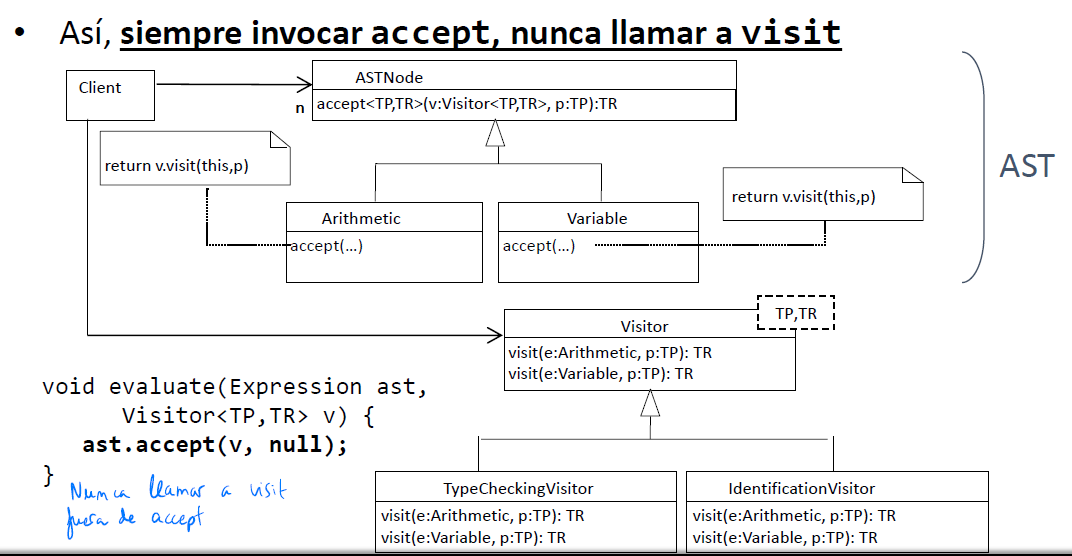
Tipo de las variables
- Debe ser indicado en su definición en los lenguajes con declaración explícita de tipos

- Por lo tanto, tenemos que almacenar el tipo de una variable en su definición (varDefinition)
- Su tipo de puede consultar posteriormente cuando se utiliza la Variable (nodo Variable)
- Por lo tanto, el nodo Variable estará enlazado a (decorado con) su correspondiente nodo varDefinition
- Este trabajo lo realiza la fase de Identificación
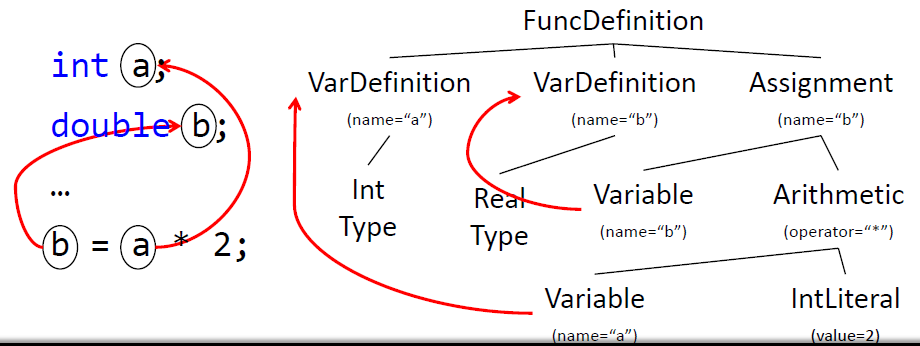
Tabla de Símbolos
- Estructura de datos temporal donde se almacenan los nodos VarDefinition para permitir su posterior recuperación
- Una vez que los nodos Variable están vinculados a las VarDefinitions correspondientes, la tabla de símbolos se puede eliminar
Ámbito de las variables
- El ámbito es la parte de un programa donde el nombre de una variable está vinculado a una entidad
- global o local
Comprobación de tipo
- Las reglas semánticas relacionadas con la comprobación de tipos son de las más importantes (ej:
[]sólo se puede usar en arrays) - Si la regla no se cumple se produce un error de tipo
- La comprobación de tipo consta de las siguientes dos tareas:
- Debe inferirse el tipo de cada subexpresión
- Debe verificarse que sean válidas las operaciones acplicadas a cada subexpresión respectivamente
Fase de compilación
- Aunque la comprobación de tipos y la identificación se pueden realizar en la misma pasada, separarlos en diferentes recorridos normalmente produce un código más fácil de mantener
- La fase de identificación se realiza antes de la de comprobación de tipos
- Por lo tanto, el recorrido de comprobación de tipos puede confiar en el enlace existente entre cada nodo Variable y su correspondiente Definition (a través del atributo definition)
Definición de tipo
- Los tipos suelen ser definidos desde 3 puntos de vista diferentes:
- Denotacional: conjunto de valores
- Basado en abstracción: es una interfaz con operaciones
- Constructivo:
- built-in: tipos primitivos
- compuesto aplicando un constructor de tipos (astruct, array, puntero…)
Expresión de tipo
- Es la representación de un tipo
- Se basan en la definición constructiva de tipo
- Una expresión de tipo es:
- Un tipo básico (built-in) (int, char, double…)
- O un tipo compuesto creado aplicando un constructor de tipo (array…) a otras expresiones de tipo (array(int)…)
Sistema de Tipos
- Colección de reglas para asignar expresiones de tipo a las diferentes construcciones sintácticas del lenguaje
- Un comprobador de tipos implementa un sistema de tipos y es parte del analizador semántico
- Las gramáticas atribuidas proporcionan un mecanismo para especificar sistemas de tipos
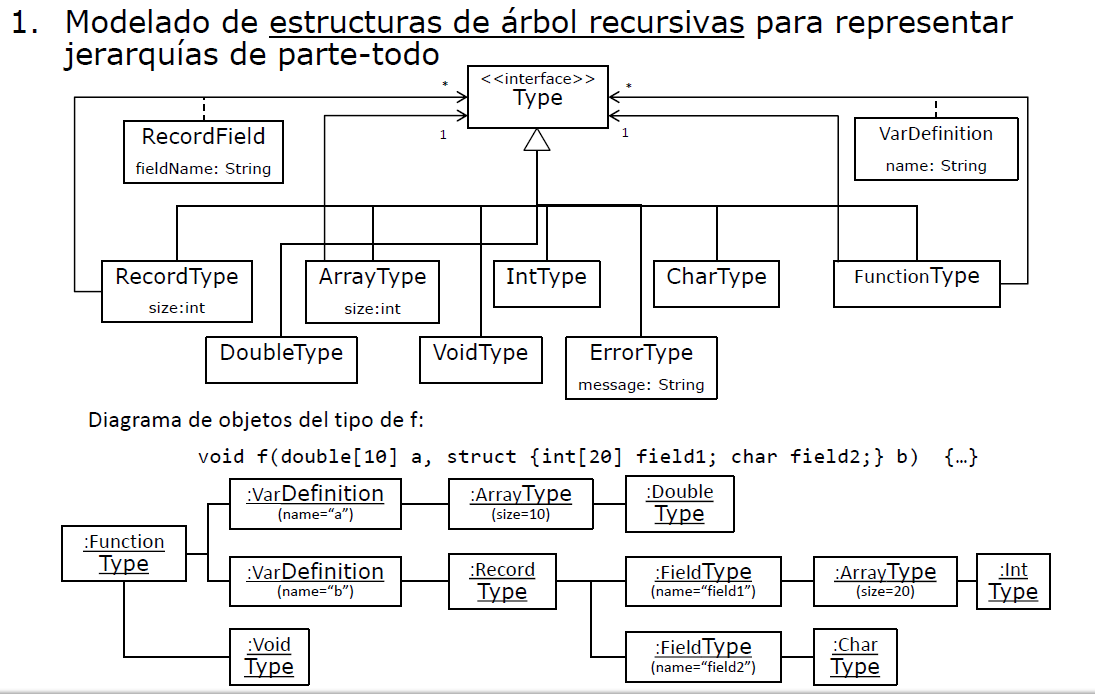
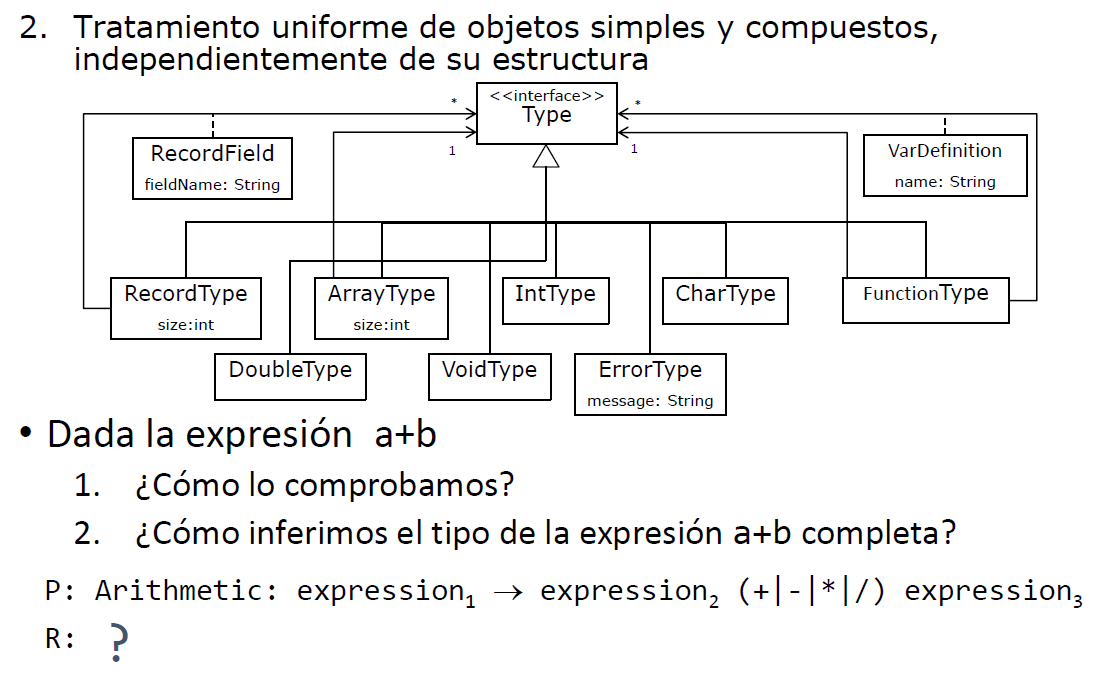
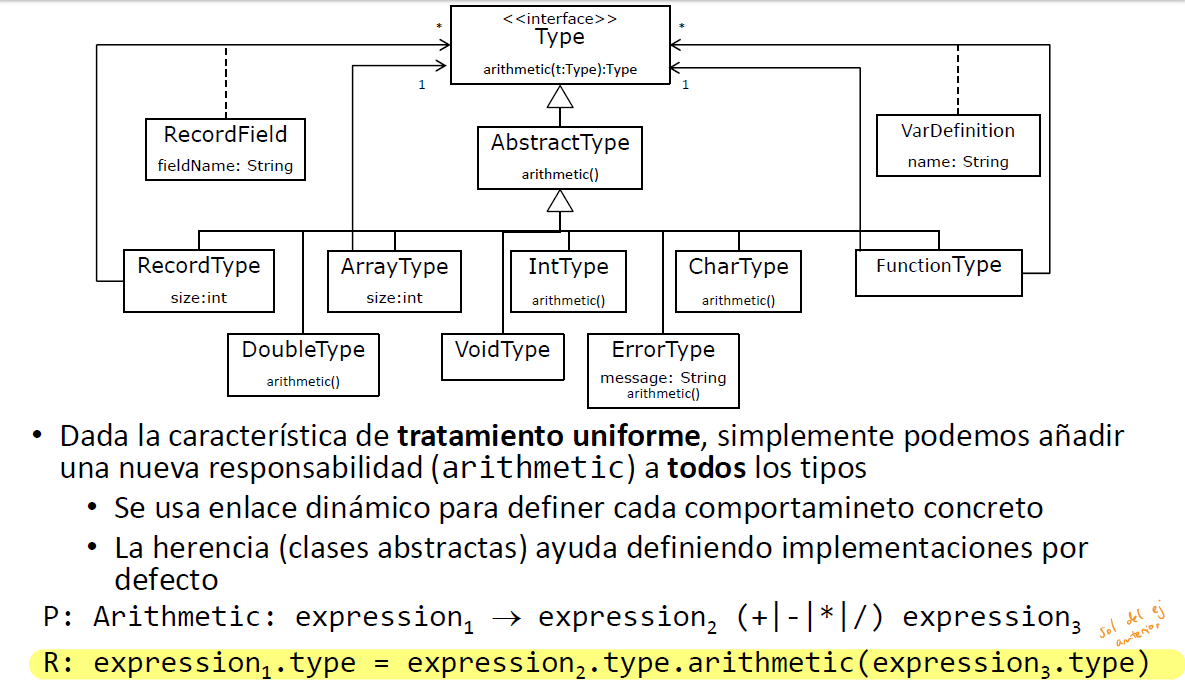
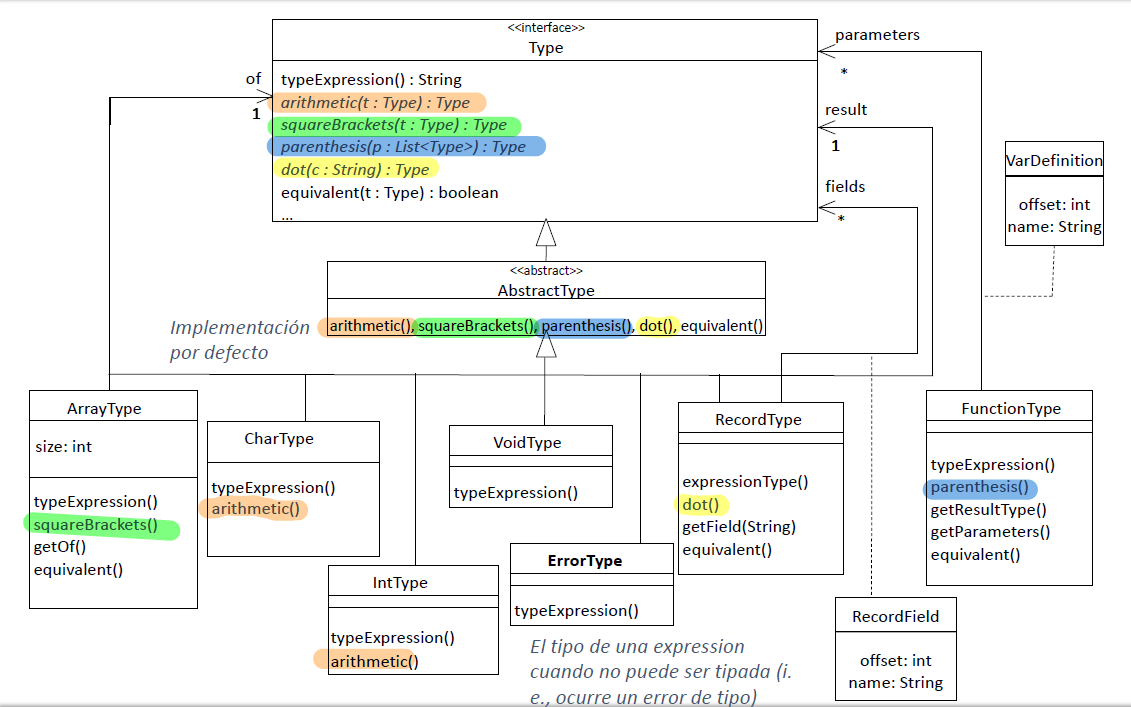
Patrón Composite
Anotación para resolver el ejercicio 6 de Semántico → Semántico

Mirar ejercicios en Semántico
Lenguajes y representaciones intermedias
Hay:
- De alto nivel
- De medio nivel
- De bajo nivel
MAPL: Arquitectura
MAPL es una representación intermedia de Medio nivel.
- IP, Instruction Pointer: dirección de la instrucción en ejecución
- SP, Stack Pointer: dirección del tope de la pila
- BP, Base Pointer: dirección del marco de pila activo
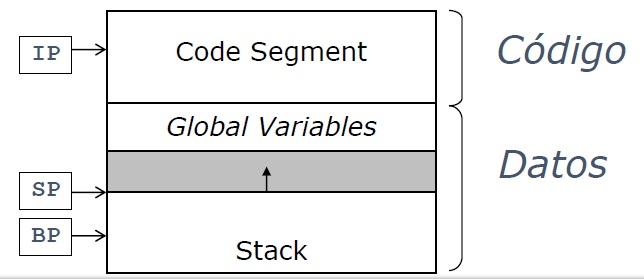
MAPL: Instrucciones push y pop

MAPL: Instrucciones load

MAPL: Instrucciones store

MAPL: Operaciones

MAPL: I/0 y Conversiones

Ver ejercicios en Generación de código
Generación de código
Los principales subproblemas de la generación de código son:
- Asignación del almacenamiento
- Selección de instrucciones
- Asignación de registros
Entornos de ejecución
- Un compilador debe:
- Asignar estáticamente la dirección de memoria que tendrá cualquier variable en tiempo de ejecución (ha de hacerlo en tiempo de compilación)
- Generar código que gestione la organización de la memoria en tiempo de ejecución y mantenga la información para guiar el proceso de ejecución
Símbolos y tipos
- Los símbolos (Variable) en el análisis semántico se enlazan a sus definiciones para inferir sus tipos (fase de identificación). En la generación de código se utilizan para conocer las direcciones de memoria de las variables
- Los tipos en el análisis semántico se utilizan para verificar la validez de algunas construcciones sintácticas. En la generación de código incorporan el tamaño y la representación de cada variable
Tipos


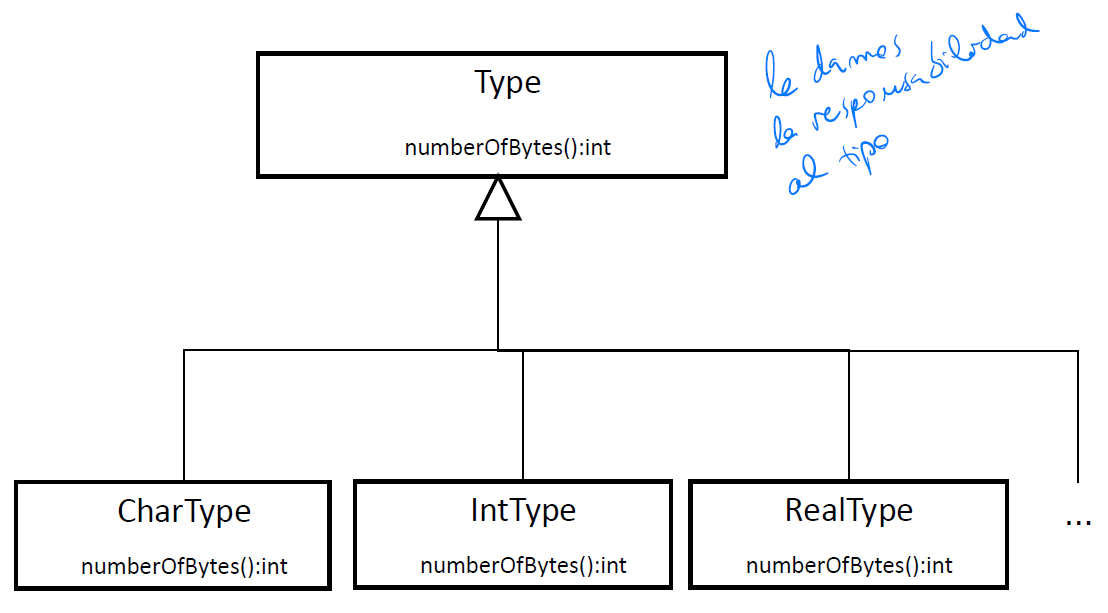
El número de bytes para almacenar un array es la multiplicación de su tamaño y el número de bytes del tipo de sus elementos.
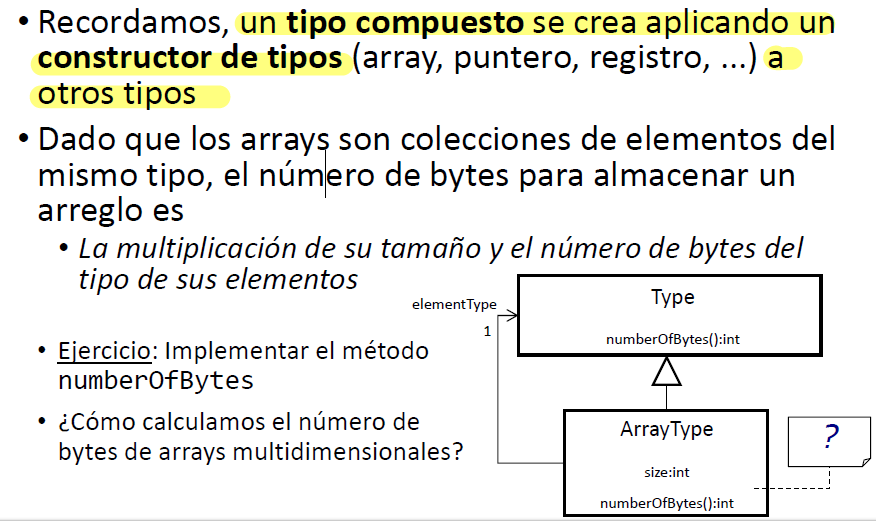
public int numberOfBytes(){
return size*elementType.numberOfBytes();
}Tipos Compuestos: Structs
- Un registro (struct) es una colección de campos de diferentes tipos donde cada campo se identifica por su nombre
- El tamaño de un registro es la suma de los tamaños de los tipos de los campos
- El desplazamiento (offset) de memoria relativo de cada campo es la suma de los tipos de los campos anteriores
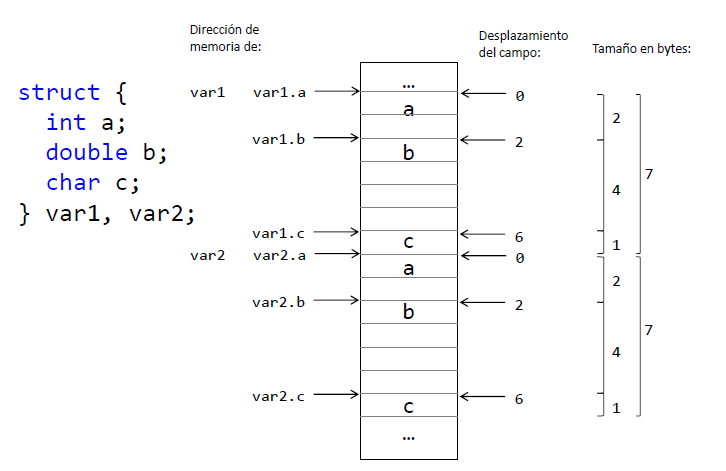
Memoria estática
- El tamaño de la memoria estática permanece fijo durante la ejecución del programa
- La memoria estática se divide en áreas de código y datos
- El tamaño del área de datos en la memoria estática permanece fijo durante todo el proceso de ejecución
- Normalmente se accede a los datos estáticos por sus direcciones de memoria absolutas
- Los datos comunres incluídos en la memoria estática son:

- En MAPL los datos estáticos tienen direcciones de memoria crecientes, comenzando en cero
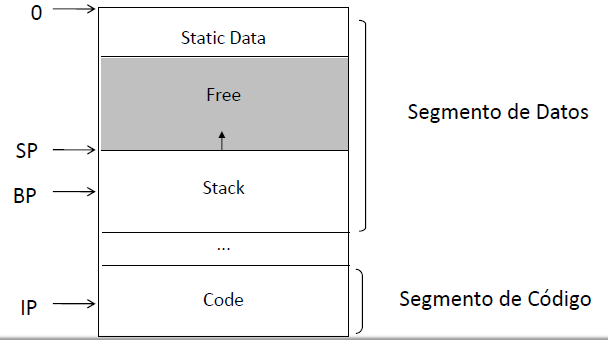
Plantillas de código
- Se basan en semántica denotacional (formalizar el significado de una construcción sintáctica describiendo el efecto de ejecutarla)

Elementos de una plantilla de código

Generación de código Inductiva

Escribiendo el código generado

Contexto

Parametrización de plantillas. Alternativa 1


Parametrización de plantillas. Alternativa 2

- Las funciones de código que se usan son address, value y execute:


Funciones de código
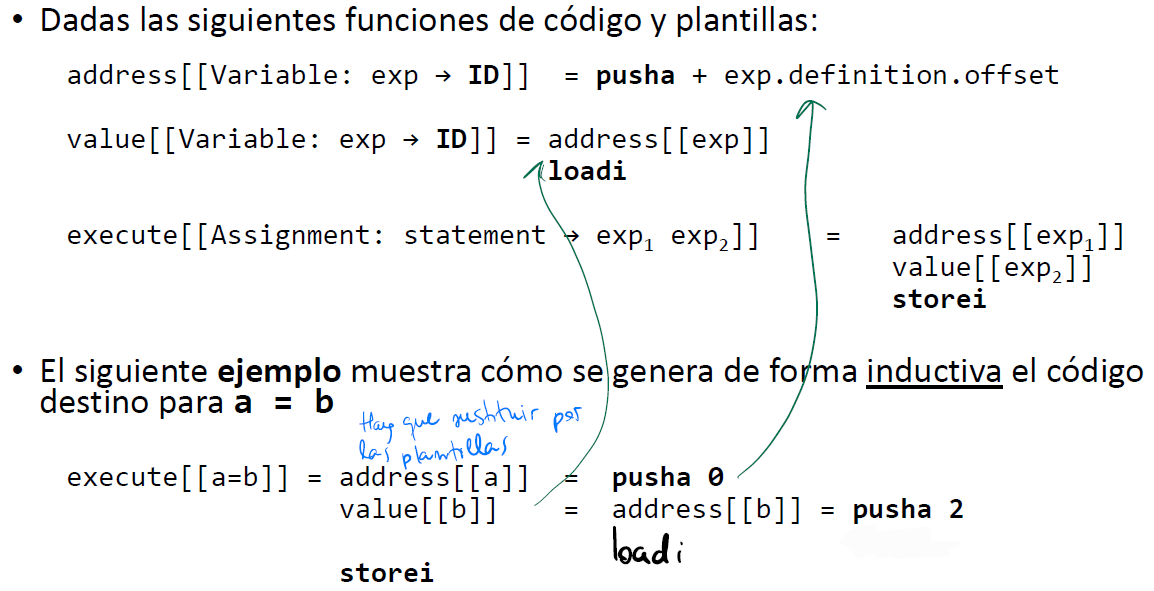
Definiciones de funciones de código


Implementación típica: usar 3 visitors → ExecuteCGVisitor, ValueCGVisitor, AddressVisitor

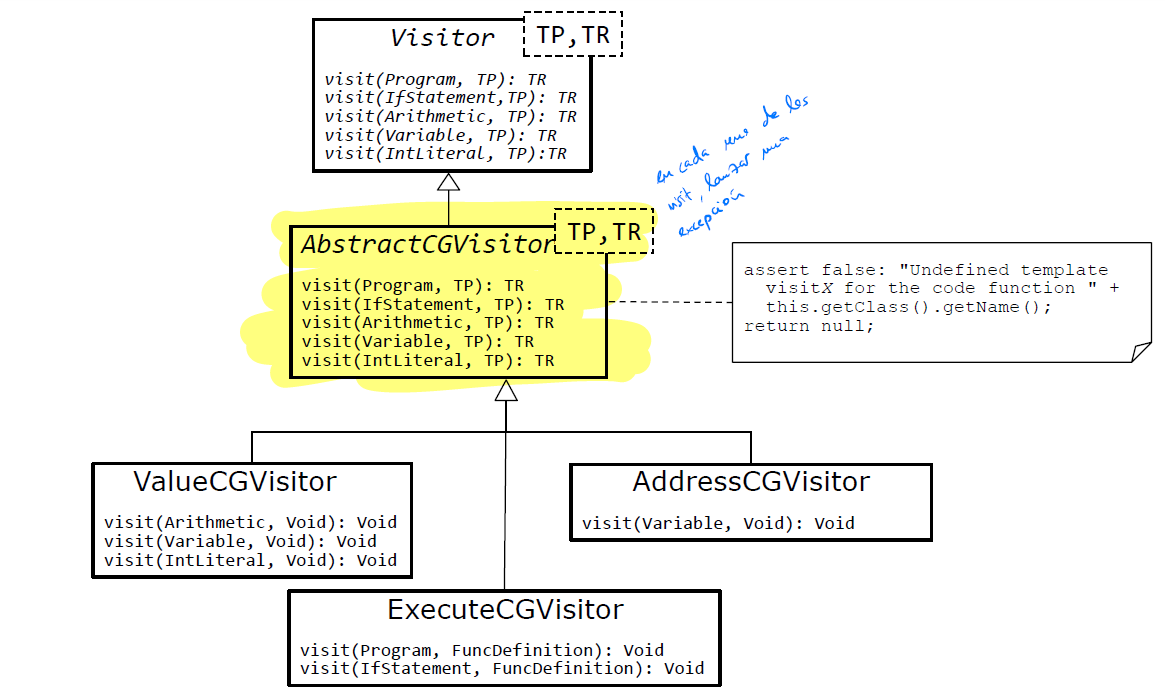
Generación de código de estructuras de datos: Definición de variable

Generación de código de estructuras de datos: Definición de variable Local

Generación de código de estructuras de datos: Expresiones



Generación de código de estructuras de datos: Arrays
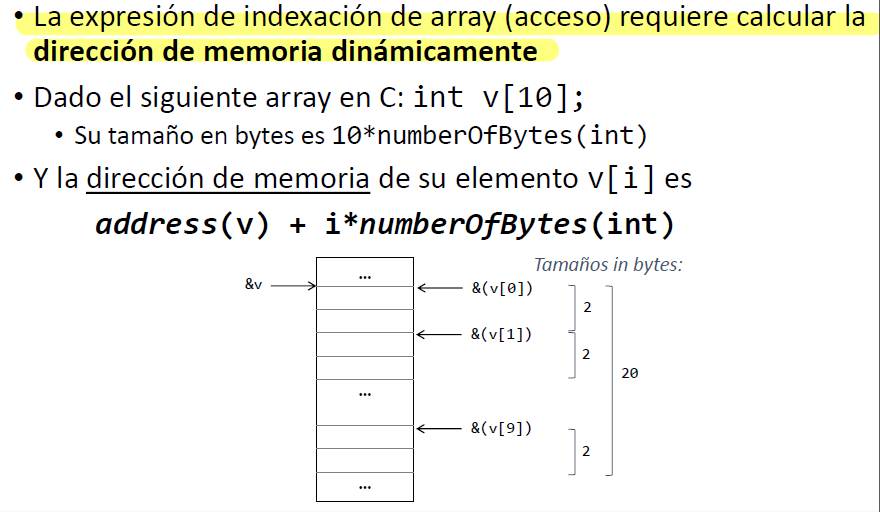


Generación de código de estructuras de datos: Registros


Sentencias de control de flujo. Etiquetas y saltos

While
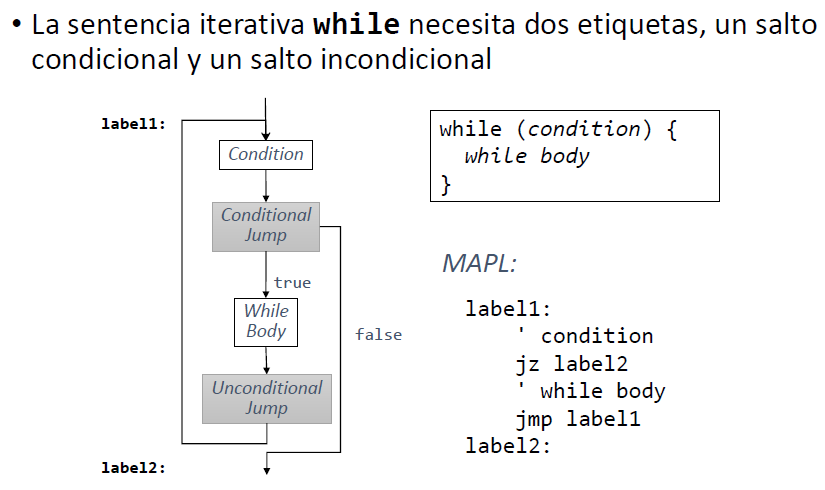
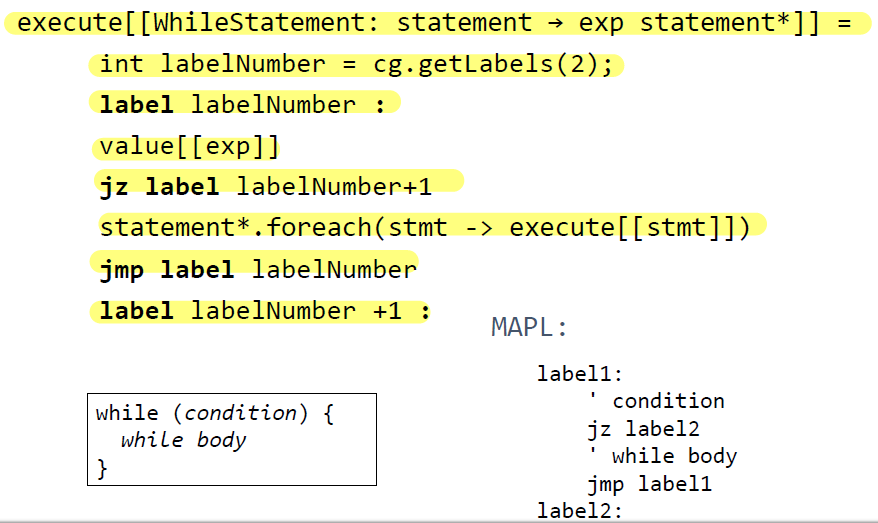
Do while
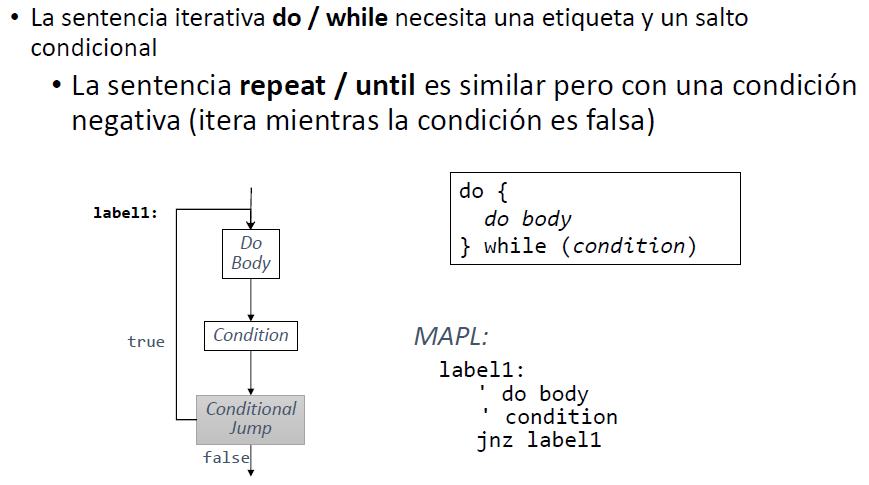

For


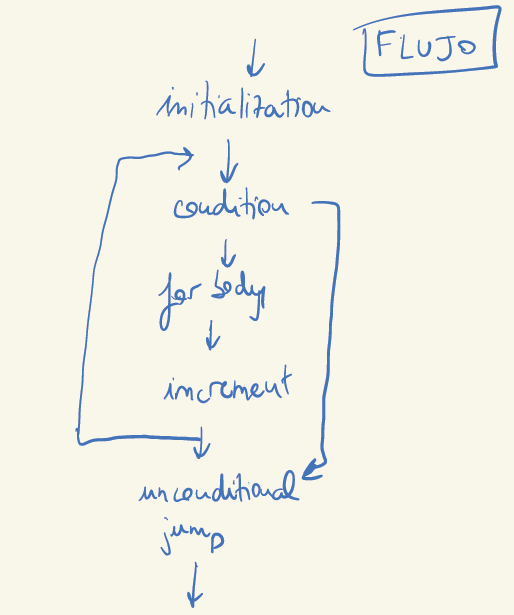
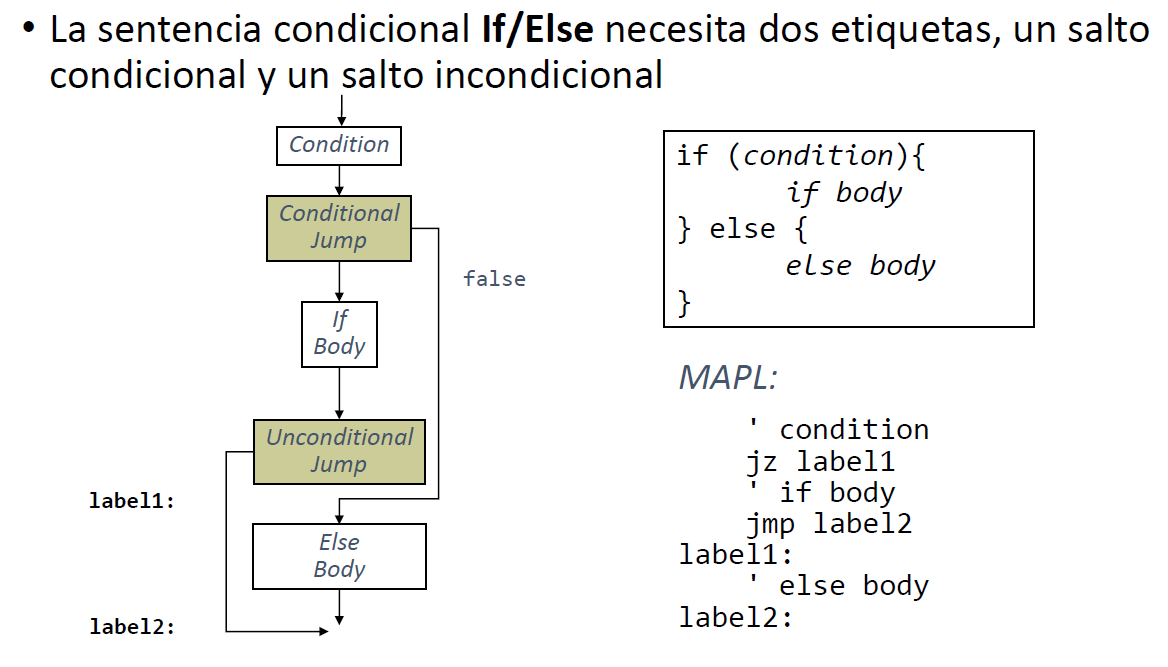
If/else

Funciones/Procedimientos




