Ejercicios y apuntes para Examen Teoría ED 🍑

Note

En este documento están todos los ejercicios de seminario resueltos y hay algunas definiciones que considero interesantes para el examen de teoría

Tip

Te recomiendo que veas los siguientes archivos:

• Exámenes de Teoría ED 🍅
• Notas de Laboratorio ED 🍄
• Seminarios ED 🚗

Seminario 2. Grafos

Dijkstra

• Algoritmo de caminos mínimos
• Objetivo: determinar el camino más corto desde el nodo origen al resto de los nodos del grafo
• Aplicaciones:
  • Encadenamiento de paquetes por los routers
  • Reconocimiento del lenguaje hablado
  • Enrutamiento de aviones y tráfico aéreo

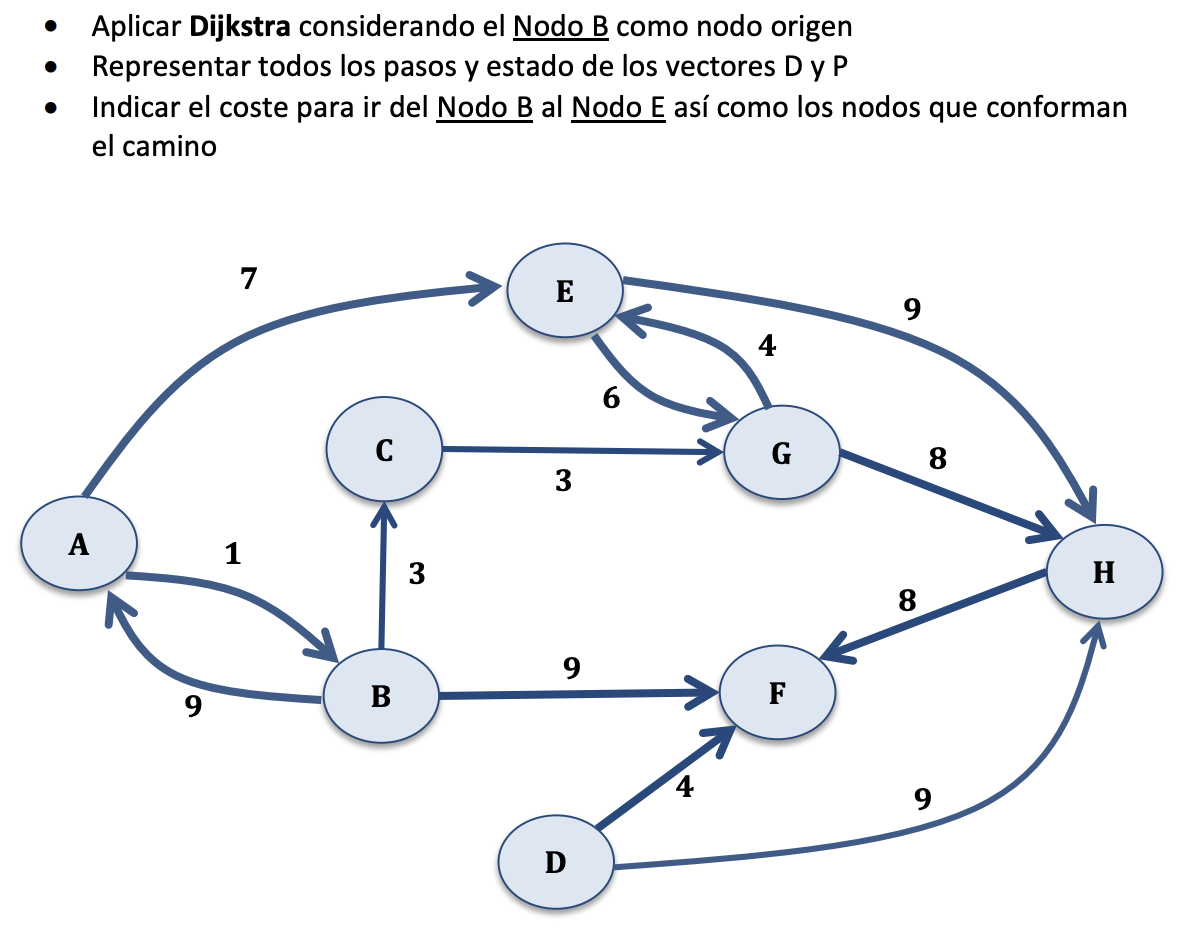
Dijkstra. Ejercicio 1

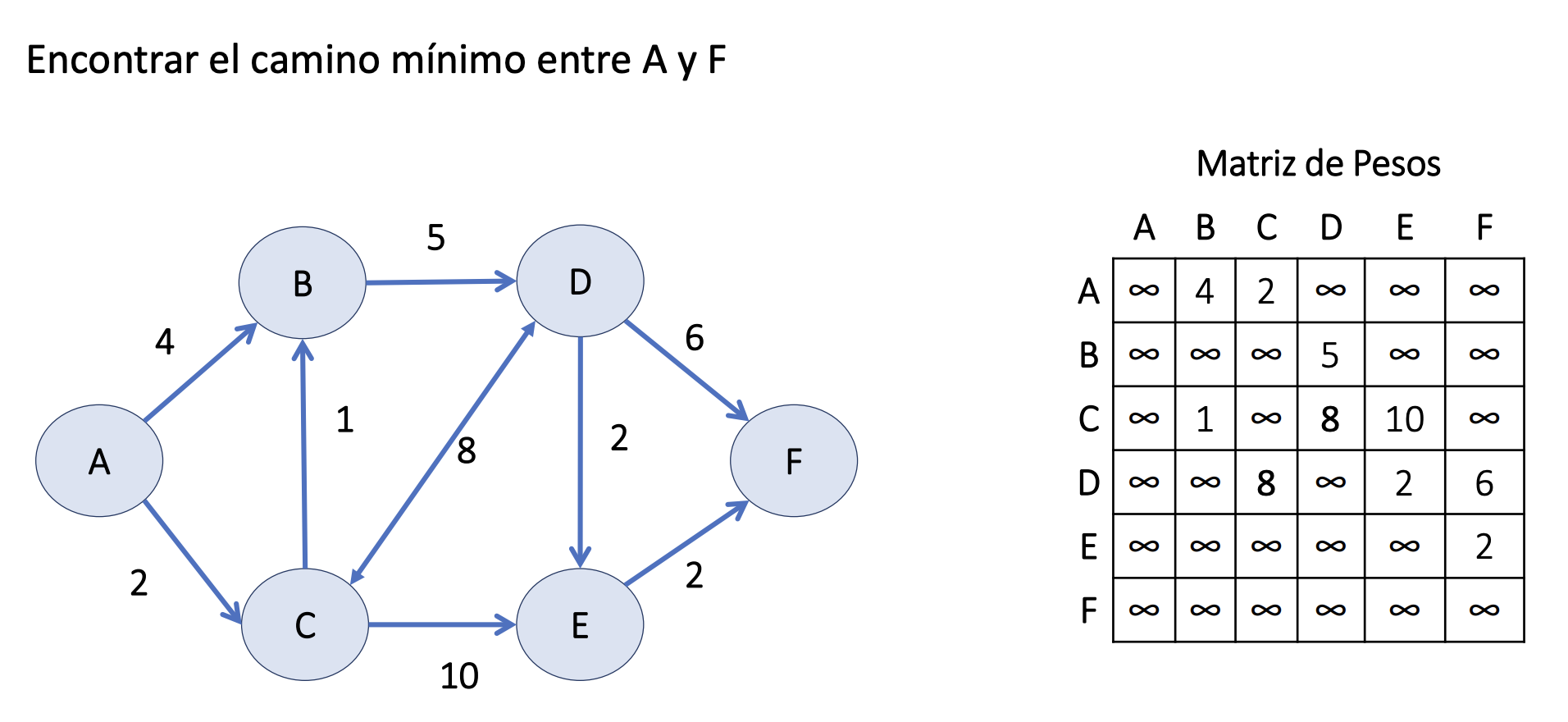
Dijkstra. Ejercicio 2

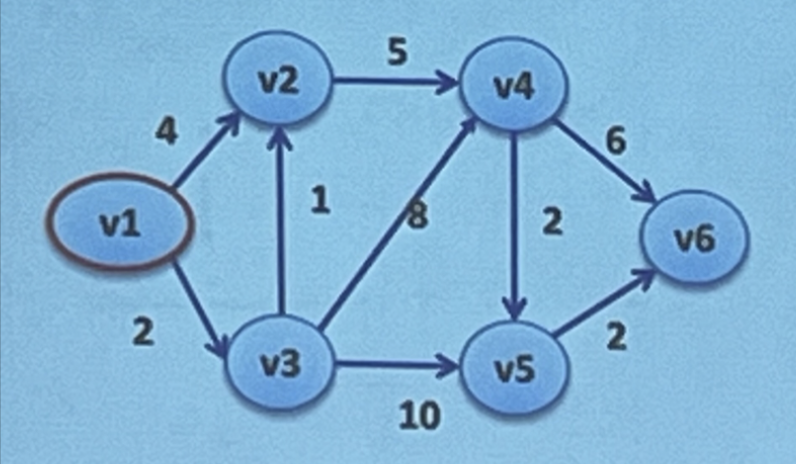
Dijkstra. Ejercicio 3

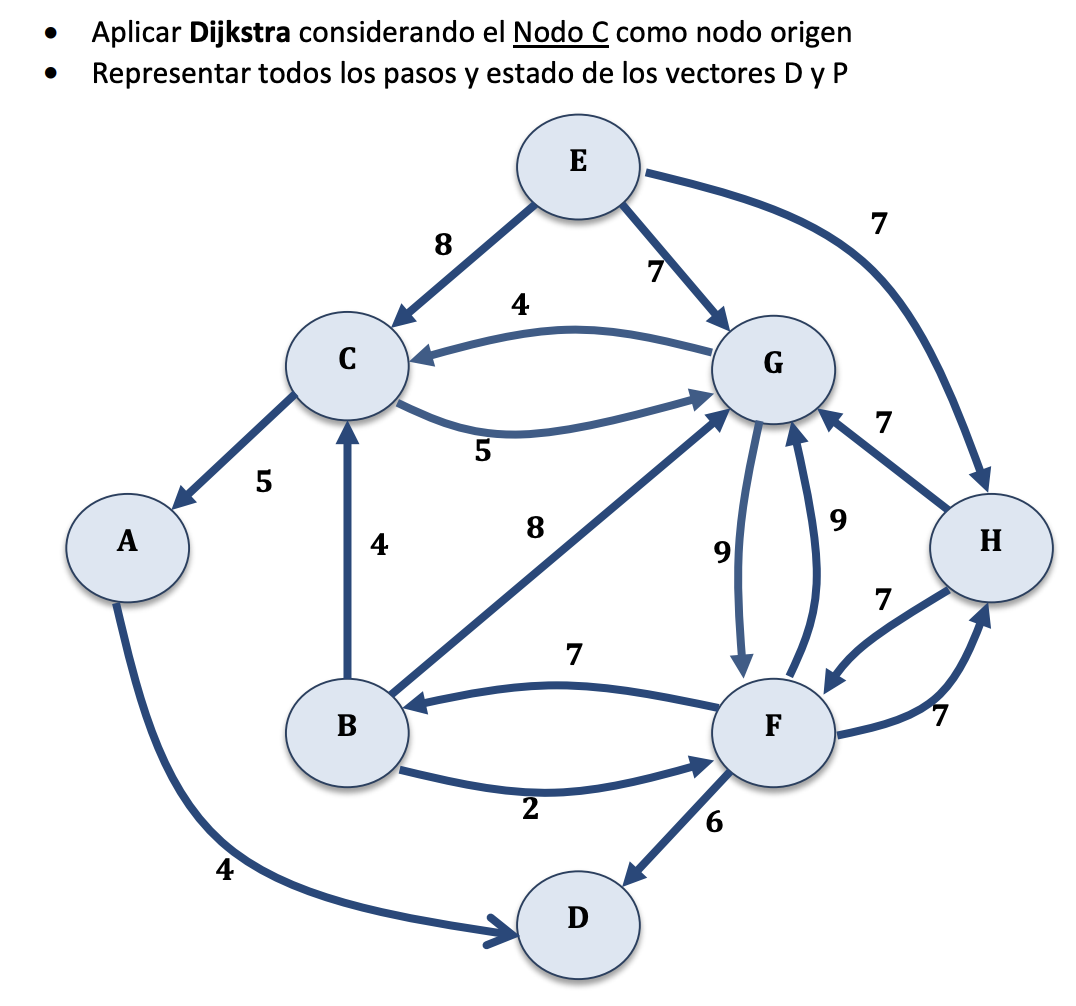
Dijkstra. Ejercicio 4

Seminario 3. Grafos

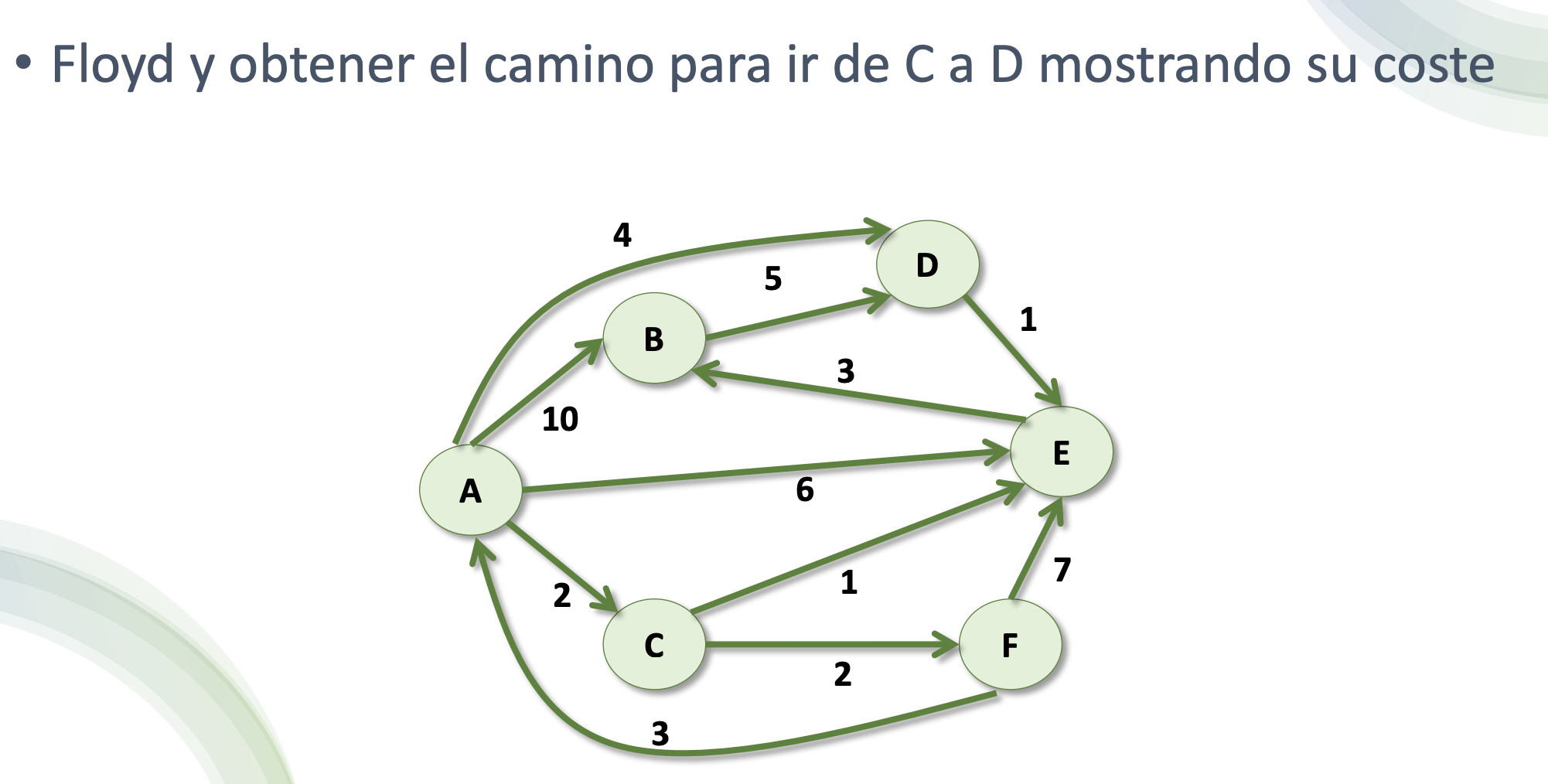
Floyd-Warshall

• Algoritmo que calcula todos los caminos de coste mínimo entre cualquier par de nodos del grafo
• Características del grafo:
  • Ponderado
  • Conexo
  • Dirigido

Floyd-Warshall. Ejercicio 1

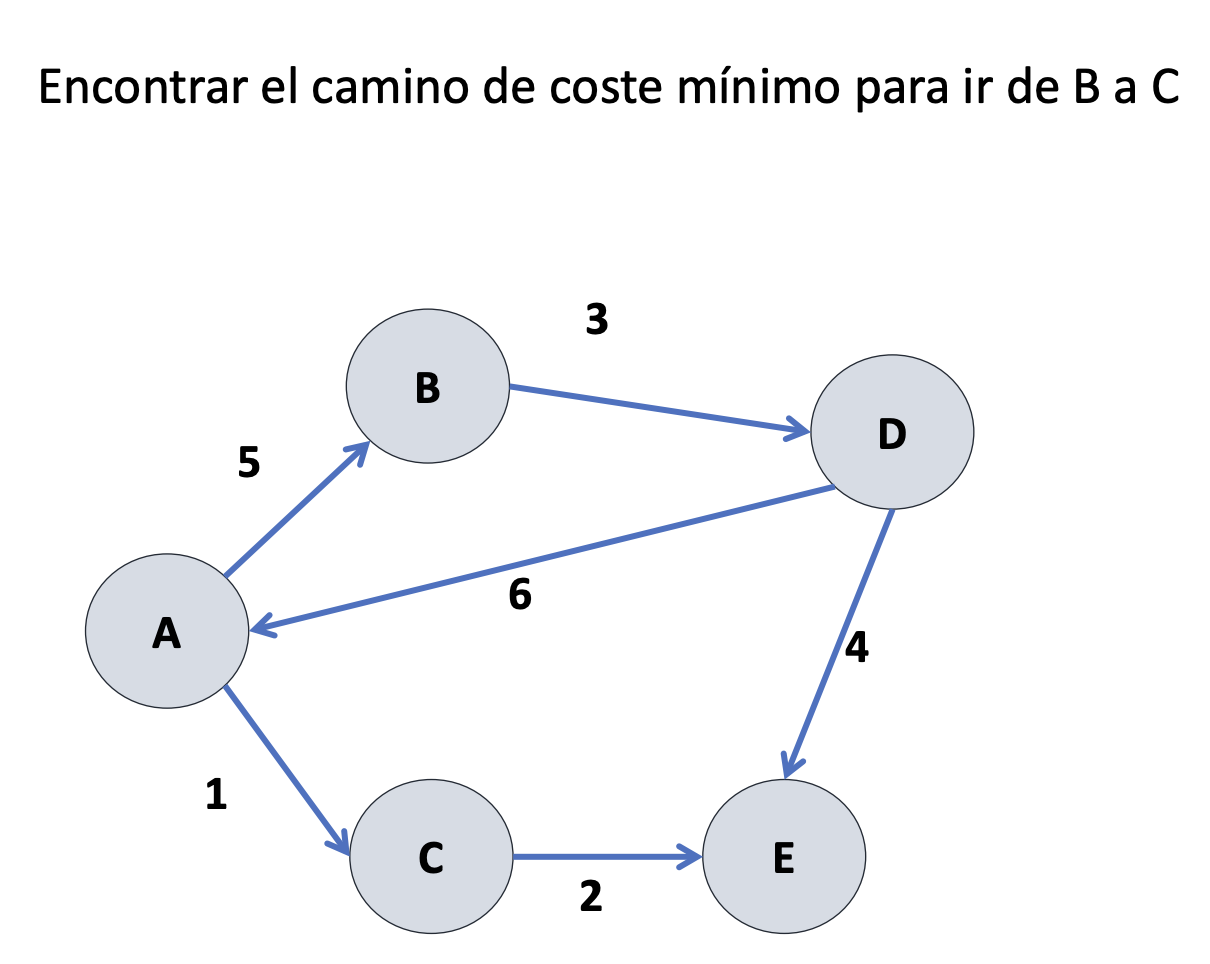
Floyd-Warshall. Ejercicio 2

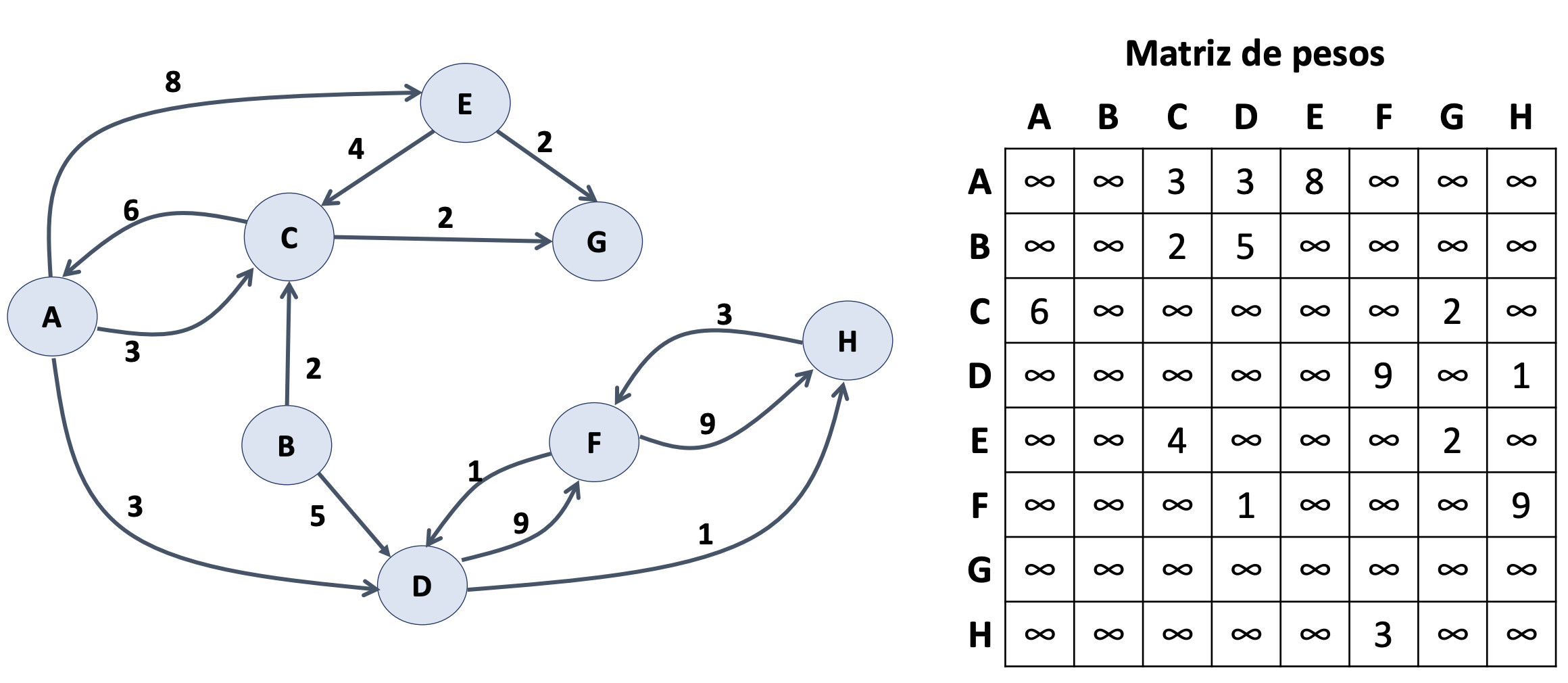
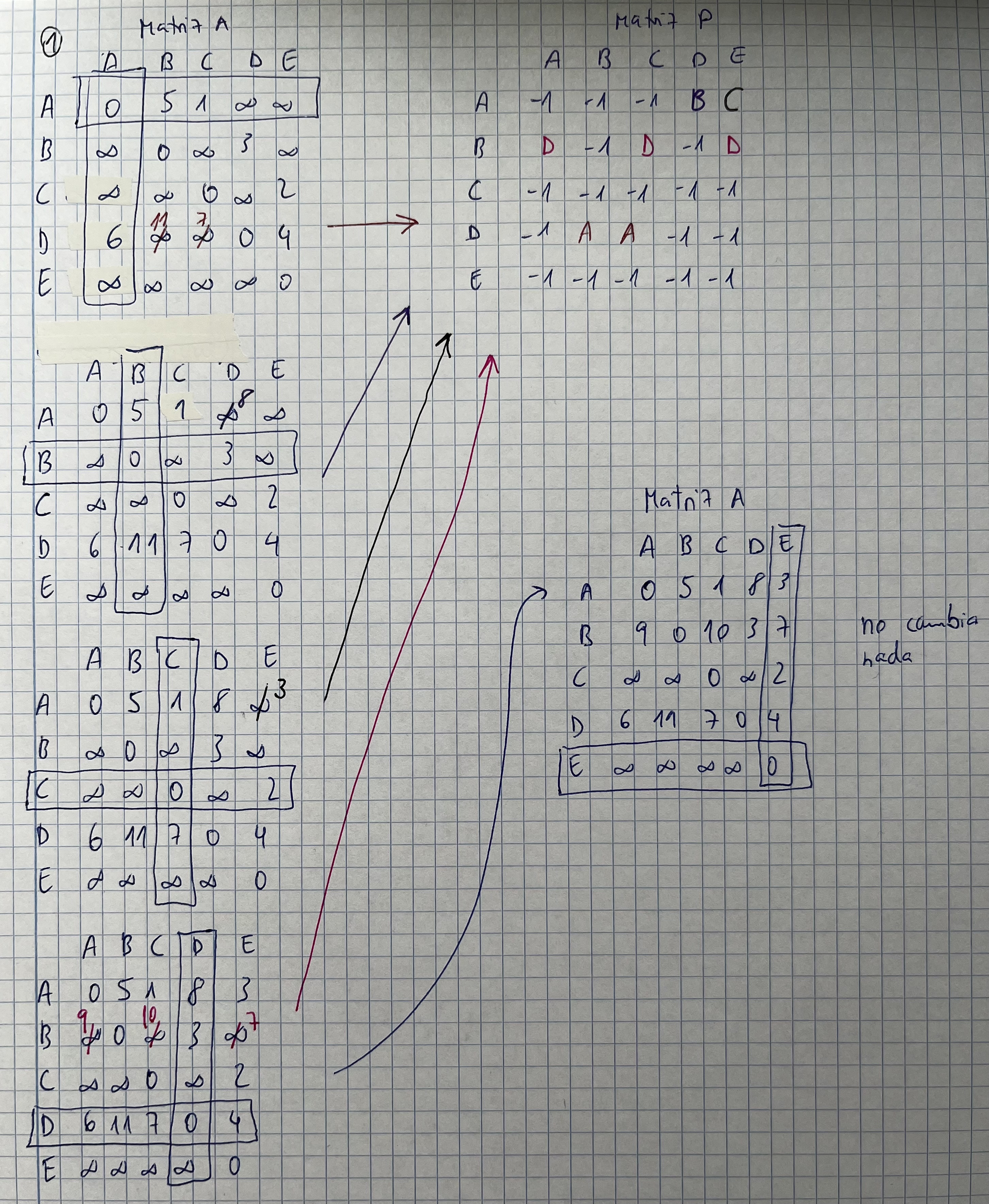
Floyd-Warshall. Ejercicio 3

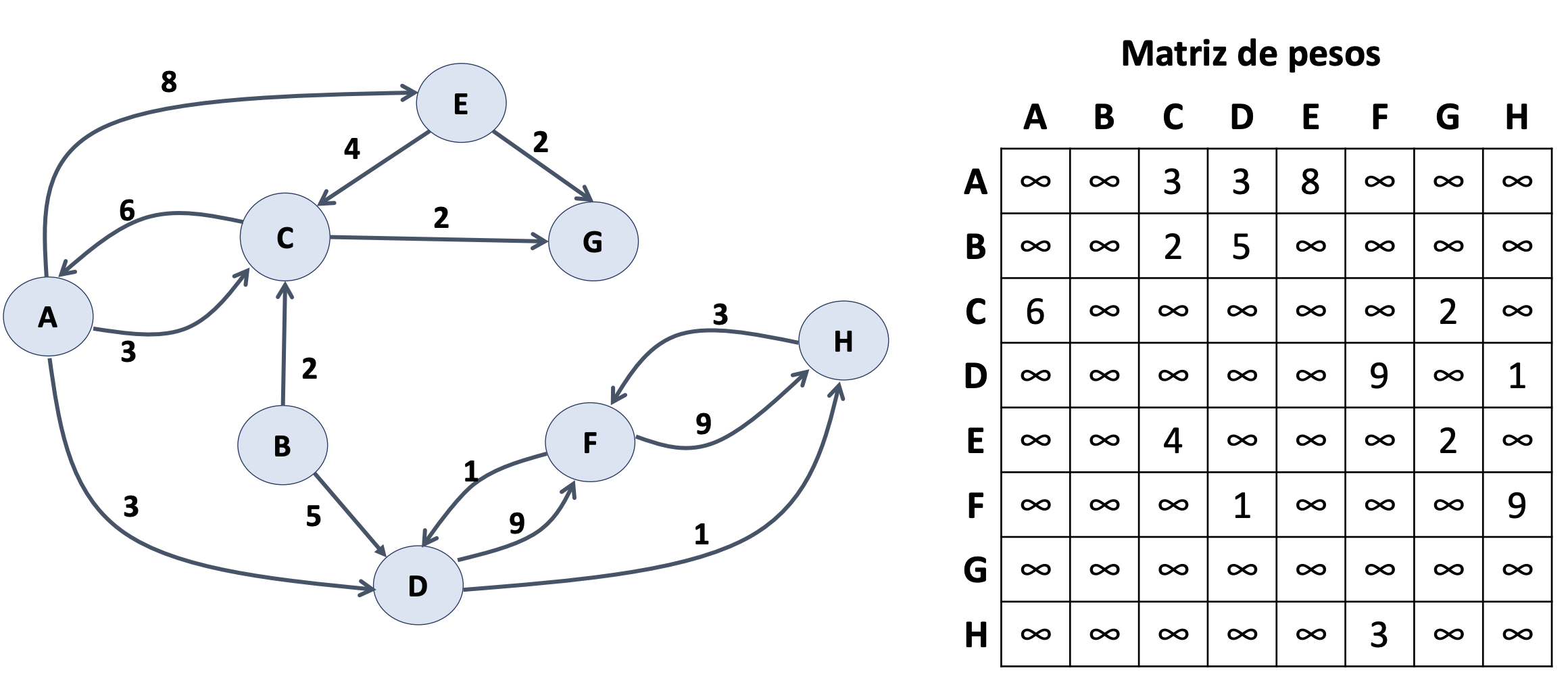
Floyd-Warshall. Ejercicio 4

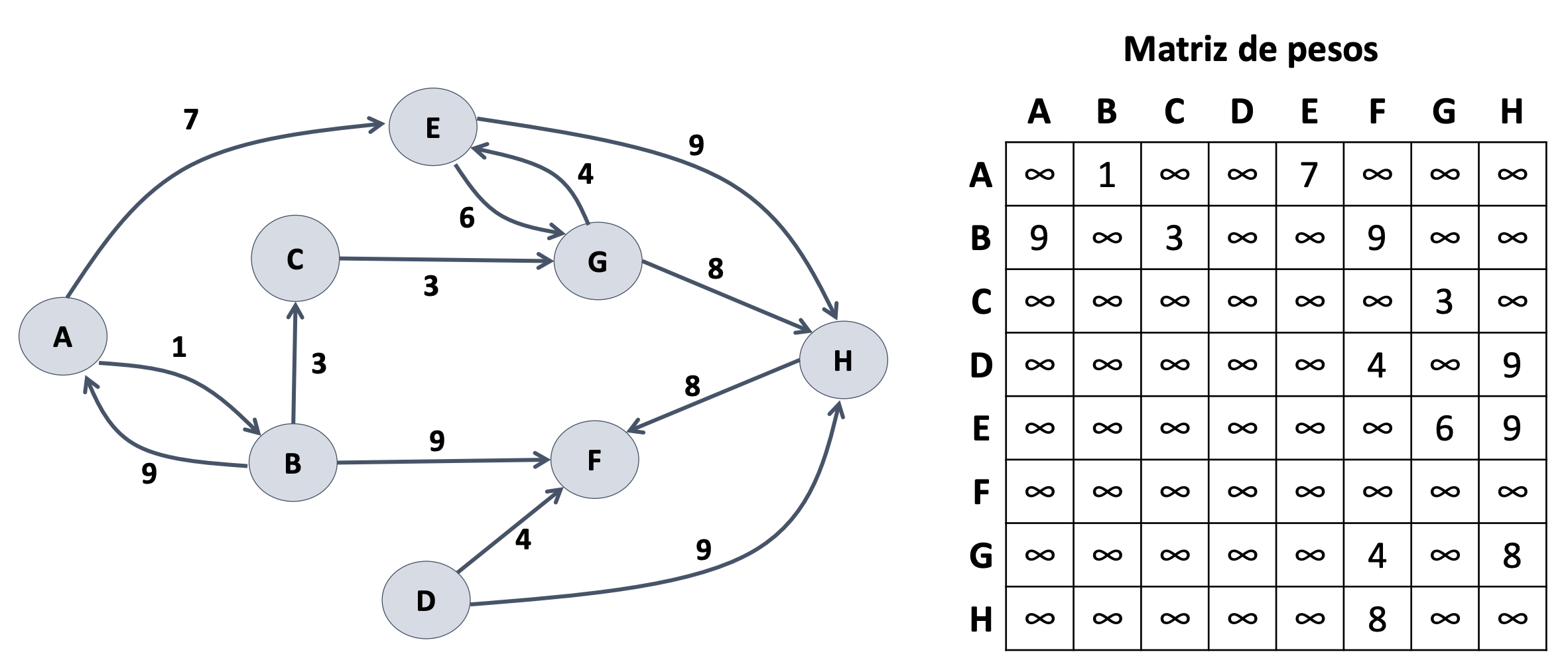
Prim. Ejercicio 5

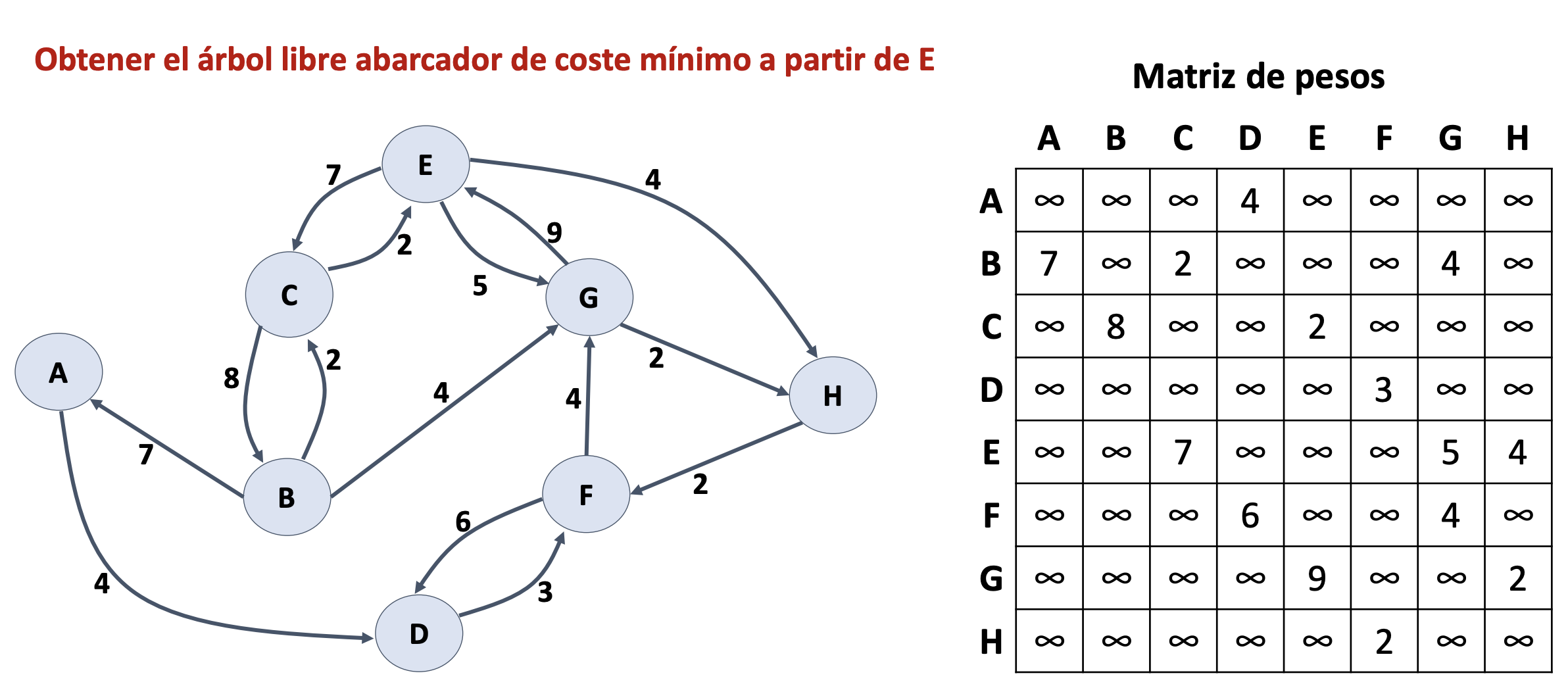
Seminario 4

BST. Ejercicio 1

Insertar 50, 25, 75, 18, 28, 100, 32, 80, 30, 40, 29, 31, 90, 95

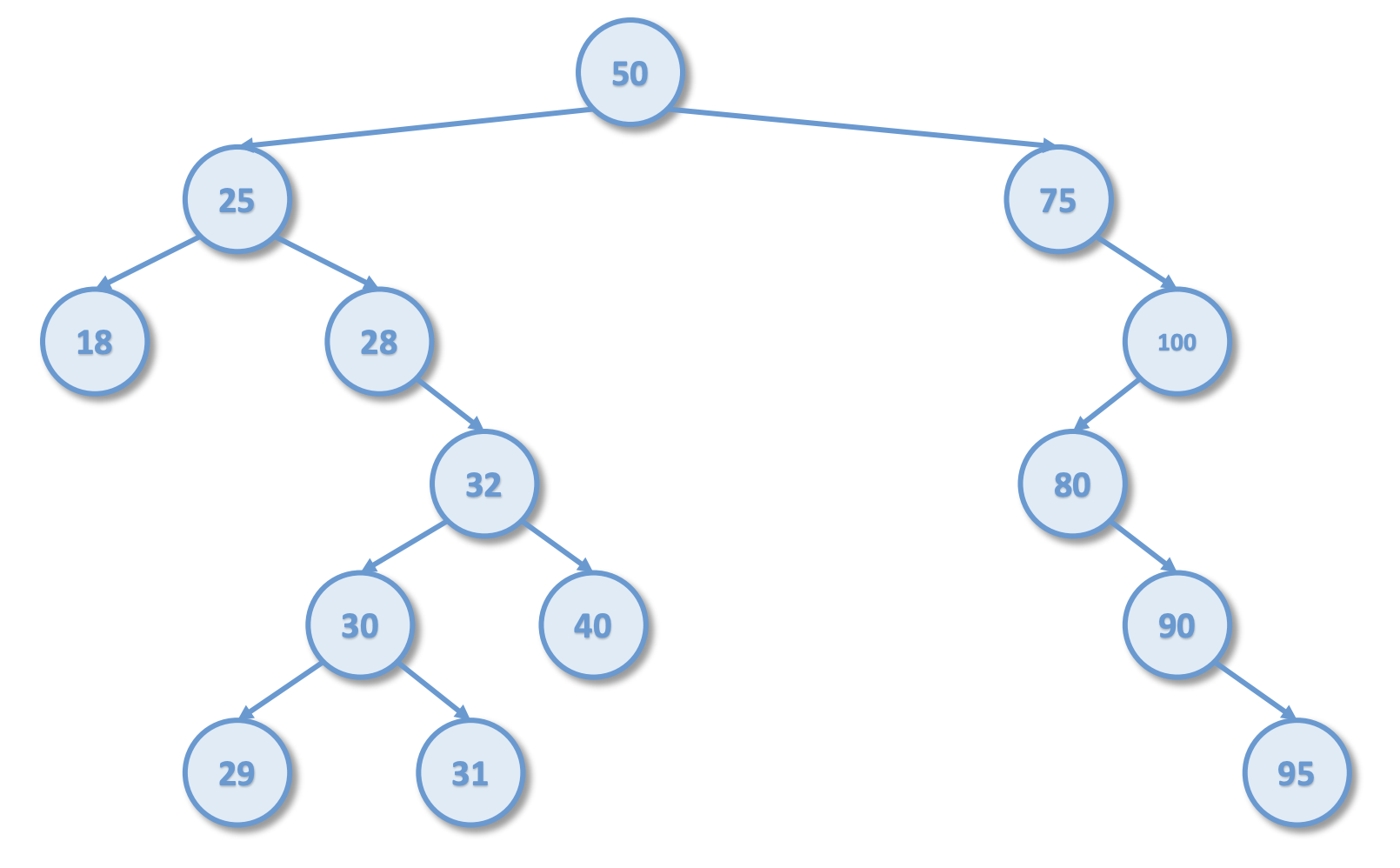
BST. Ejercicio 2

Recorrido inOrden del BST anterior

NOTA: el recorrido inOrden consiste: izquierda, raíz, derecha

Solución inOrder: 18-25-28-29-30-31-32-40-50-75-80-90-95-100

BST. Ejercicio 3

Recorrido preOrden del BST anterior

NOTA: el recorrido preOrden consiste: raíz, izquierda, derecha

Solución preOrder: 50-25-18-28-32-30-29-31-40-75-100-80-90-95

BST. Ejercicio 4

Recorrido postOrden del BST anterior

NOTA: el recorrido postOrden consiste: izquierda, derecha, raíz

Solución postOrder: 18-29-31-30-40-32-28-25-95-90-80-100-75-50

BST. Ejercicio 5

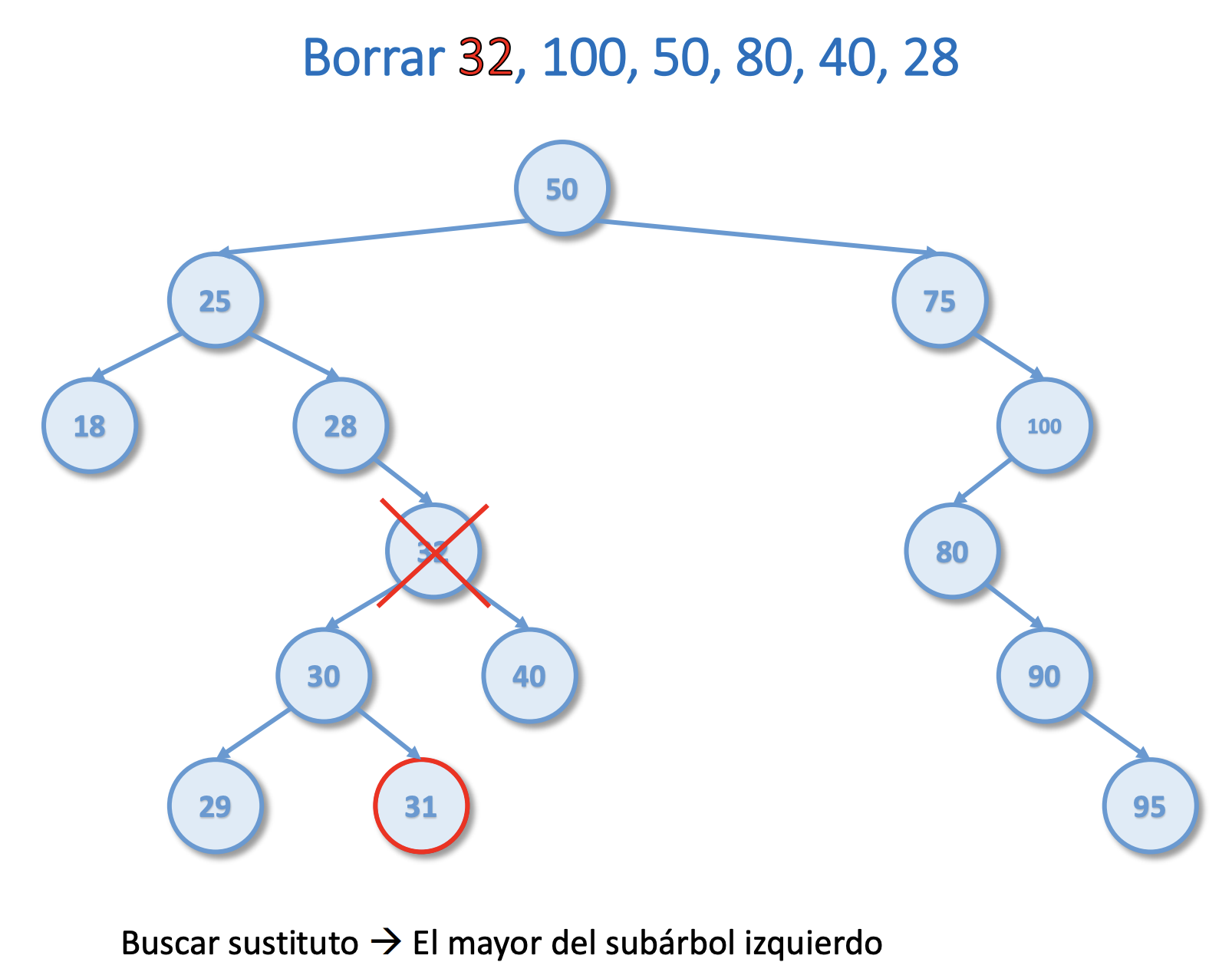
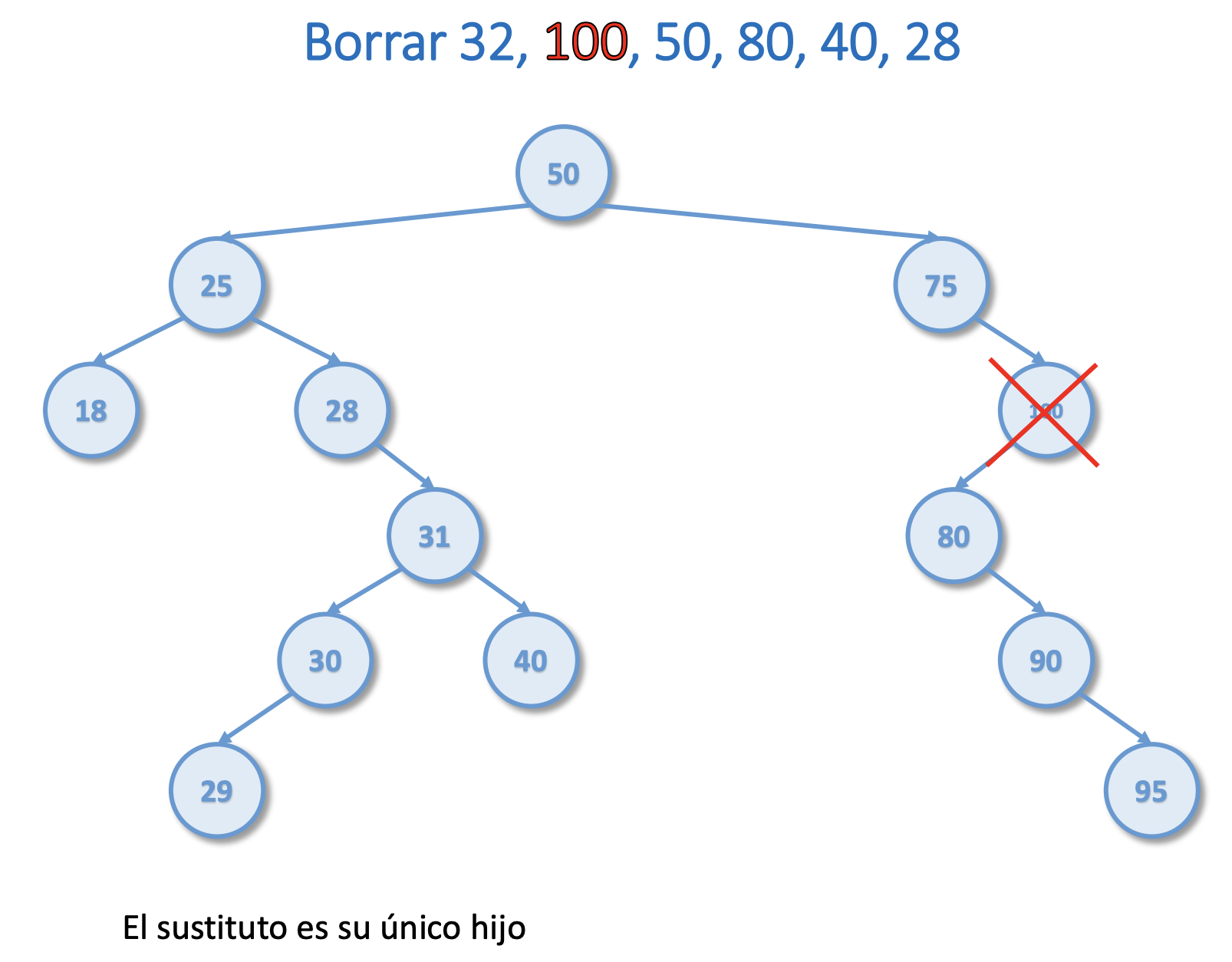
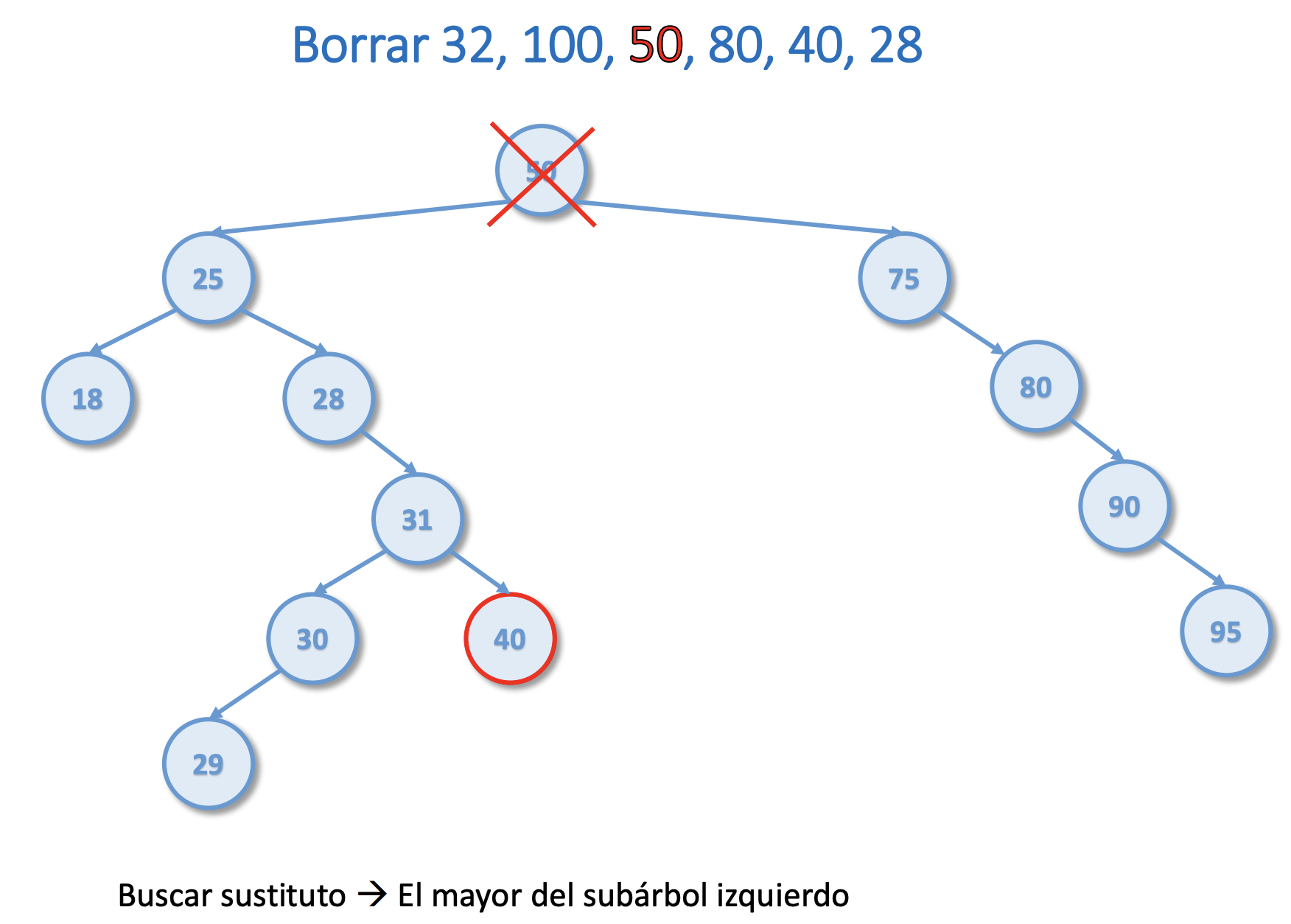
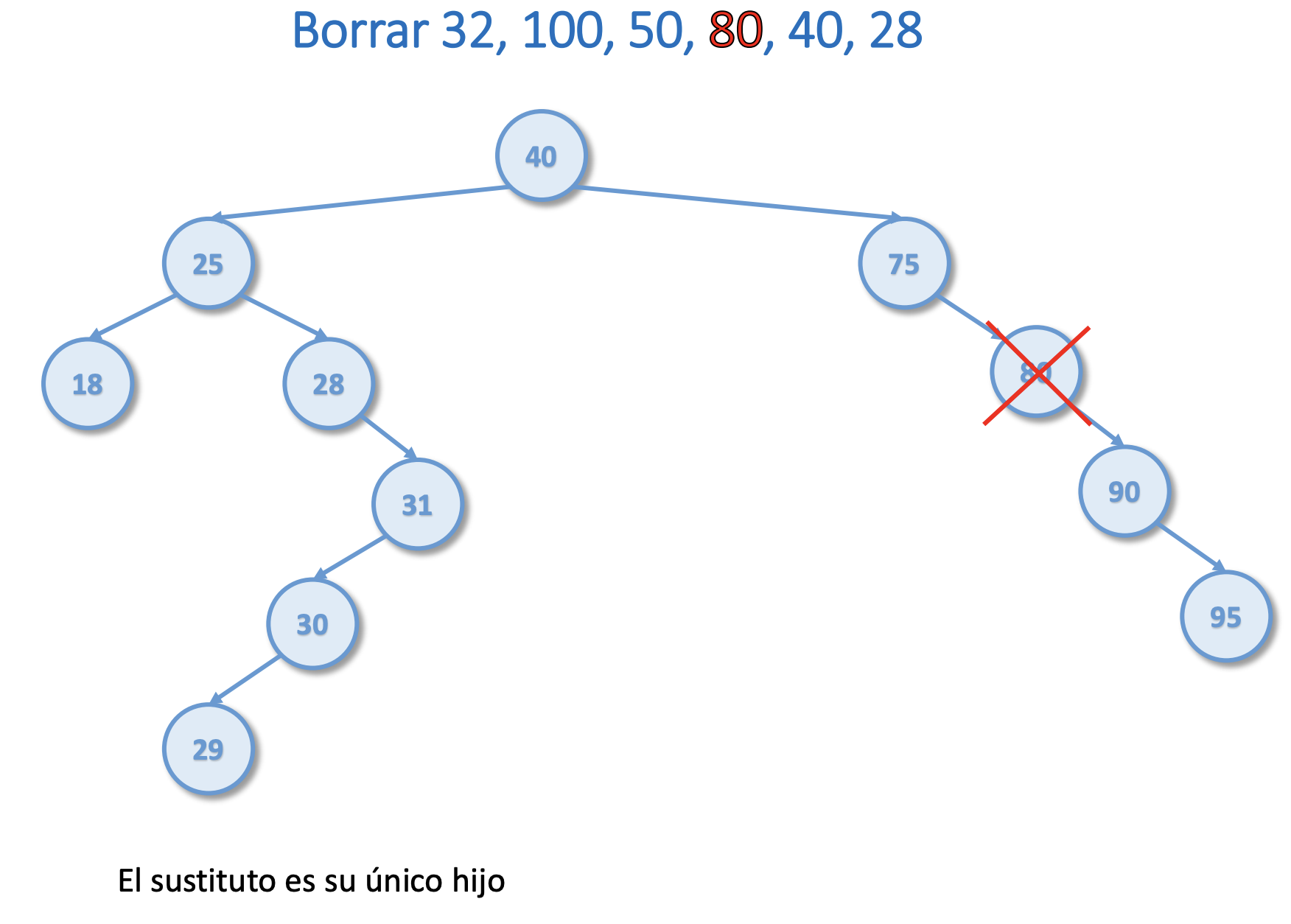
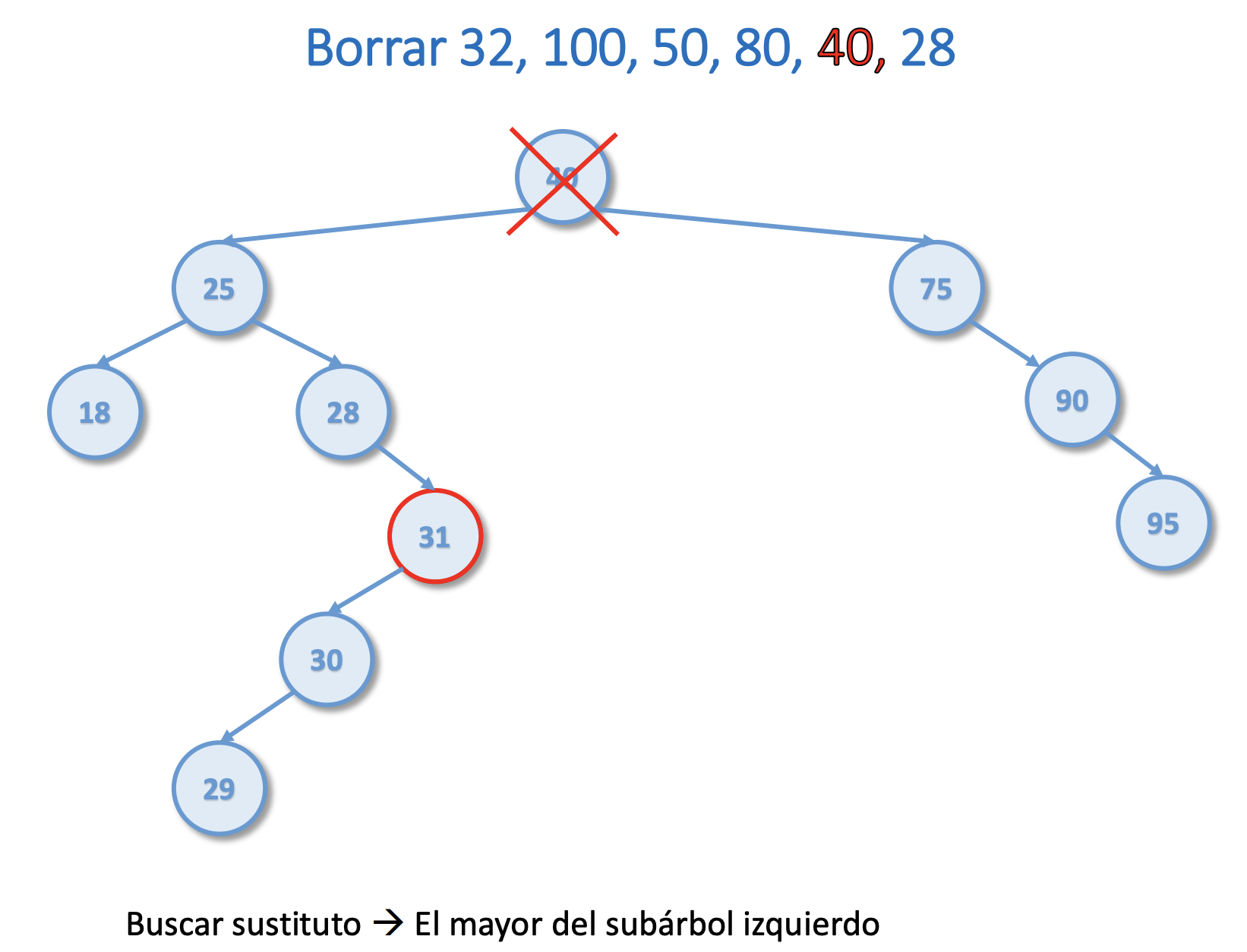
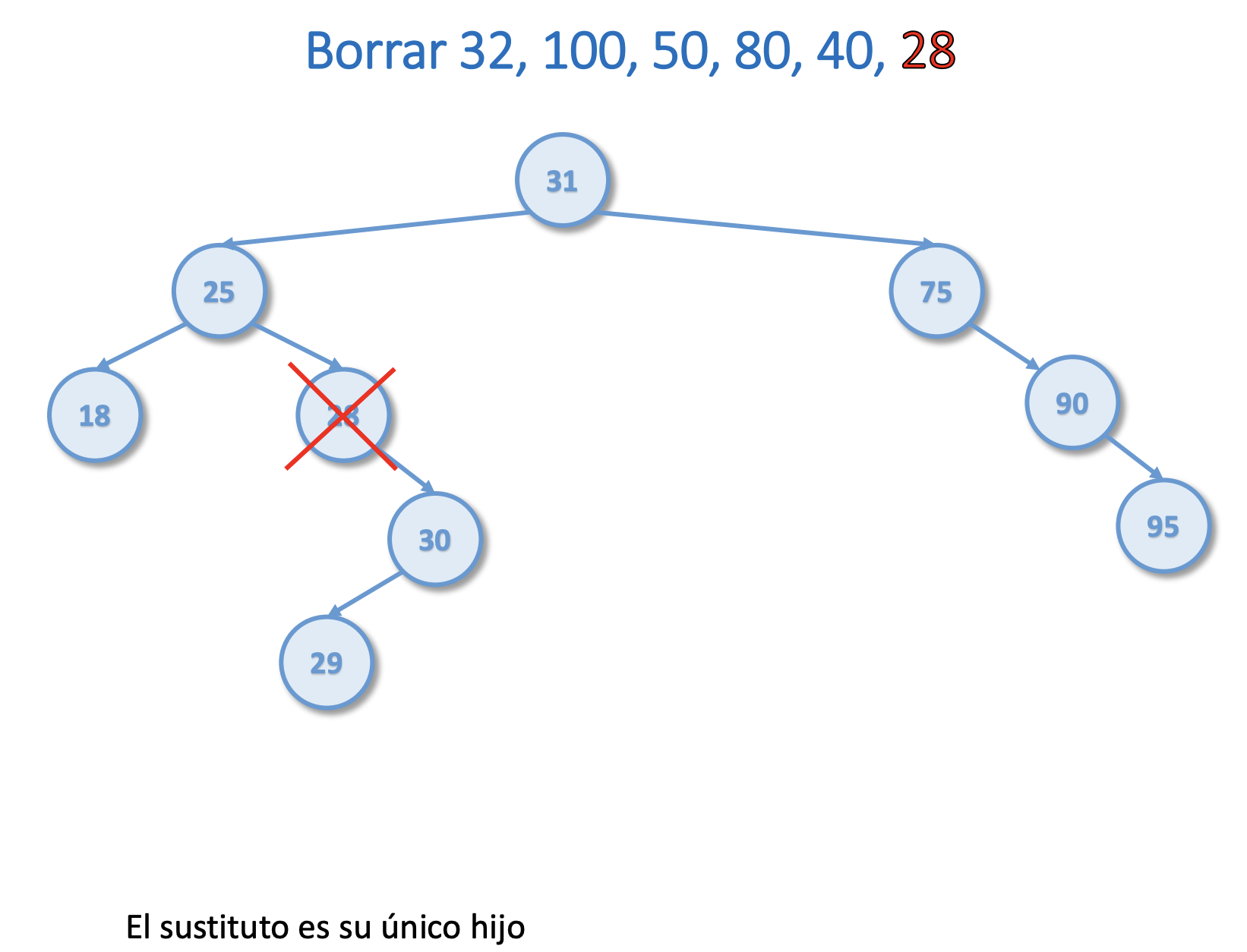
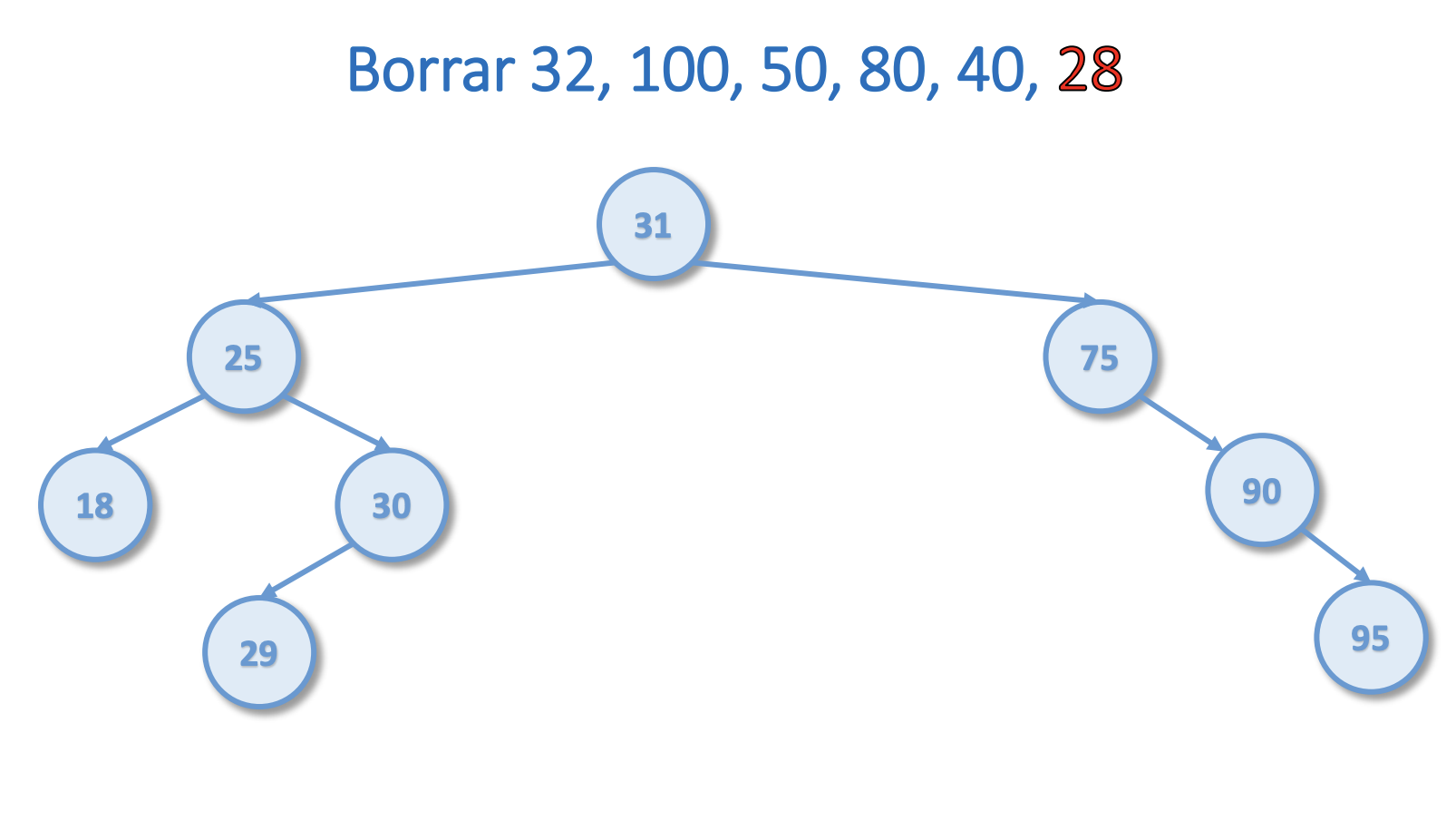
Borrar del árbol del ejercicio 1 el 32, 100, 50, 80, 40, 28

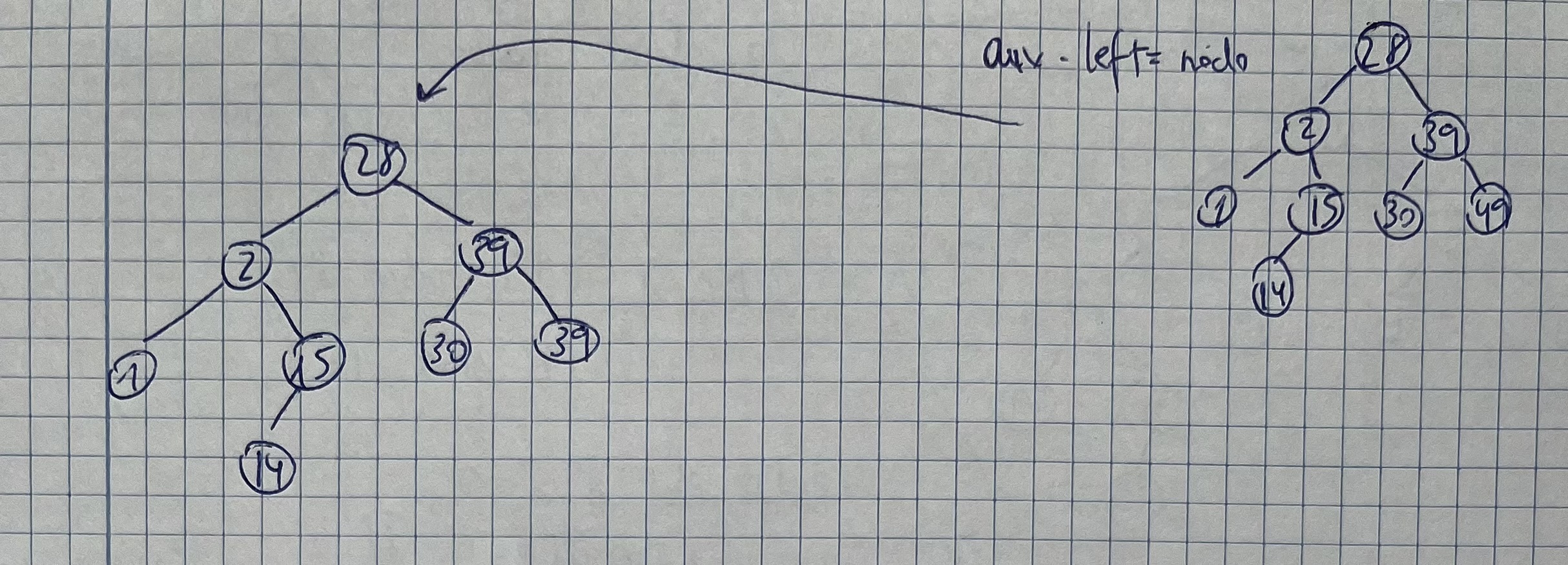
AVL. Ejercicio 1

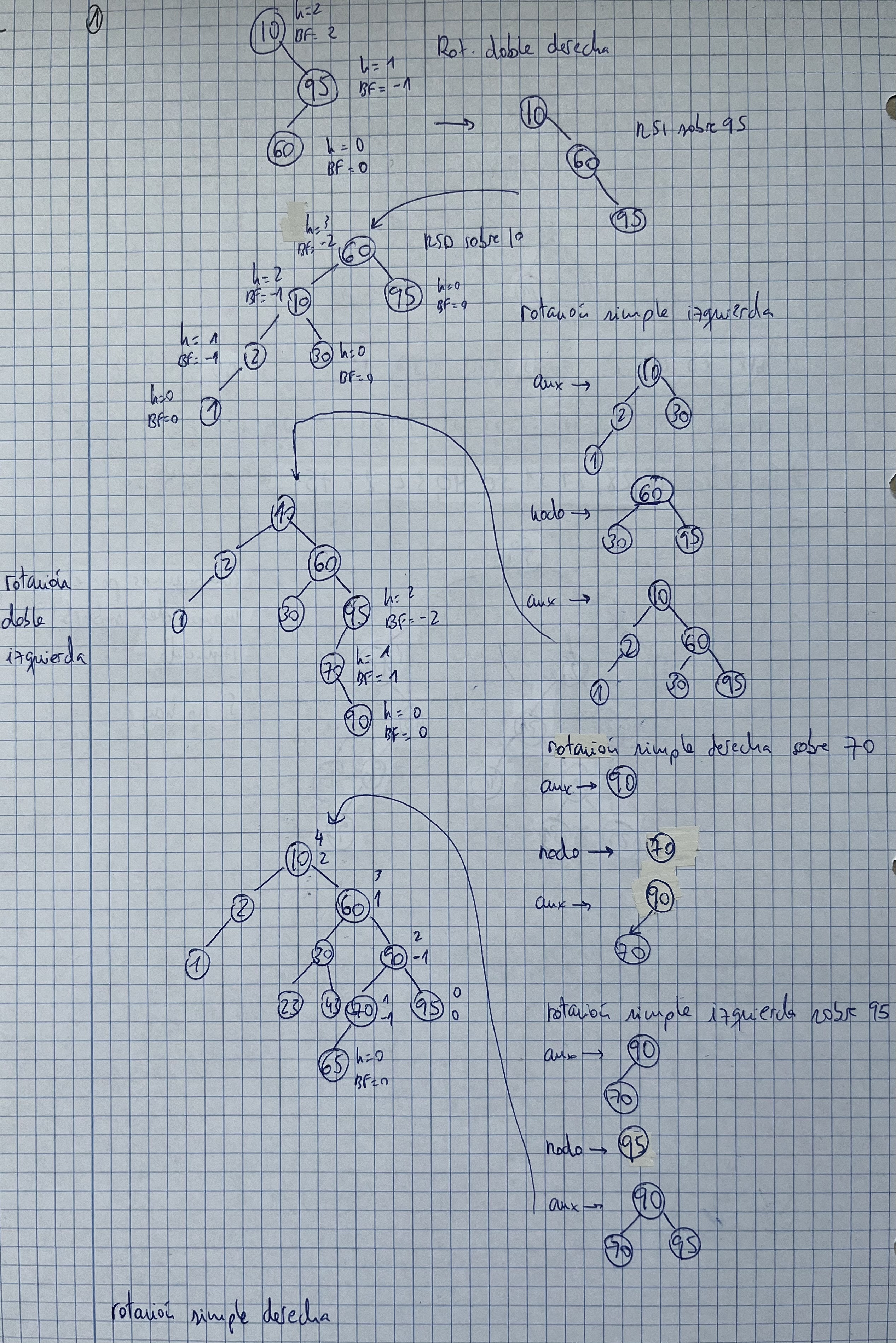
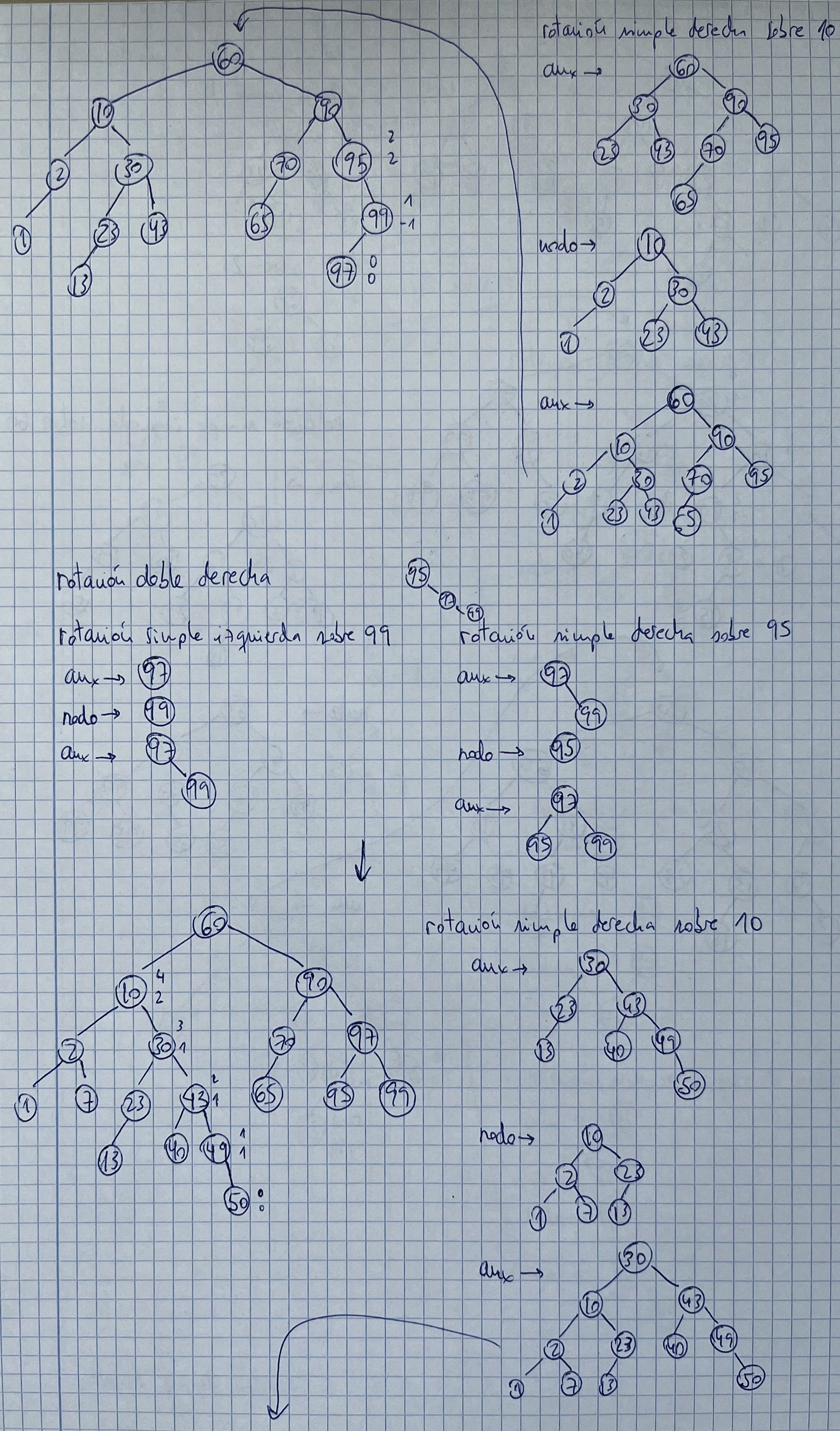
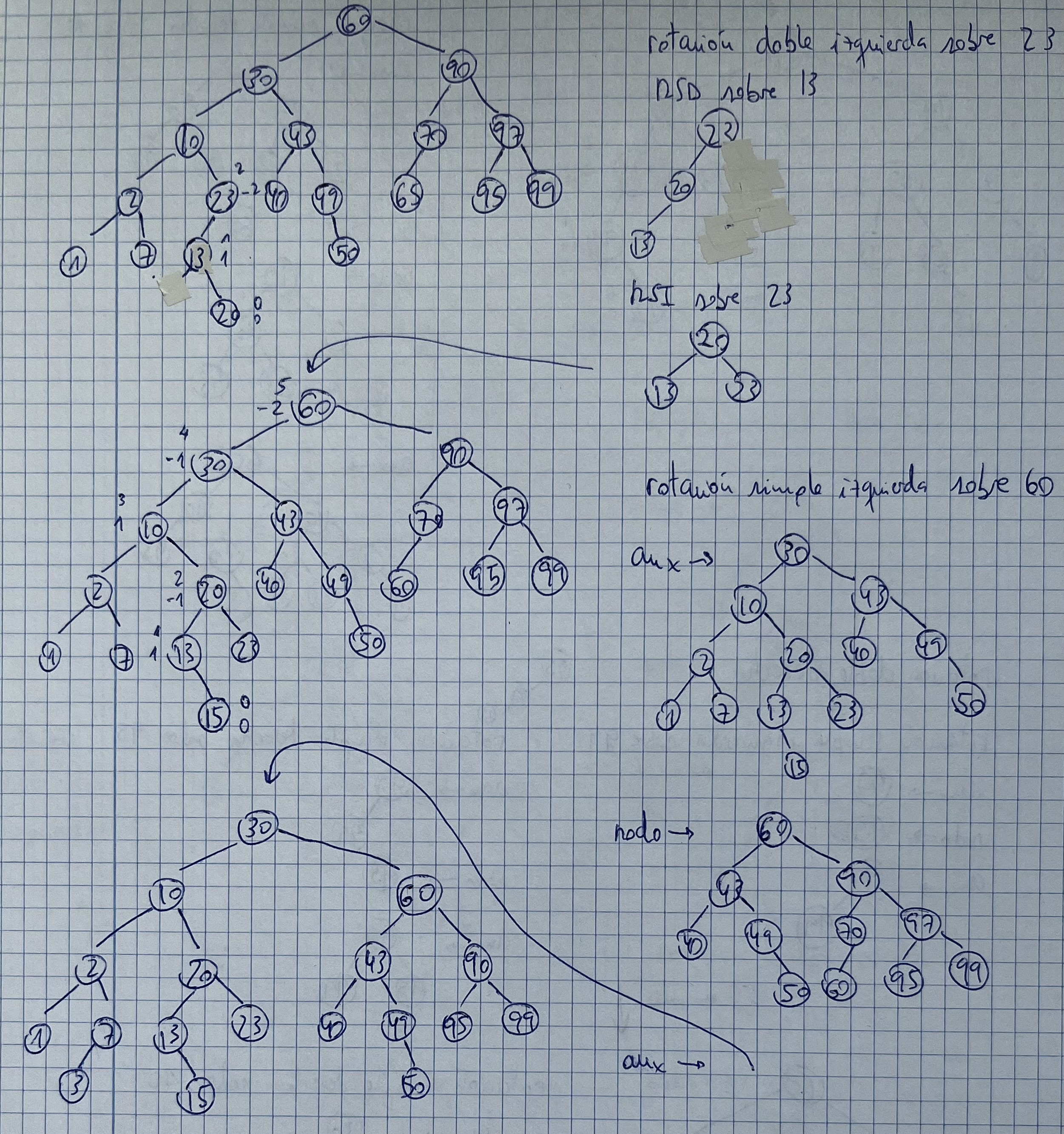
Insertar 10, 95, 60, 30, 2, 1, 70, 90, 23, 43, 65, 13, 99, 97, 49, 7, 40, 50, 20, 15, 3

Notas:

• Rotación doble derecha: bf: 2, -1
  • Hacer RSI sobre el getRight() del nodo con bf 2
  • Hacer RSD sobre el nodo con bf 2
• Rotación doble izquierda: bf: -2, 1
  • Hacer RSD sobre el getLeft() del nodo con bf -2
  • Hacer RSI sobre el nodo con bf -2
• Rotación simple derecha: bf: 2, 1
  • aux=nodo.right
  • nodo.right=aux.left
  • aux.left=nodo
• Rotación simple izquierda: bf: -2, -1
  • aux=nodo.left
  • nodo.left=aux.right
  • aux.right=nodo

Seminario 5

Árboles B

• Los nodos se llaman páginas
• Cada página puede contener 2n claves y 2n+1 hijos
• La raíz puede tener como mínimo una clave y como máximo 2n claves
• Cualquier página que no sea la raíz puede tener como mínimo n claves y como máximo 2n claves
• Insertar: mayores a la derecha del padre y menores a la izquierda
• Borrar: se busca el menor del subárbol derecho
• El árbol sólo puede crecer hacia arriba siempre y cuando el nivel tenga ya el máximo número de hijos posibles

Árboles B. Ejercicio 1

Partiendo de un árbol B de orden 2 vacío, inserta las siguientes claves en el orden que aparecen: 190, 57, 89, 90, 121, 170, 35, 48, 91, 22, 126, 132, 80

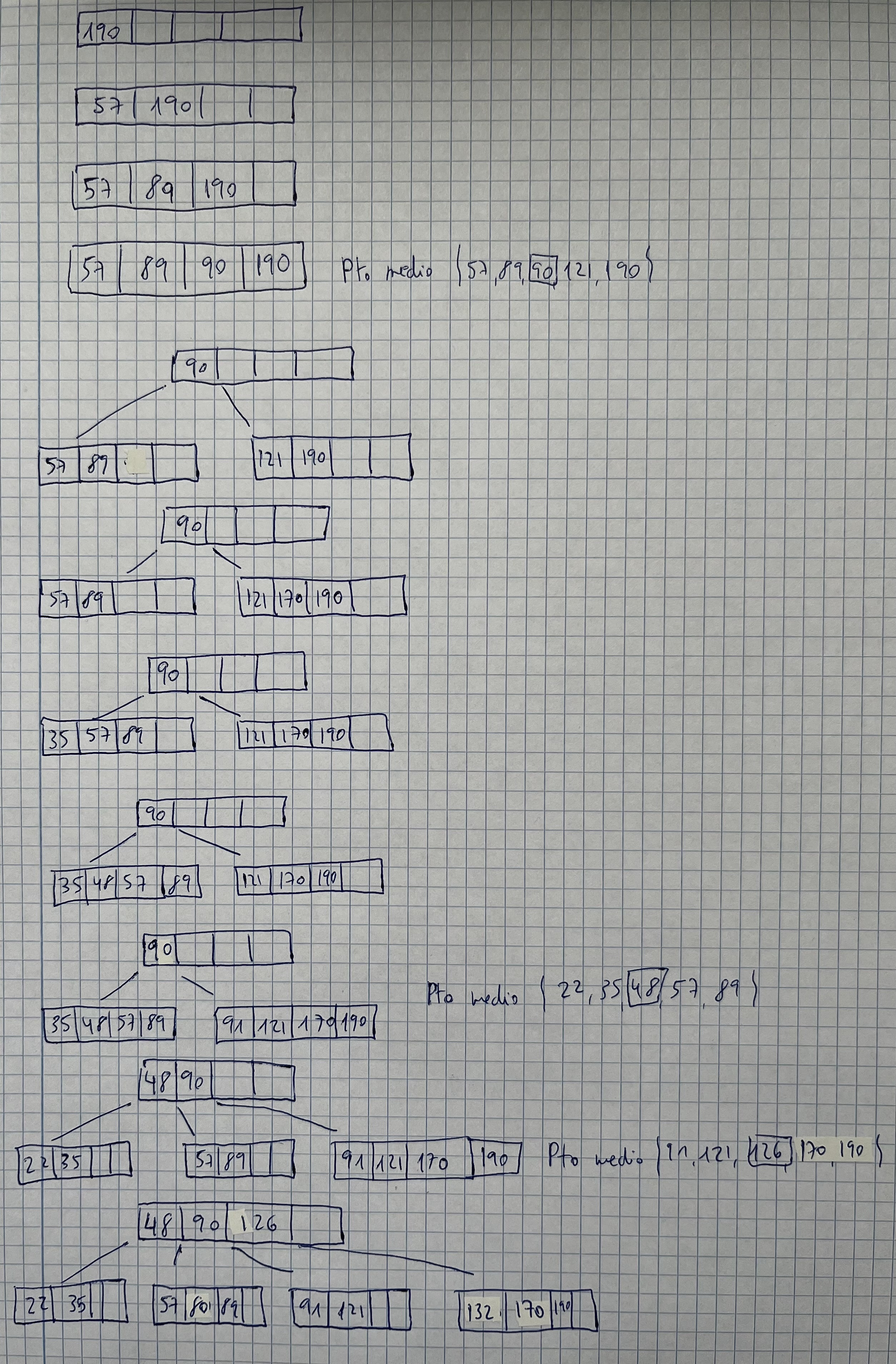
Árboles B. Ejercicio 2

Partiendo de un árbol B de orden 2 anterior, borrar las siguientes claves en el orden que aparecen: 80, 91, 57, 170, 48, 126, 22, 90, 89

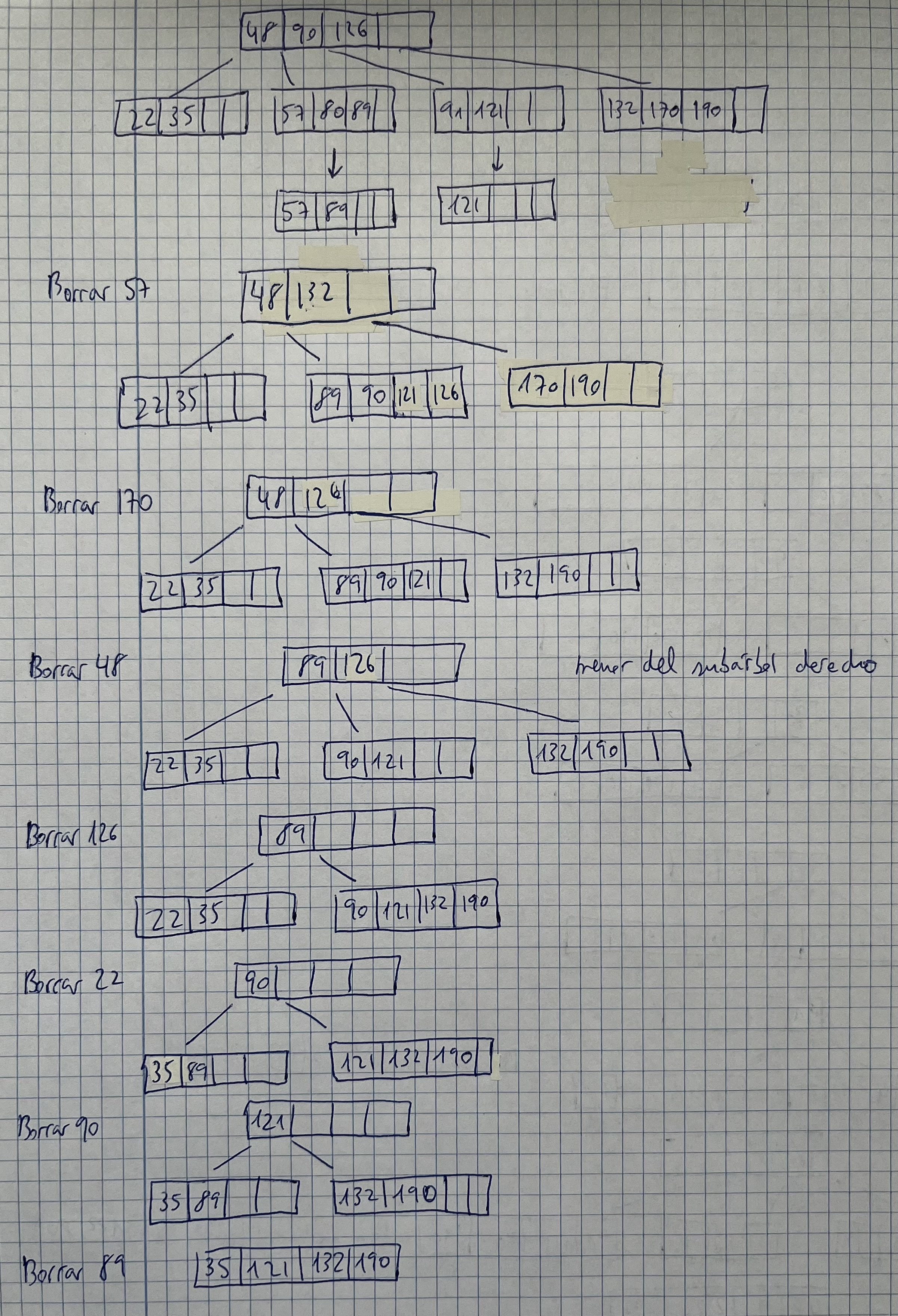
Árboles B. Ejercicio 3

Partiendo de un árbol B de orden 2 insertar las siguientes claves en el orden que aparecen: 60, 40, 80, 20, 55, 65, 63, 51, 75, 2, 4, 90, 95, 100, 41, 42, 50, 22, 30, 25, 31, 32, 33, 36, 38, 39

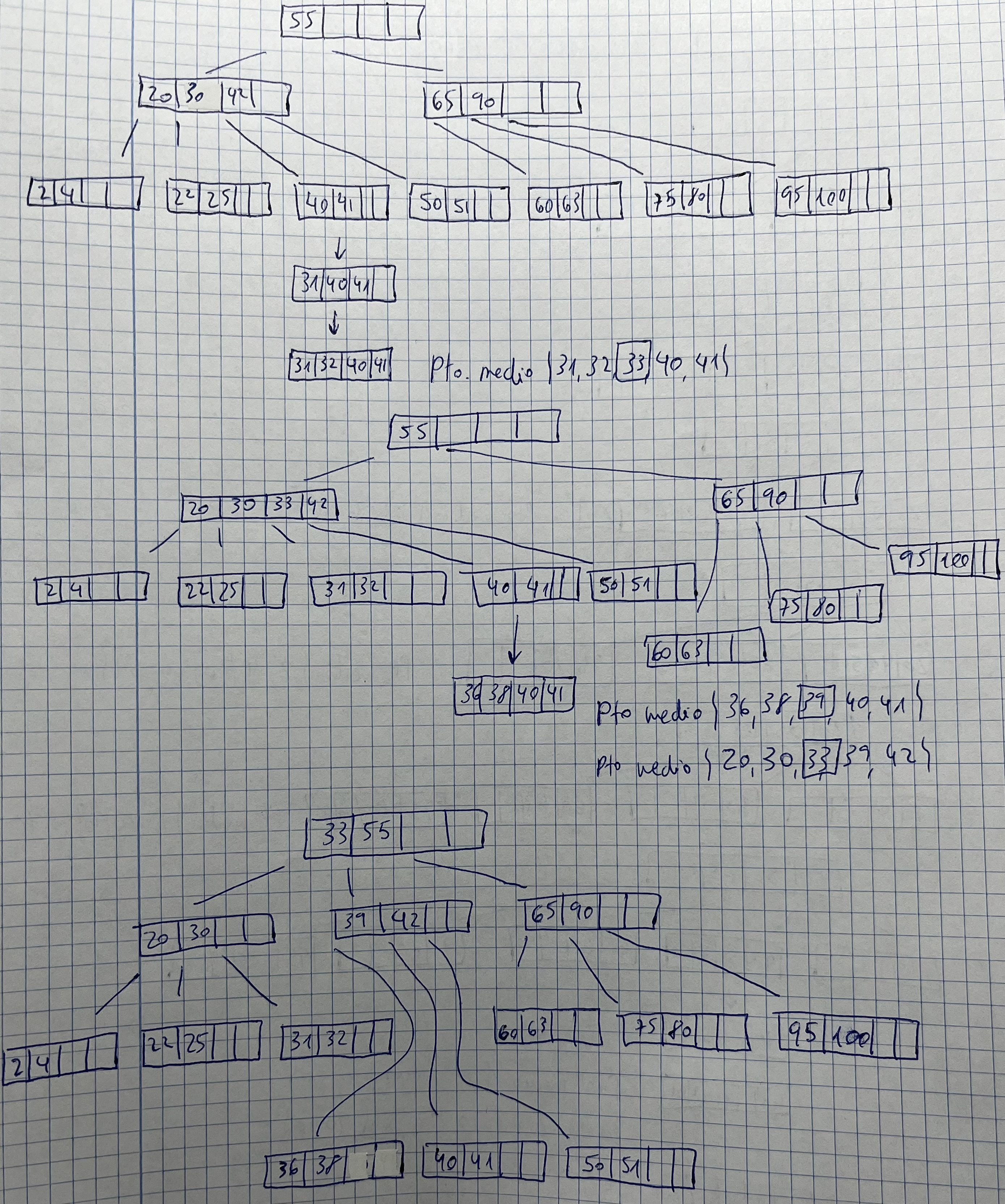
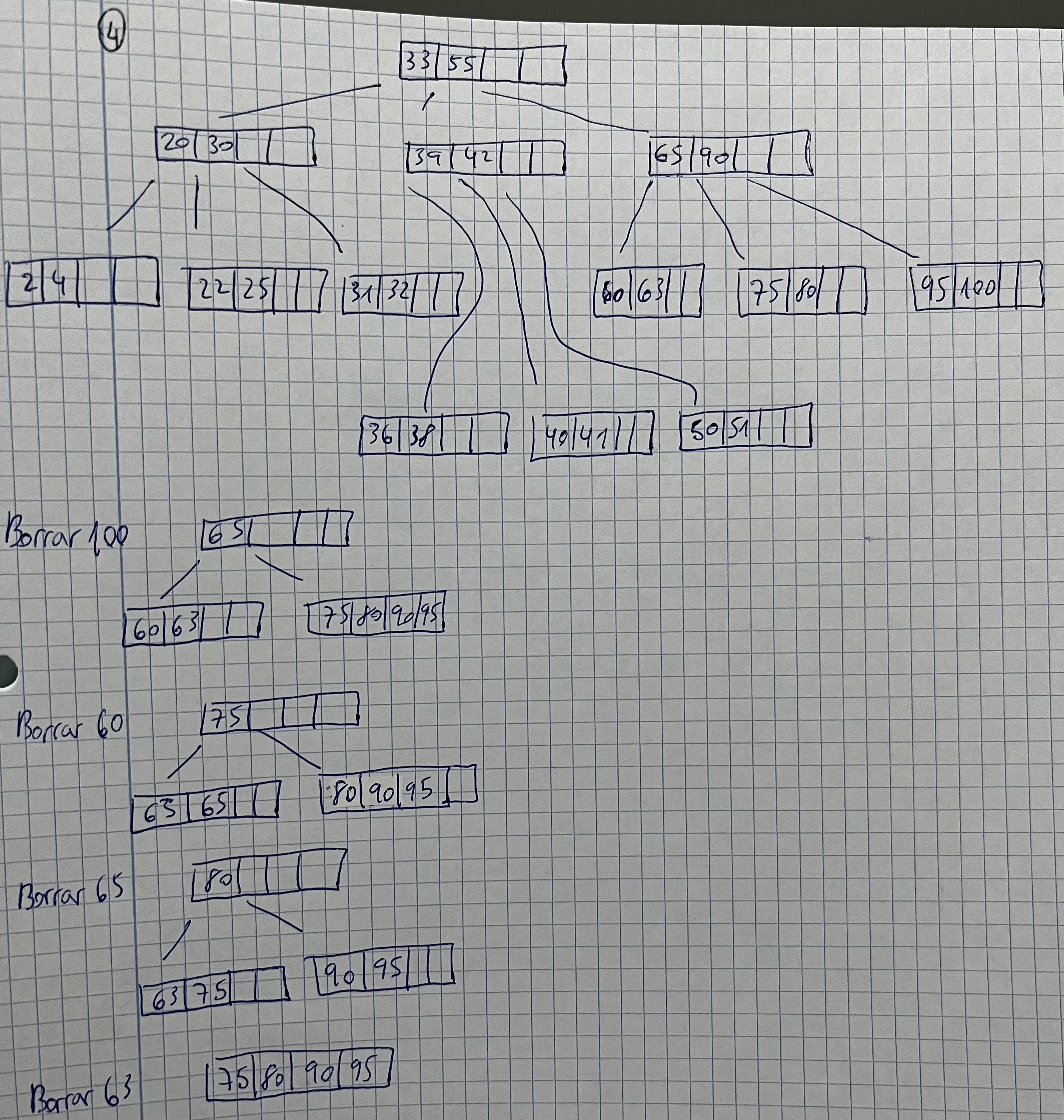
Árboles B. Ejercicio 4

Partiendo del árbol B de orden 2 anterior, borrar las siguientes claves en el orden que aparecen: 100, 60, 65, 63

Montículo binario de mínimos

• Vector de n elementos

• Insertar: se inserta el nuevo elemento al final y se realiza un filtrado ascendente

• Sacar: se mueve el último elemento de la raíz y se realiza un filtrado descendente

• Borrar: se mueve el último elemento a la posición del elemento a borrar y se realiza un filtrado descendente

• El padre está en la posición: (i-1)/2

• El hijo izquierdo está en la posición: (2*i)+1

• El hijo derecho está en la posición: (2*i)+2

Montículos. Ejercicio 1

Insertar las siguientes claves en un montículo binario de mínimos: 60, 40, 80, 20, 55, 65, 63, 51, 75, 2, 4, 90, 95, 99, 41, 42, 50, 22, 30, 25, 31, 32, 33, 36, 38, 39

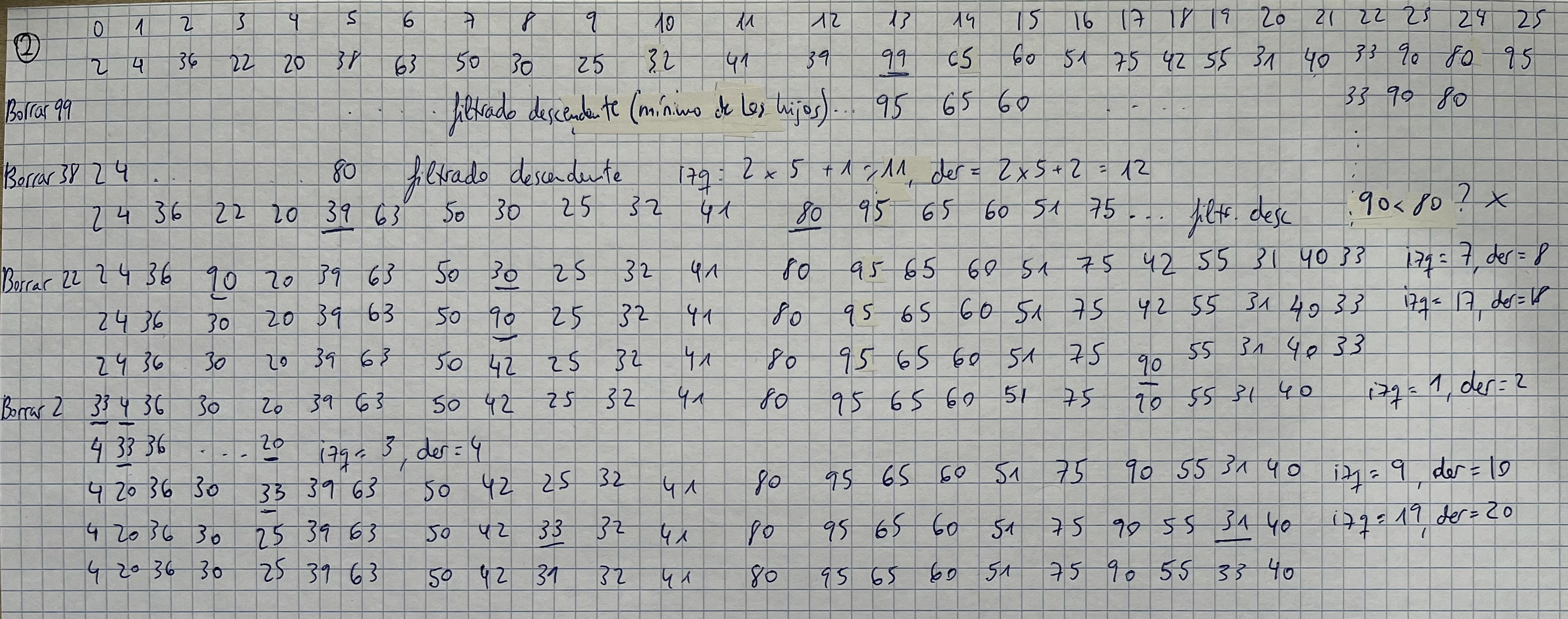
Montículos. Ejercicio 2

En el montículo generado en el ejercicio anterior borrar las siguientes claves: 99, 38, 22, 2

Seminario 6. De todo un poco

Grafos

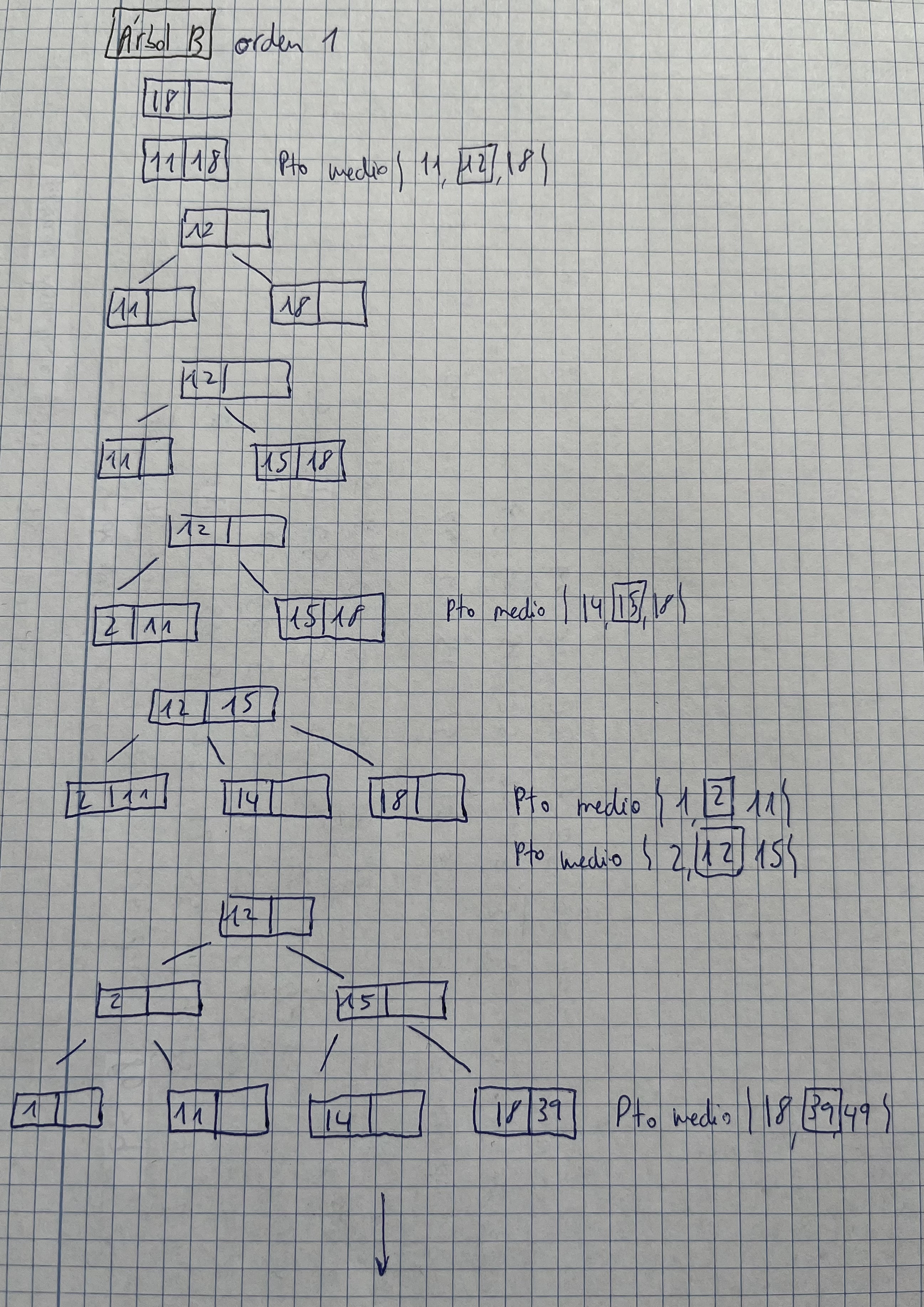
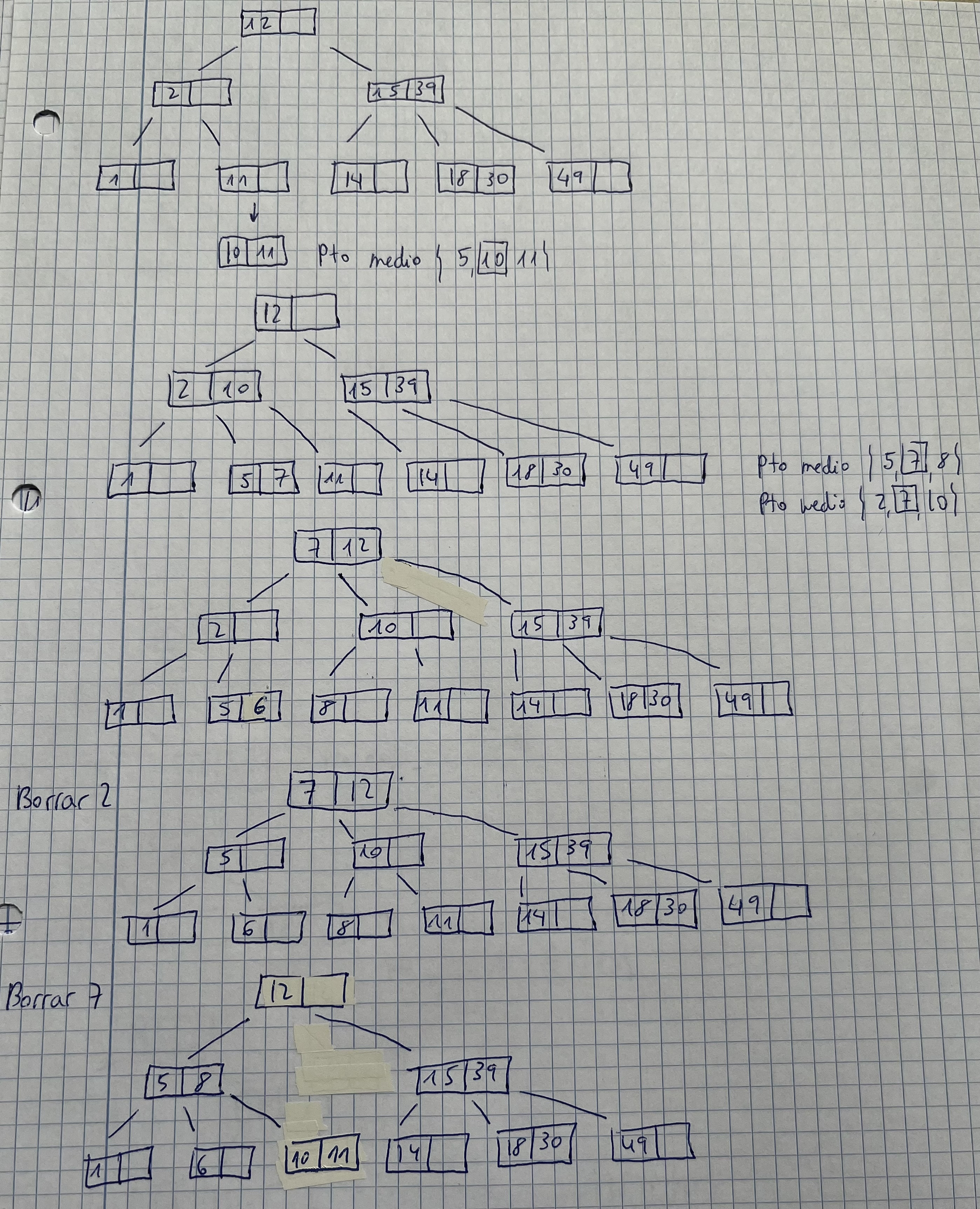
Árboles B

Árboles AVL

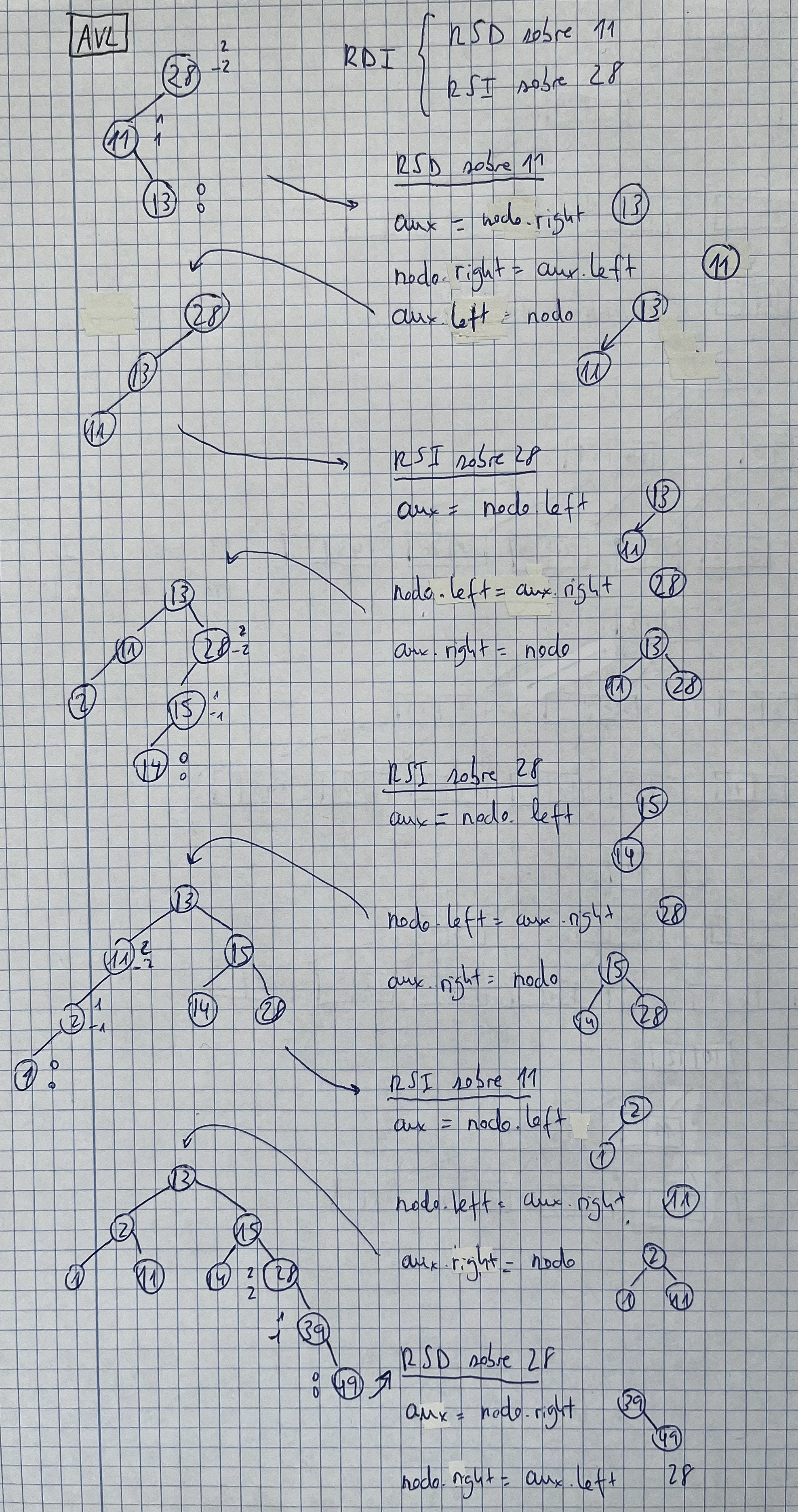
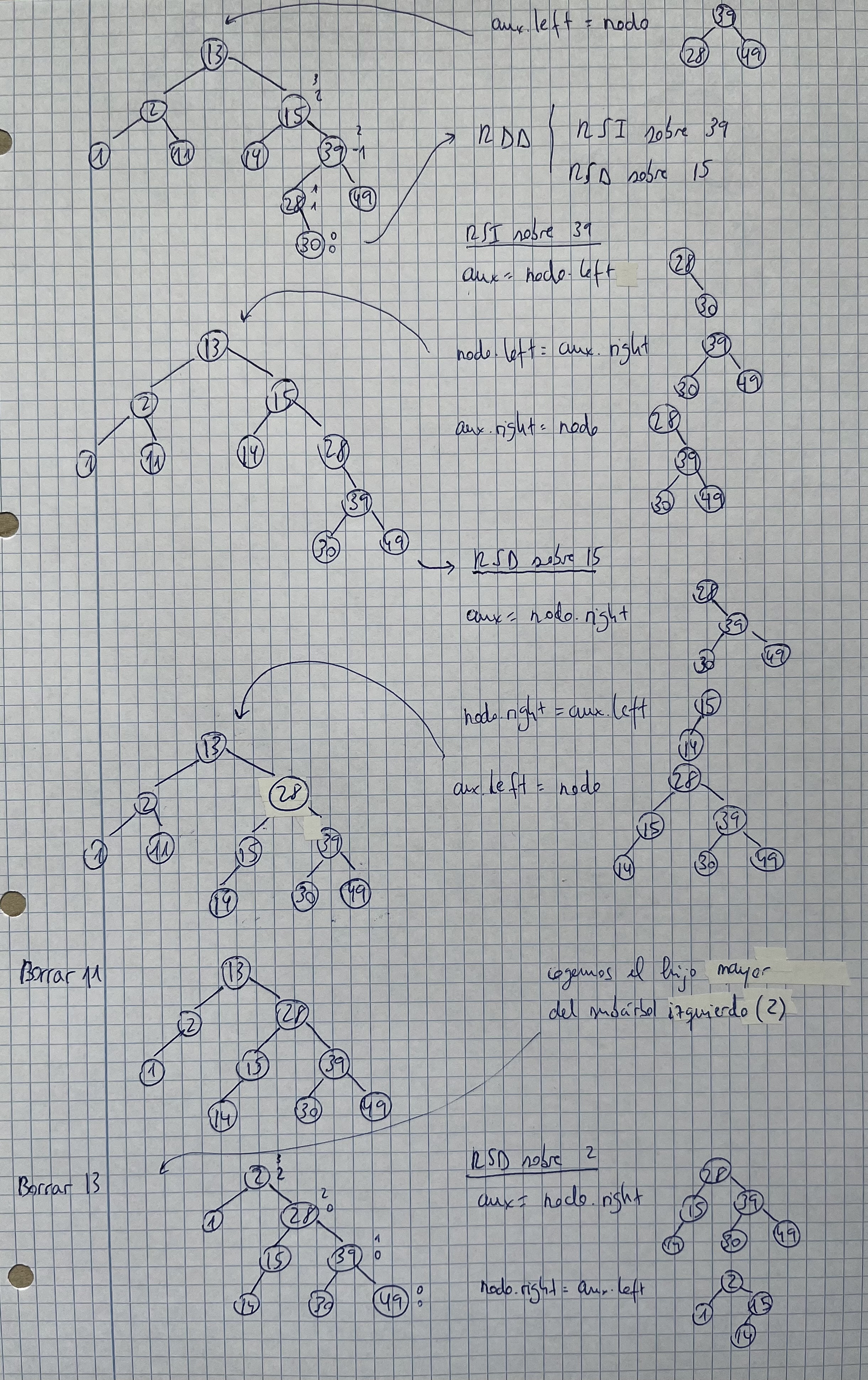
Colas de prioridad

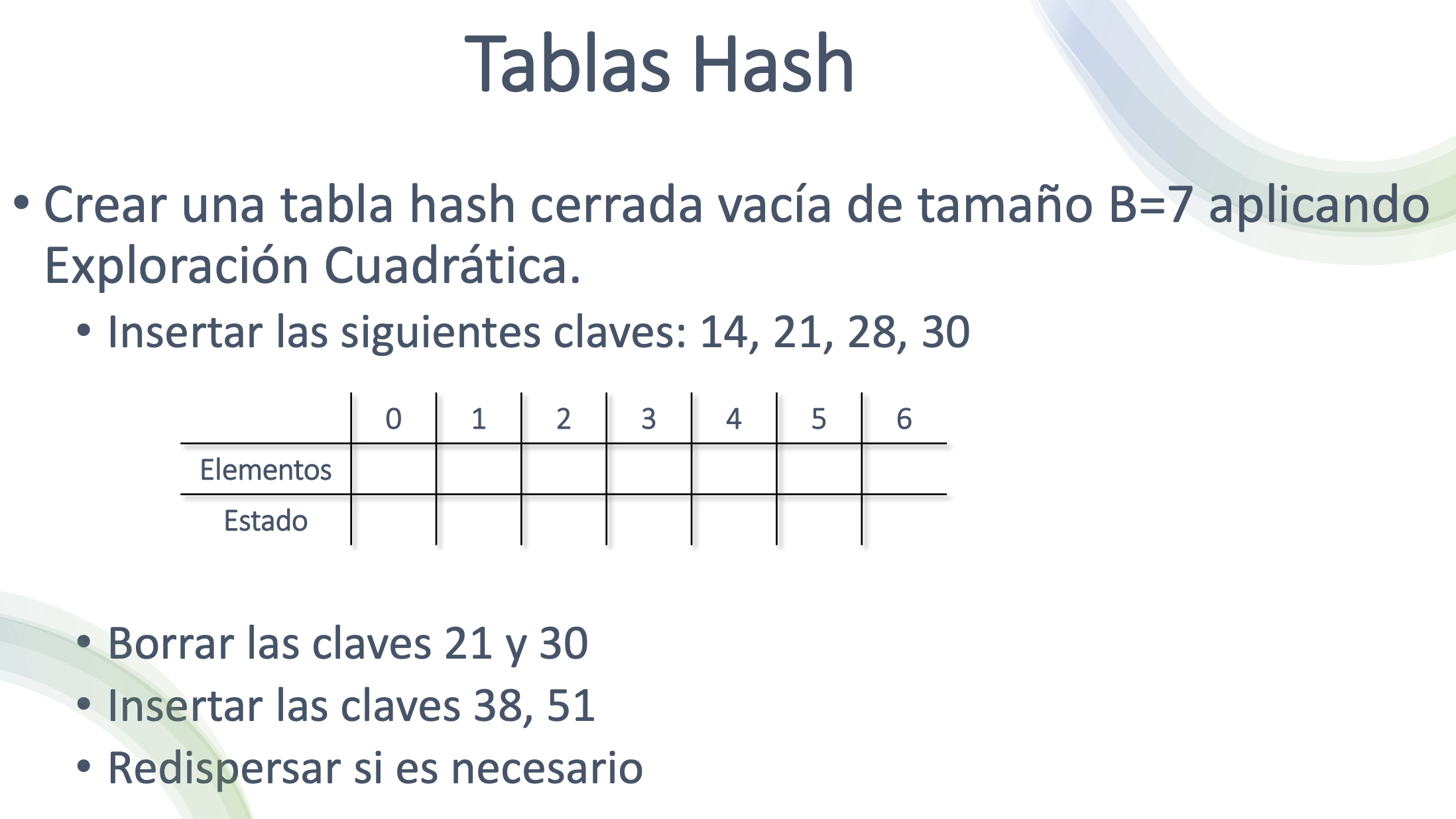
Tablas Hash

• Exploración Lineal: (h(x)+i) mod B

  • h(x) es la posición origen de la colisión
  • i es el número de intentos (0, 1, 2, 3…)
  • B es el tamaño de la tabla hash (número primo)

• Exploración Cuadrática: (h(x)+i^2) mod B

• Dispersión doble: (h(x)+i*H(x)) mod B

  • H(x) es una función de cálculo de salto. Se recomienda:
    • H(x)= R - h(x) % R
    • R es el número primo antecesor de B

• Redispersión: LF > 0.5

• Redispersión inversa: LF < 0.16