Árboles
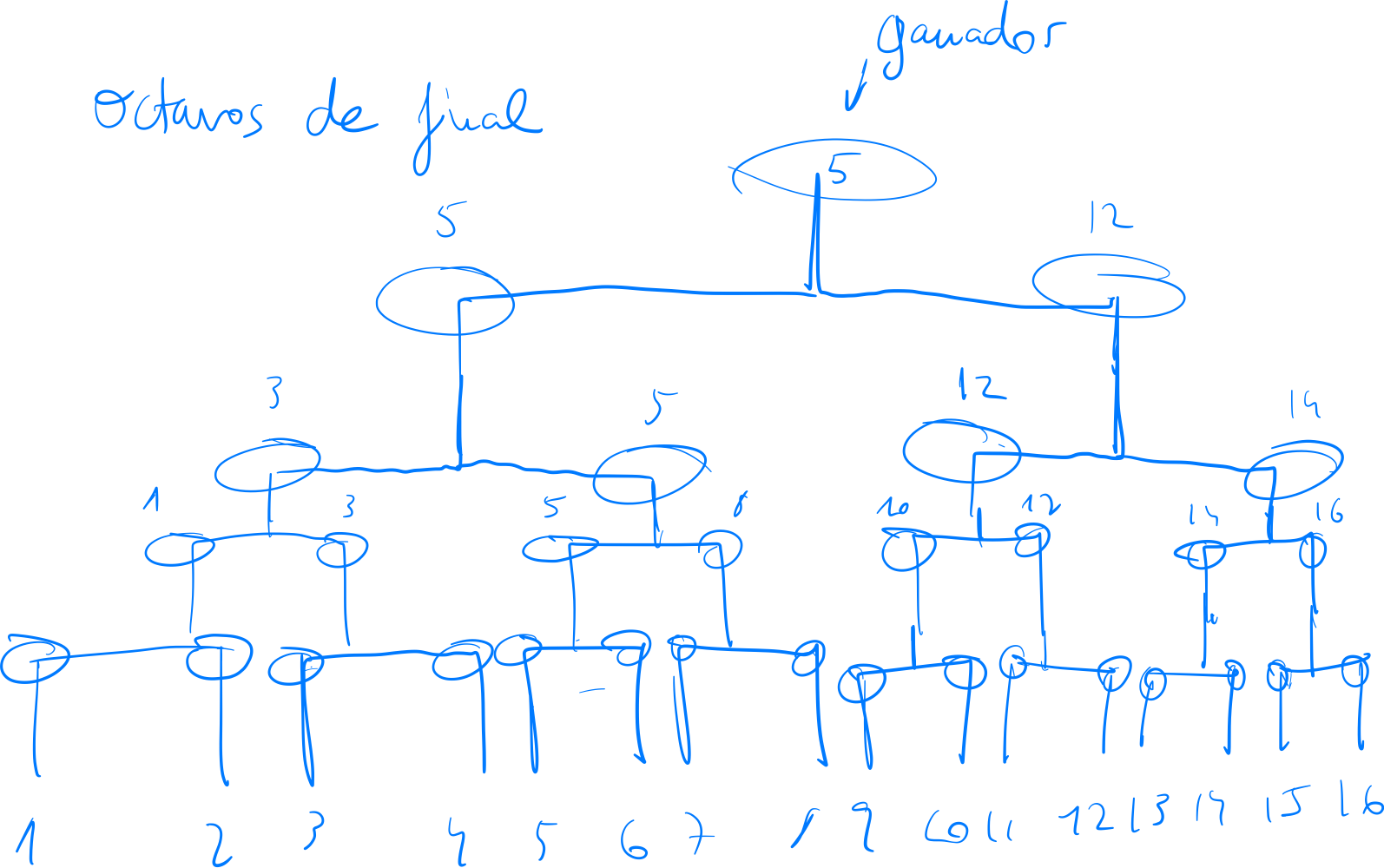
- Ejemplo de octavos de final - árbol binario
¿Qué es un árbol?
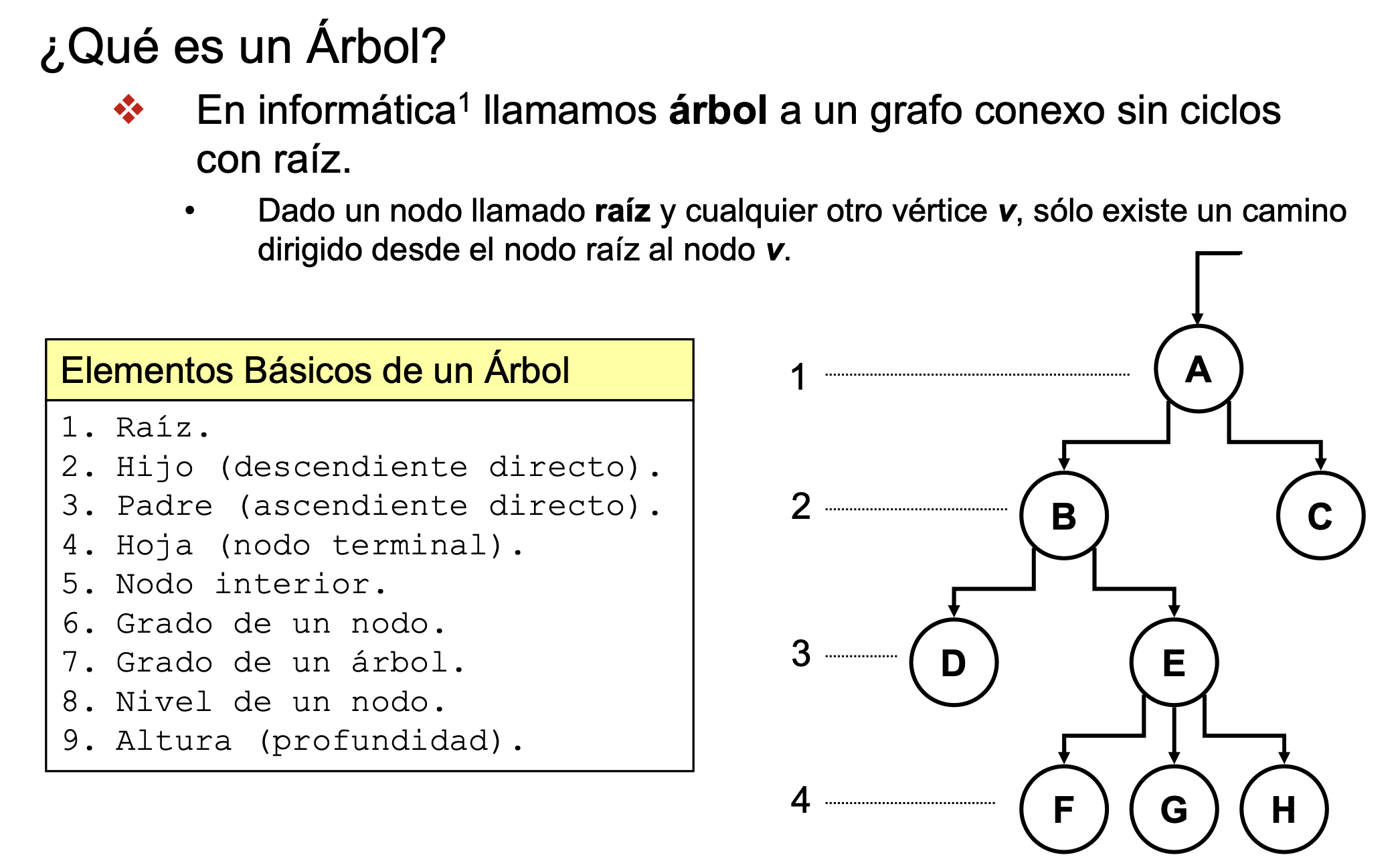
Elementos de un árbol
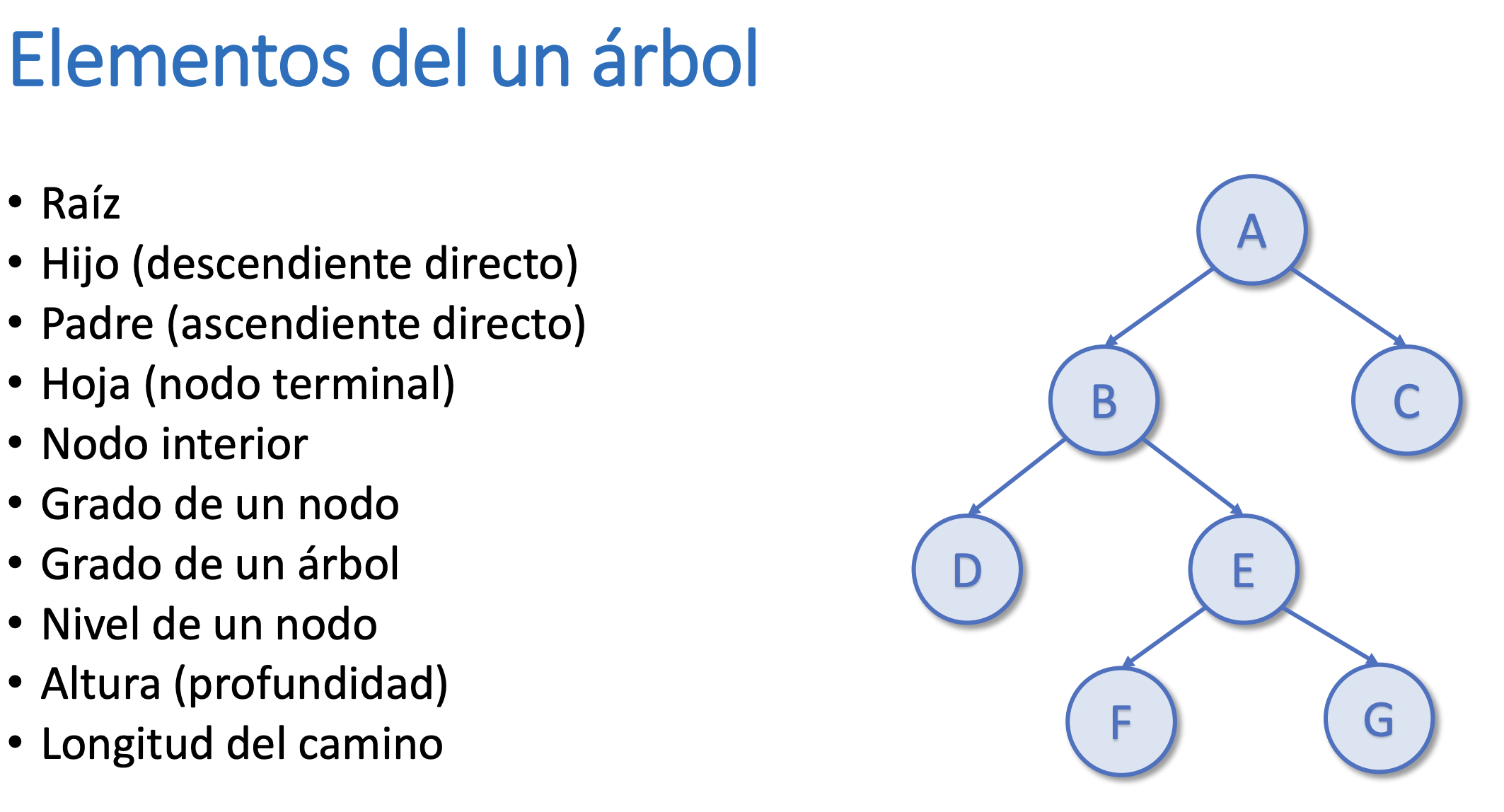
- Raíz: A
- Hijo (descendiente directo): B,C
- Padre (ascendiente directo): A, B
- Hoja (nodo terminal): D, F, G, C
- Nodo interior: B, E
- Grado de un nodo: 2
- Grado de un árbol: 2
- Nivel de un nodo: A(1), B(2), E(3), F(4)
- Altura (profundidad): 4
Árbol completo
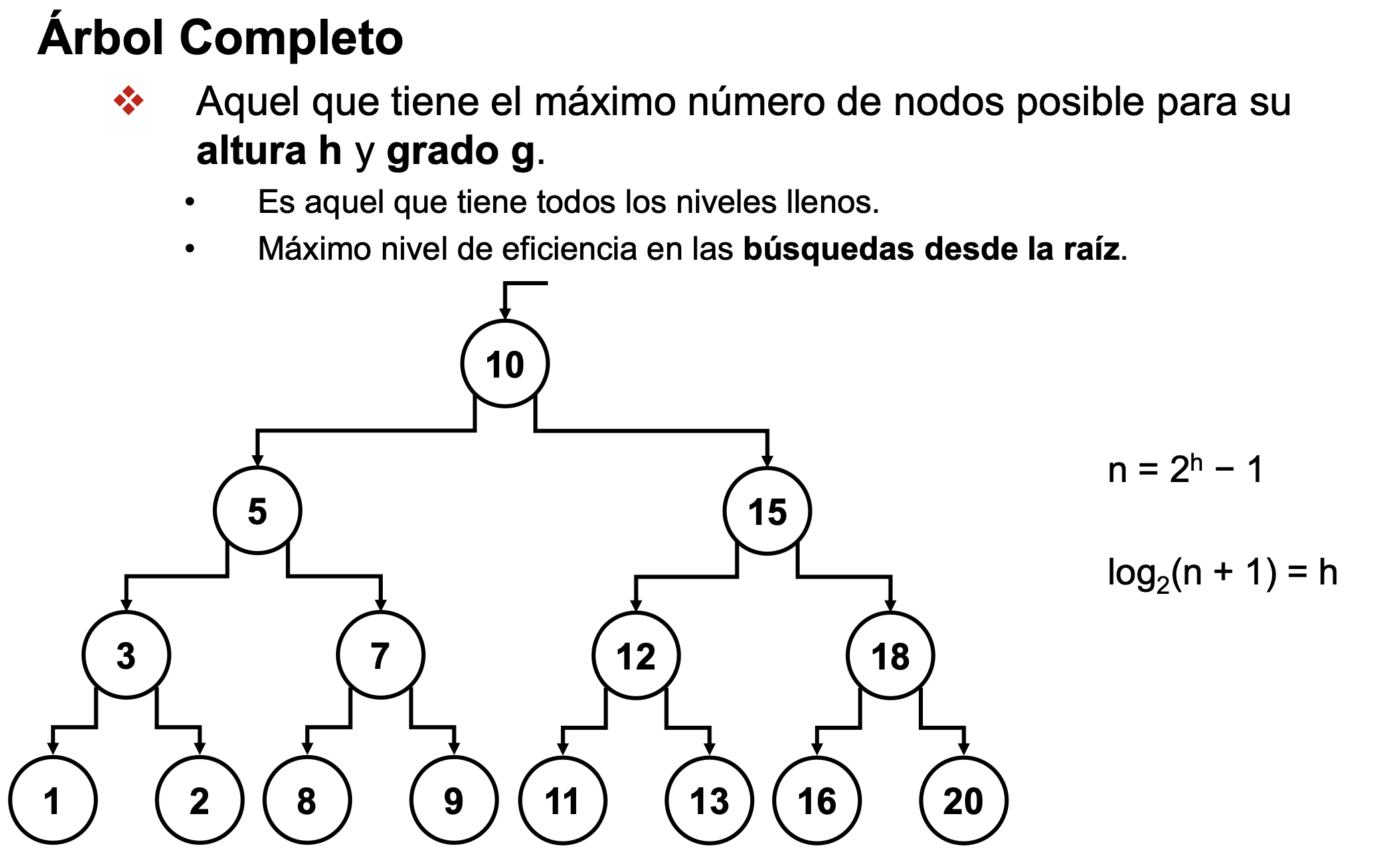
- Número medio de accesos que voy a tener que hacer es la altura (h)
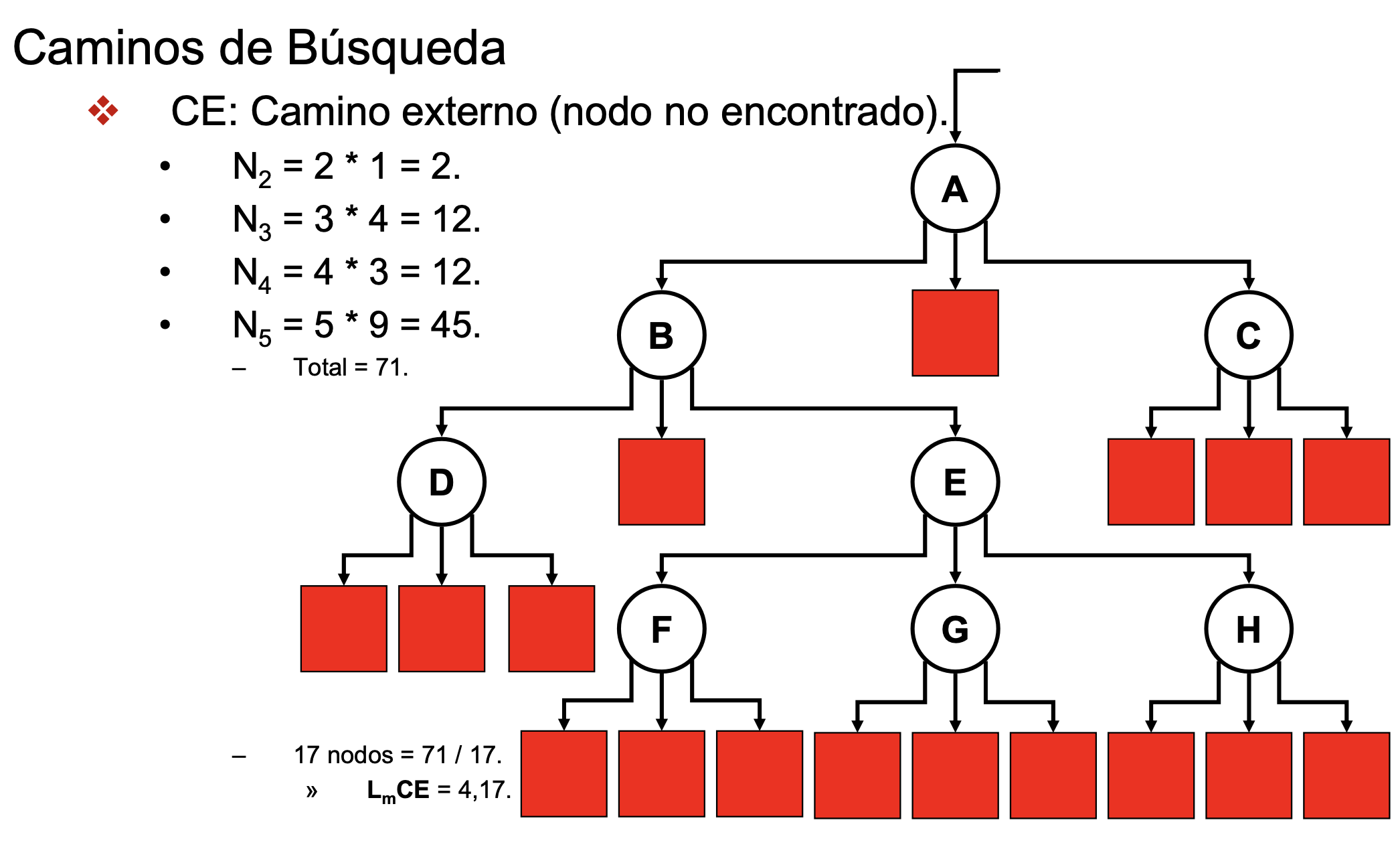
Caminos de búsqueda. Interno y Externo
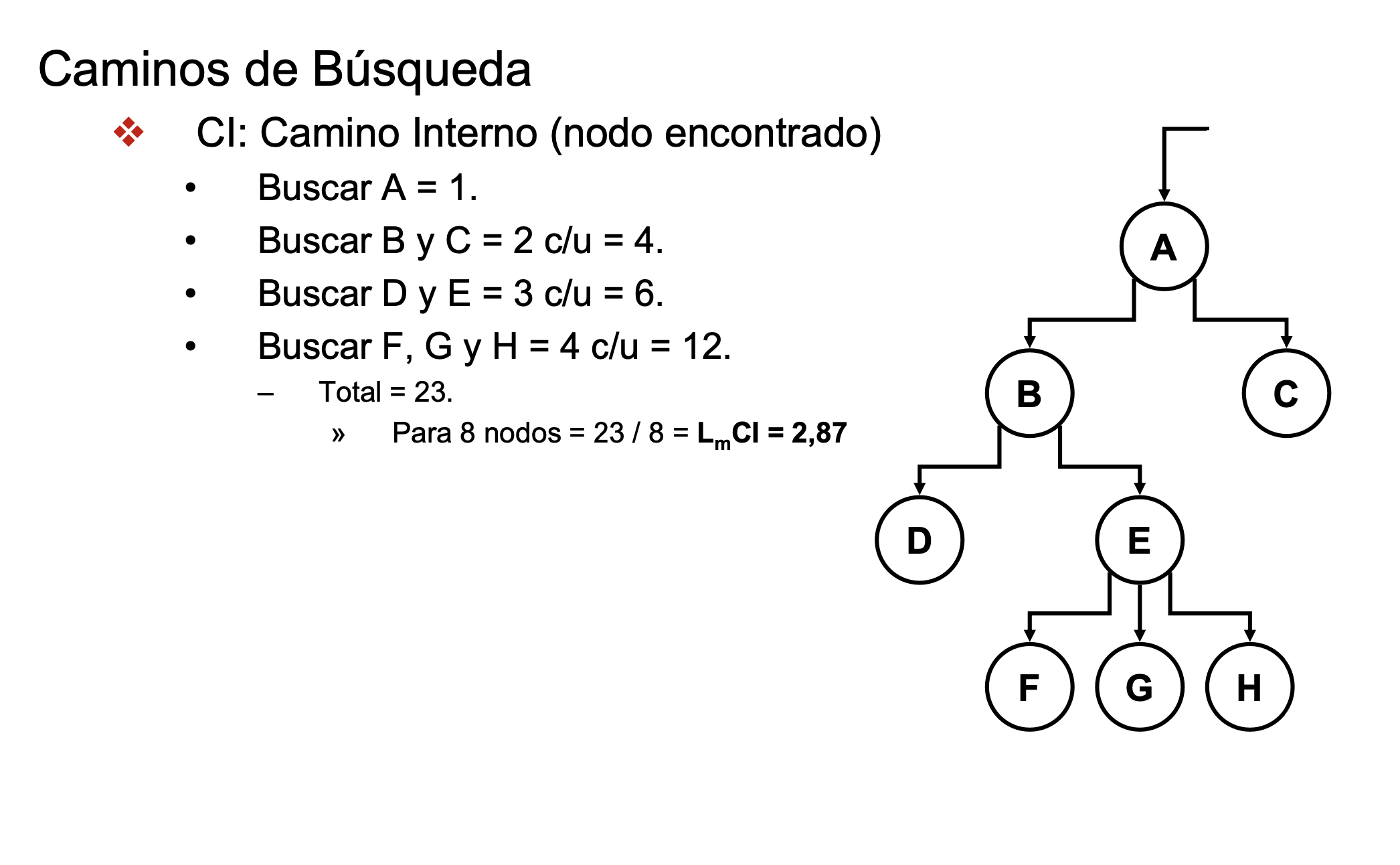
- LCI: longitud de un camino interno
Árbol Binario. Árbol de grado 2
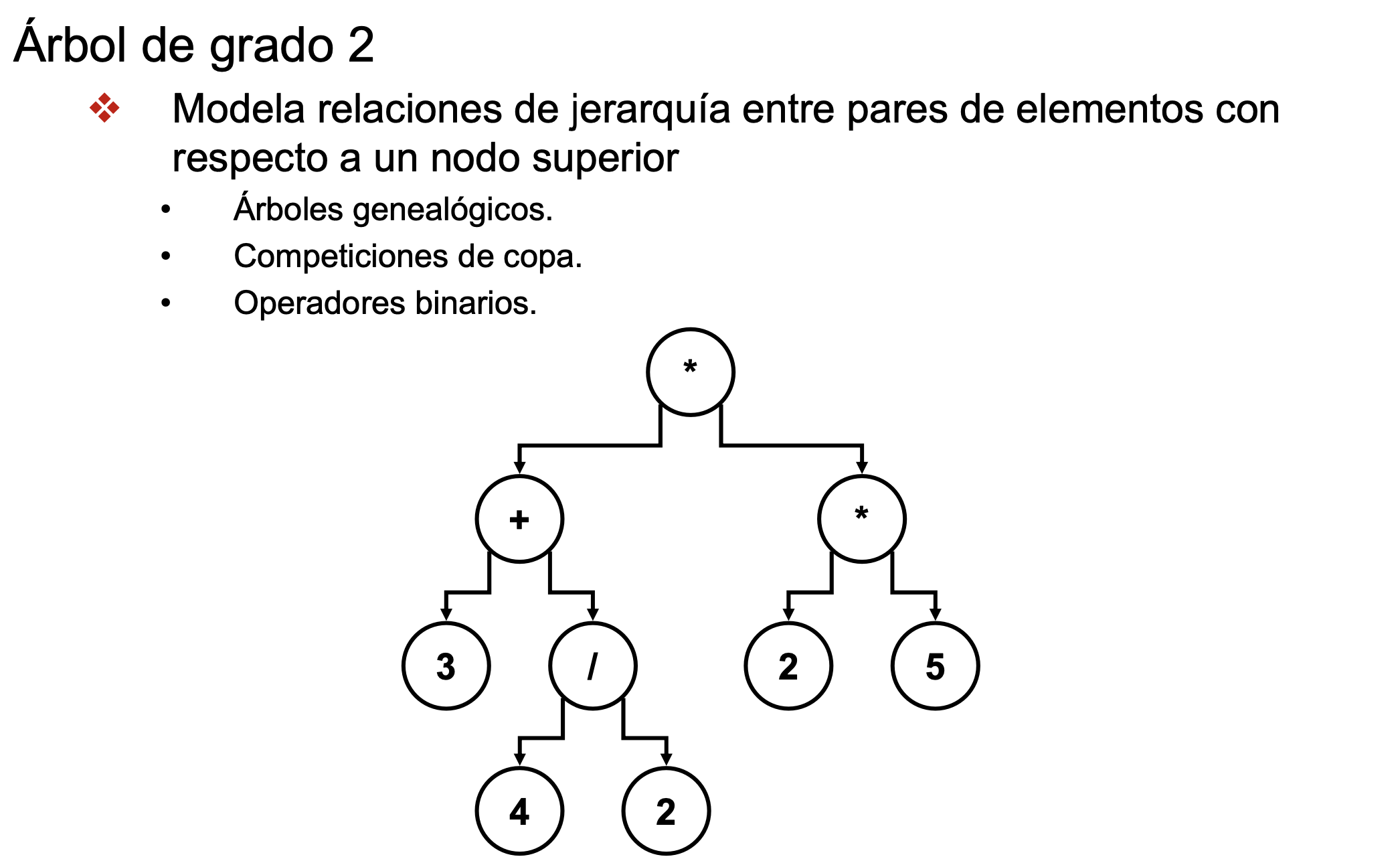
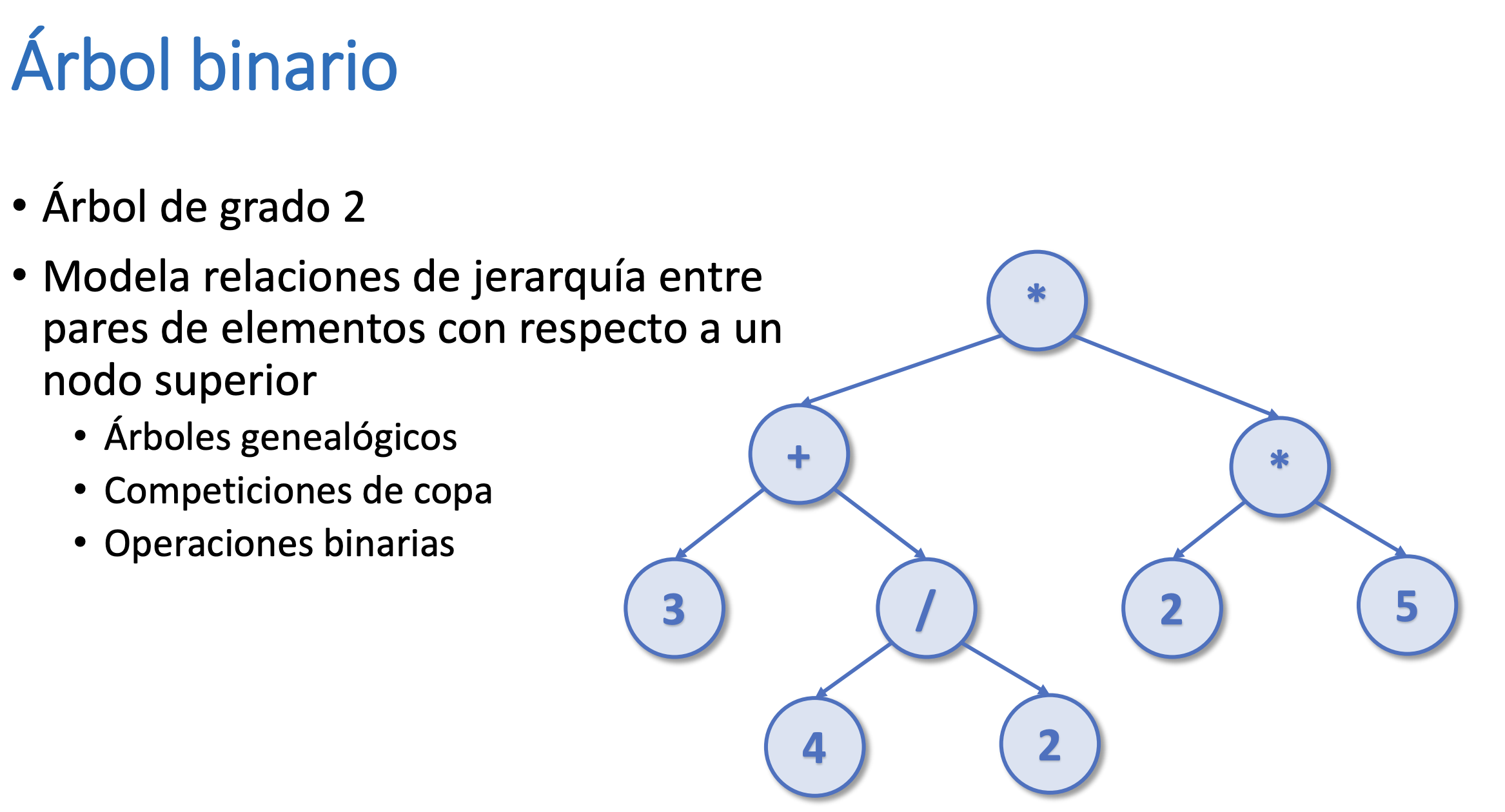
- De grado 2 significa que tiene 2 hijos
Árbol Binario Completo
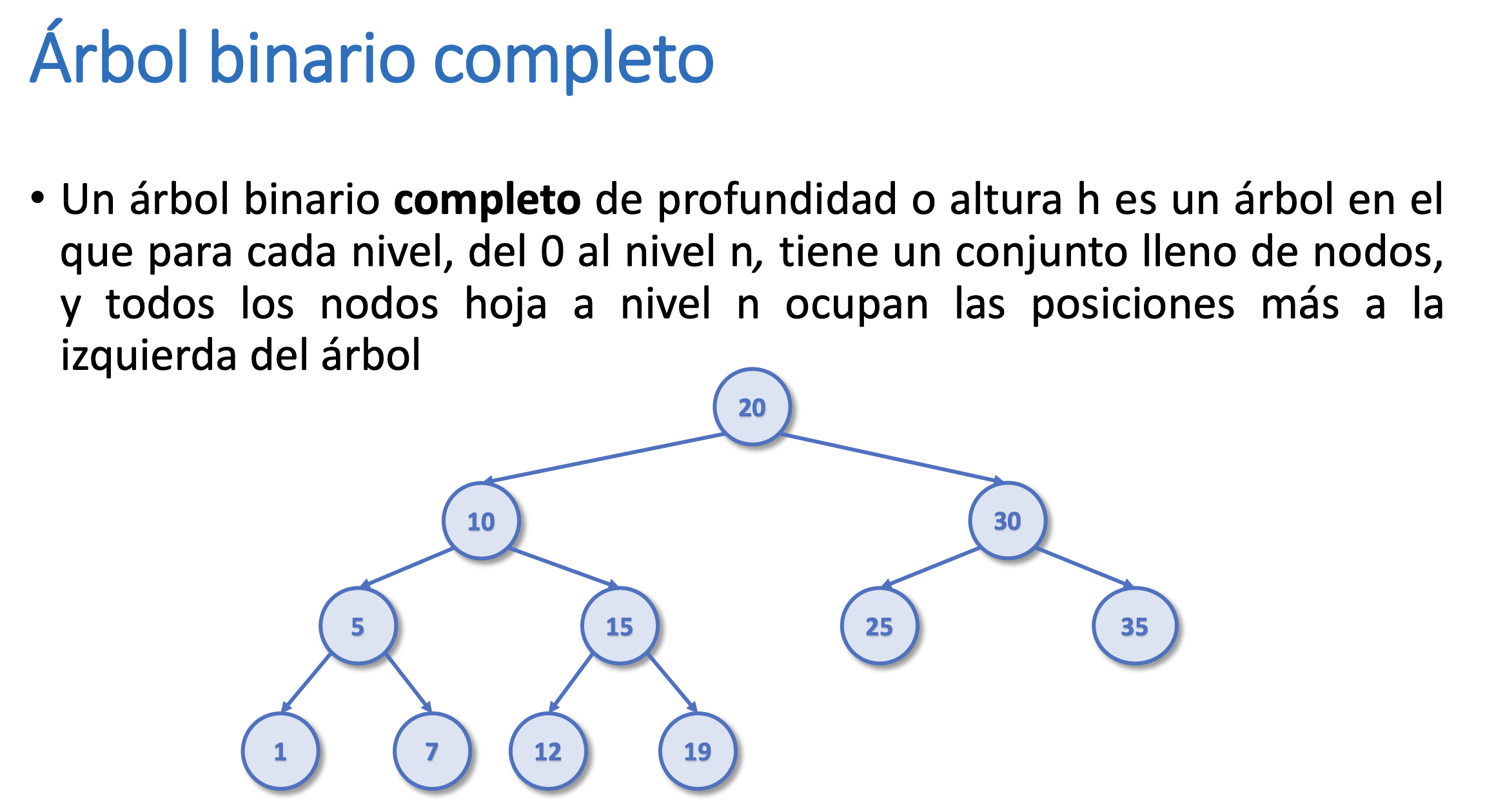
- Si quito el 12 o el 19 ya no es completo
- Si los quito a la vez sigue siendo completo
Árbol Binario lleno
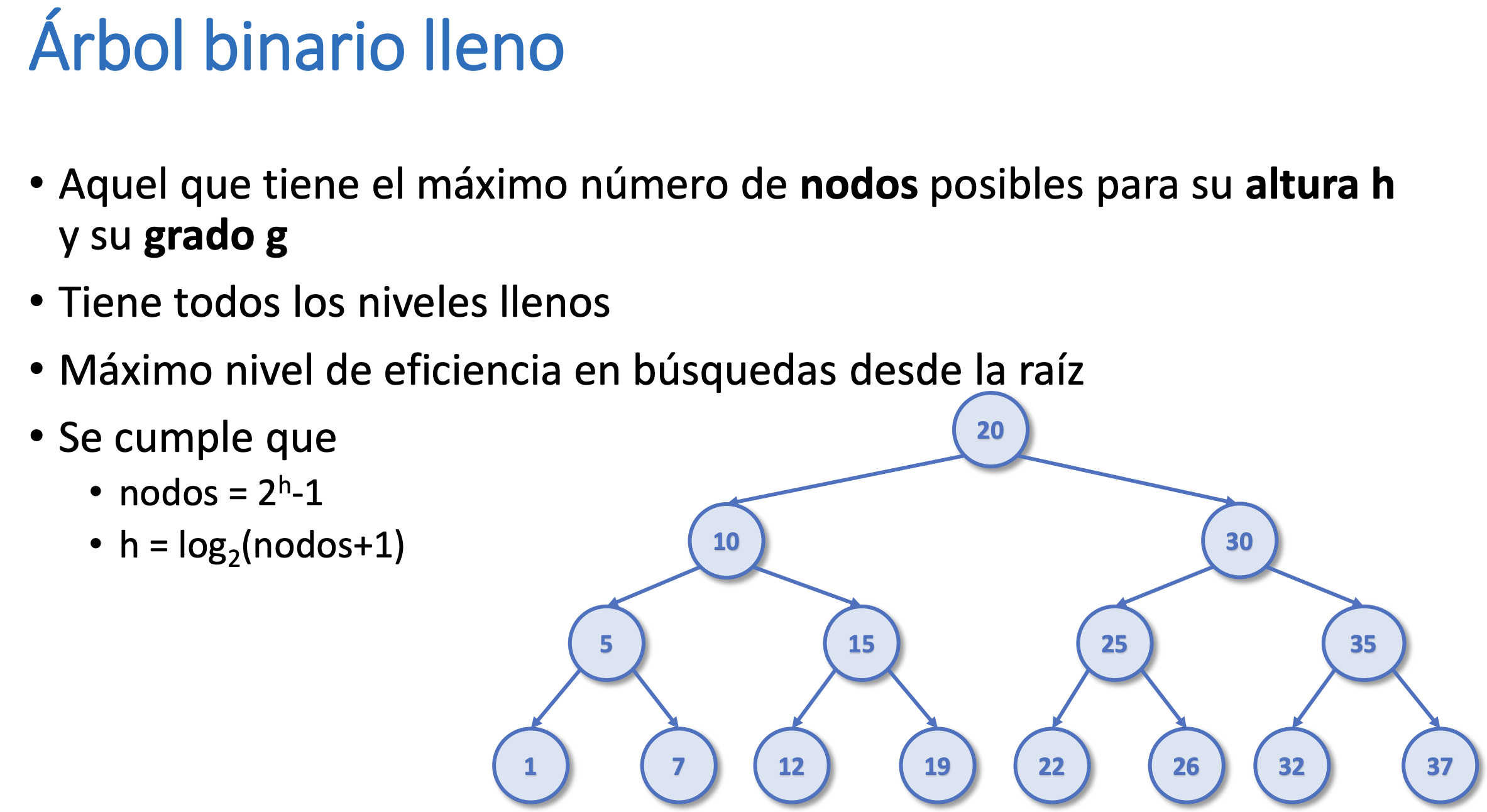
- Complejidad: log(nodos+1) (en base 2 porque el grado es 2, pero si el grado fuera más sería más)
Árbol binario degenerado

Árbol Binario de Búsqueda (ABB)
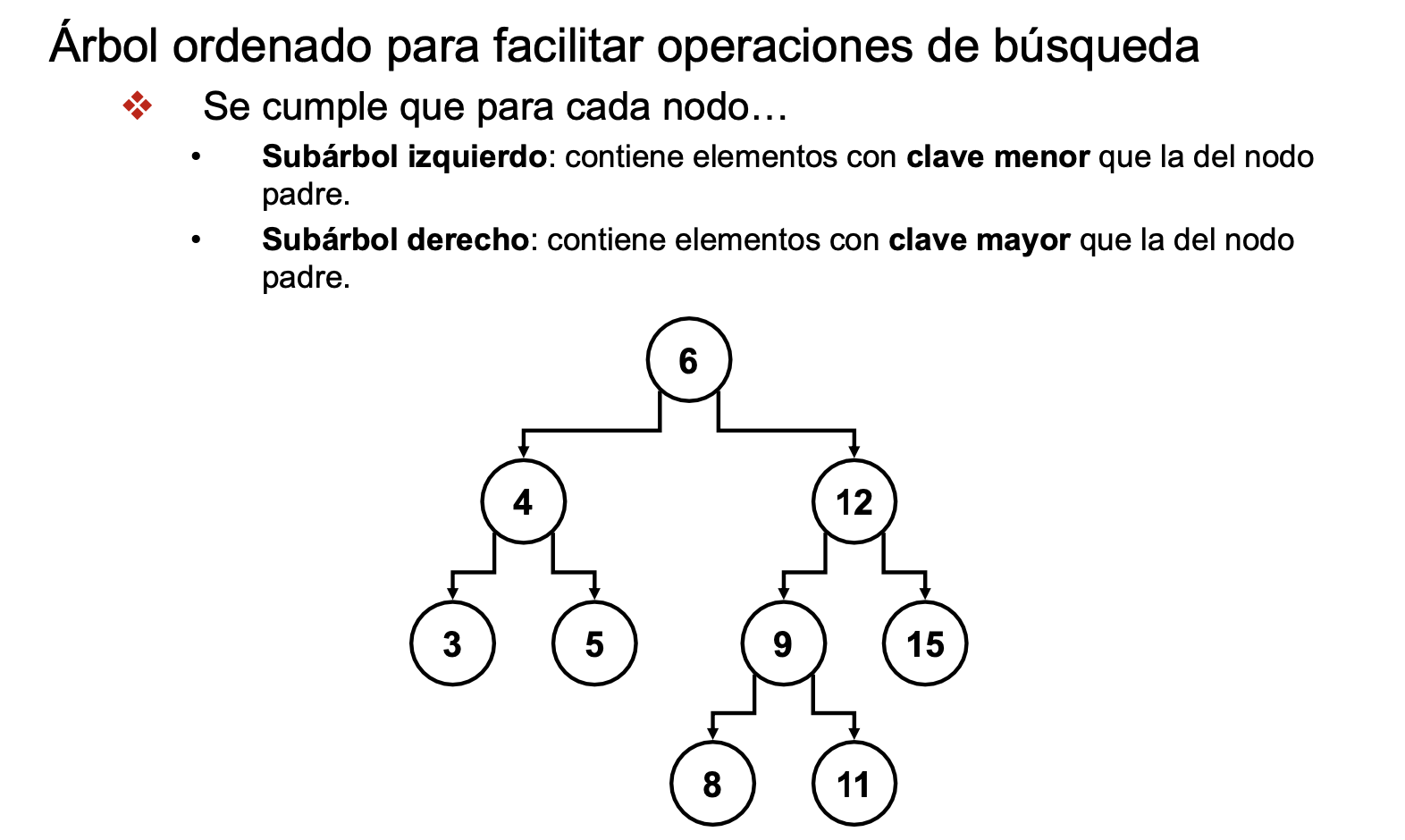
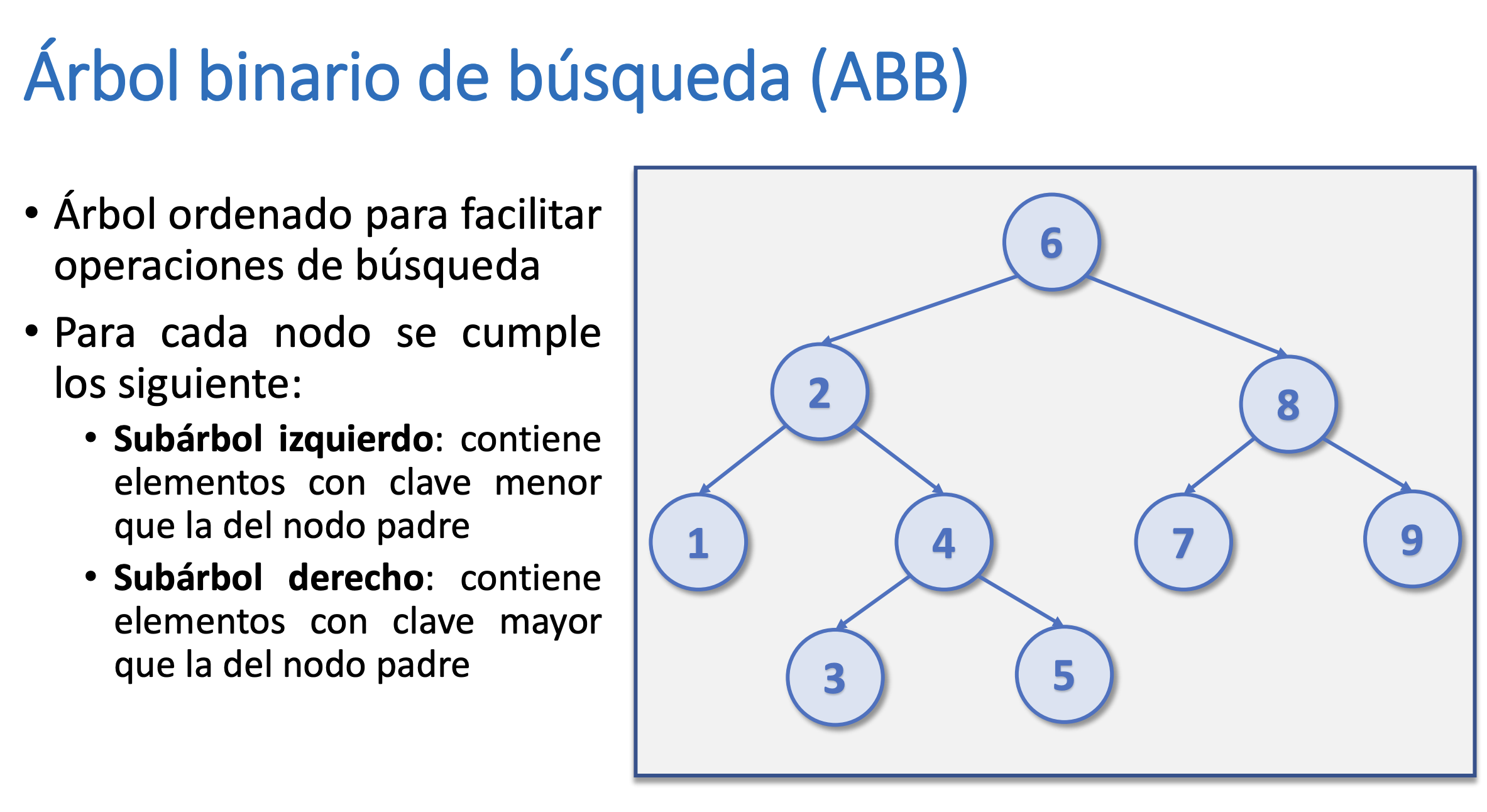
Implementación de un ABB
Estructura de datos para definir un nodo

- Lo vamos a llamar BSTNode
public class BSTNode<T extends Comparable<T>>{
private T info;
private BSTNode<T> left;
private aBSTNode<T> right;
}Estructura de datos para definir un árbol

- Lo vamos a llamar BSTree
public class BSTree<T extends Comparable<T>>{
private BSTNode<T> source;//la raíz
}Añadir un nodo al árbol

Ejercicios

1
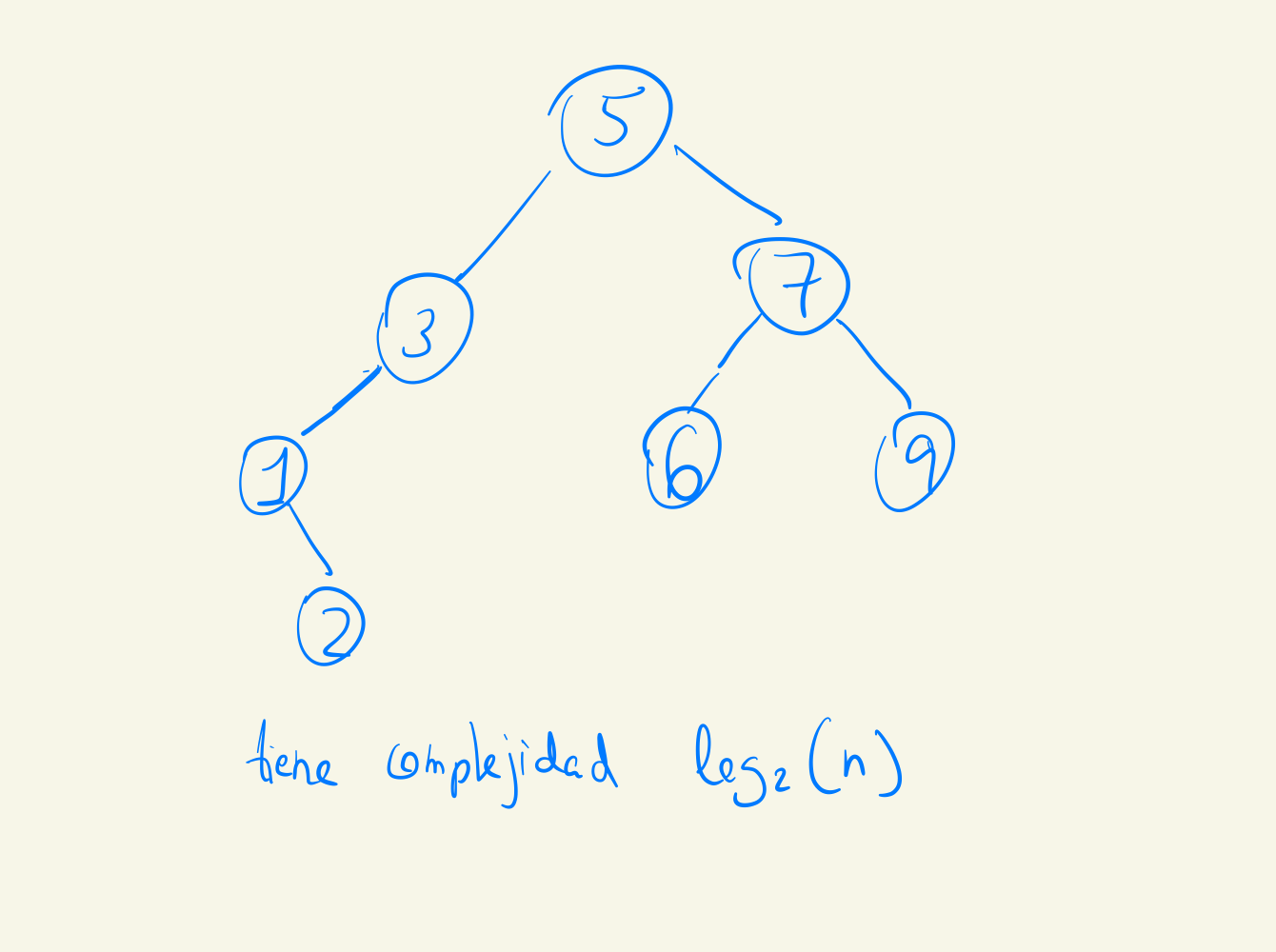
- La complejidad es esa porque depende de la altura del árbol y del número de nodos
2
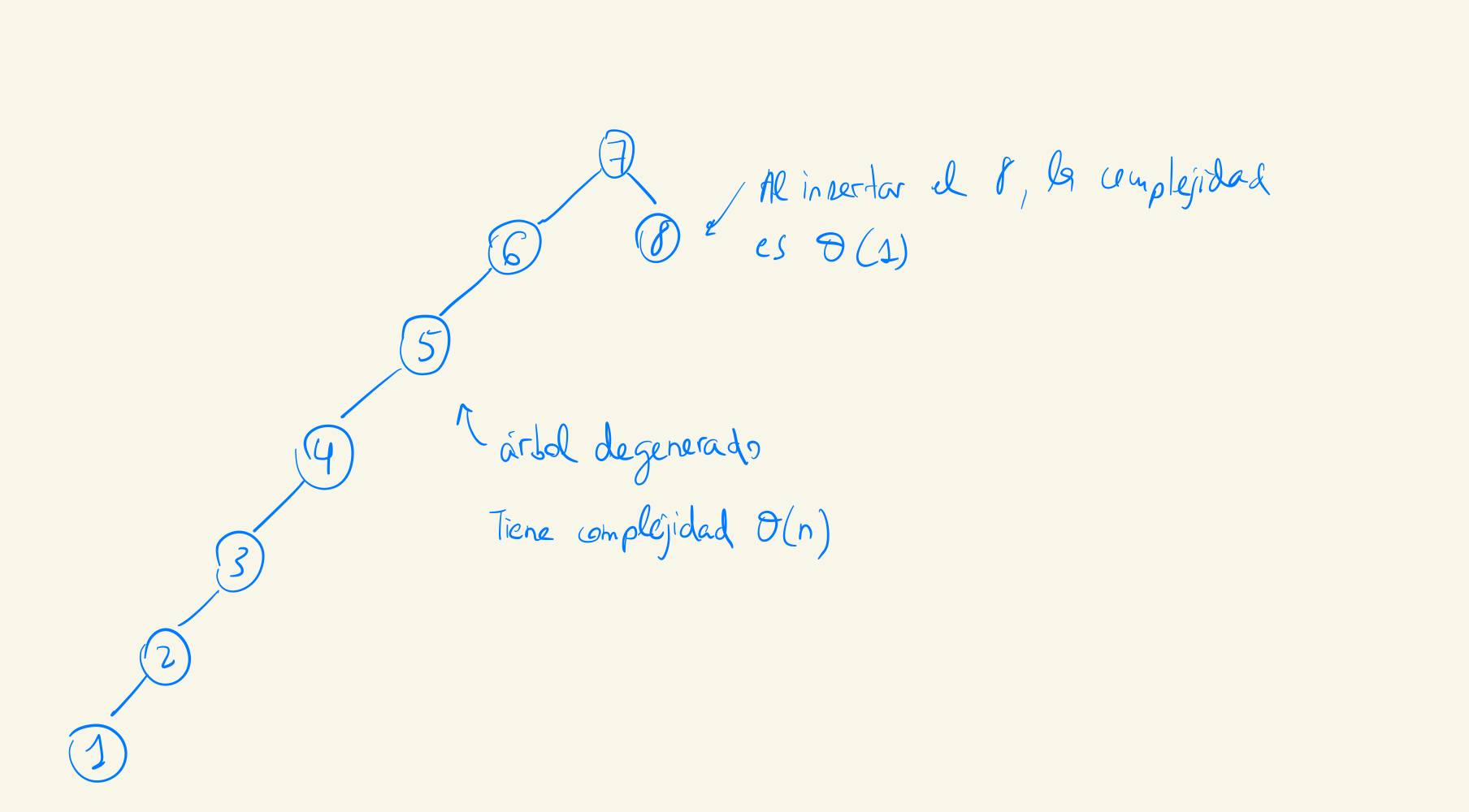
Buscar un nodo en un árbol

//Tiene complejidad log(n) en base 2
public BSTNode<T> searchNode(BSTNode<T> node){
if(this.source == null)
return null;
if(node.compareTo(this.source) == 0)
return this.source;
return searchNodeRecursive(this.source, node);
}
private BSTNode<T> searchNodeRecursive(BSTNode<T> source, BSTNode<T> target){
if(source == null)
return null;
if(source.compareTo(target) < 0)
return searchNodeRecursive(source.getLeft(), target);
else if(source.compareTo(target) > 0)
return searchNodeRecursive(source.getRight(), target);
else
return source;
}Eliminar un nodo del árbol

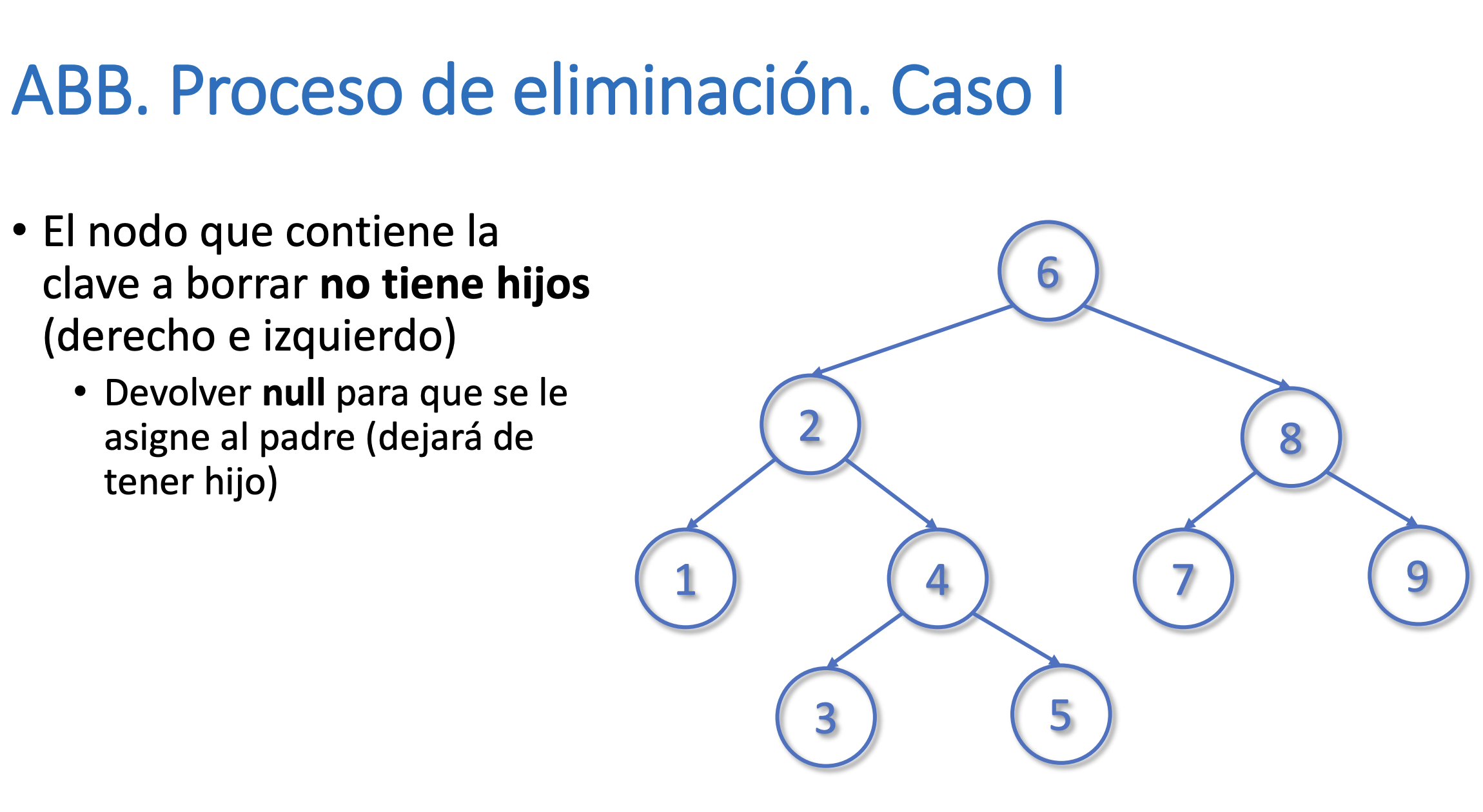
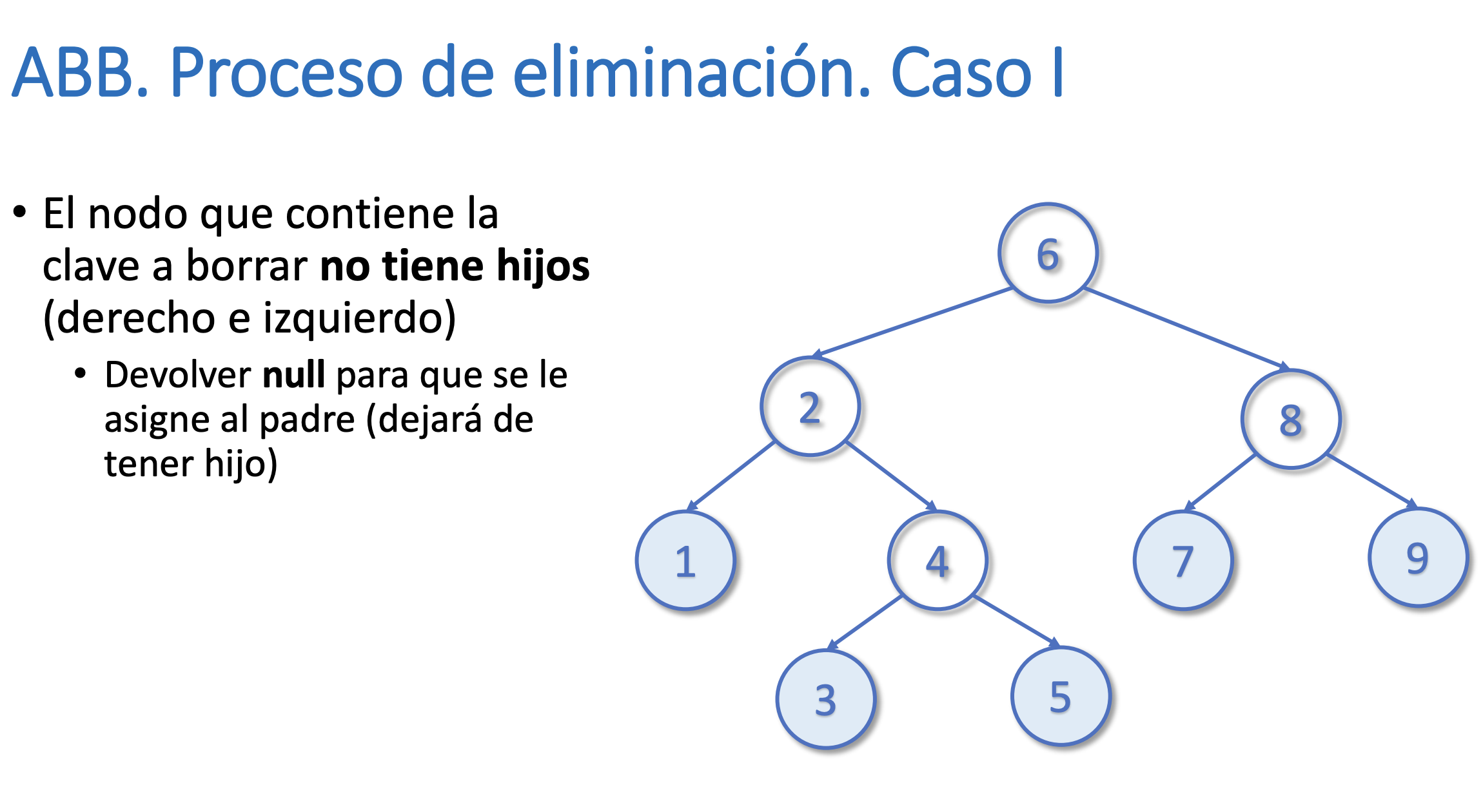
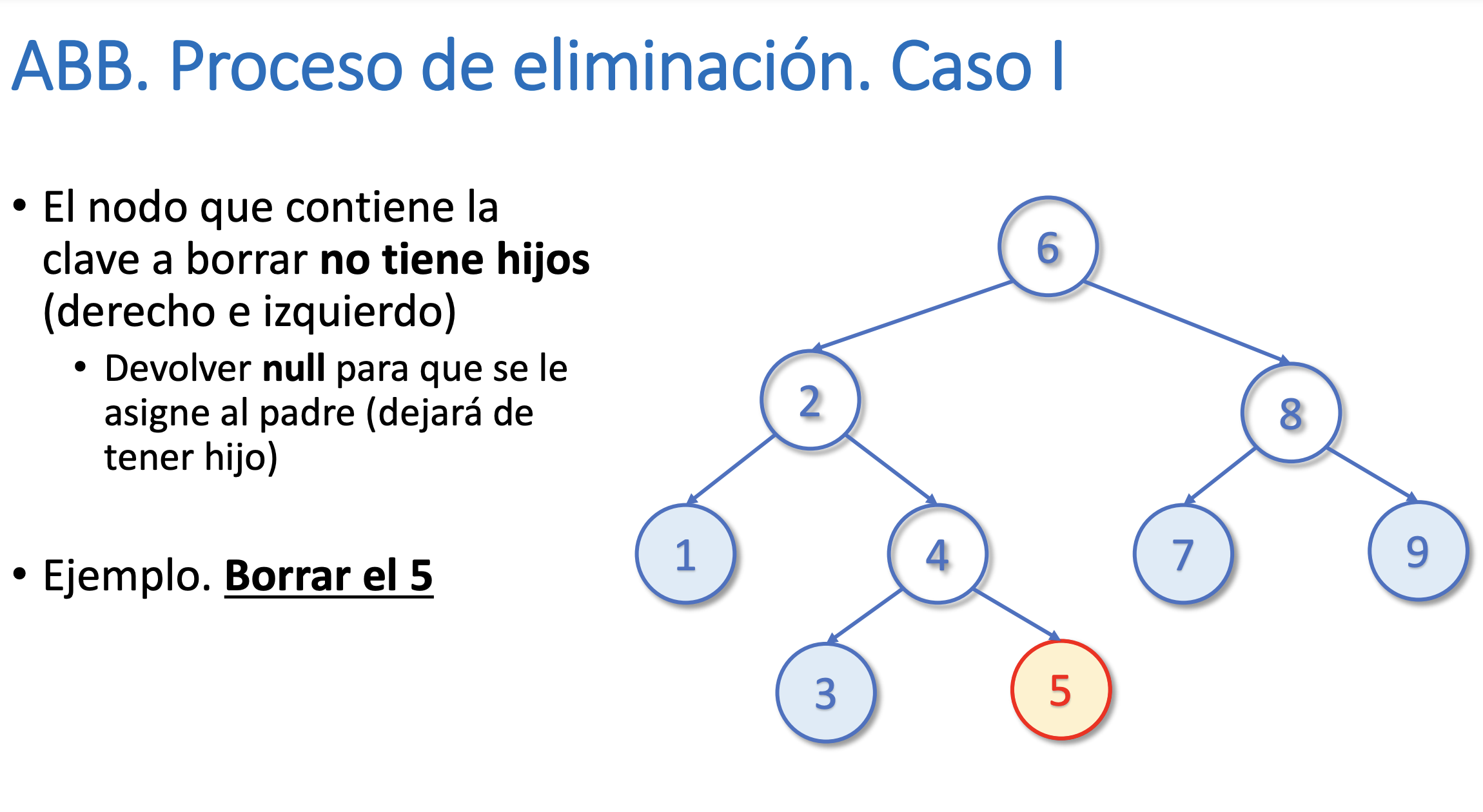
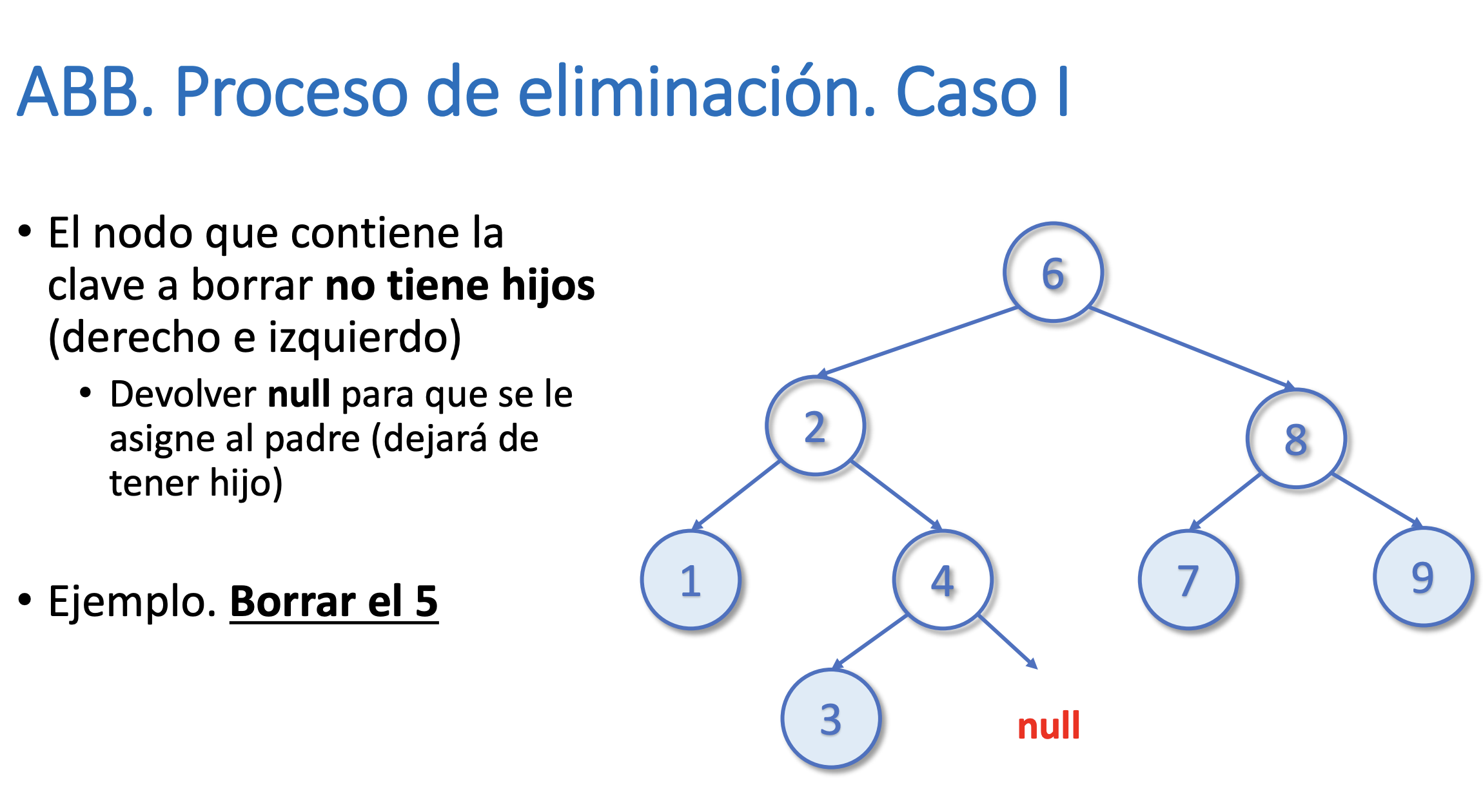
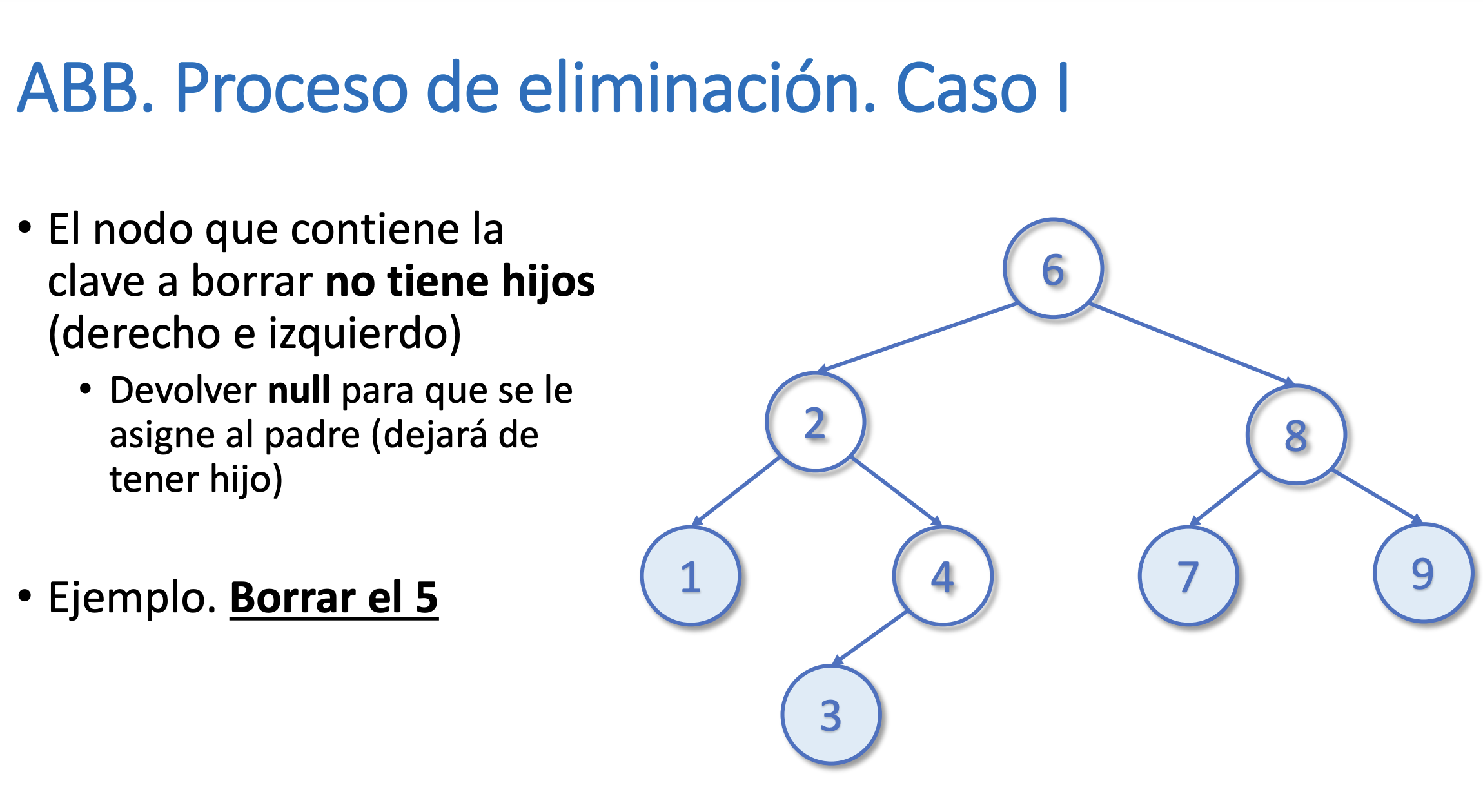
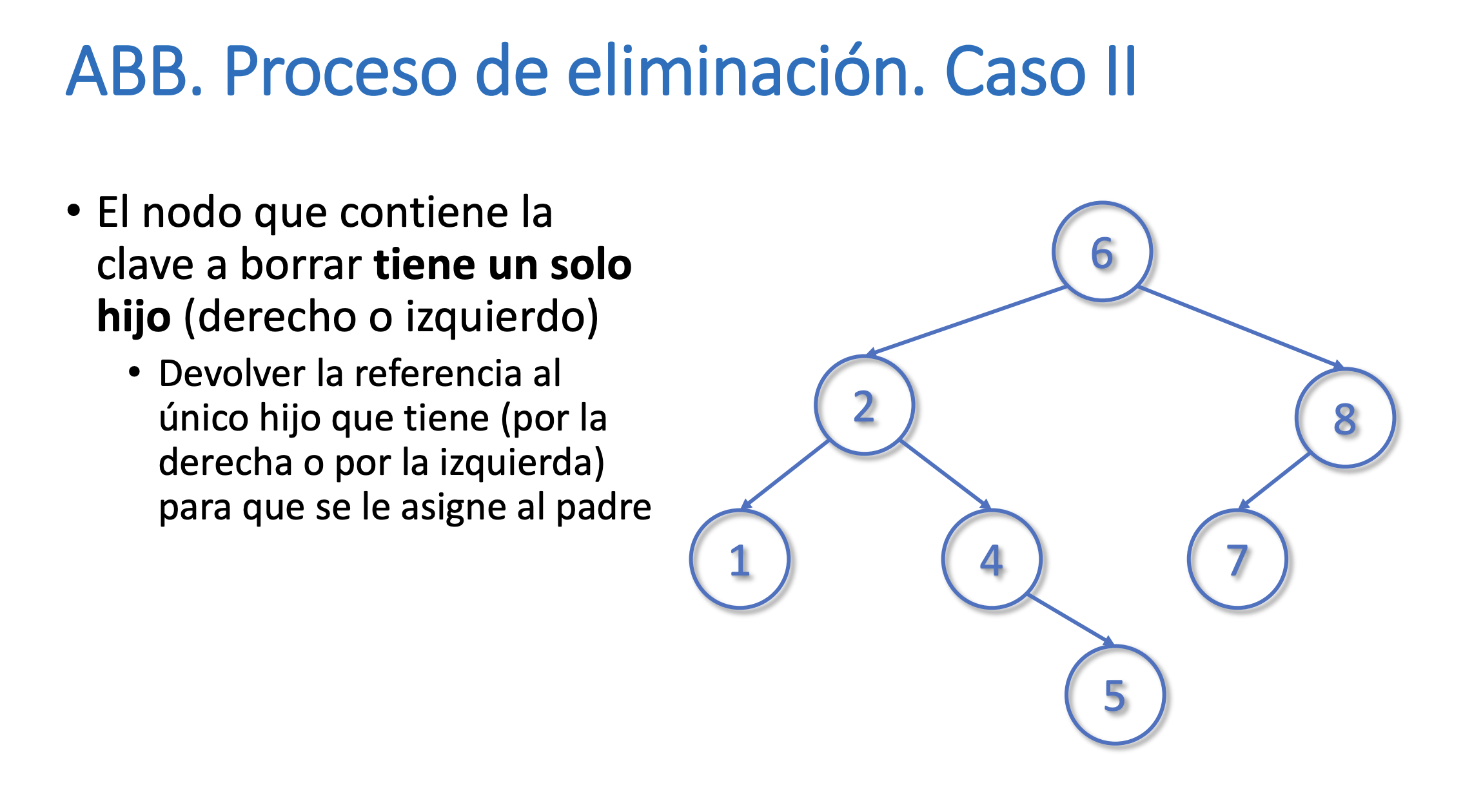
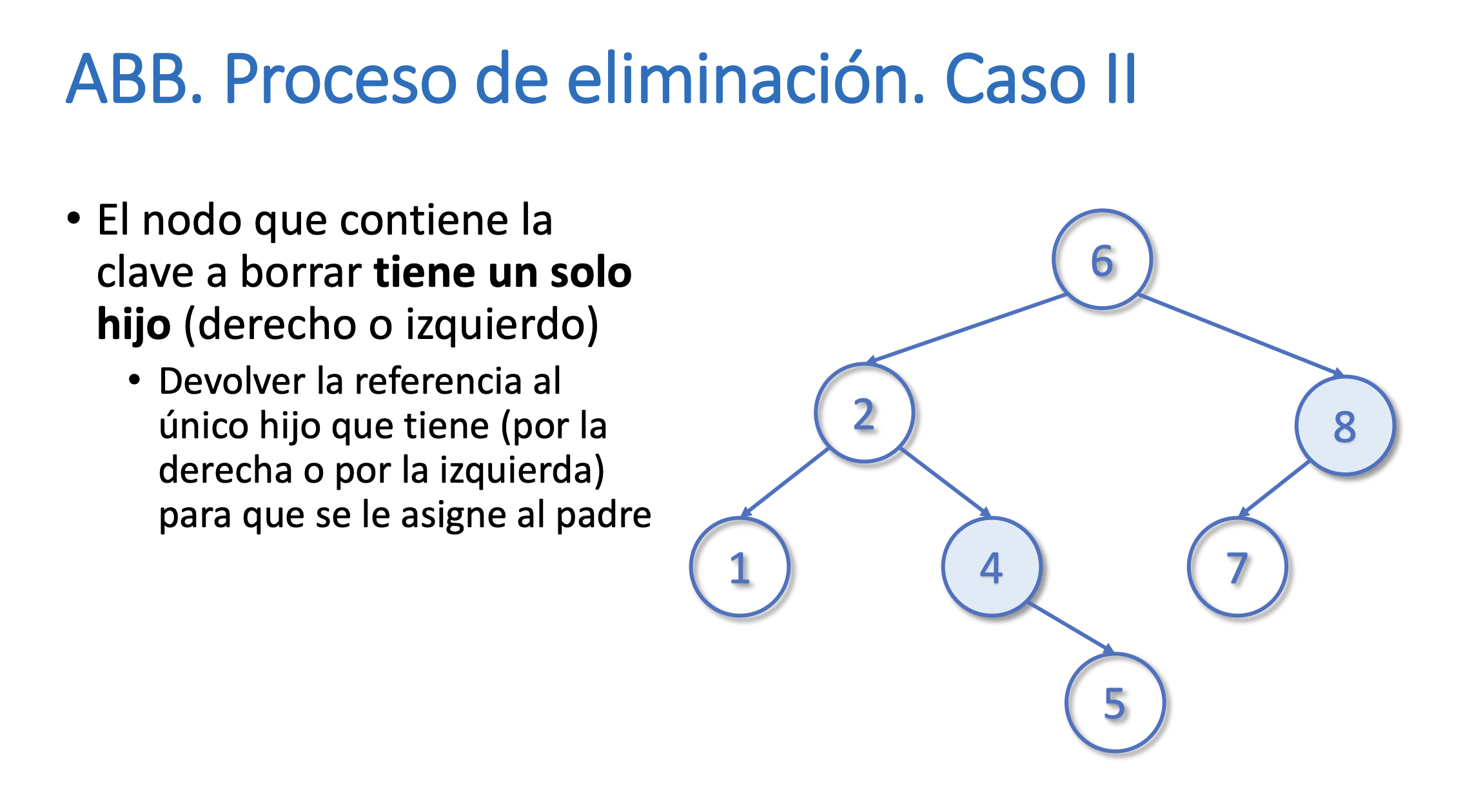
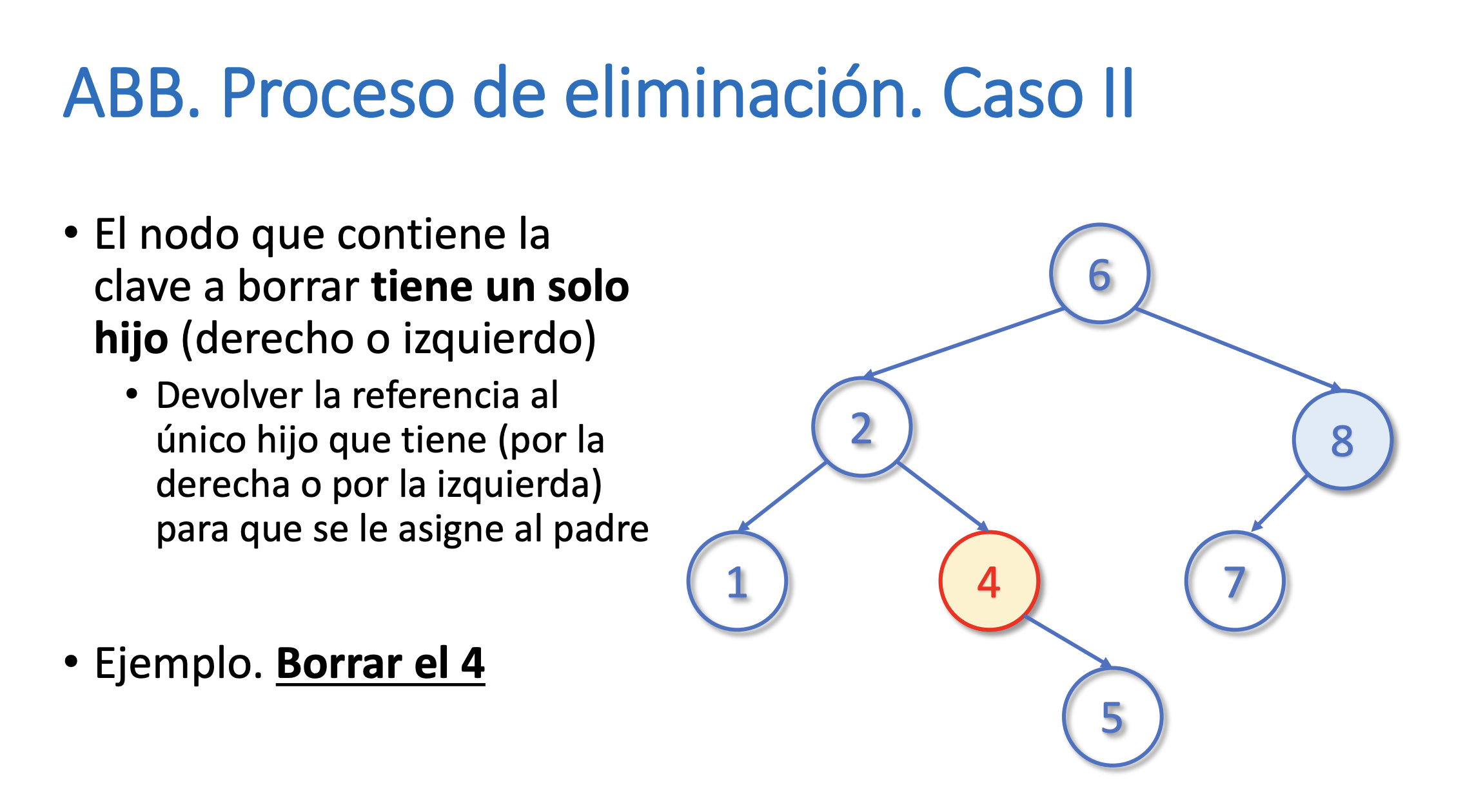
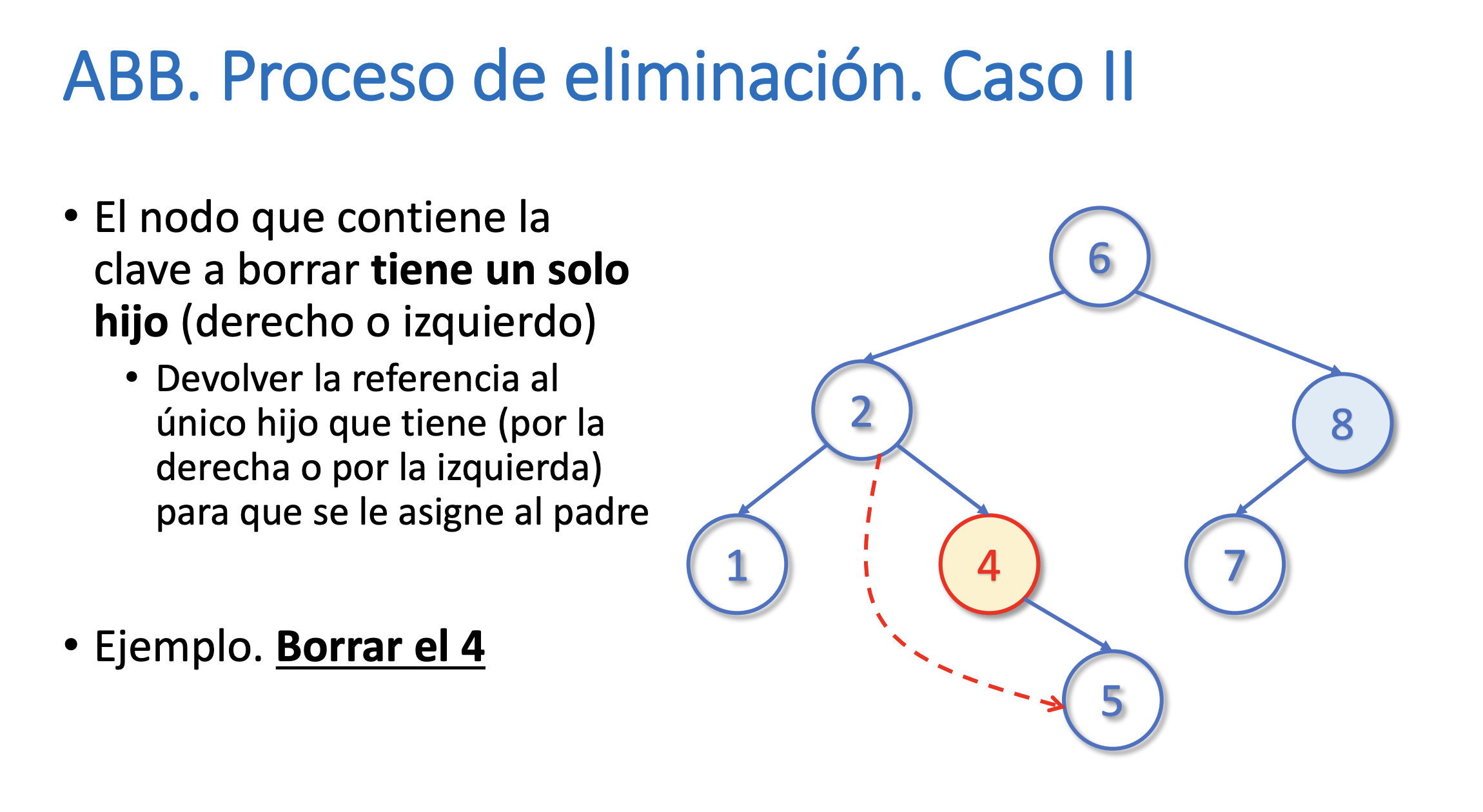
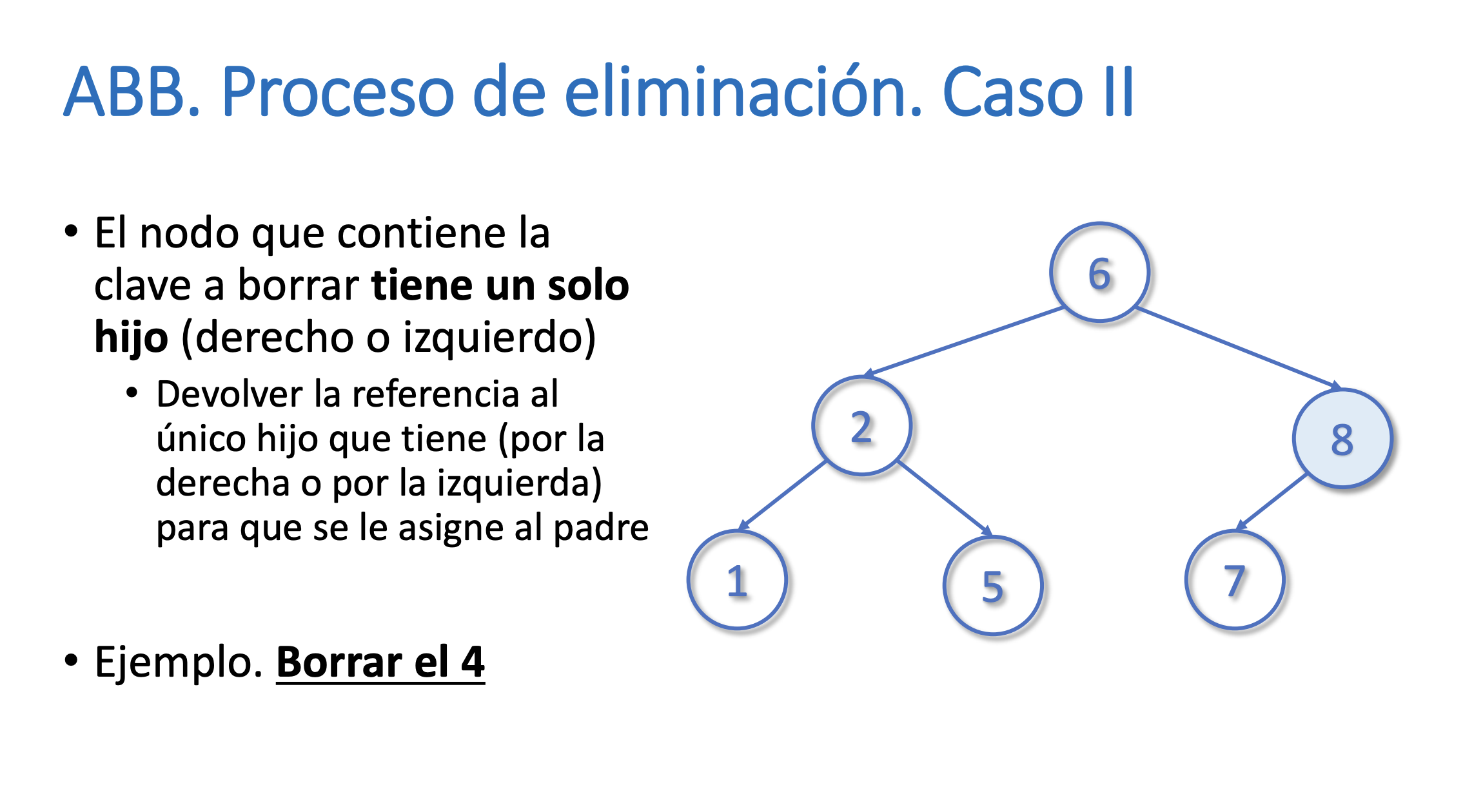
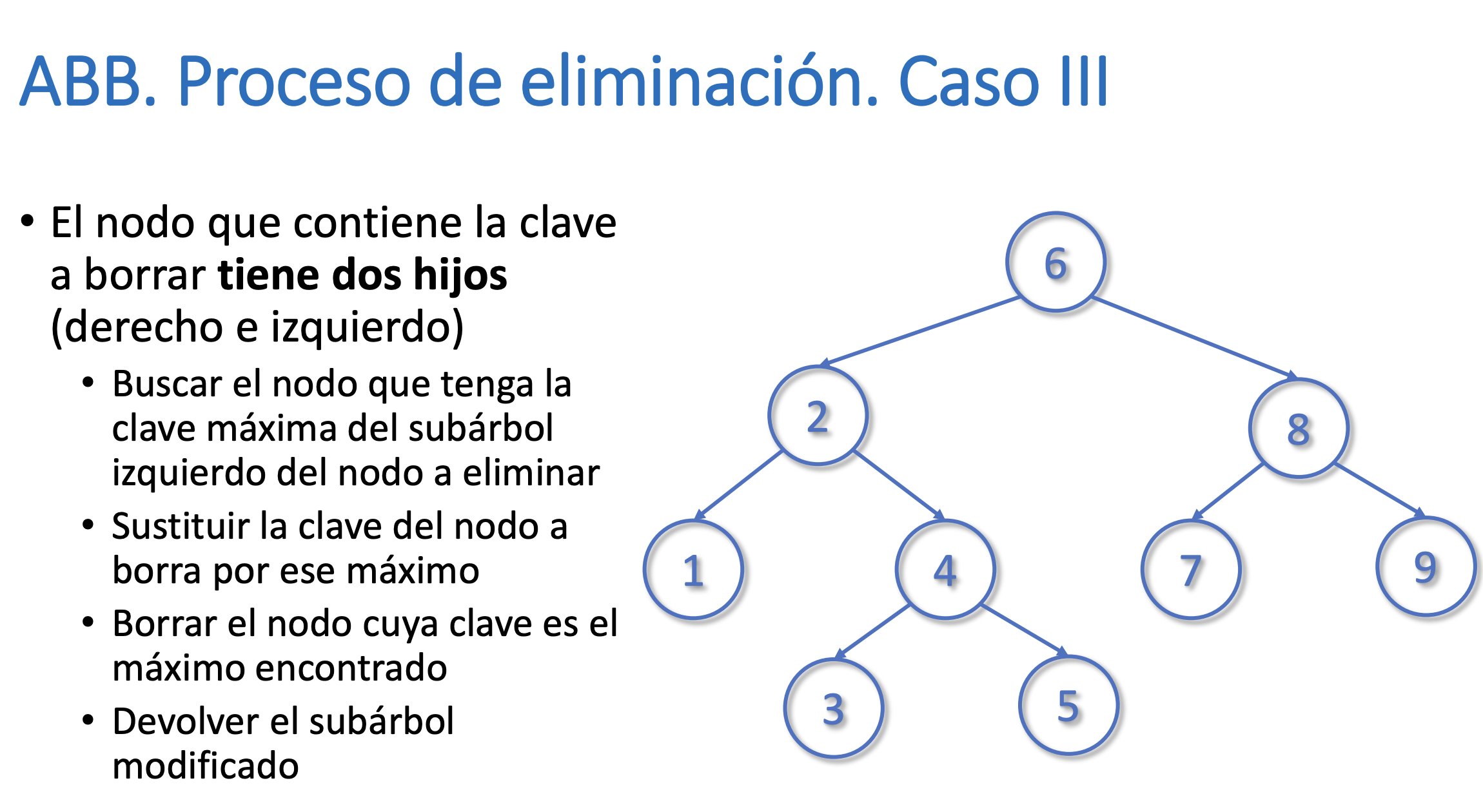
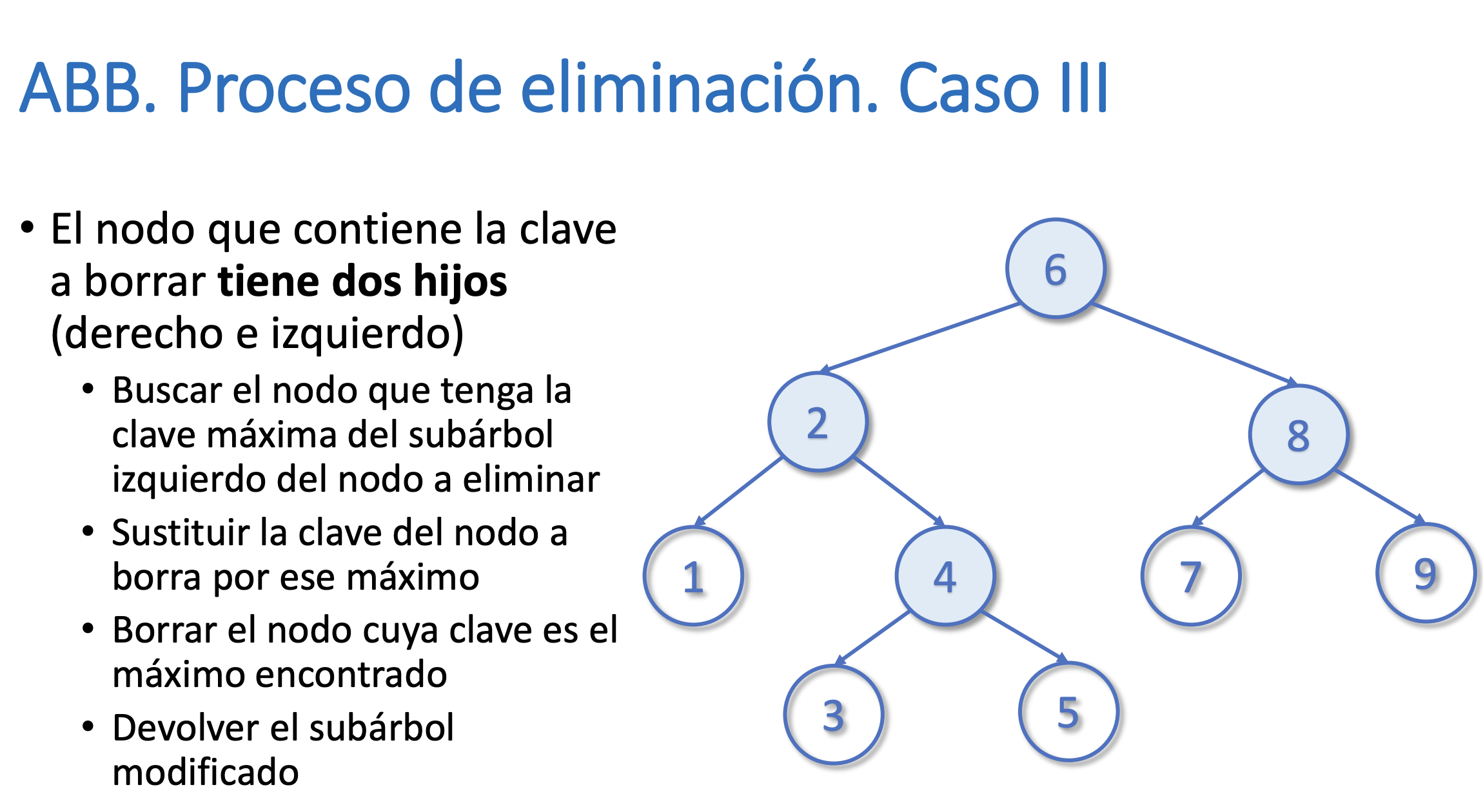
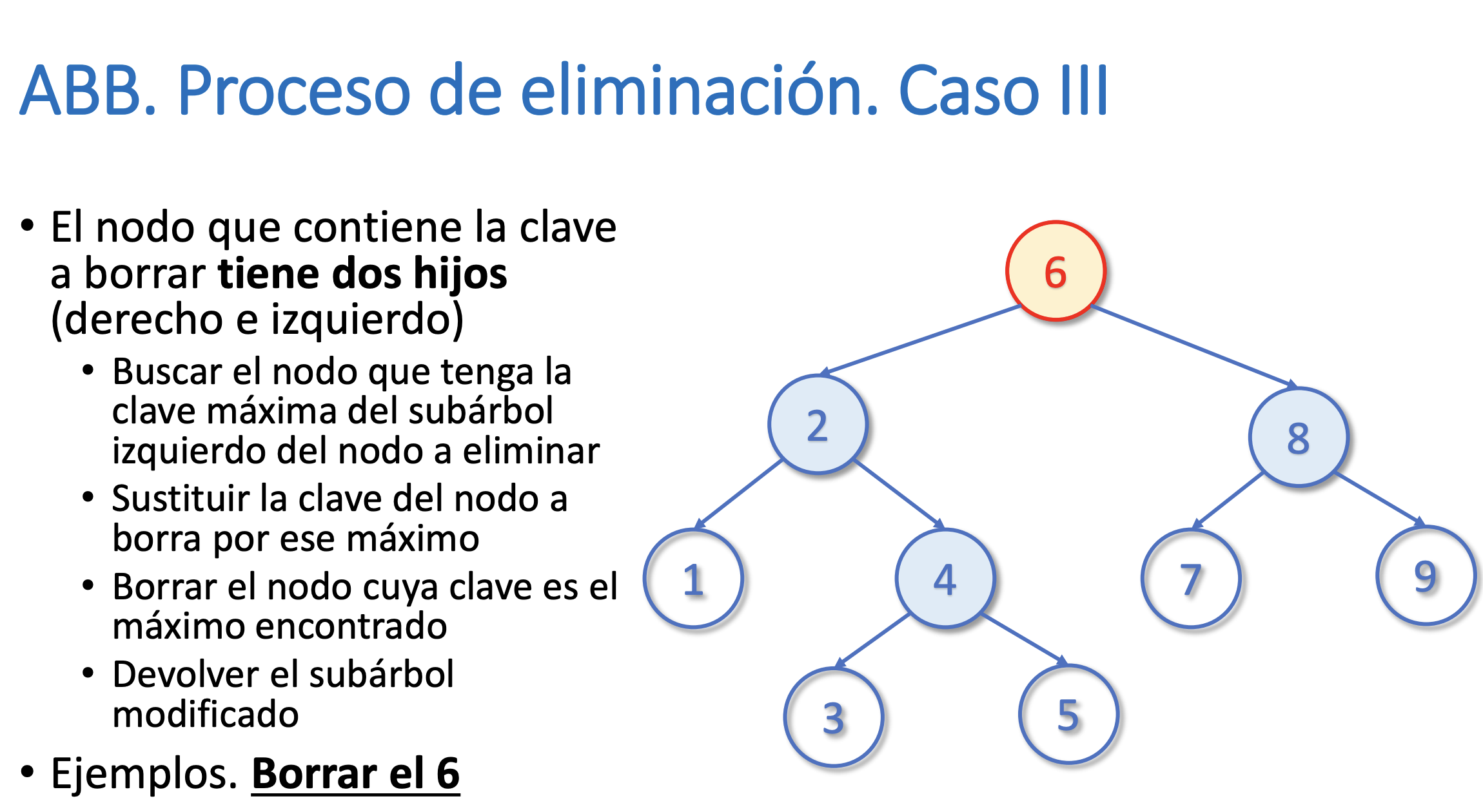
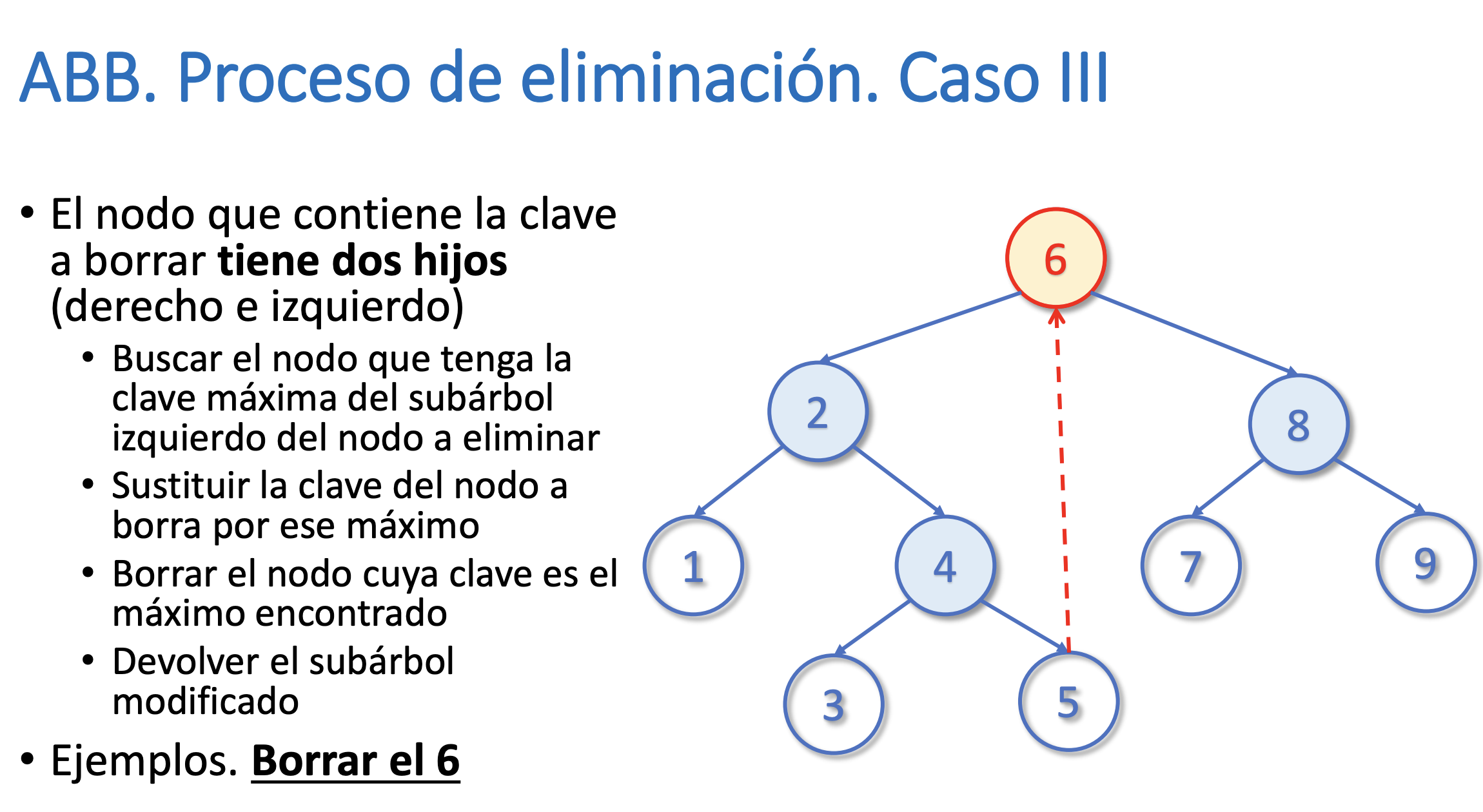
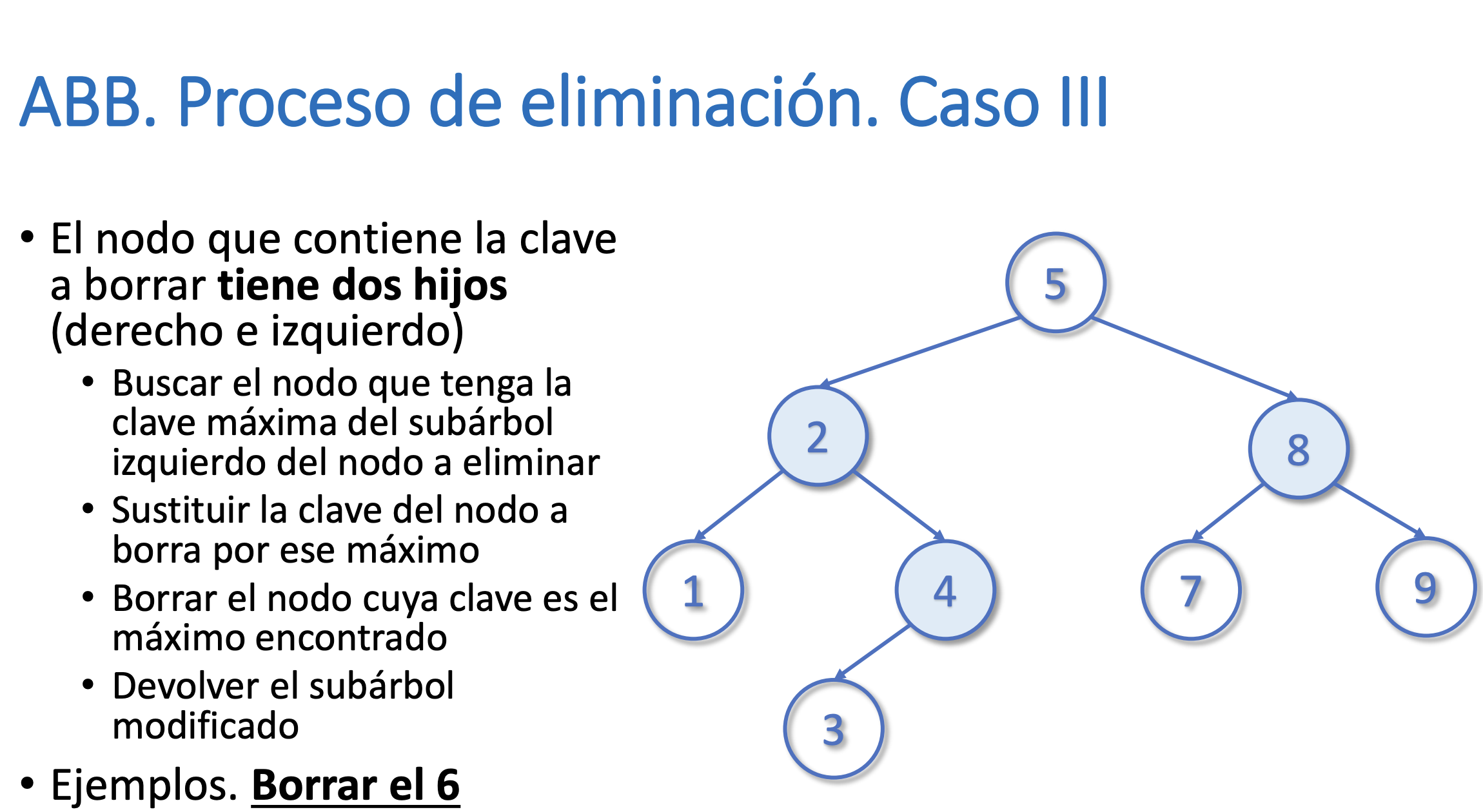
Buscar el máximo

public T buscarMaximo(BSTNode node){
if(node == null)
return null;
if(node.getRight() == null)
return node.info;
return buscarMaximo(node.getRight());
}Recorridos
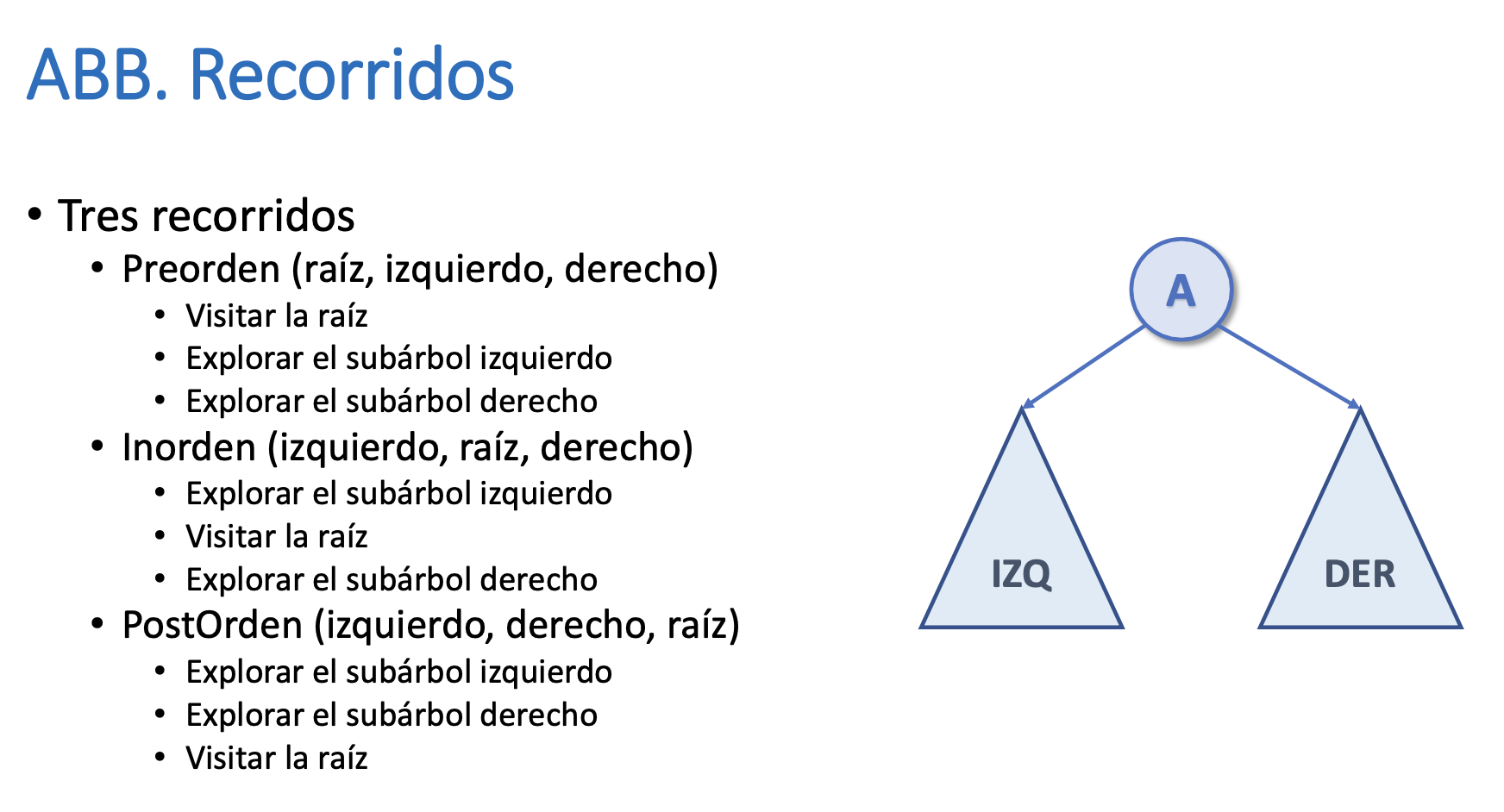
Recorridos. Ejercicios

public String preOrder() {
String cadena = recorridoPreOrderRecursivo(this.raiz);
return cadena.substring(0, cadena.length() - 1);
}
private String recorridoPreOrderRecursivo(BSTNode<T> nodoraiz) {
if (nodoraiz == null)// si la raíz es nula devolverá la cadena vacía
return "";
String cadena = nodoraiz.getInfo().toString();
cadena += "\t";
cadena += recorridoPreOrderRecursivo(nodoraiz.getLeft());
cadena += recorridoPreOrderRecursivo(nodoraiz.getRight());
return cadena;
}ABB Eficiencia

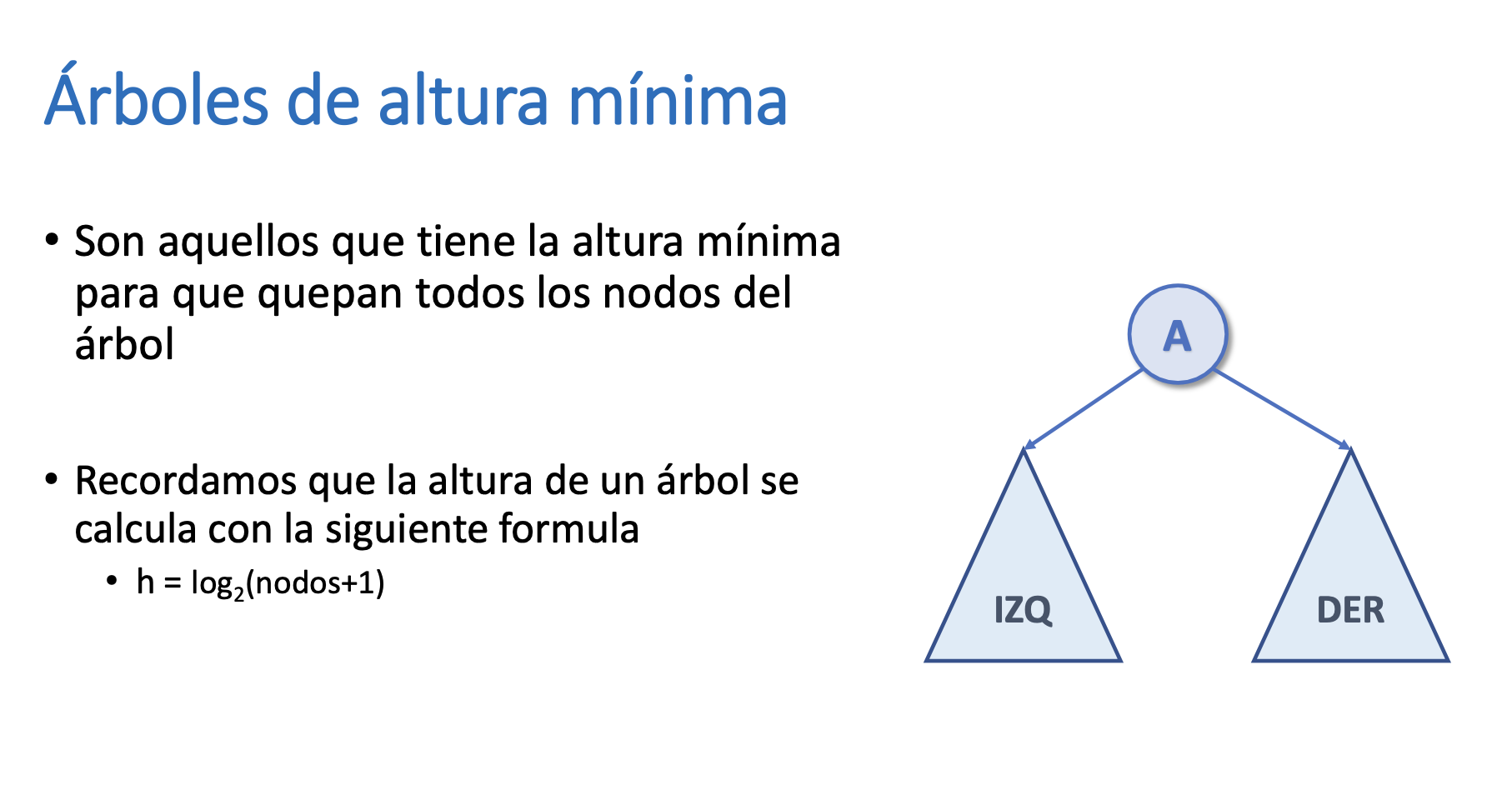
Árbol de altura mínima
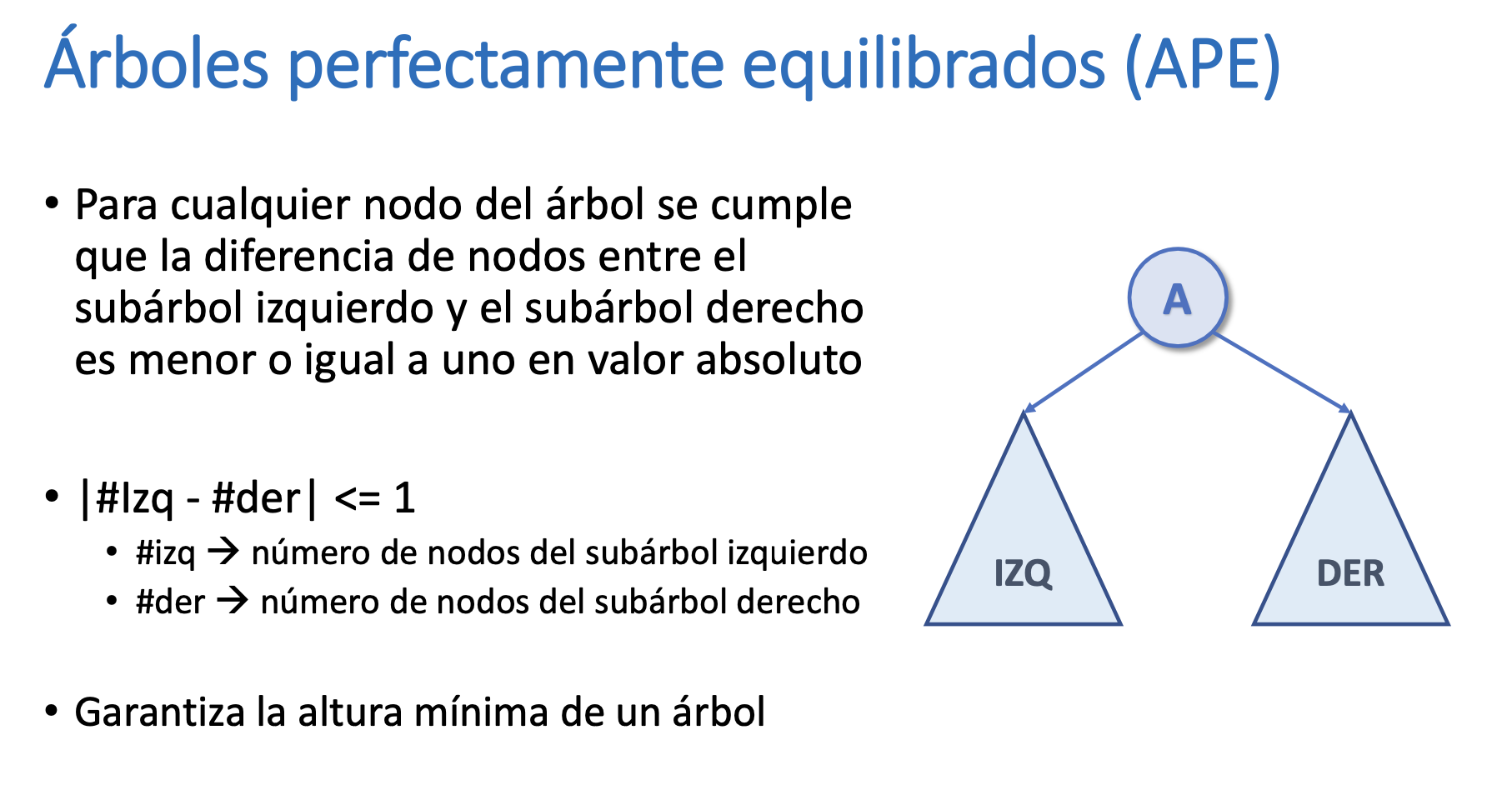
Árbol perfectamente equilibrado (APE)
Problemas de los árboles APE

Árboles AVL
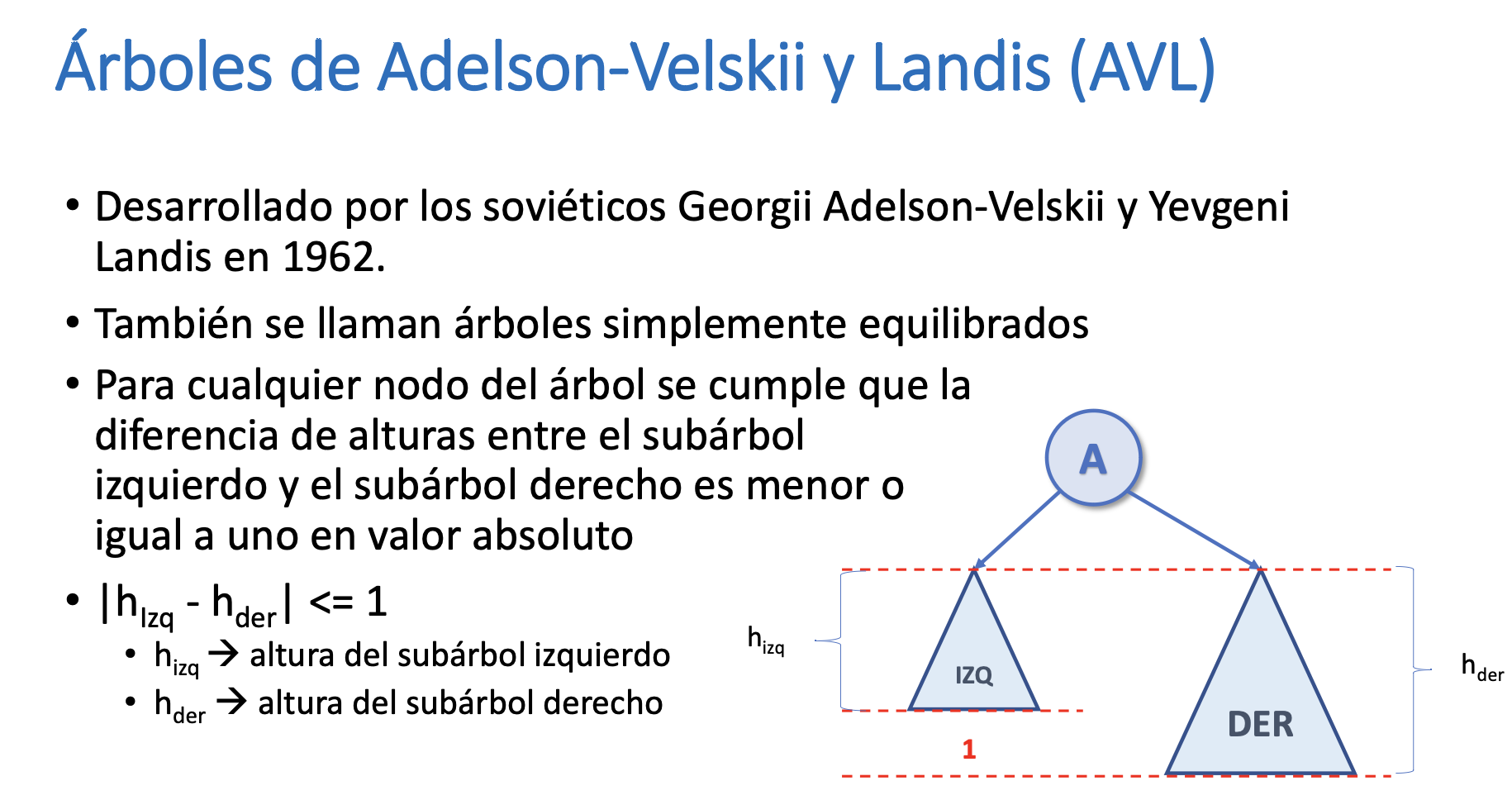
- Se habla de alturas, no de nodos como en APE
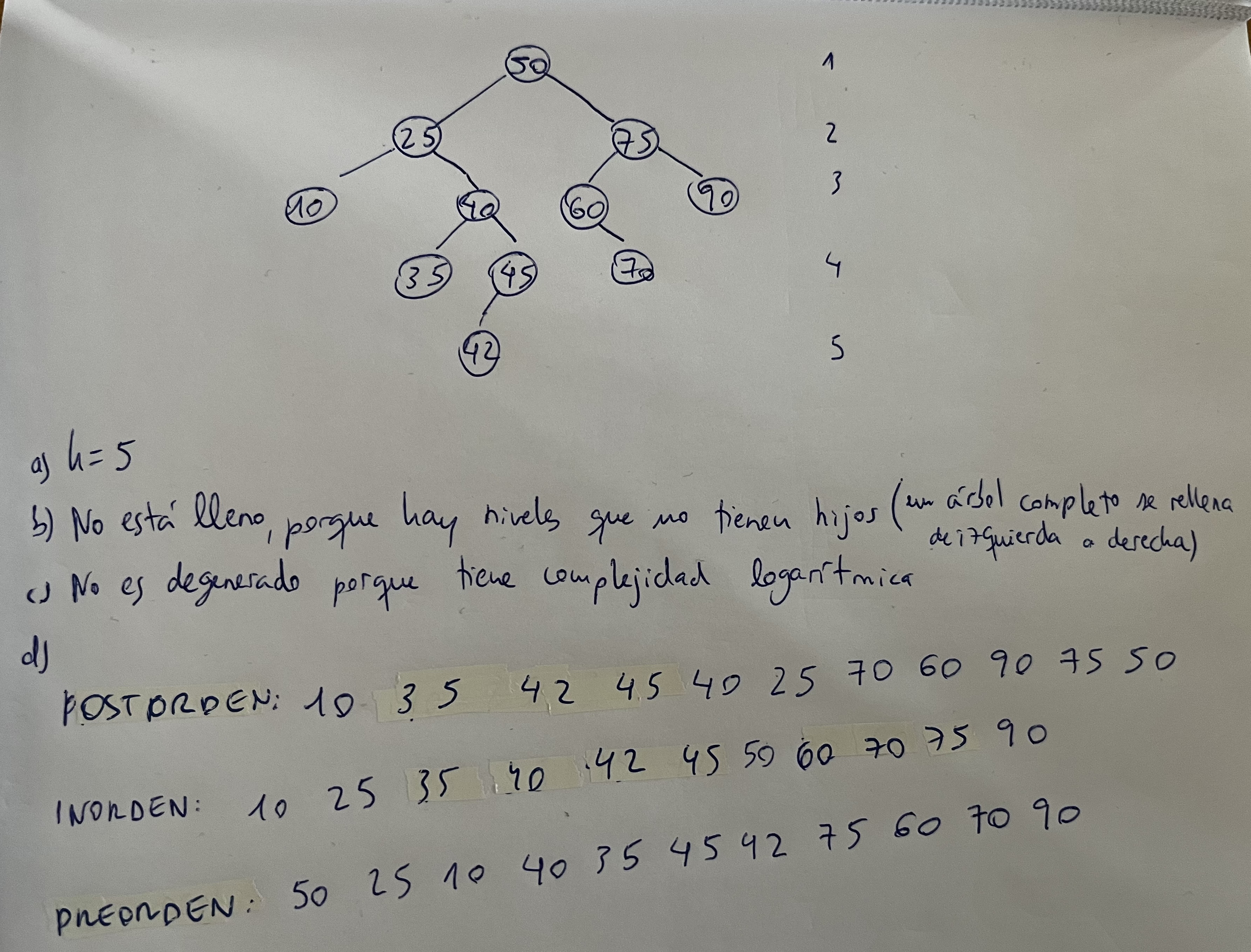
Ejercicios
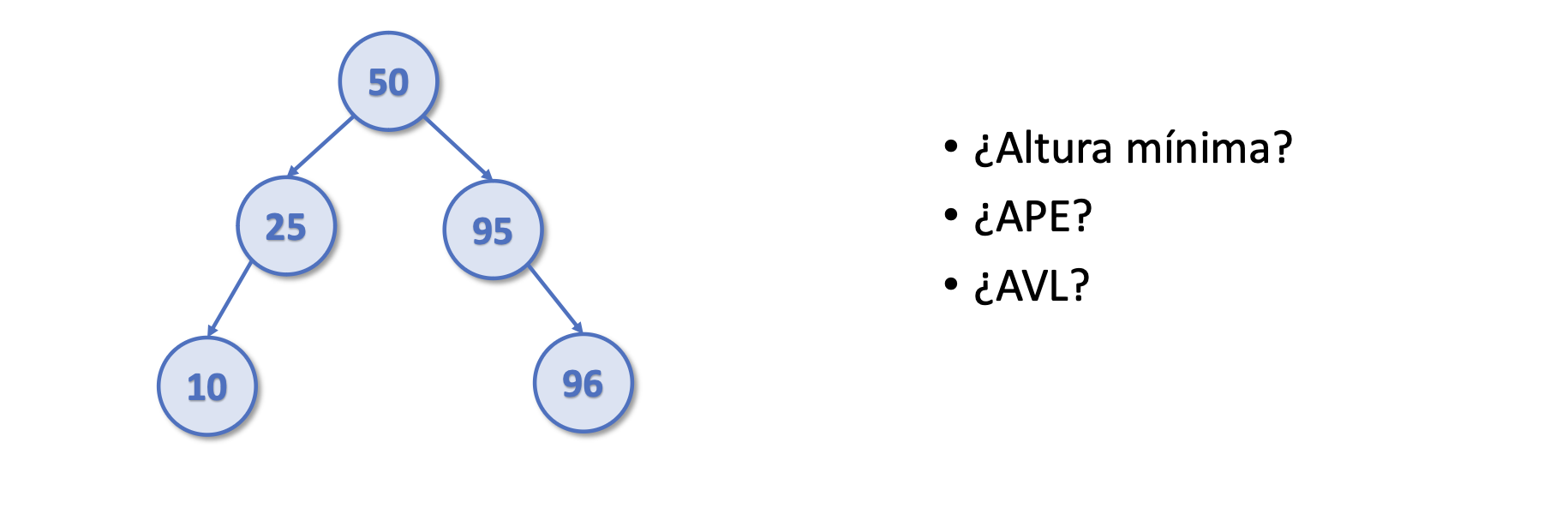
- Es de altura mínima, porque para 5 nodos necesito un árbol de 3 de altura
- También es un APE, ya que
|#Izq - #Der| <= 1 - También es AVL, ya que
|hIzq - hDer| <= 1
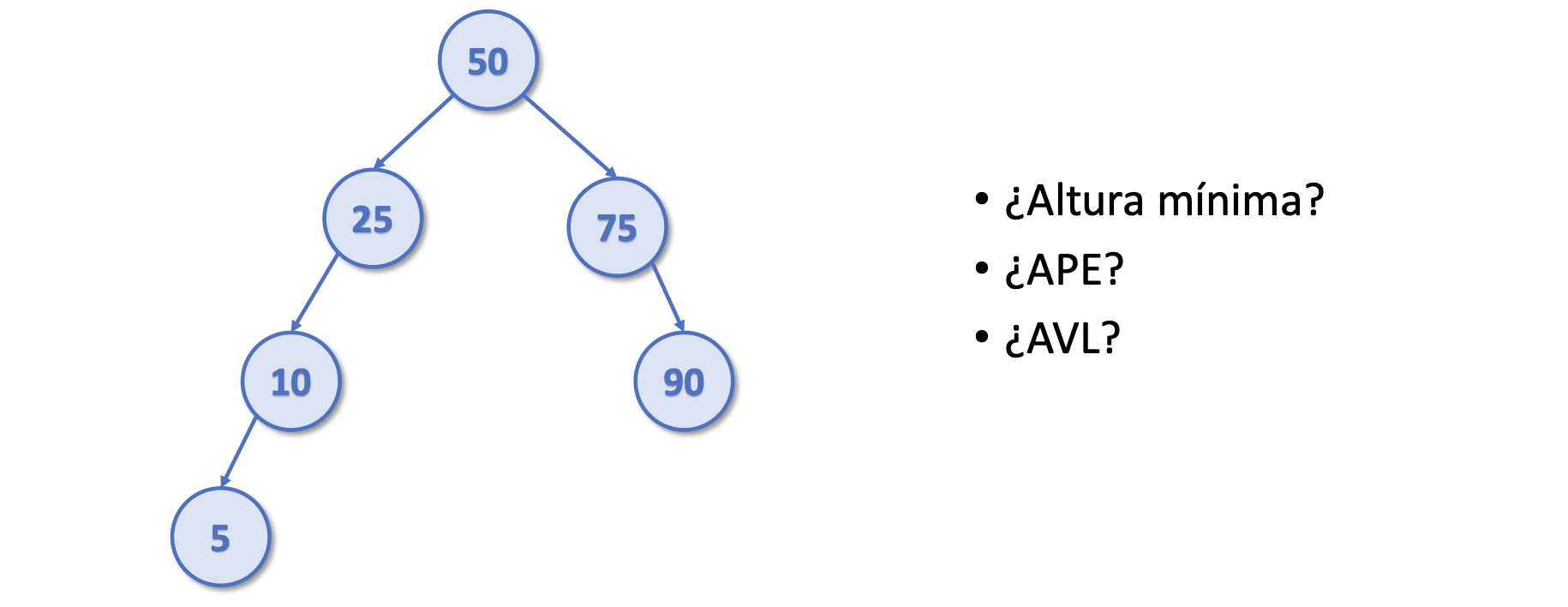
- No es de altura mínima, porque para 6 nodos necesito un árbol de 3 de altura
- No es un APE, ya que no se cumple
|#Izq - #Der| <= 1para el 25 - No es AVL, ya que no se cumple
|hIzq - hDer| <= 1para el 25

- Es de altura mínima, porque para 5 nodos necesito un árbol de 3 de altura
- No es un APE, ya que no se cumple
|#Izq - #Der| <= 1para 50 - Es AVL, ya que
|hIzq - hDer| <= 1
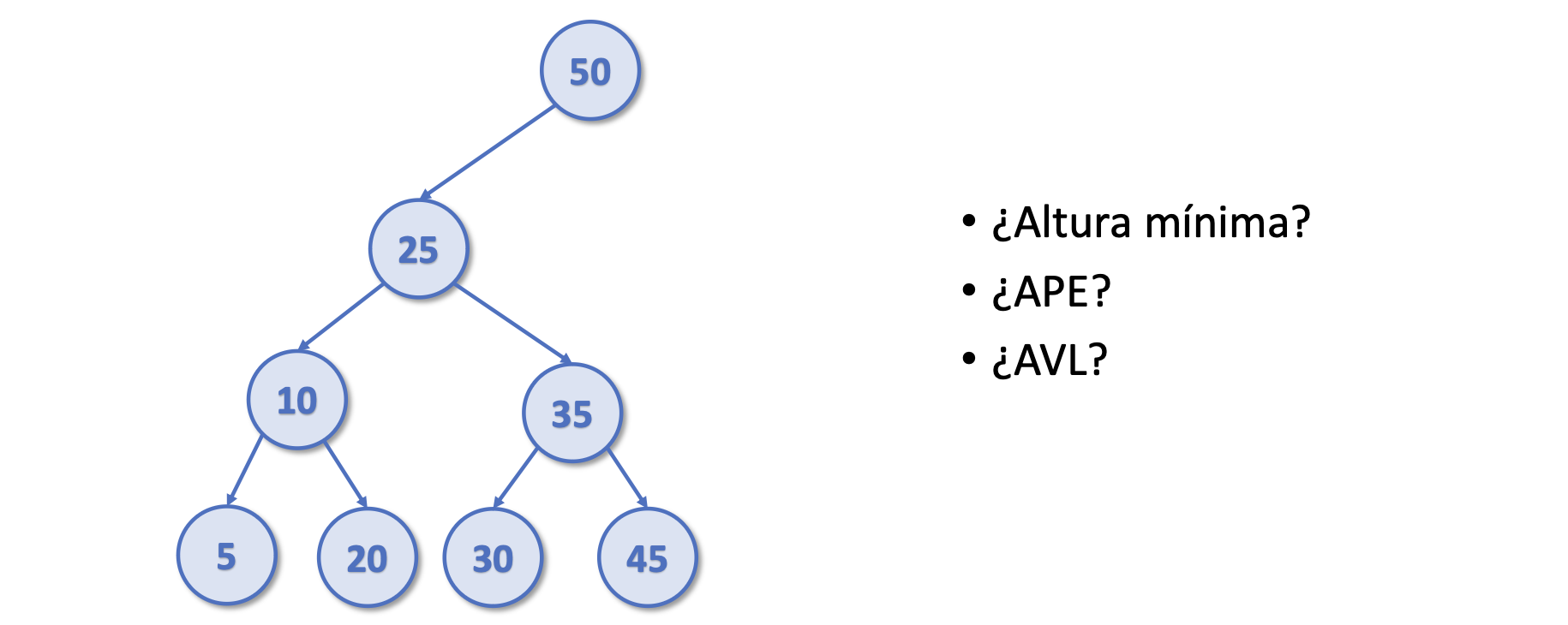
- Si es de altura mínima, porque para 8 nodos necesito un árbol de 3 de altura
- No es un APE, ya que no se cumple
|#Izq - #Der| <= 1para el 25 - No es AVL, ya que no se cumple
|hIzq - hDer| <= 1para el 25
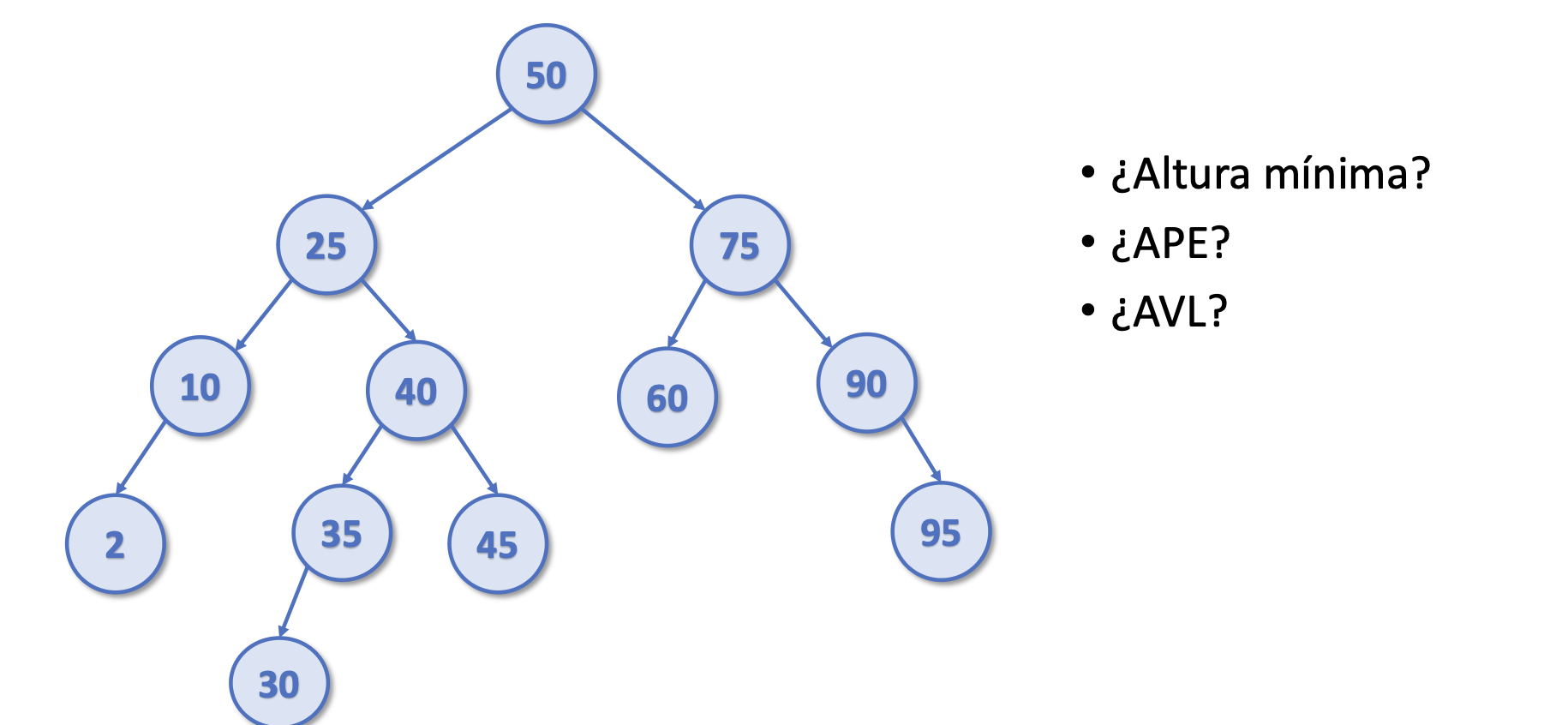
- No es de altura mínima, porque para 8 nodos necesito un árbol de 3 de altura
- No es un APE, ya que no se cumple
|#Izq - #Der| <= 1para el 25 - No es AVL, ya que no se cumple
|hIzq - hDer| <= 1para el 25
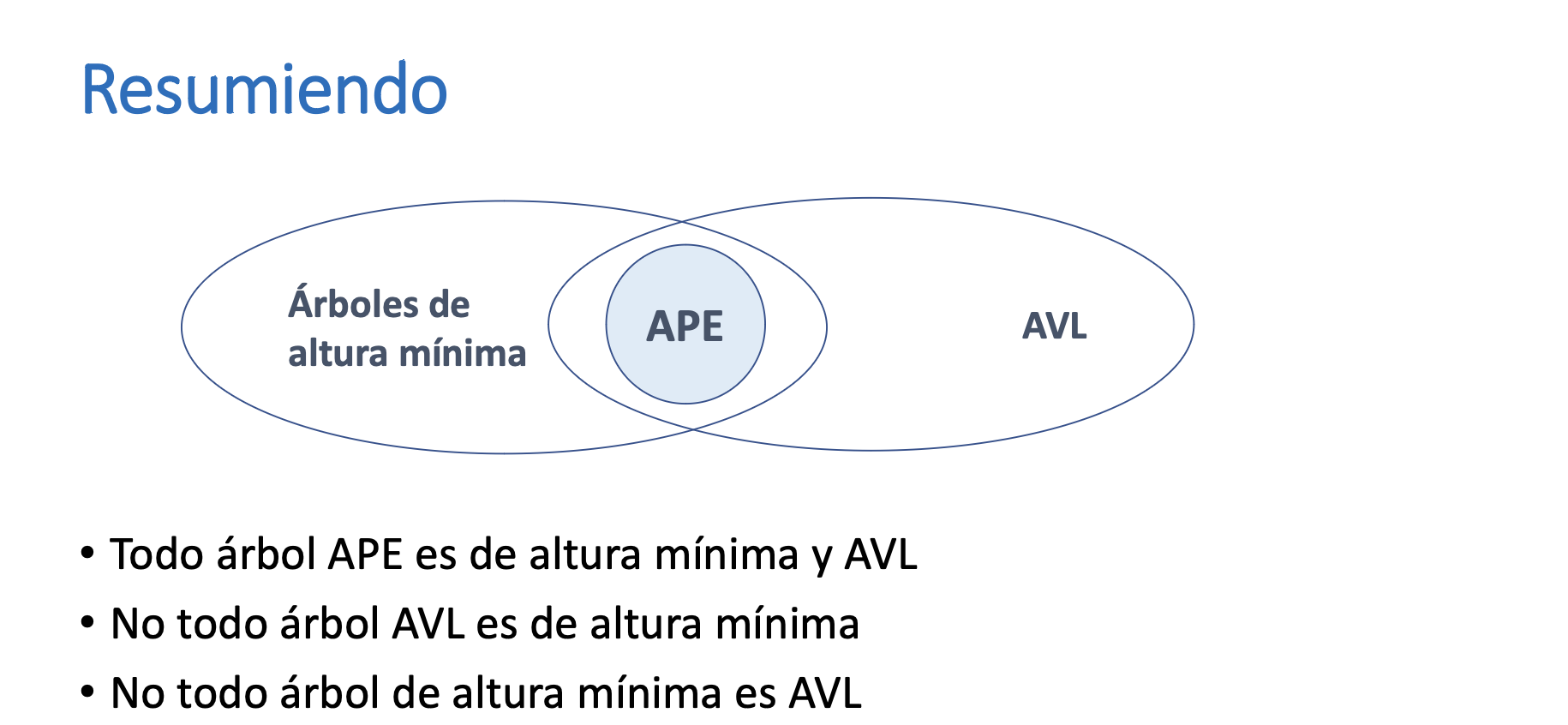
Resumen Ahmin, APE, AVL
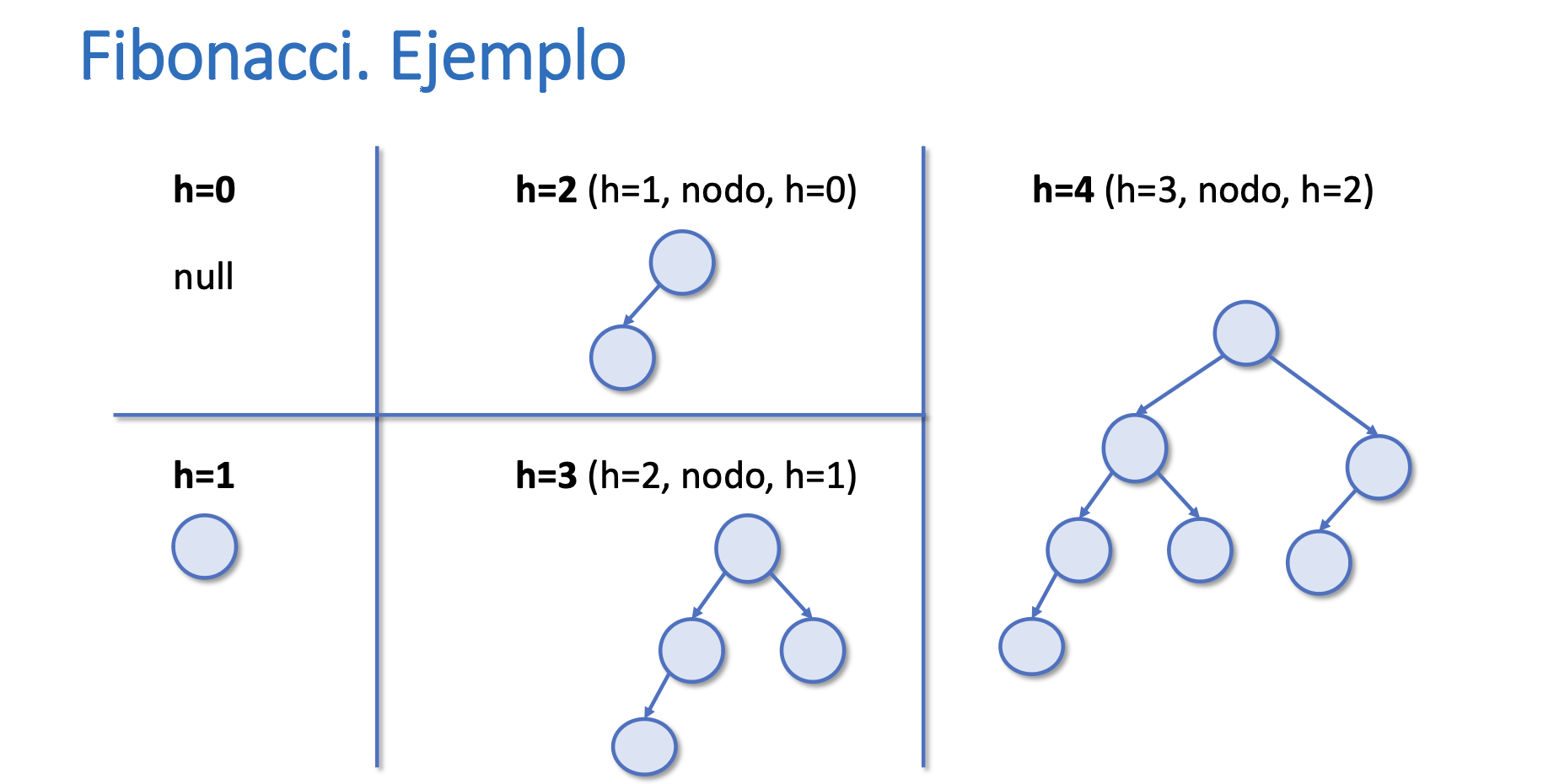
Árboles de Fibonacci

Ejemplo
Resultados

Implementación de un AVL
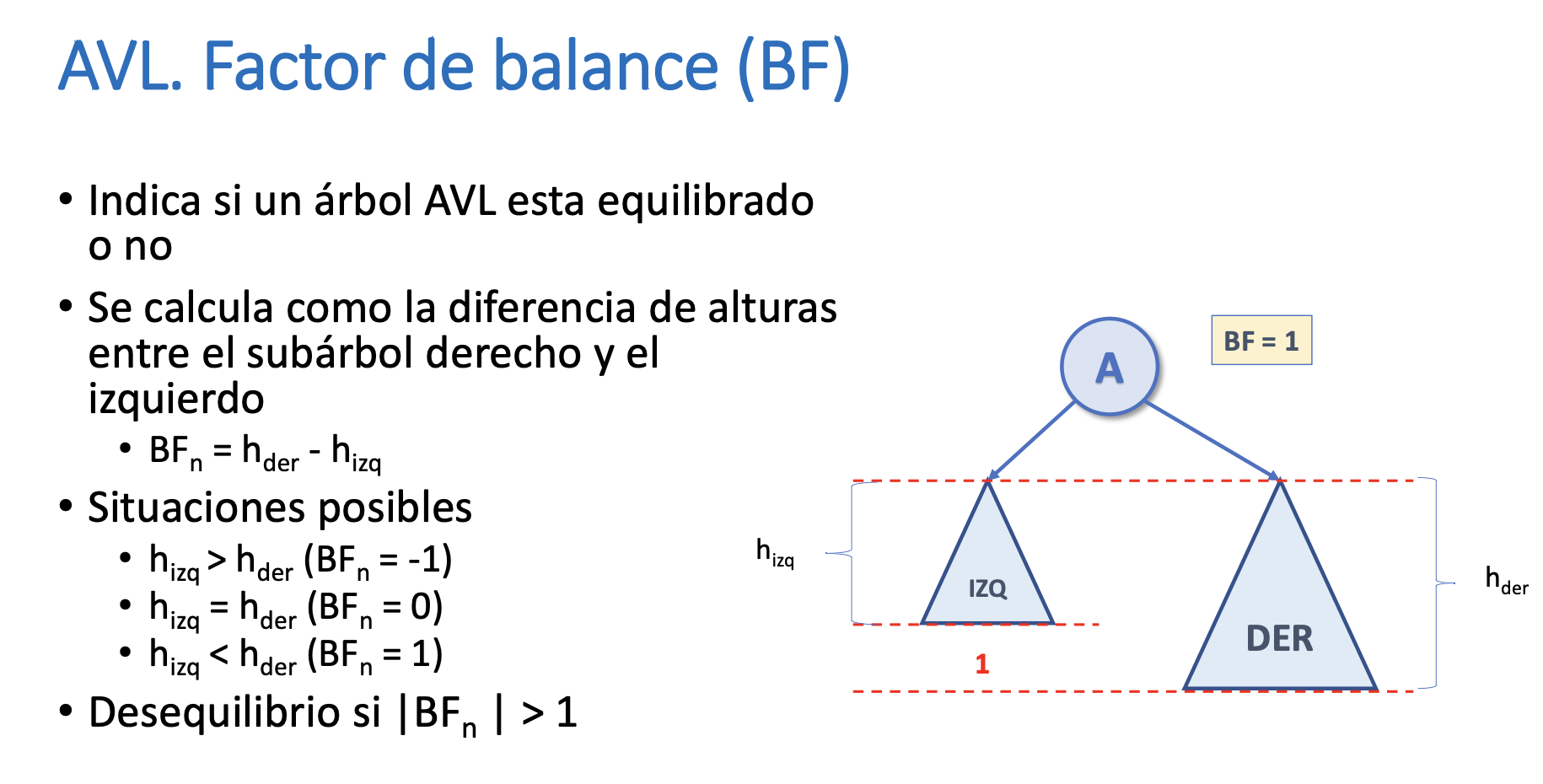
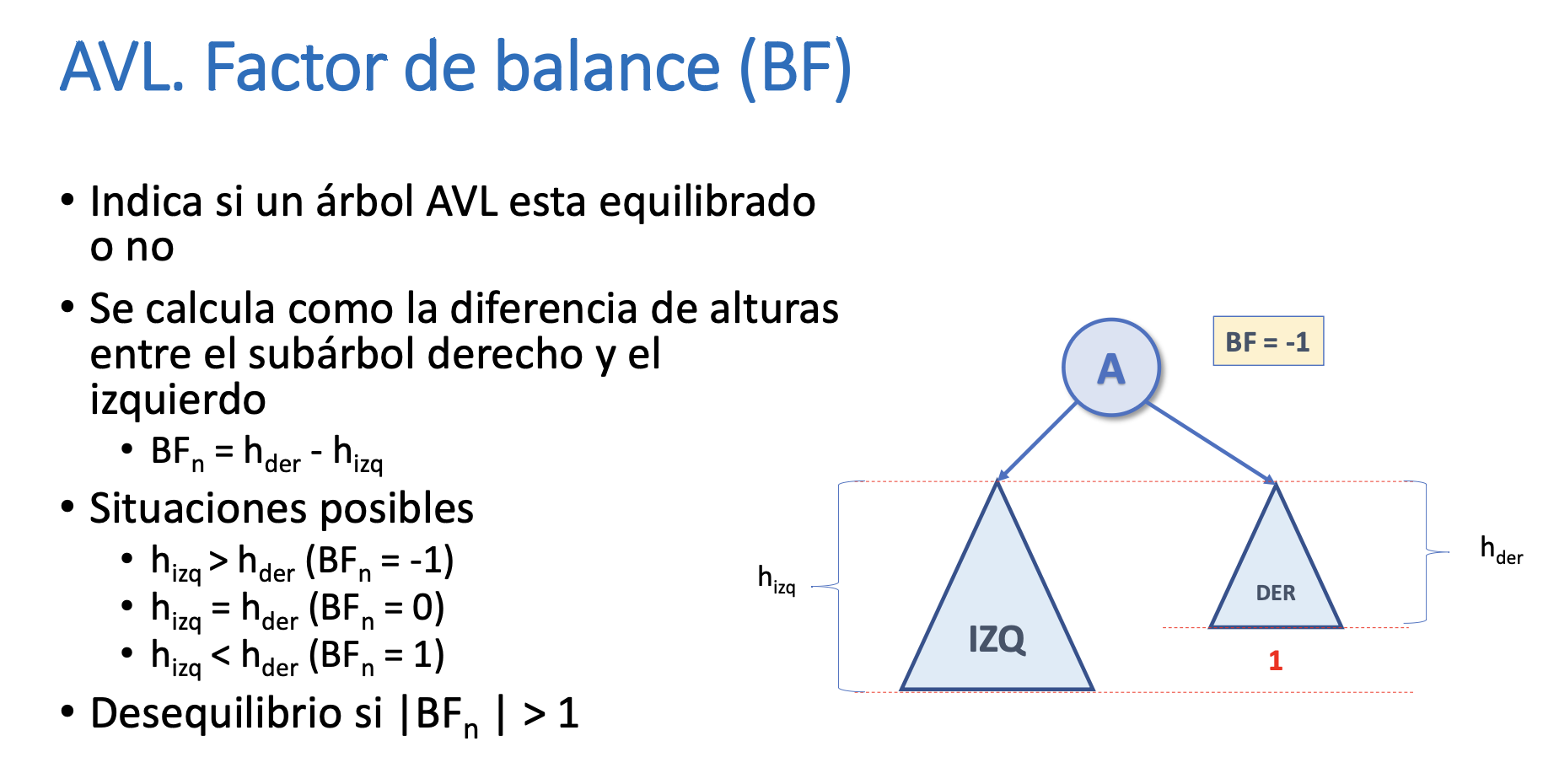
Factor de Balance (BF)
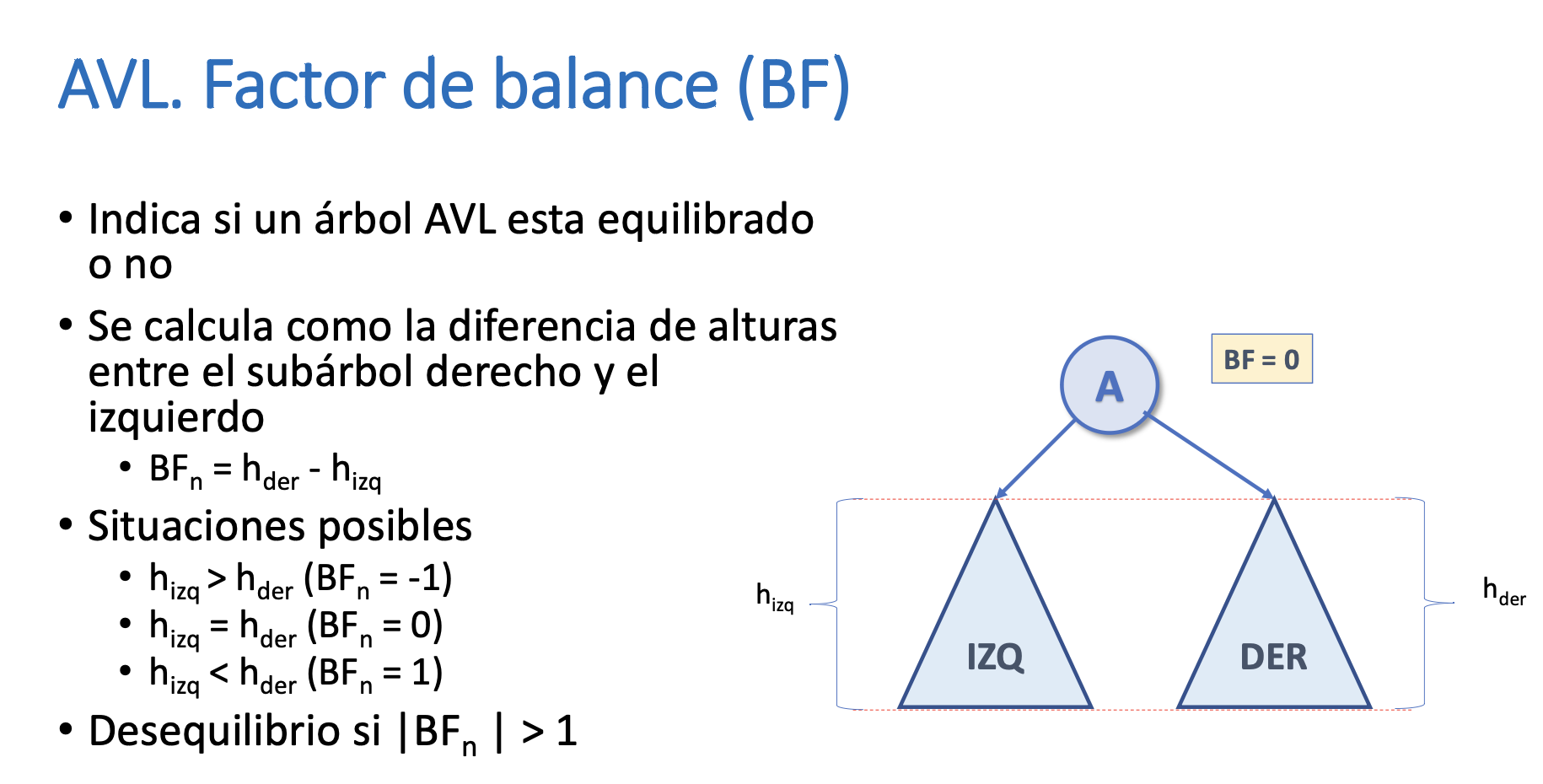
AVL. Añadir una clave a un árbol


Rotación Simple Derecha
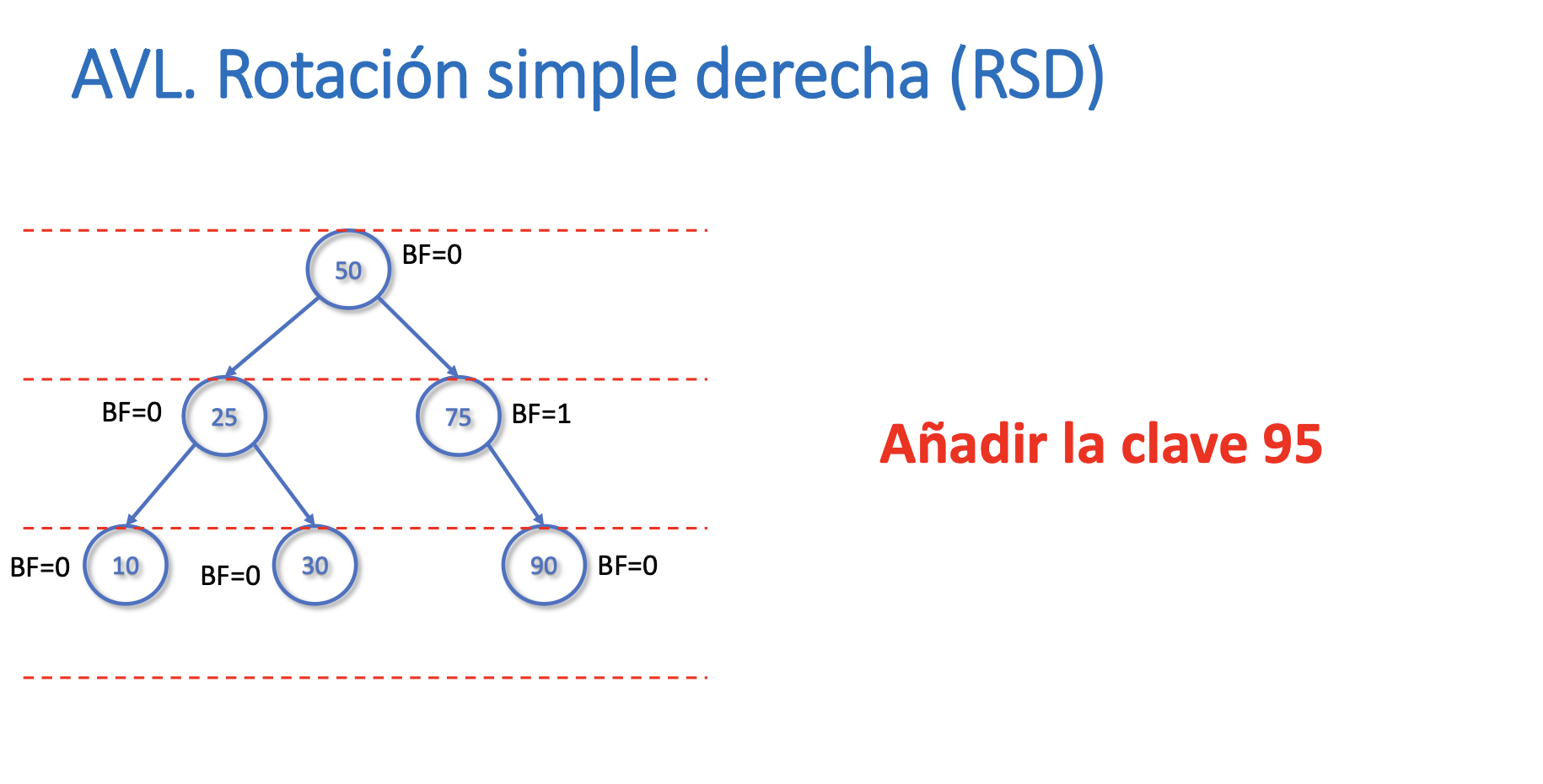
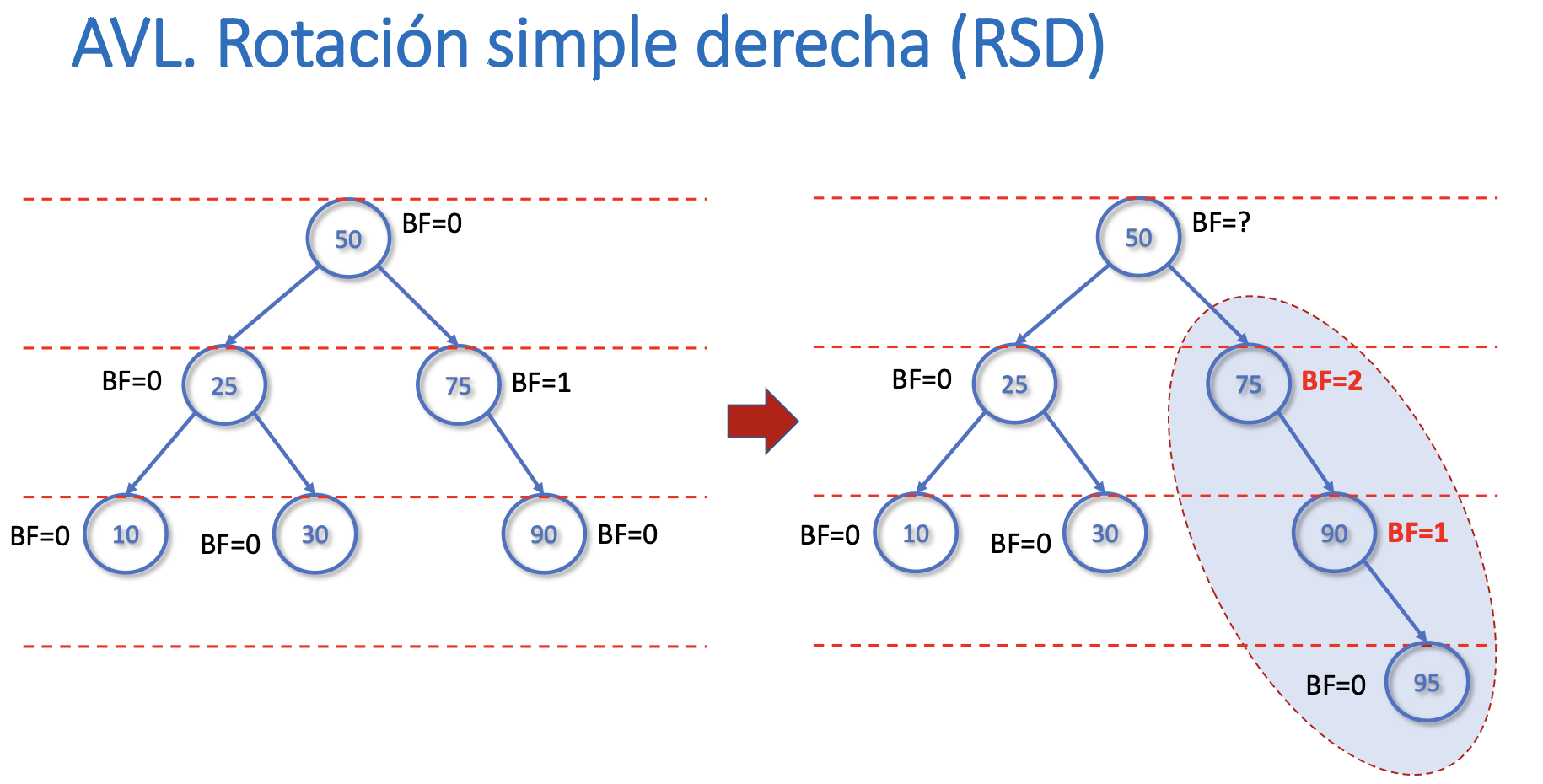
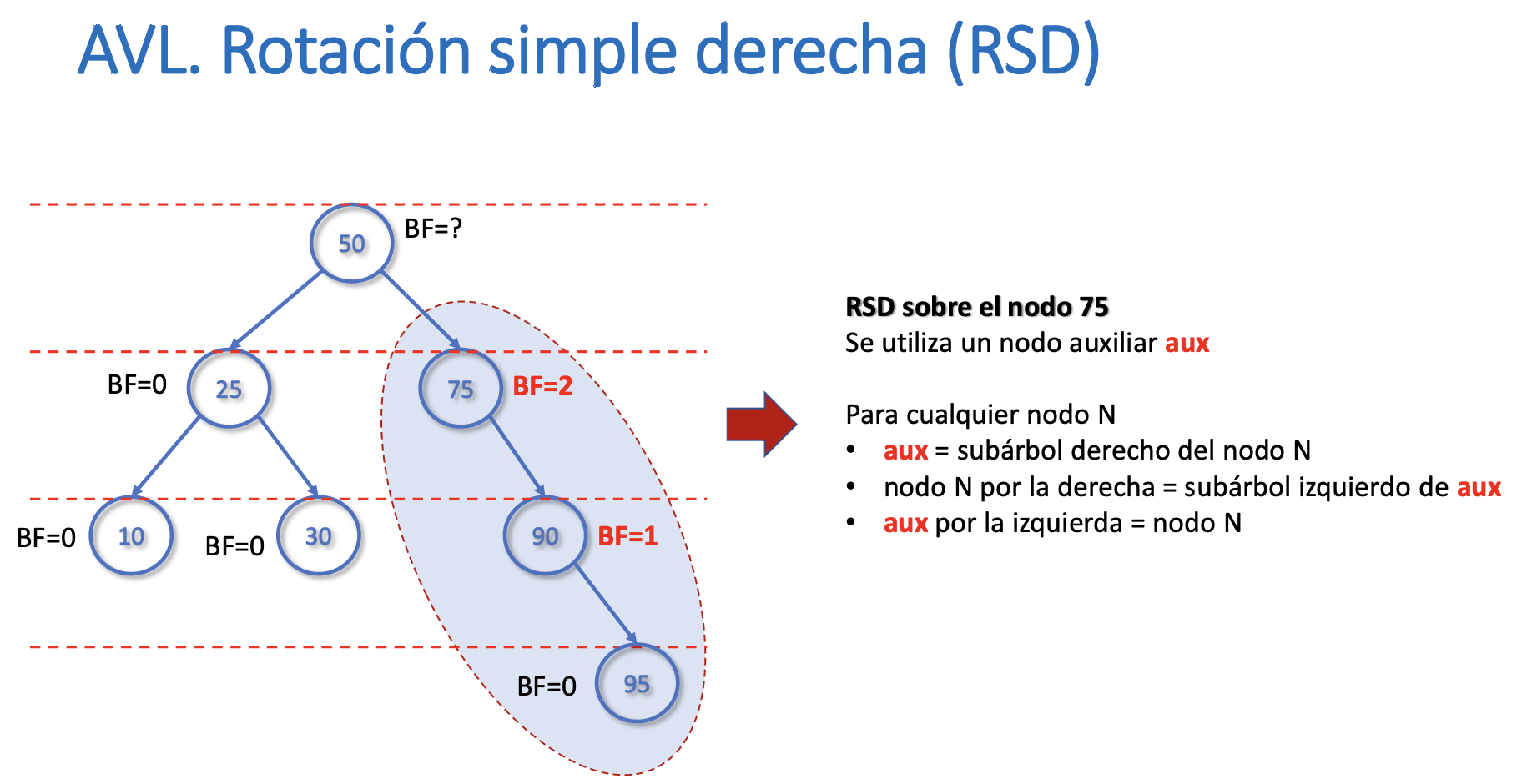
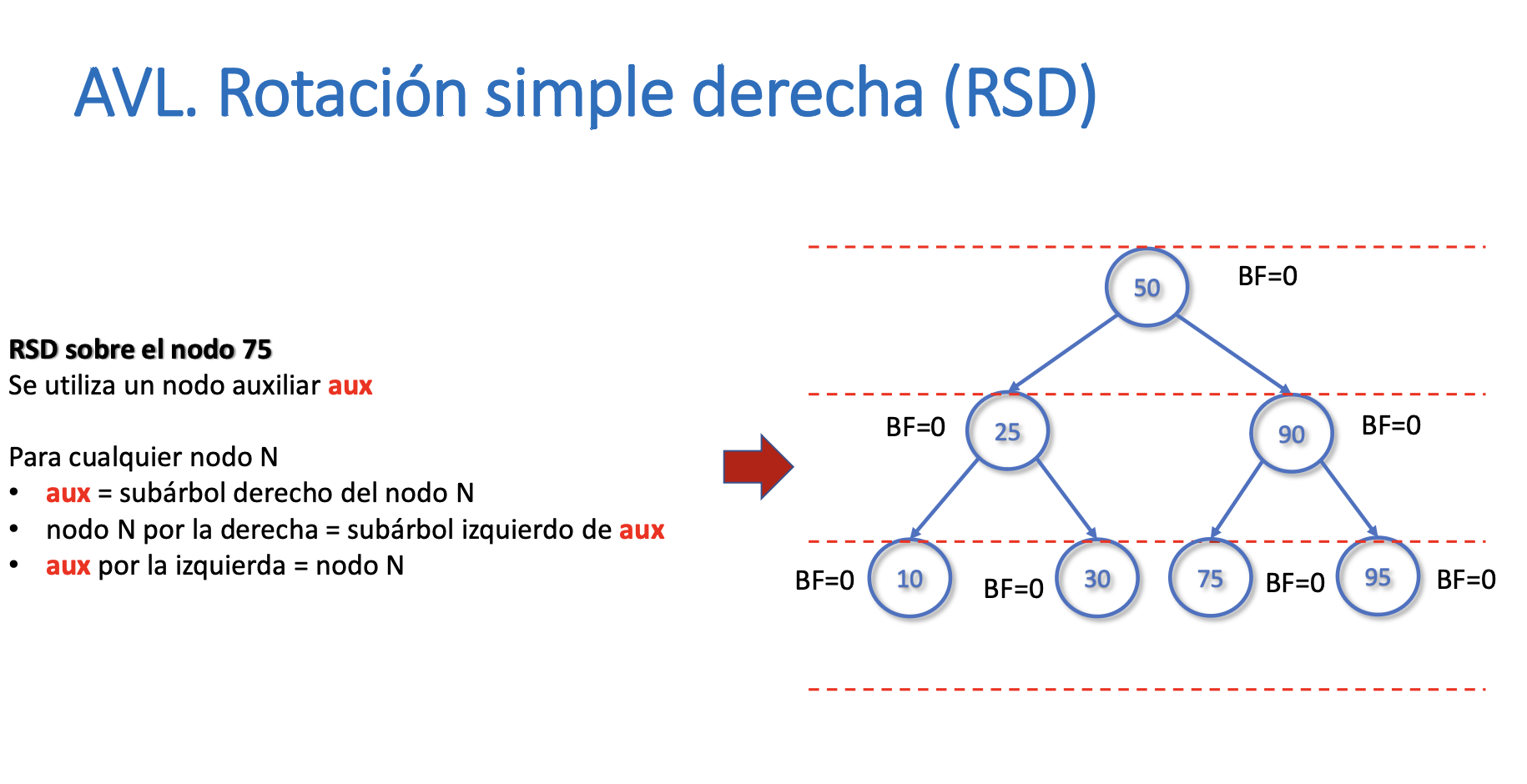
Rotación simple izquierda (RSI)
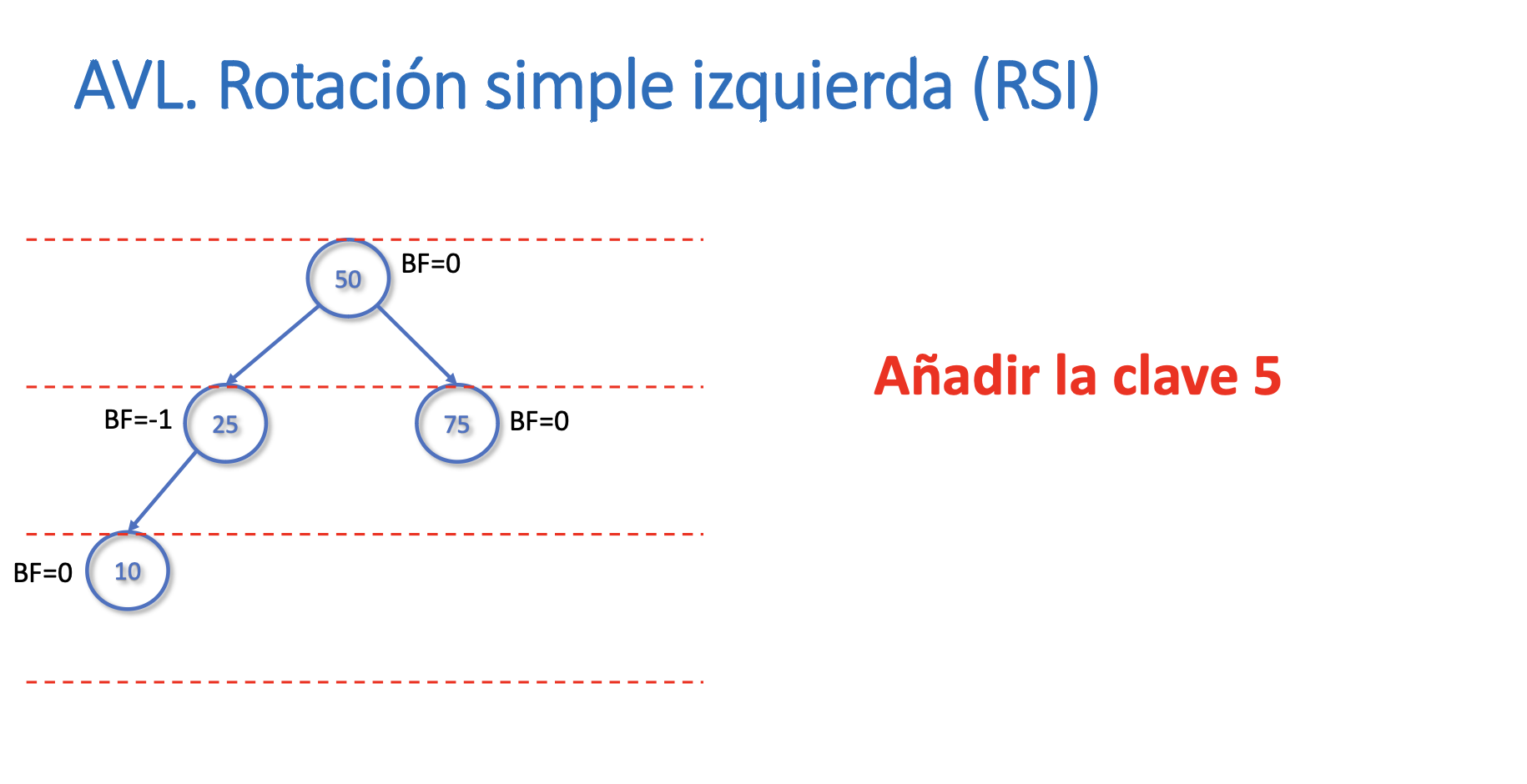
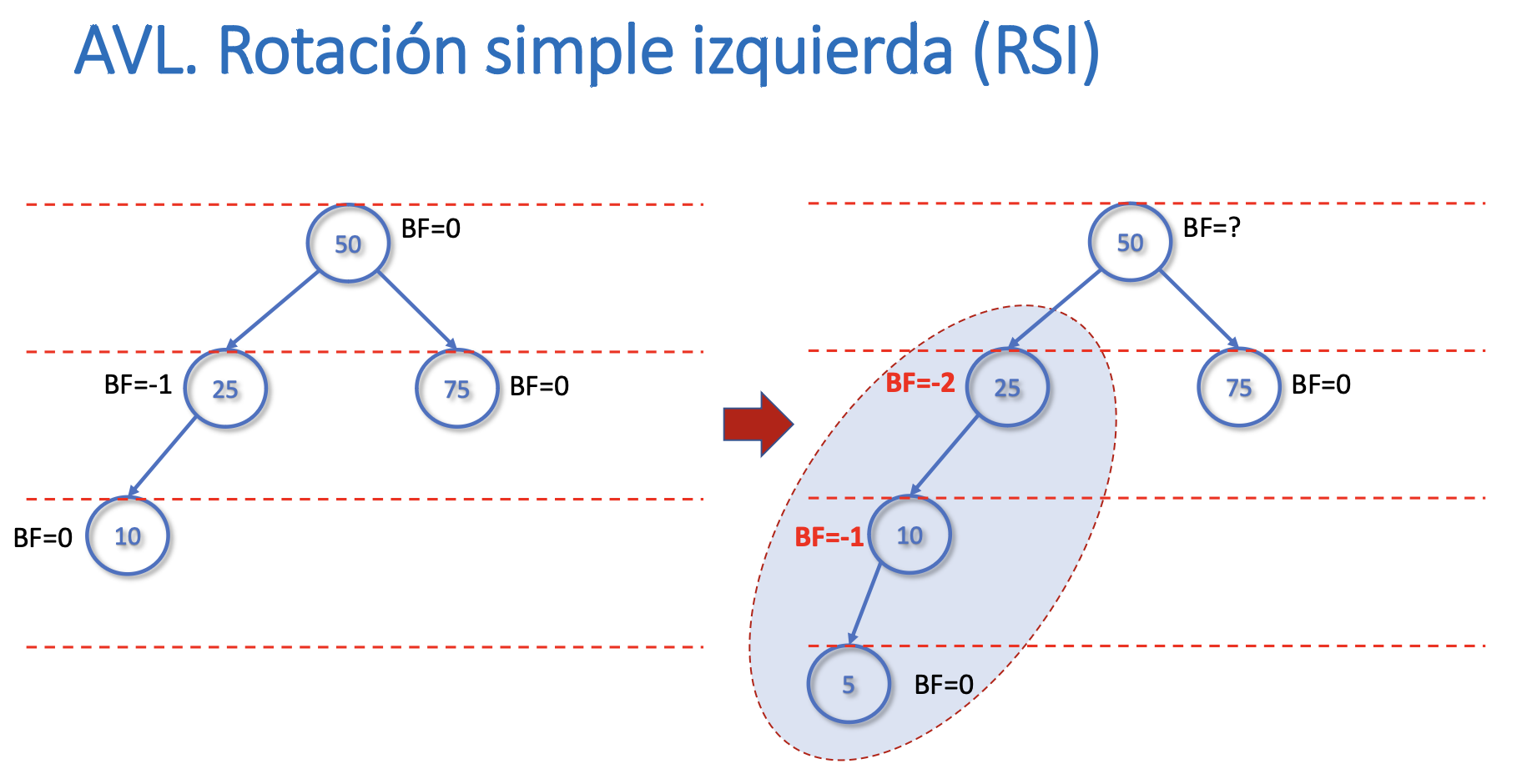
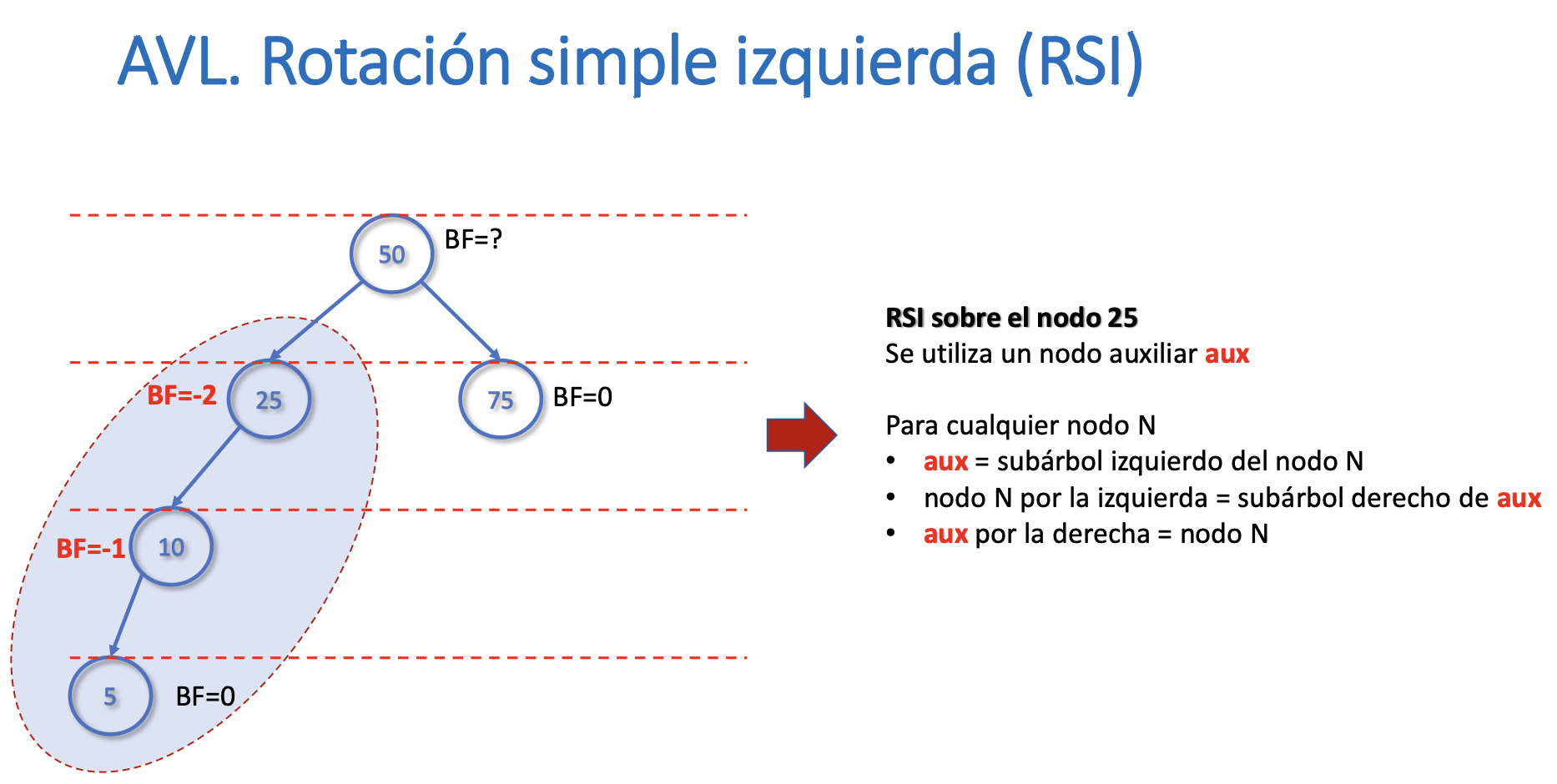
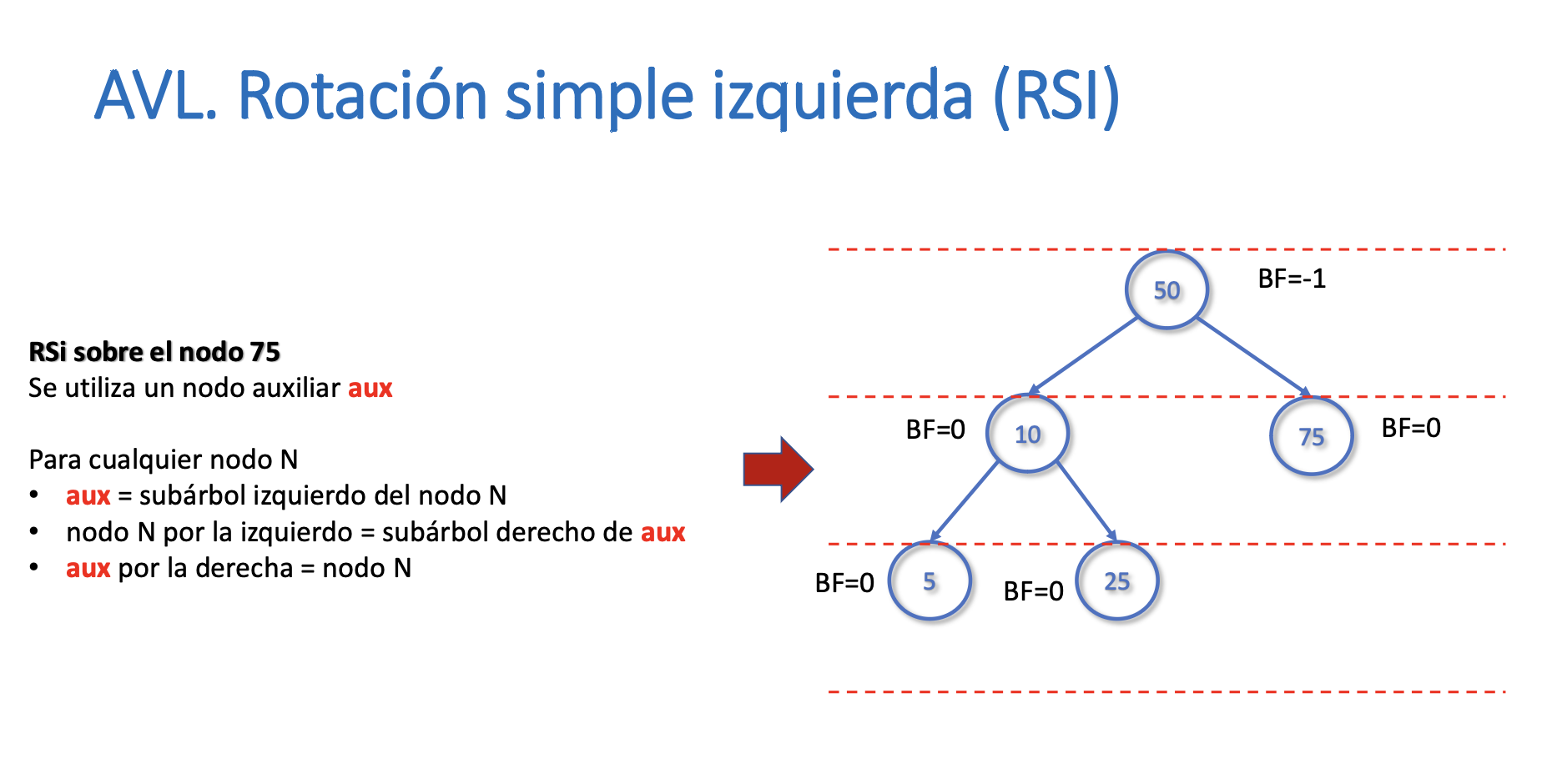
- Tiene complejidad O(1)
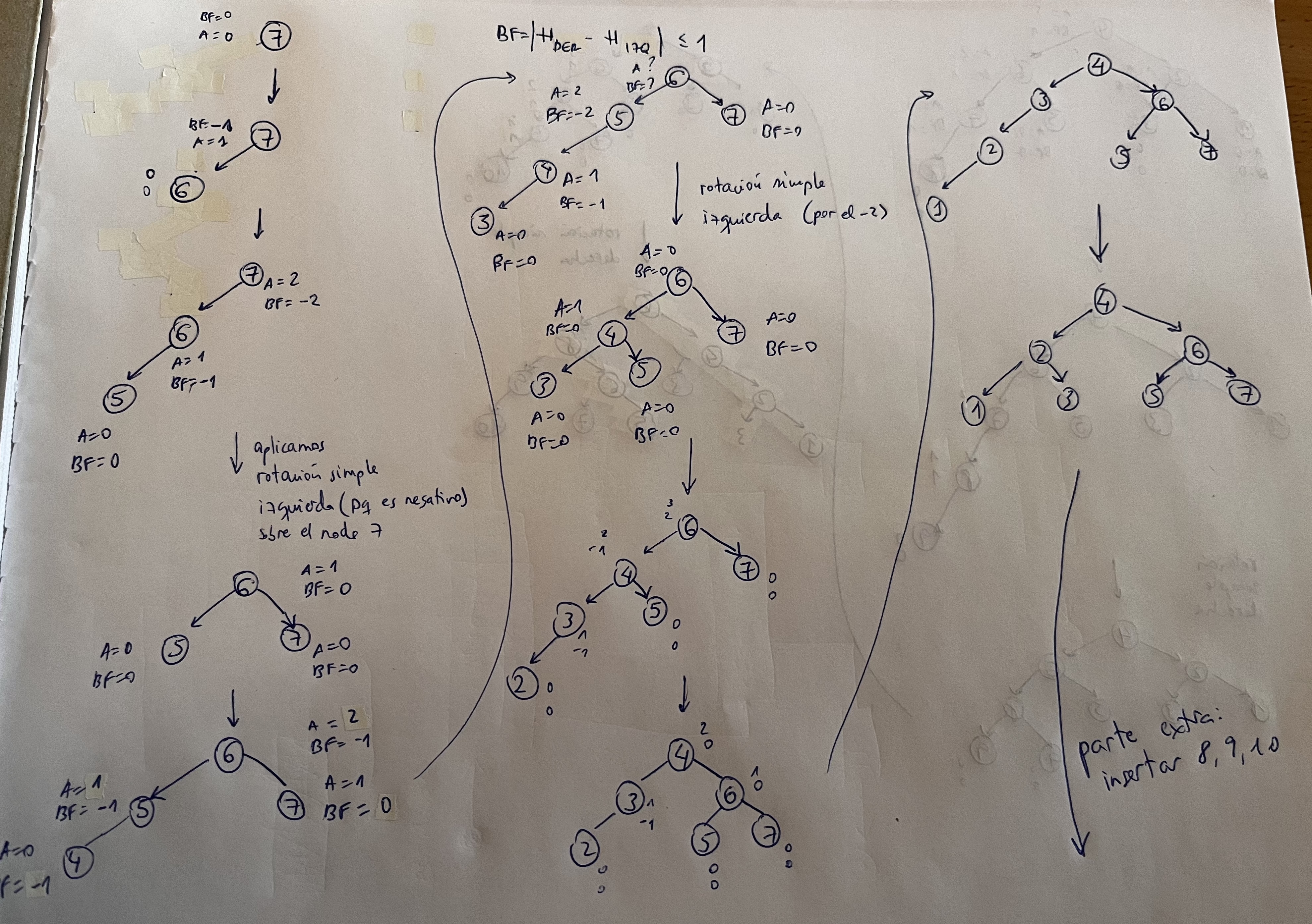
Ejercicios Rotación simple

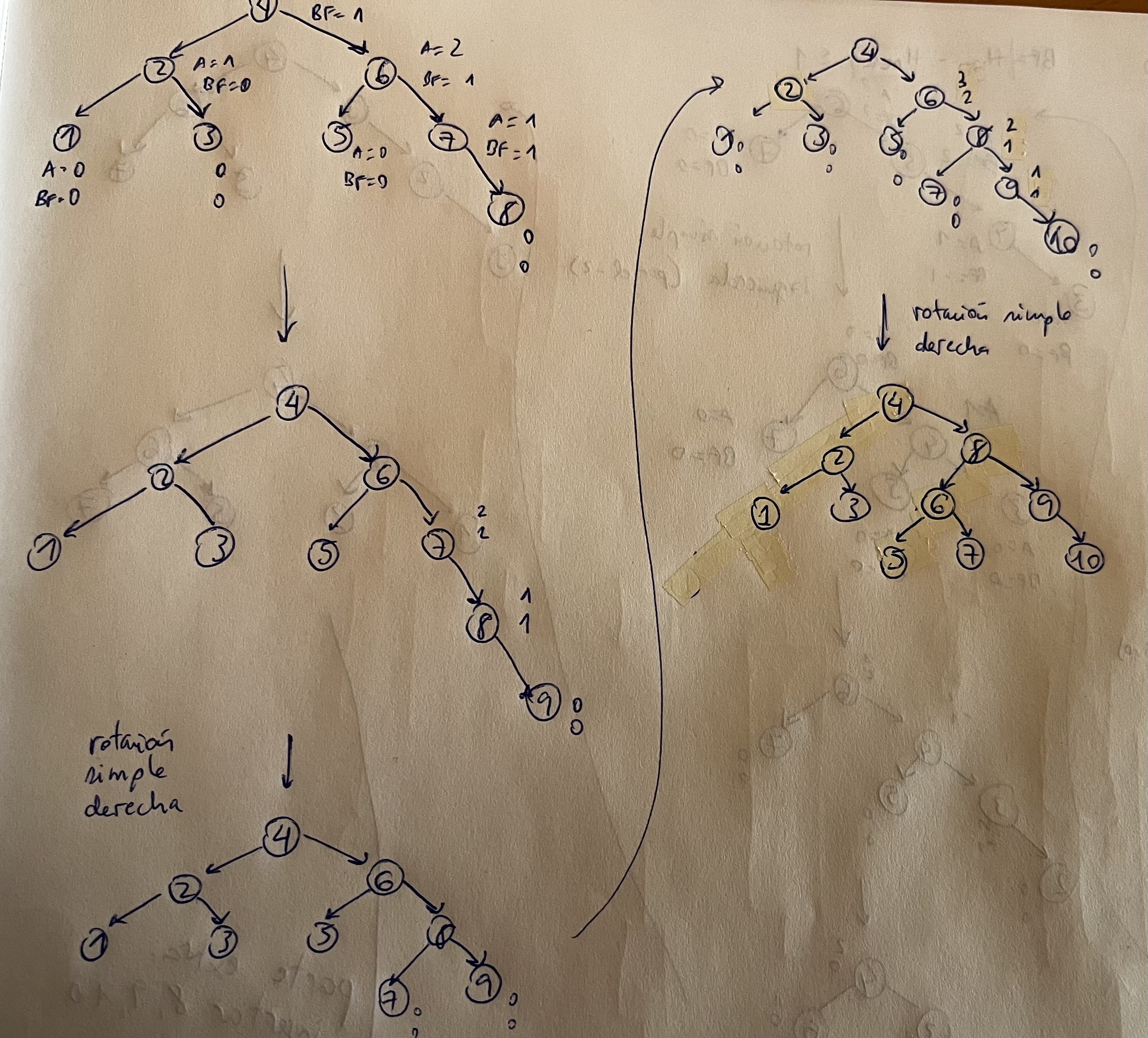
La complejidad de insertar los nodos (salvo el raíz que es O(1)) es Olog(n)
Rotación doble derecha (RDD)
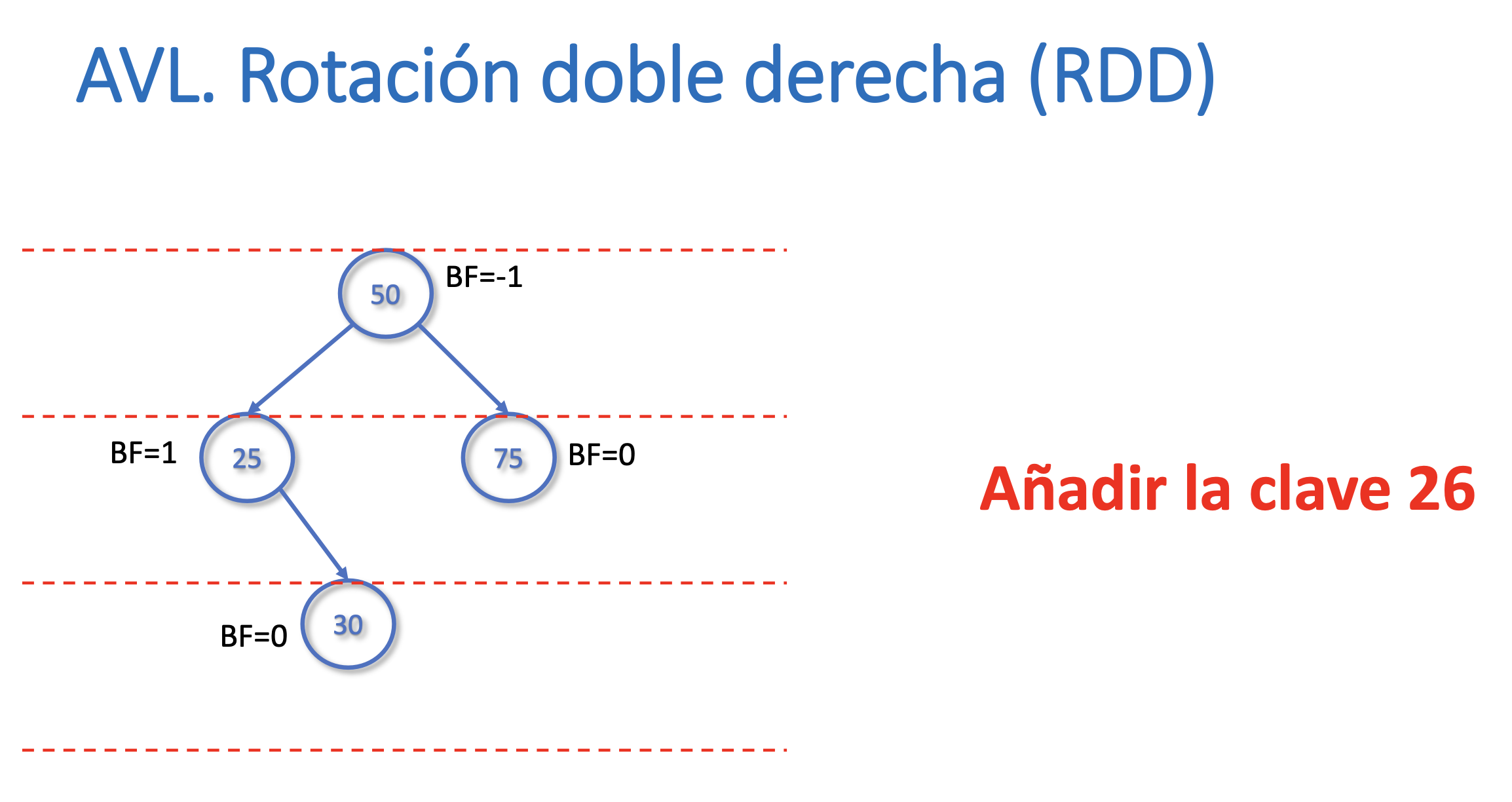
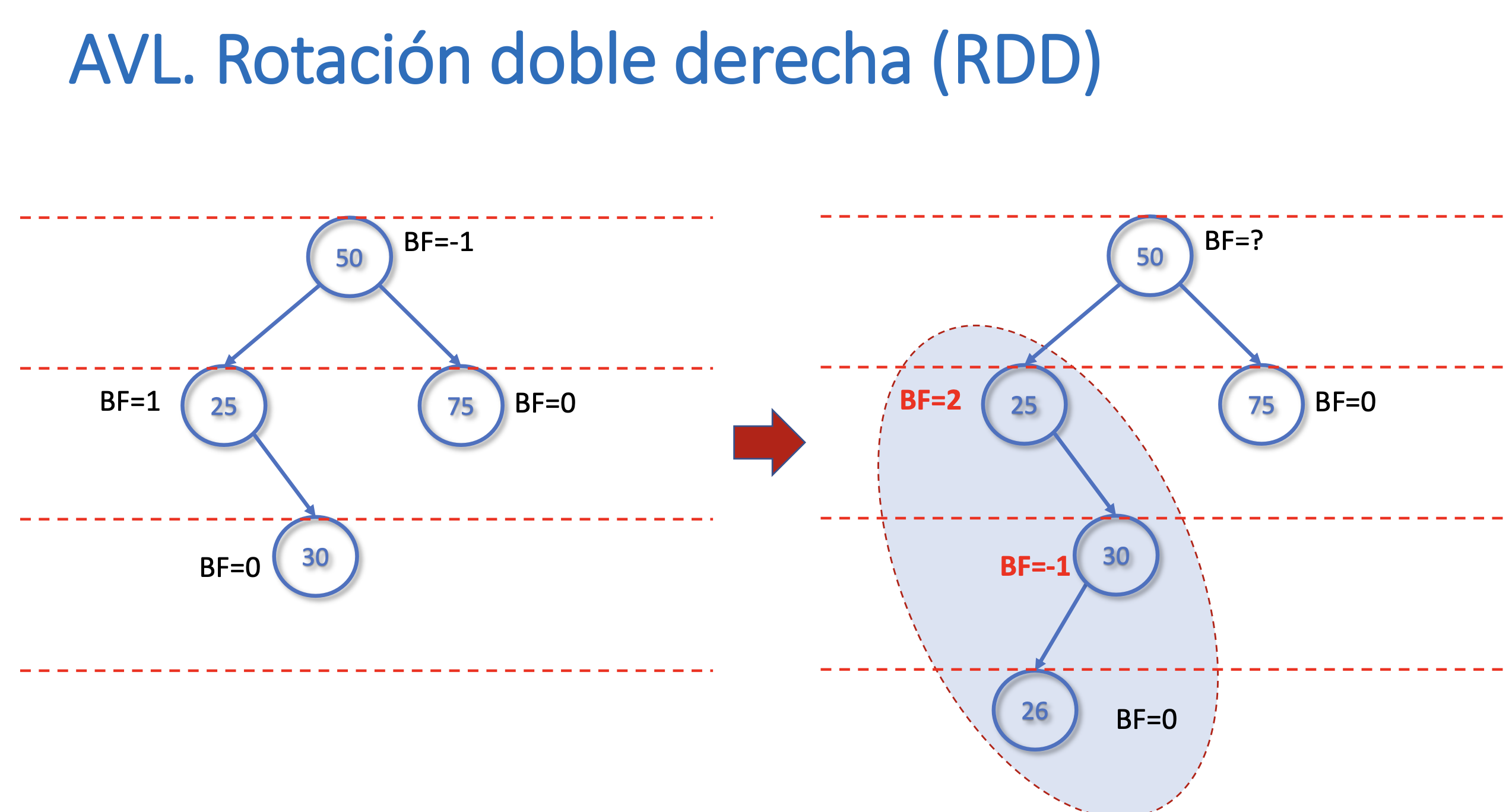
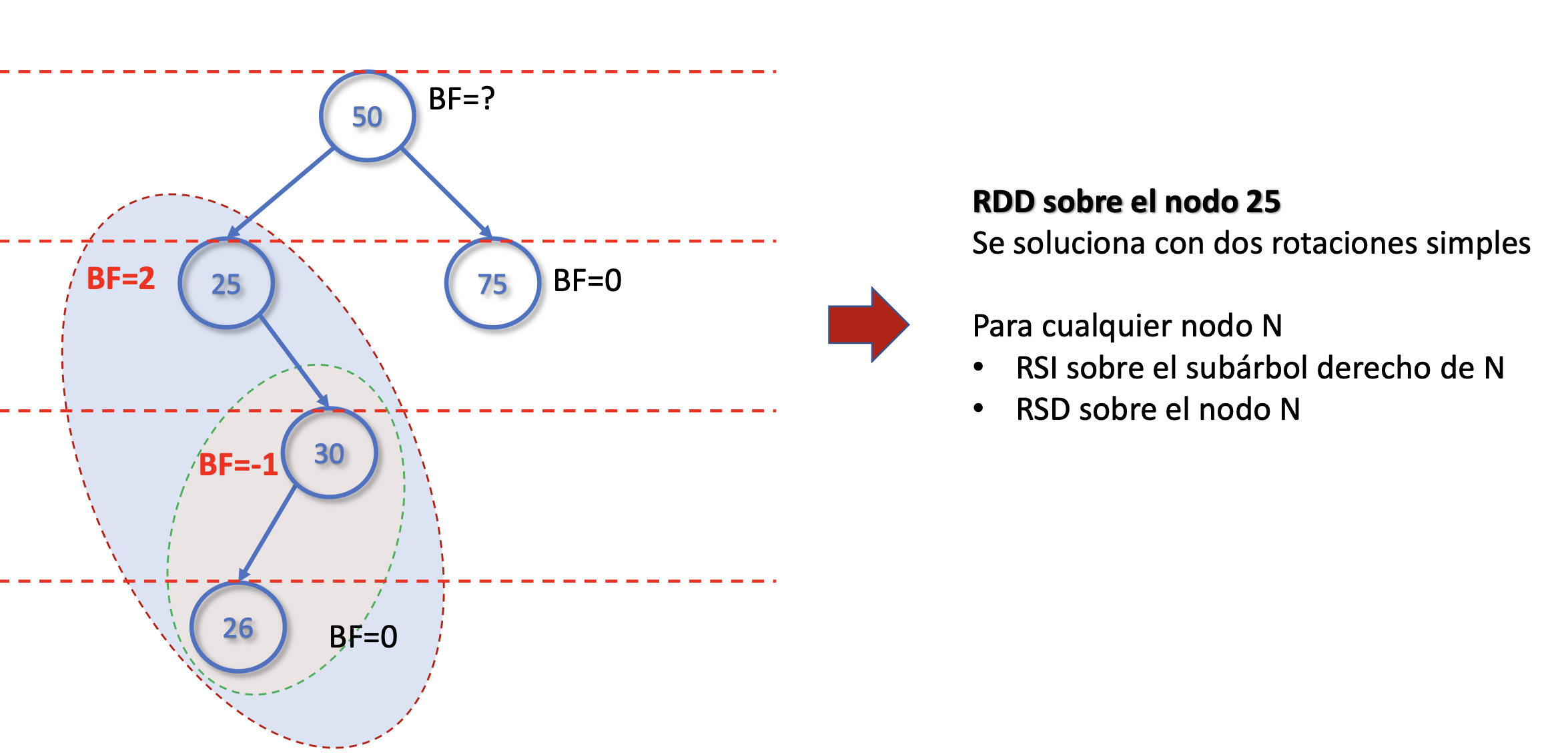
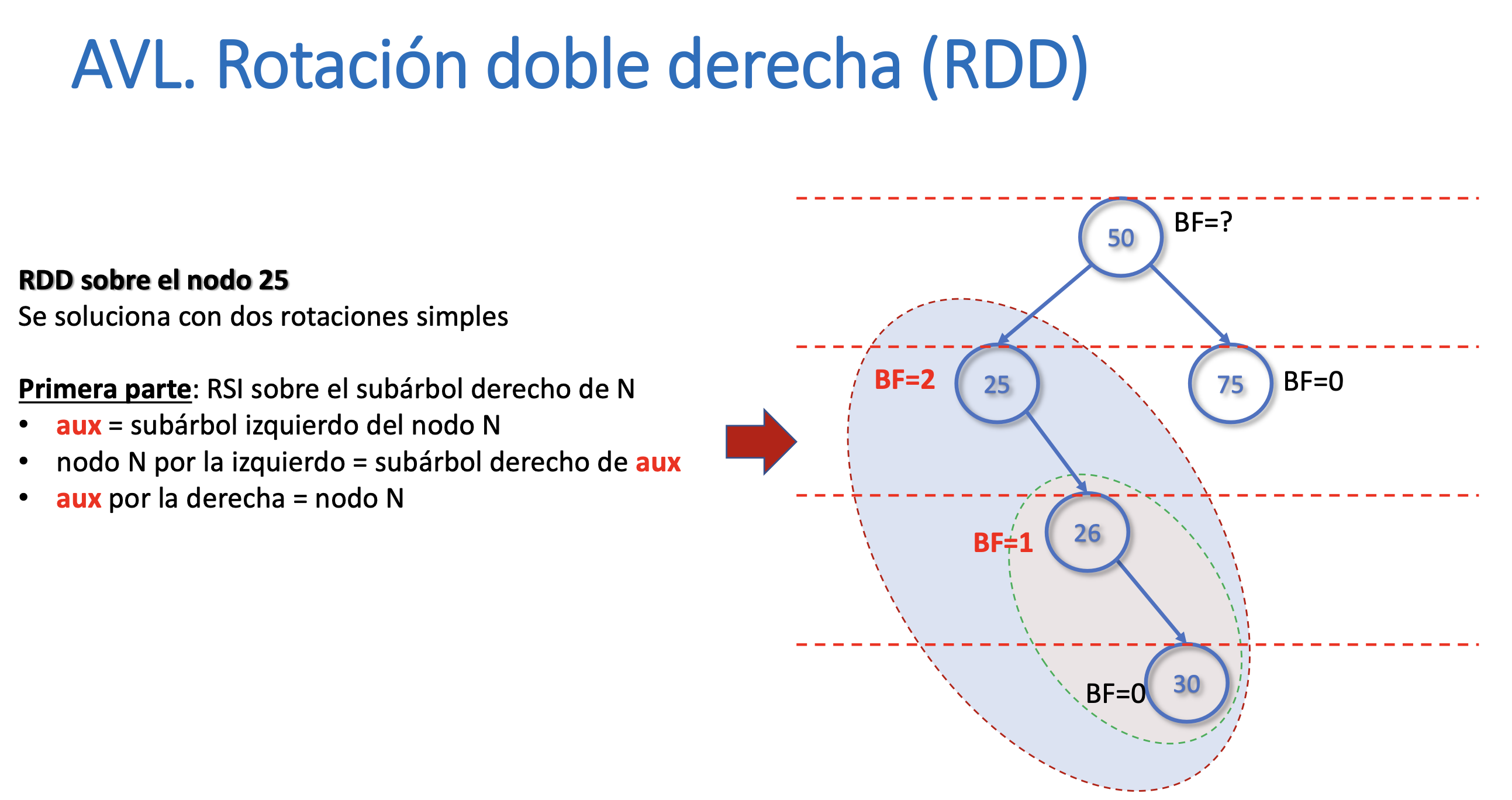
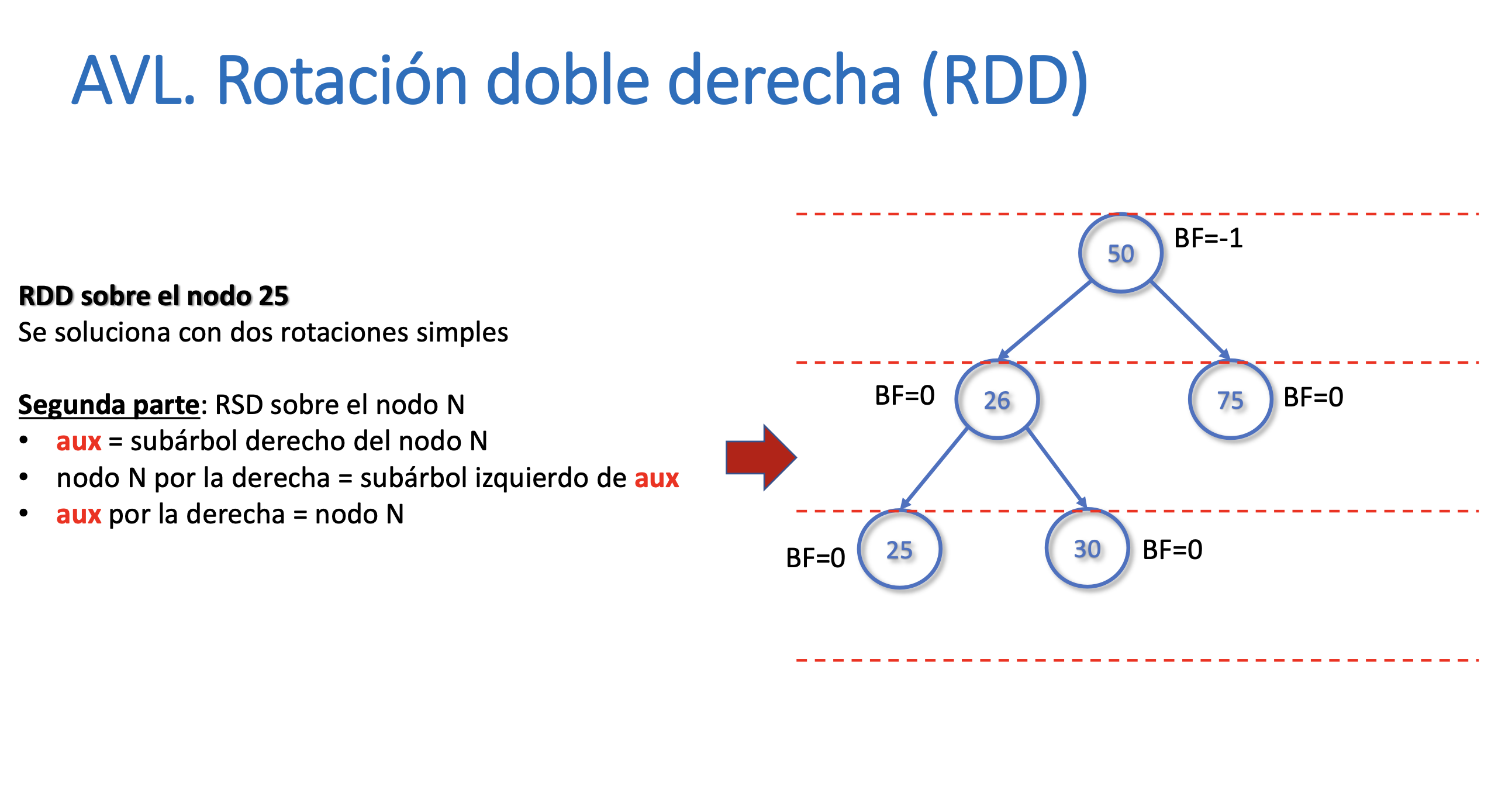
Rotación doble izquierda (RDI)
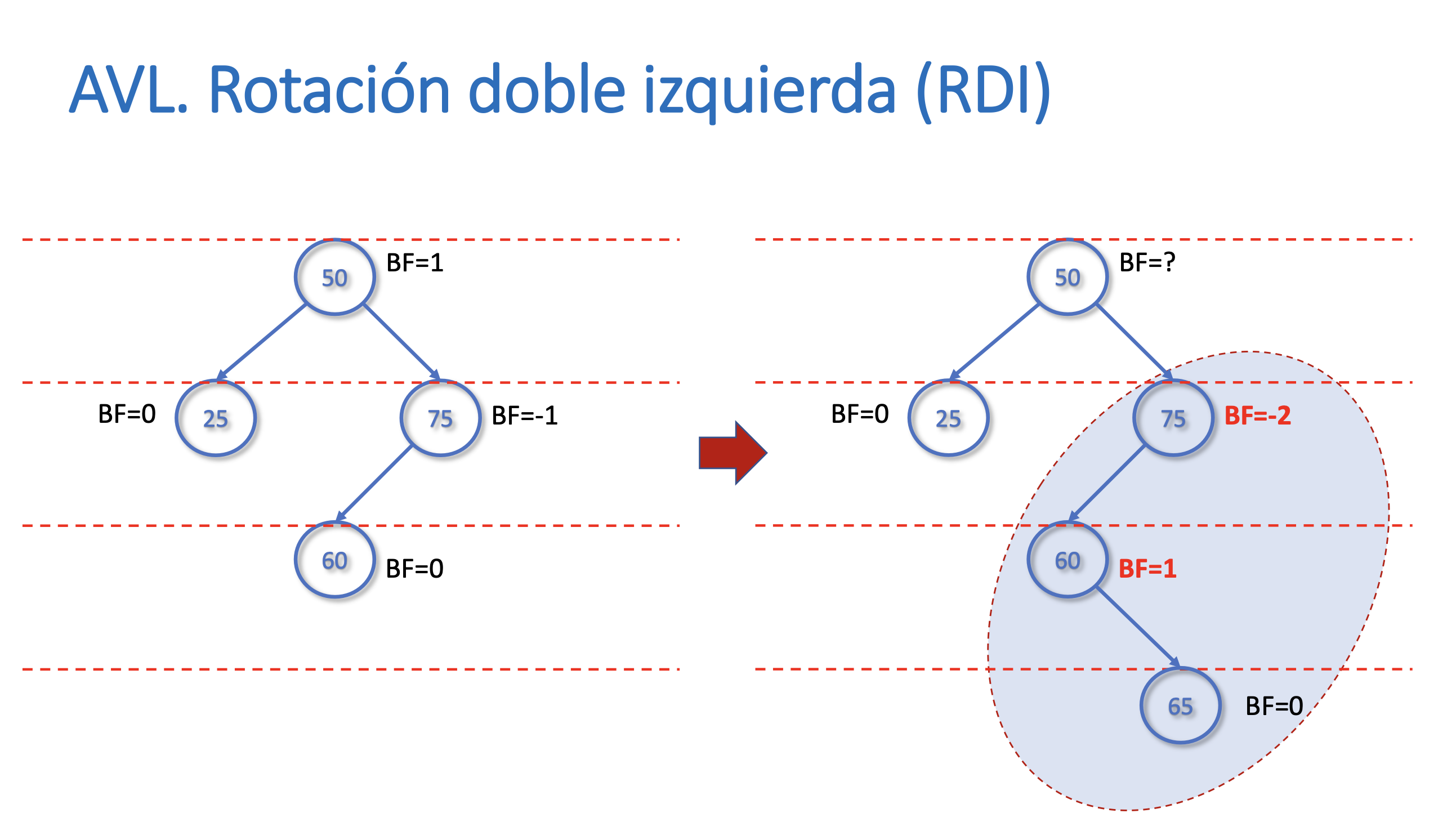
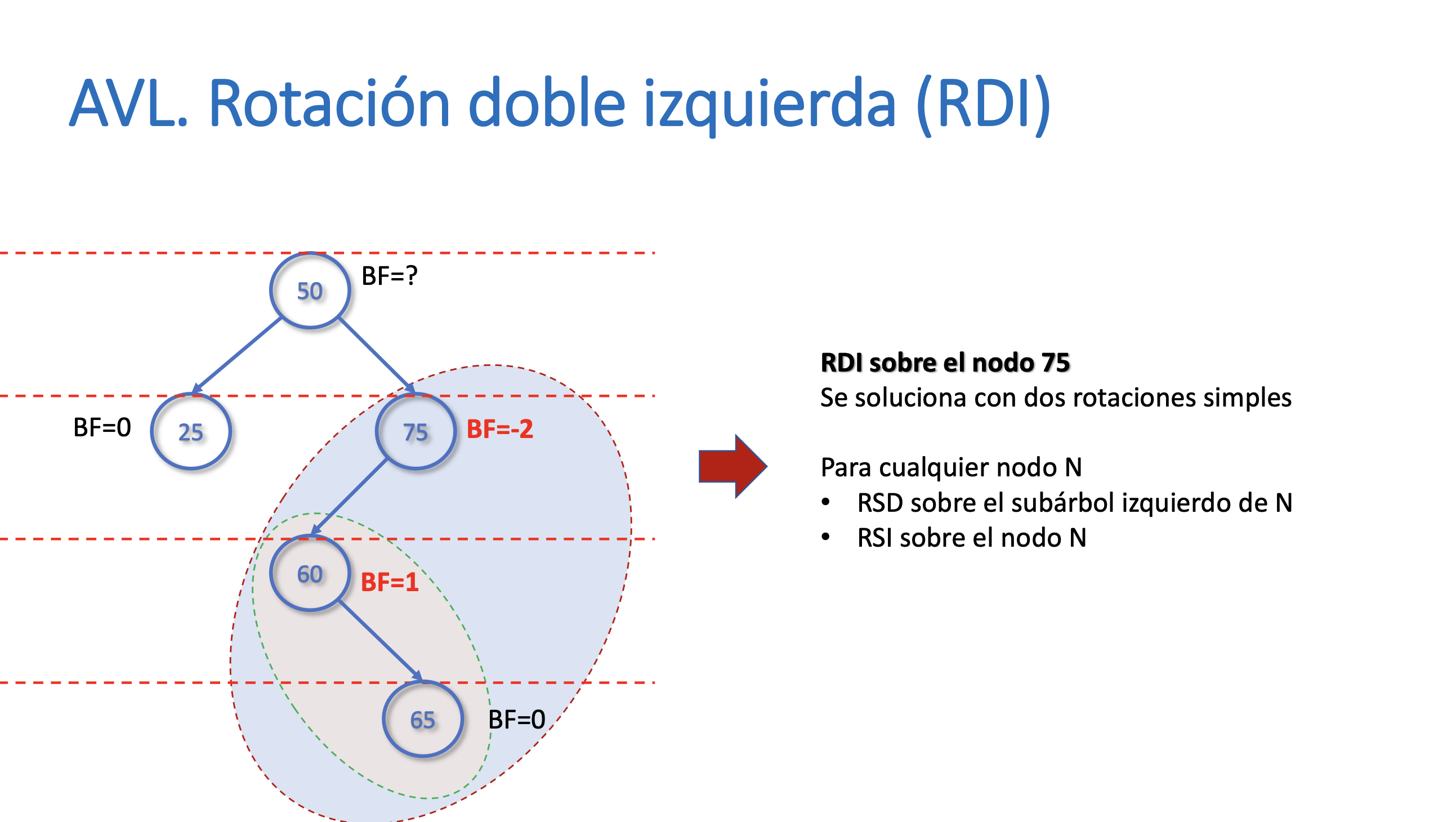
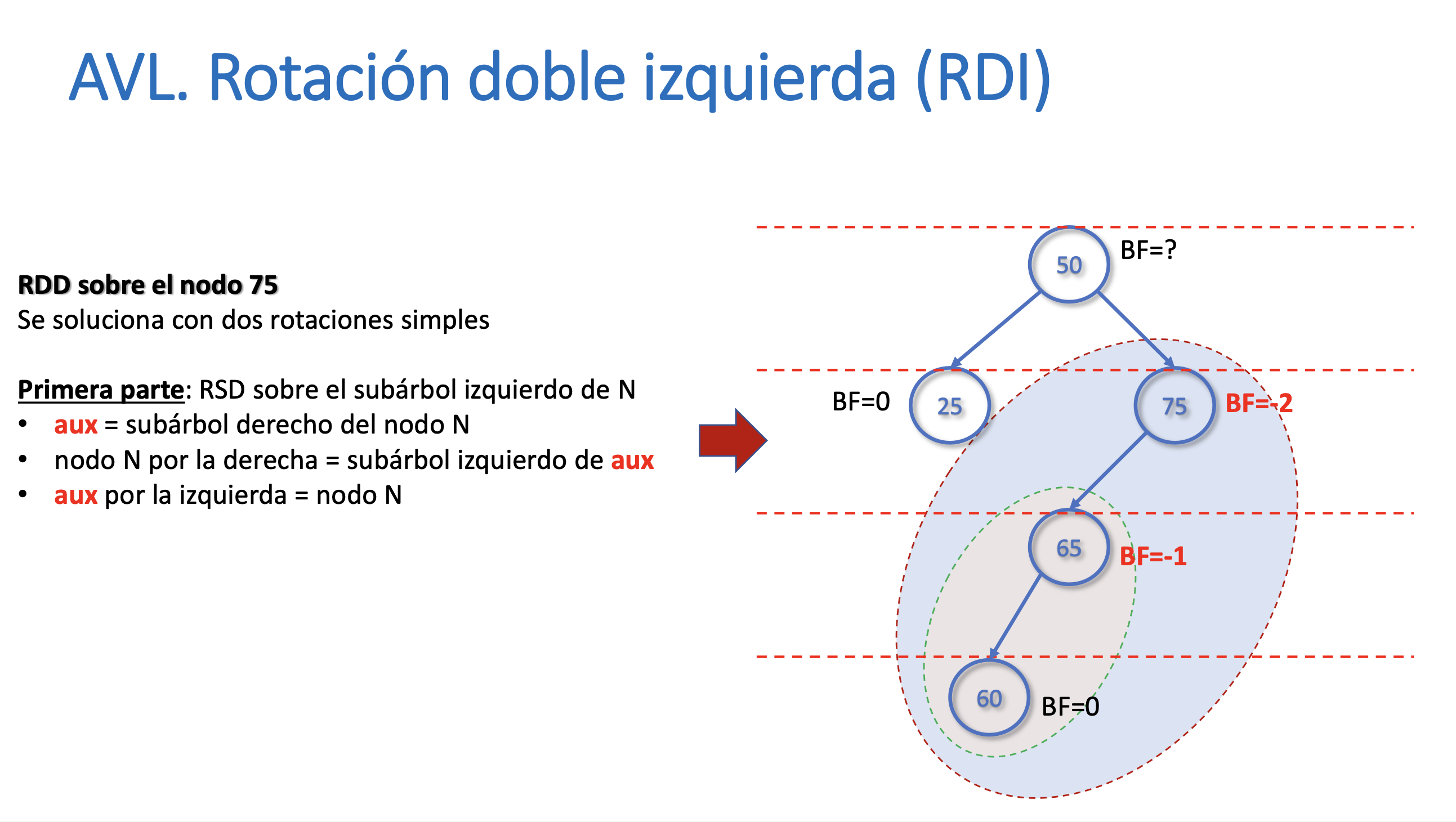
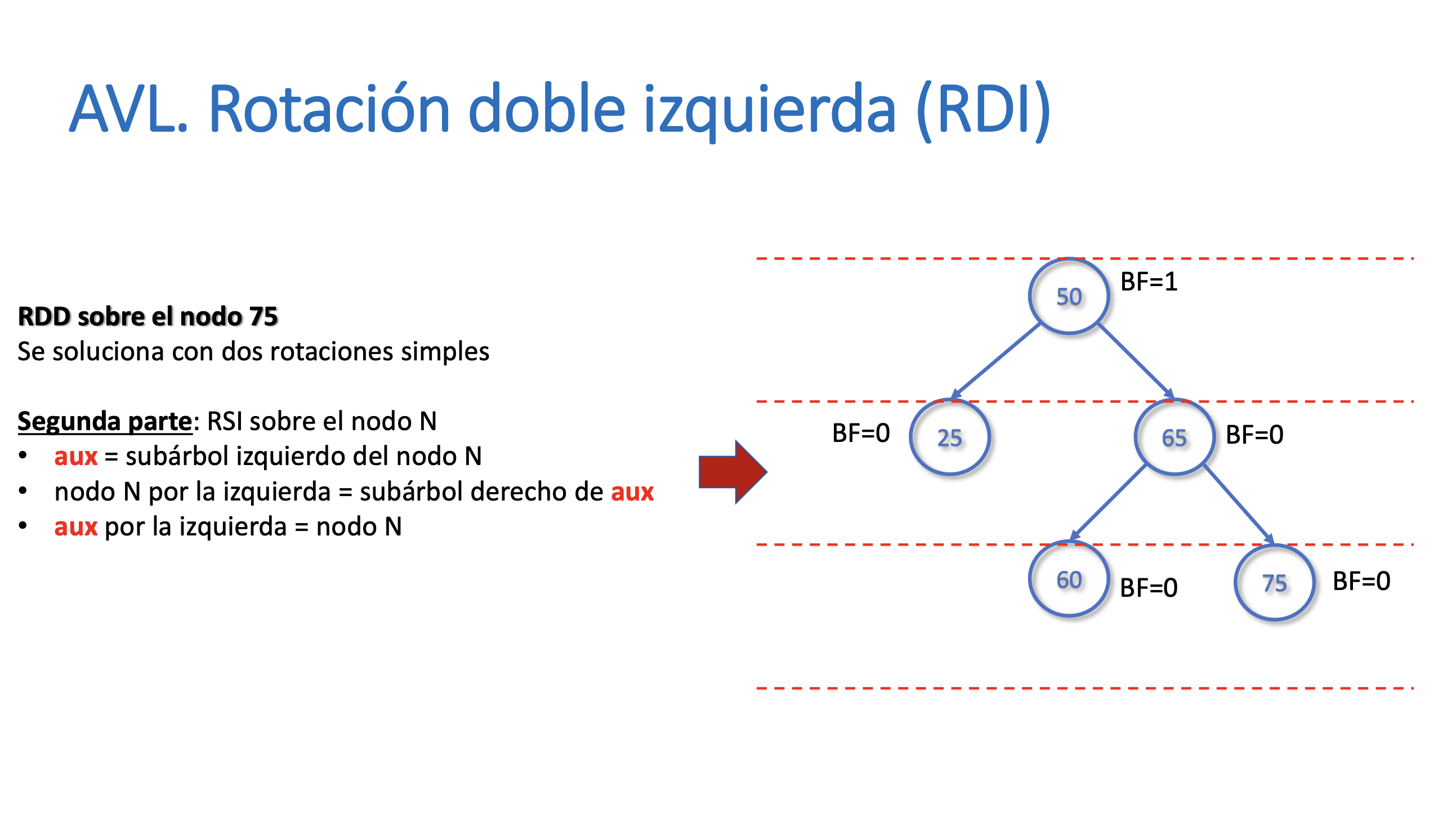
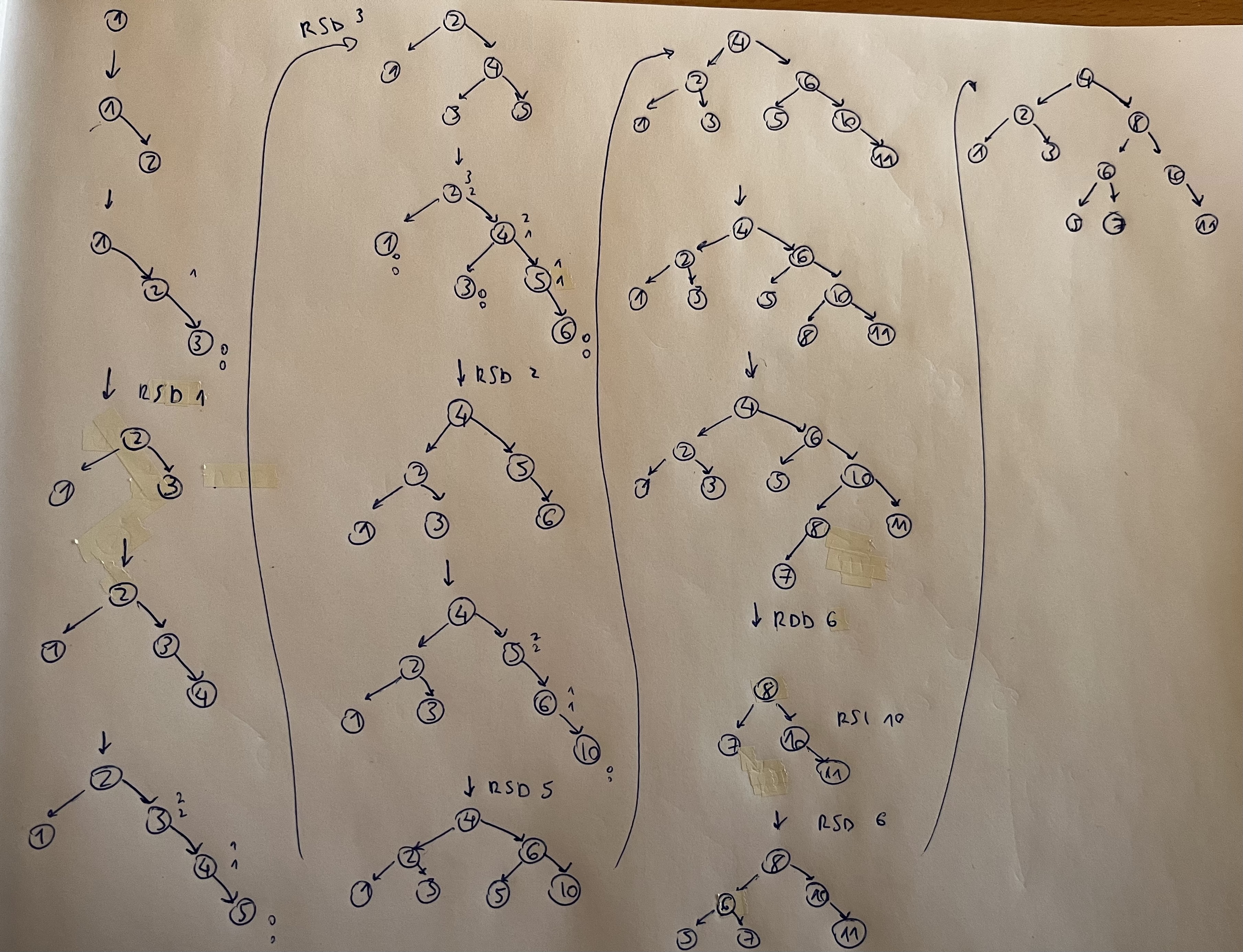
Ejercicios Rotación doble

Borrar una clave de un AVL

Ejercicios Borrado AVL
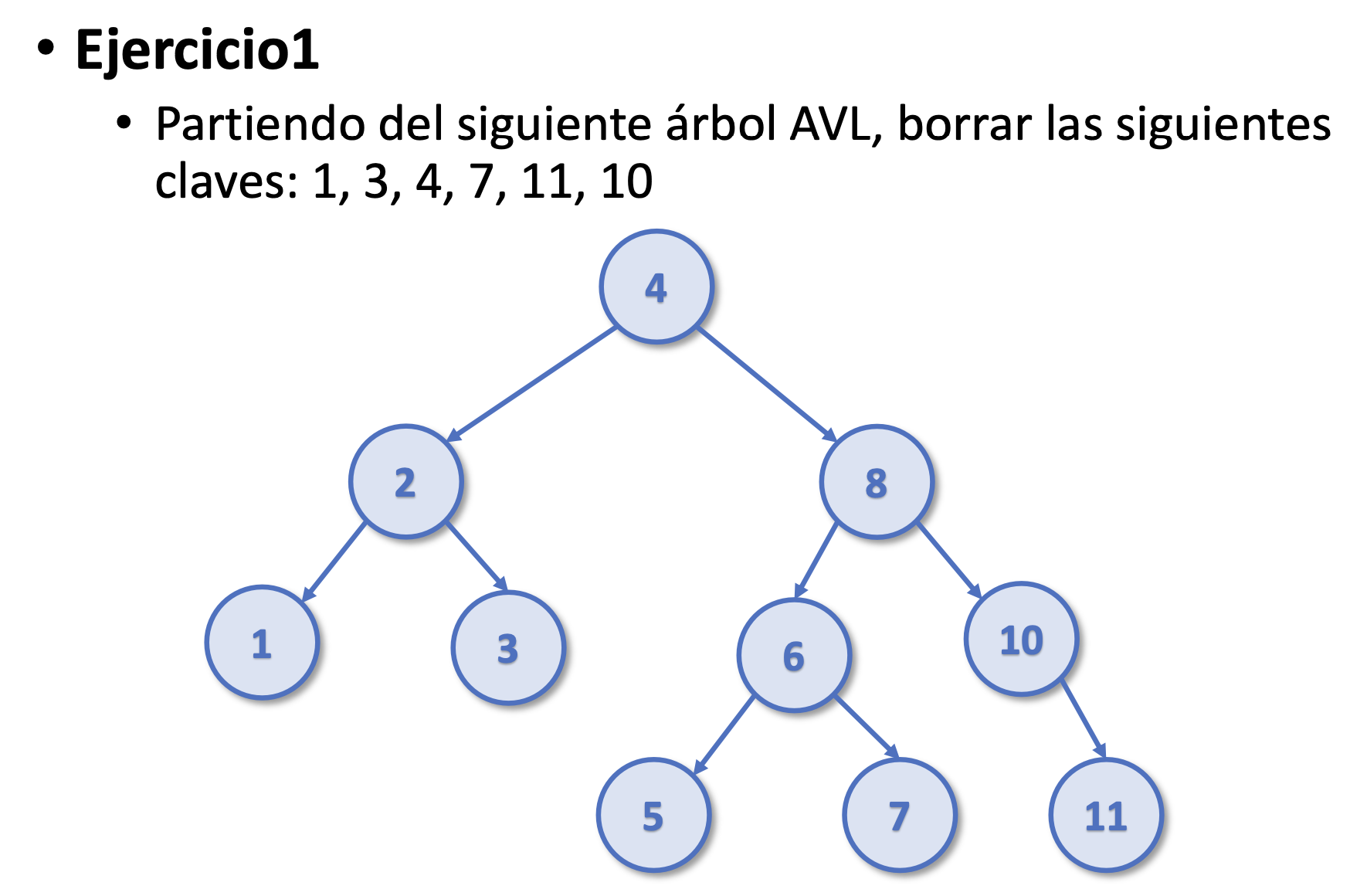
- Está hecho sin borrar el 4 porque no lo vi xd missclick
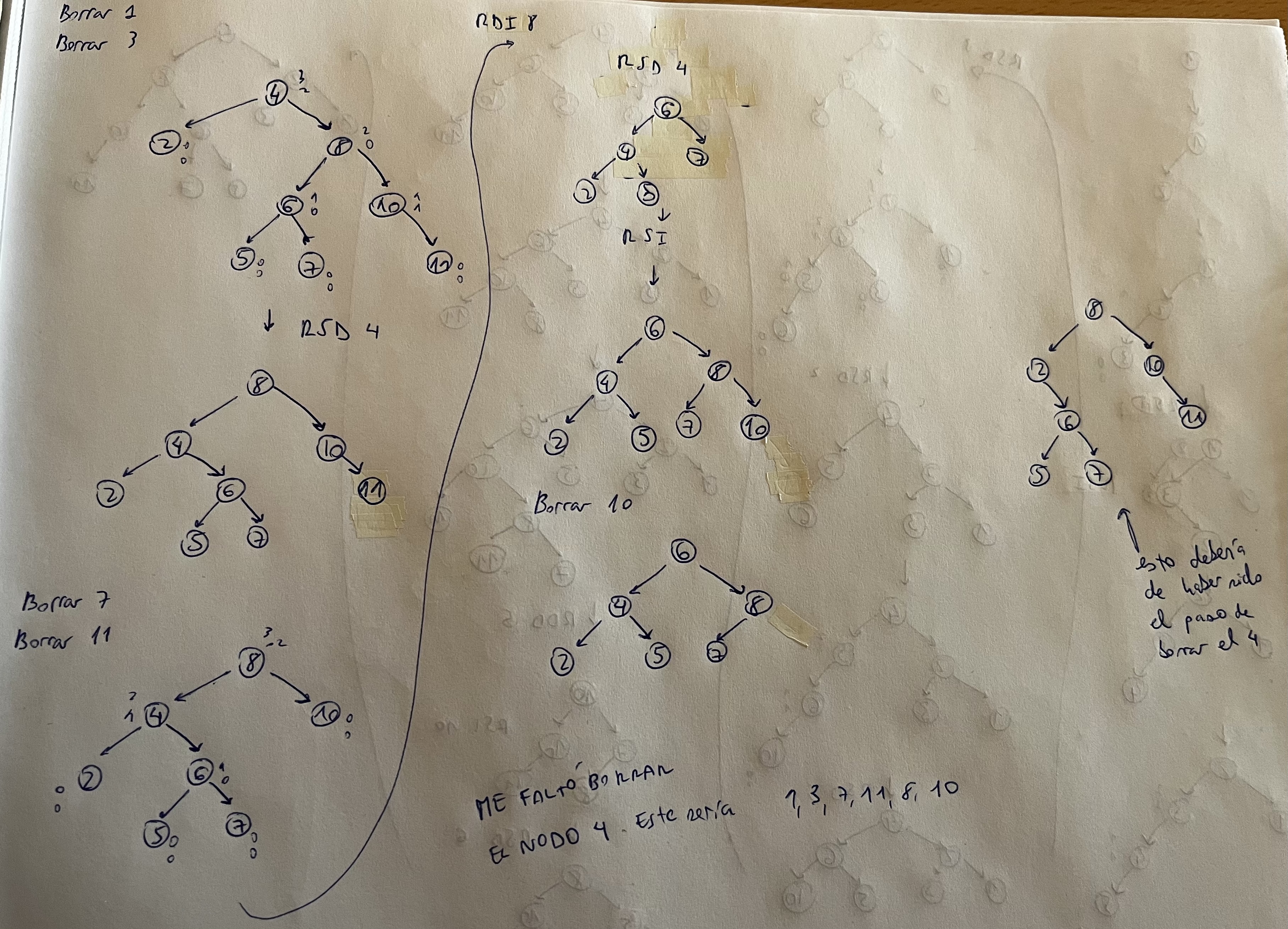
Solucion: 2 5 6 8 (el del ejercicio bien hecho)
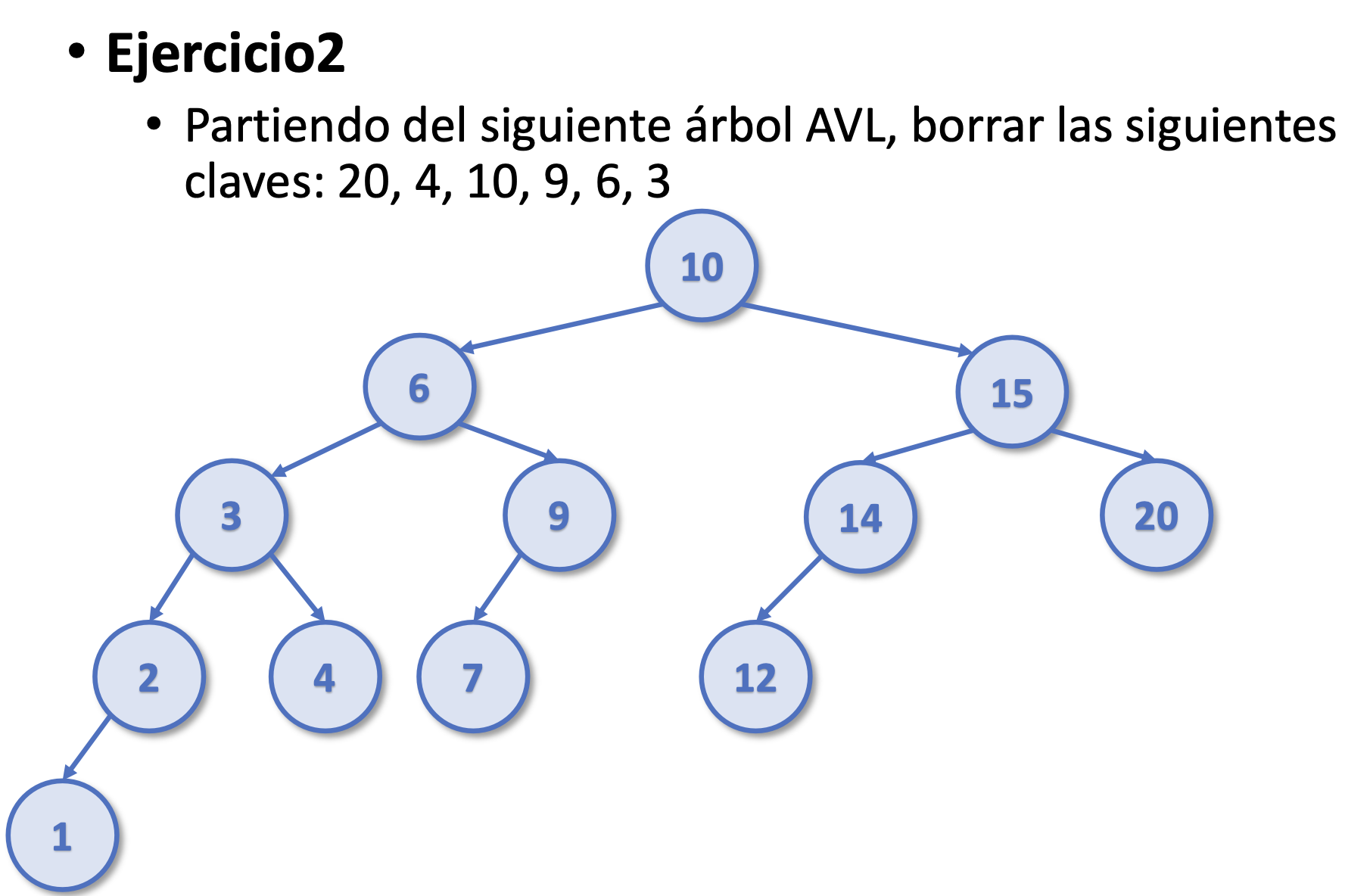
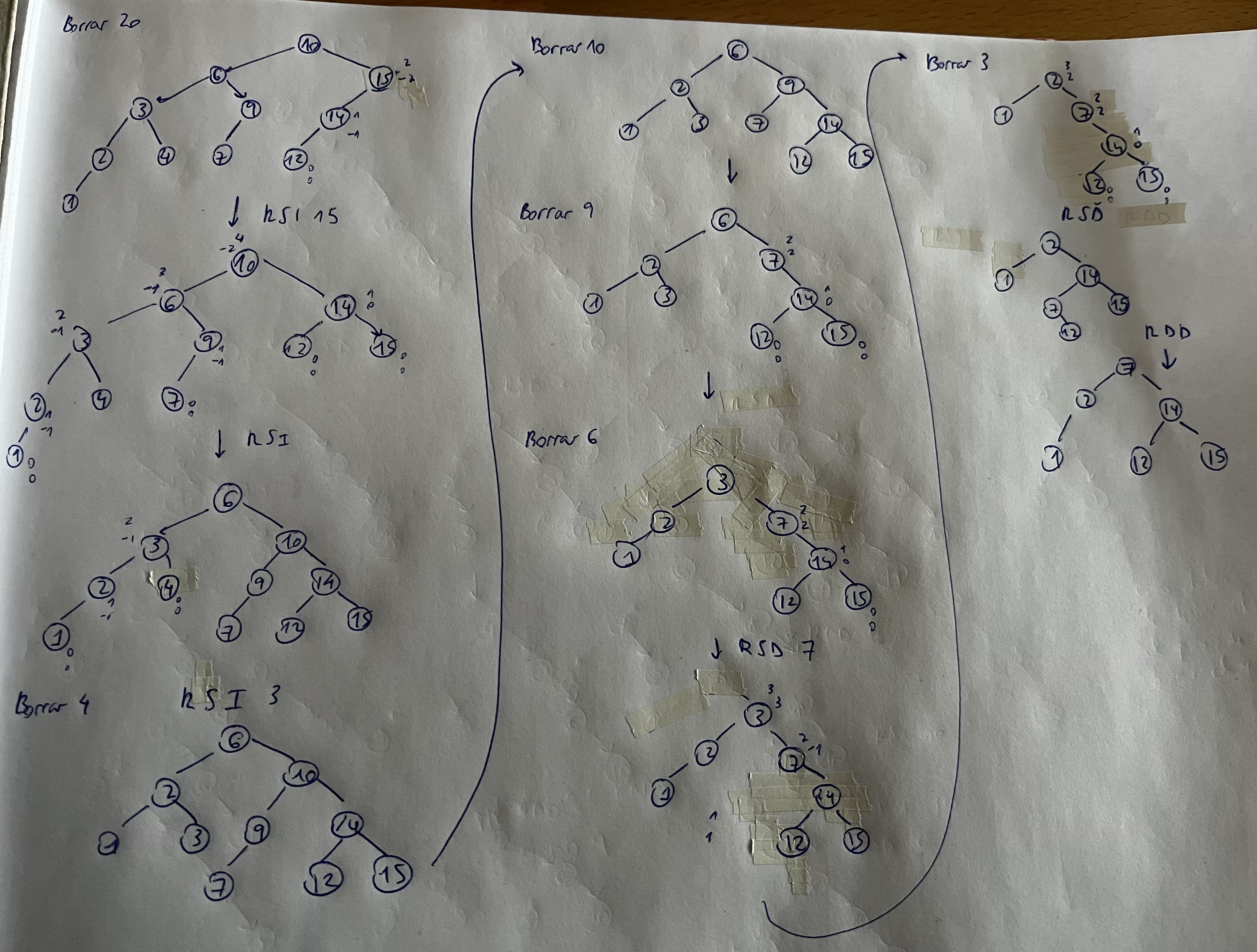
- El caso peor en un árbol avl tiene complejidad O(log(n))
AVL Eficiencia

Colas de prioridad
Montículo binario
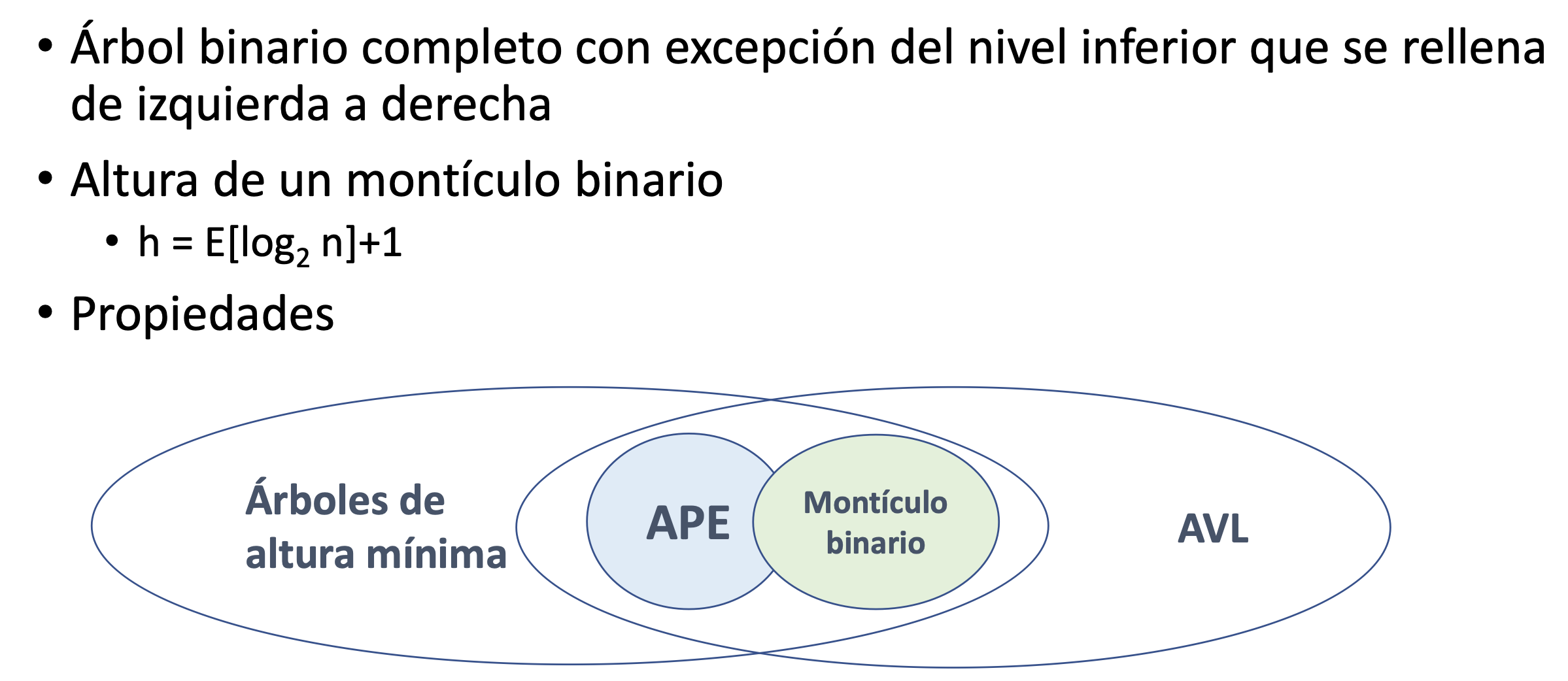
Montículo binario. Propiedades
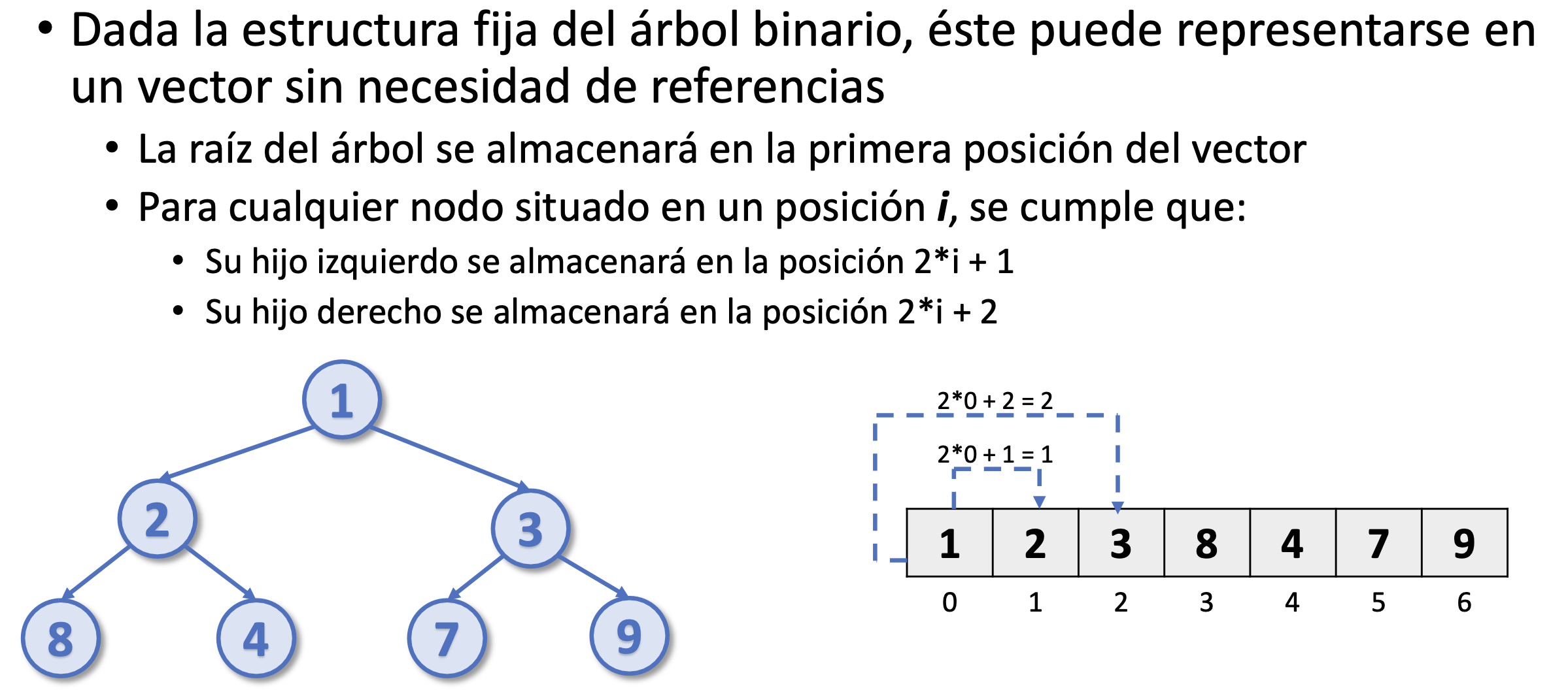
- Siempre se rellena de izquierda a derecha
Montículo binario. Relación de orden

Montículo binario. Operaciones

- Tienen que tener una complejidad logarítmica en el caso peor
Montículo binario. Insertar

Ejercicio 1. Insertar
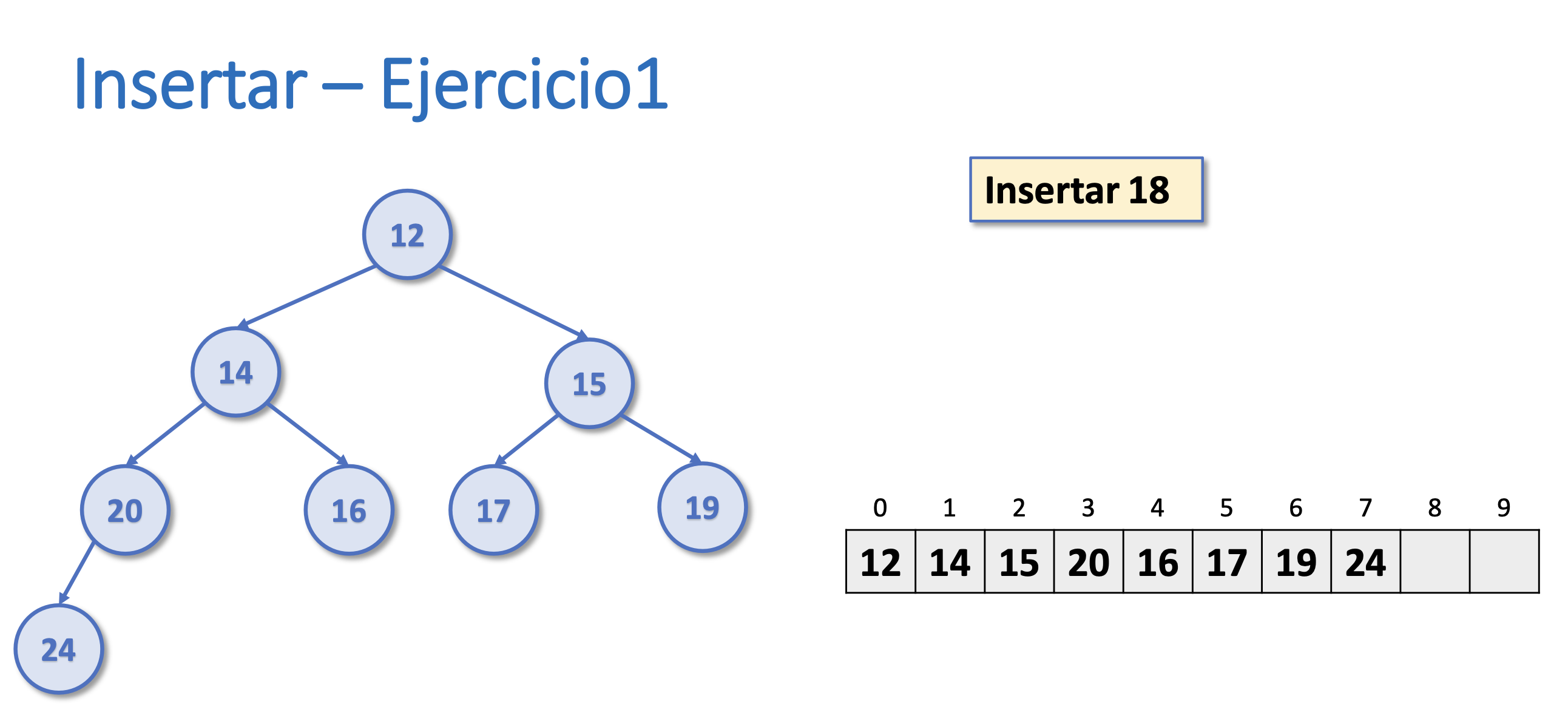
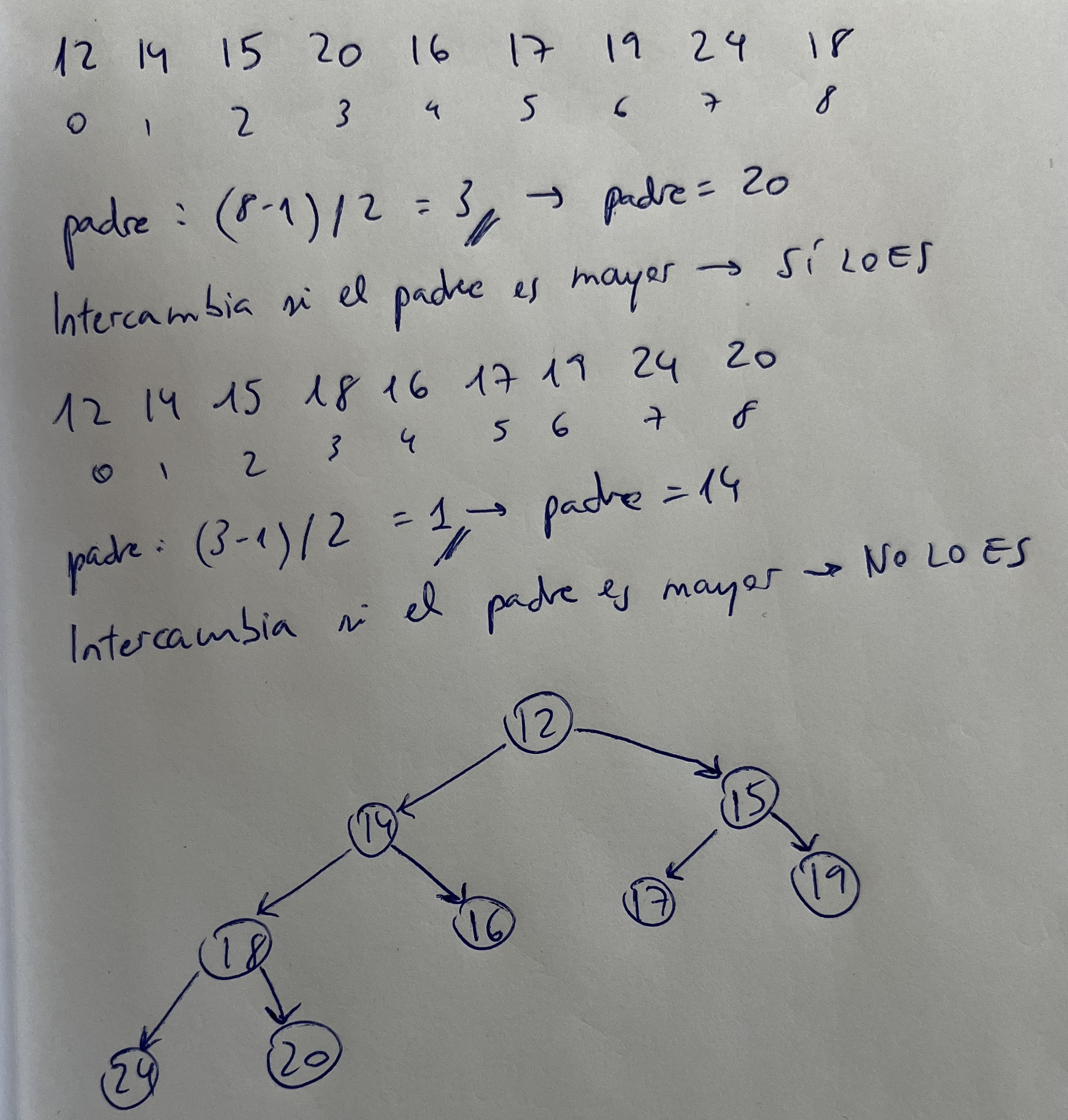
- Los elementos máximos en un montículo binario están situados en los nodos hojas
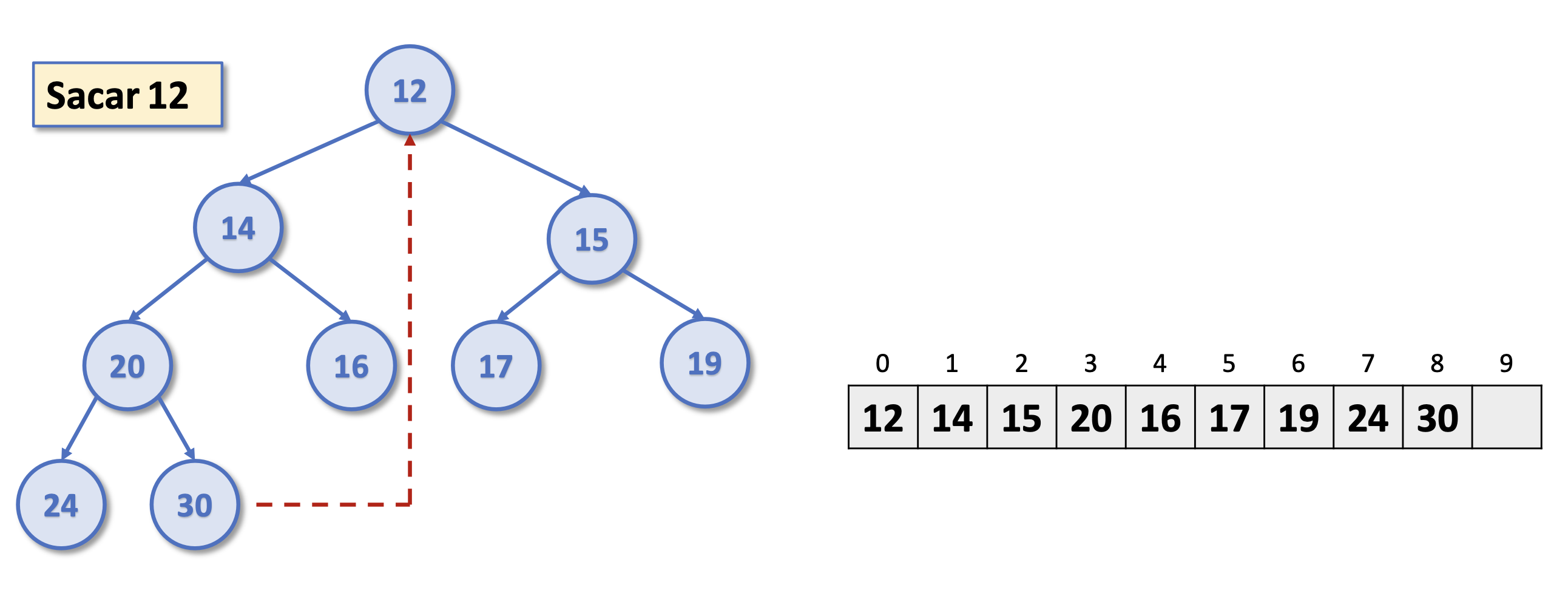
Montículo binario. Sacar

Montículo binario. Devolver el máximo
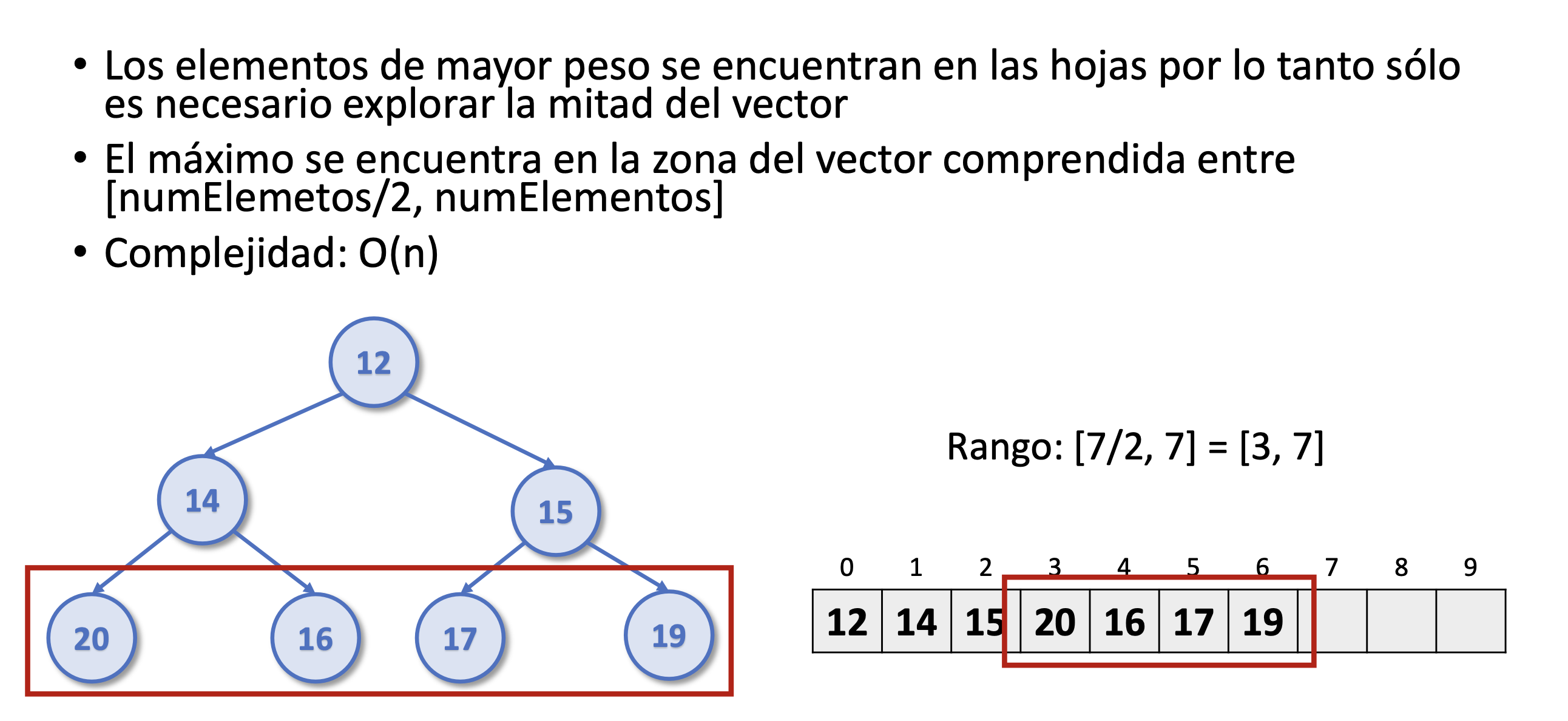
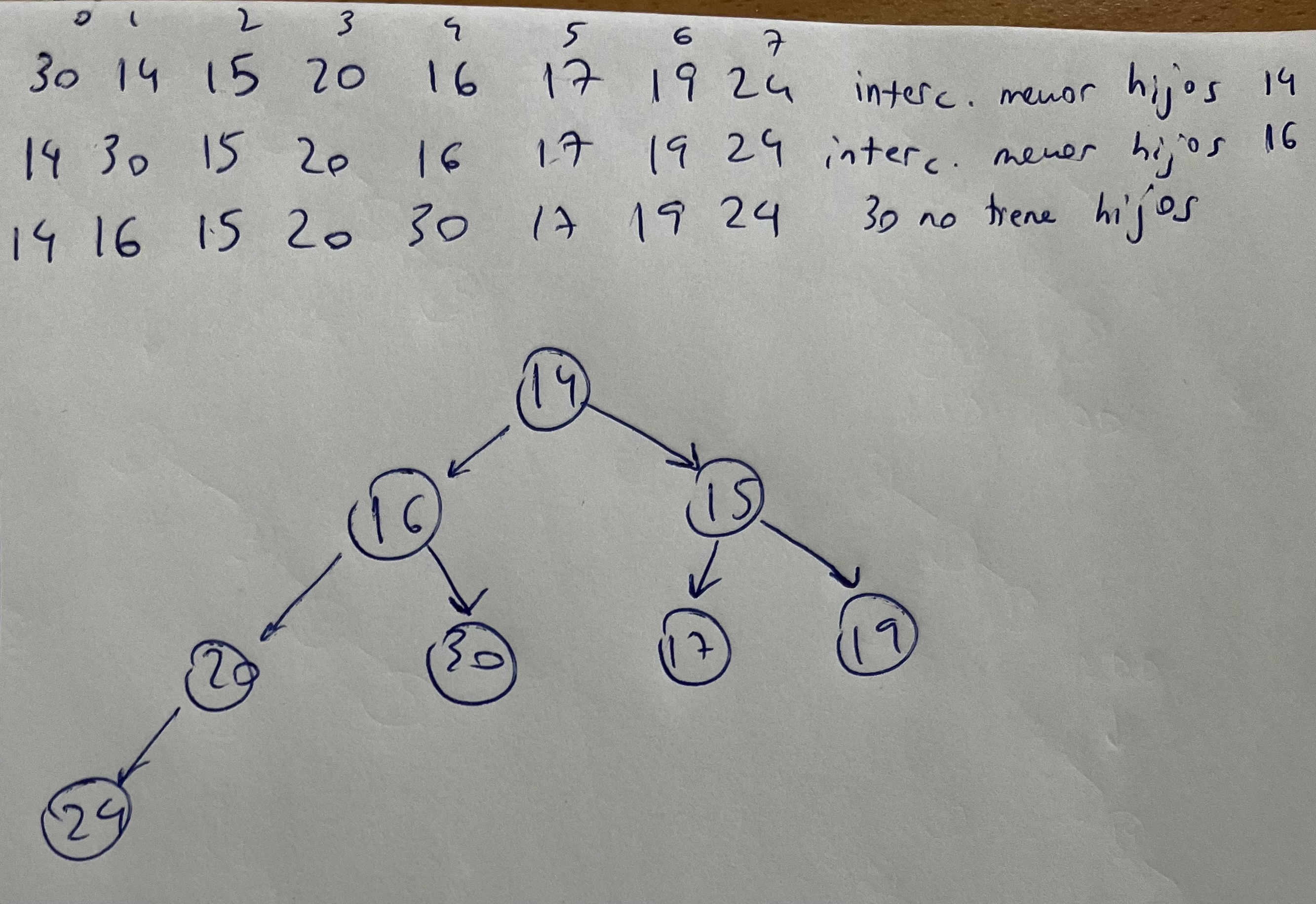
Ejercicio 2. Sacar
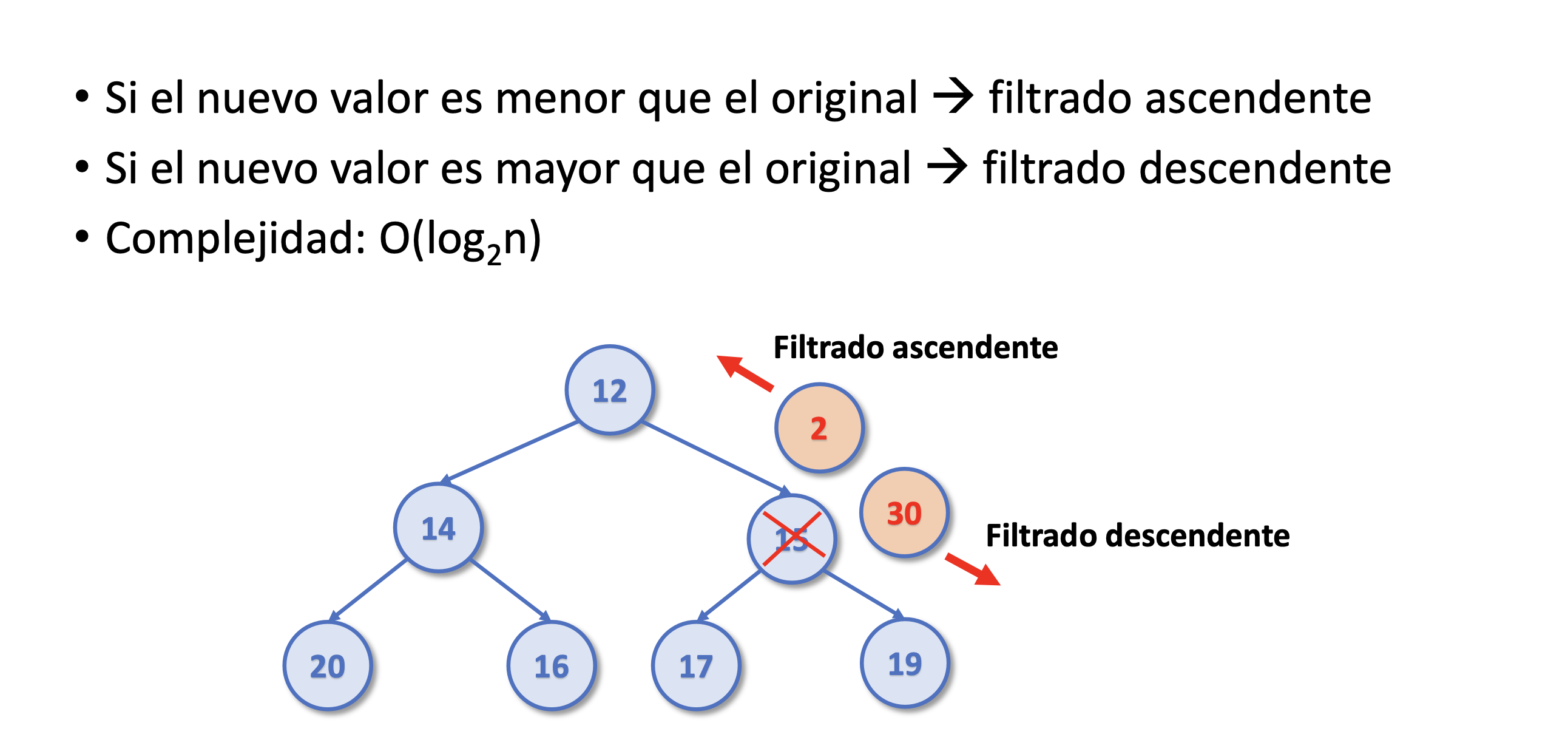
Montículo binario. Cambiar prioridad
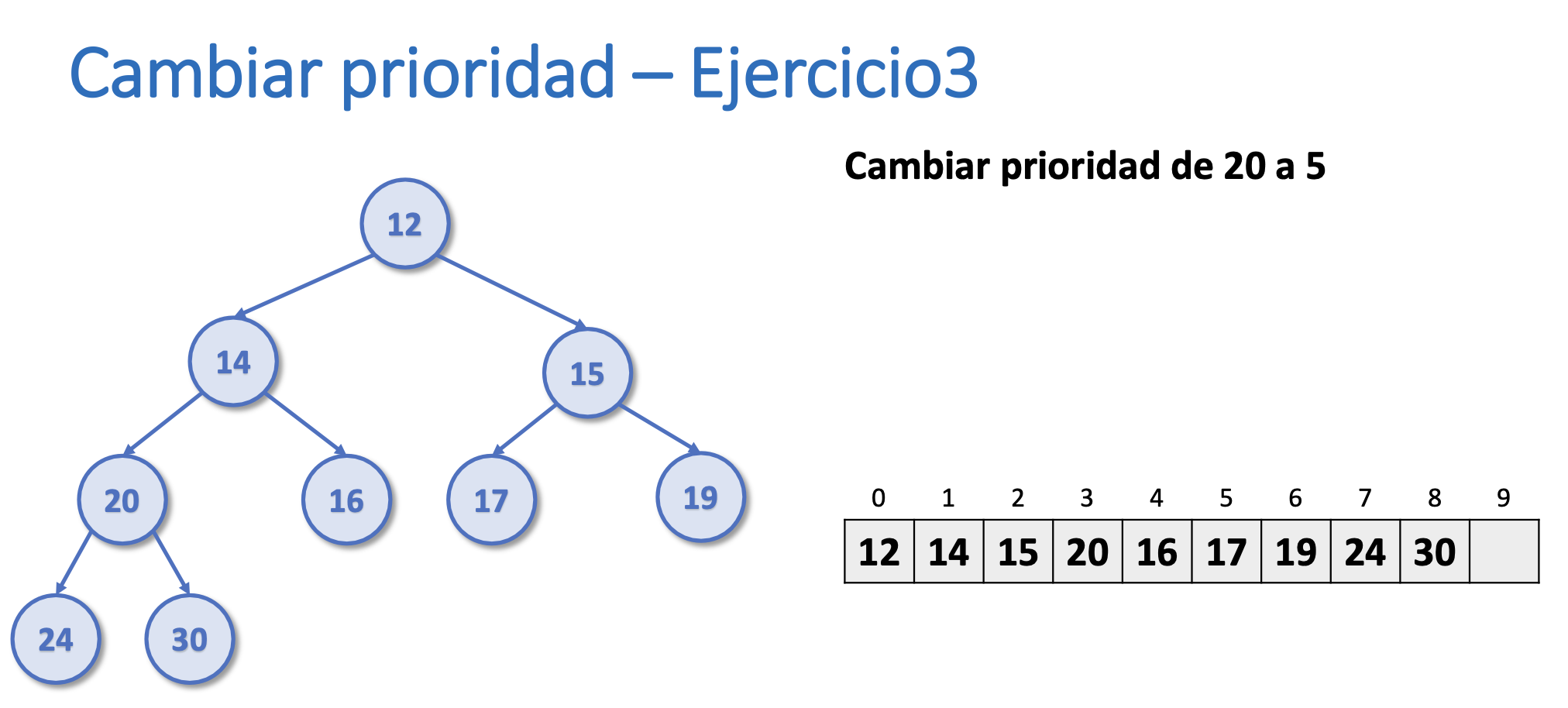
Ejercicio 3. Cambiar prioridad
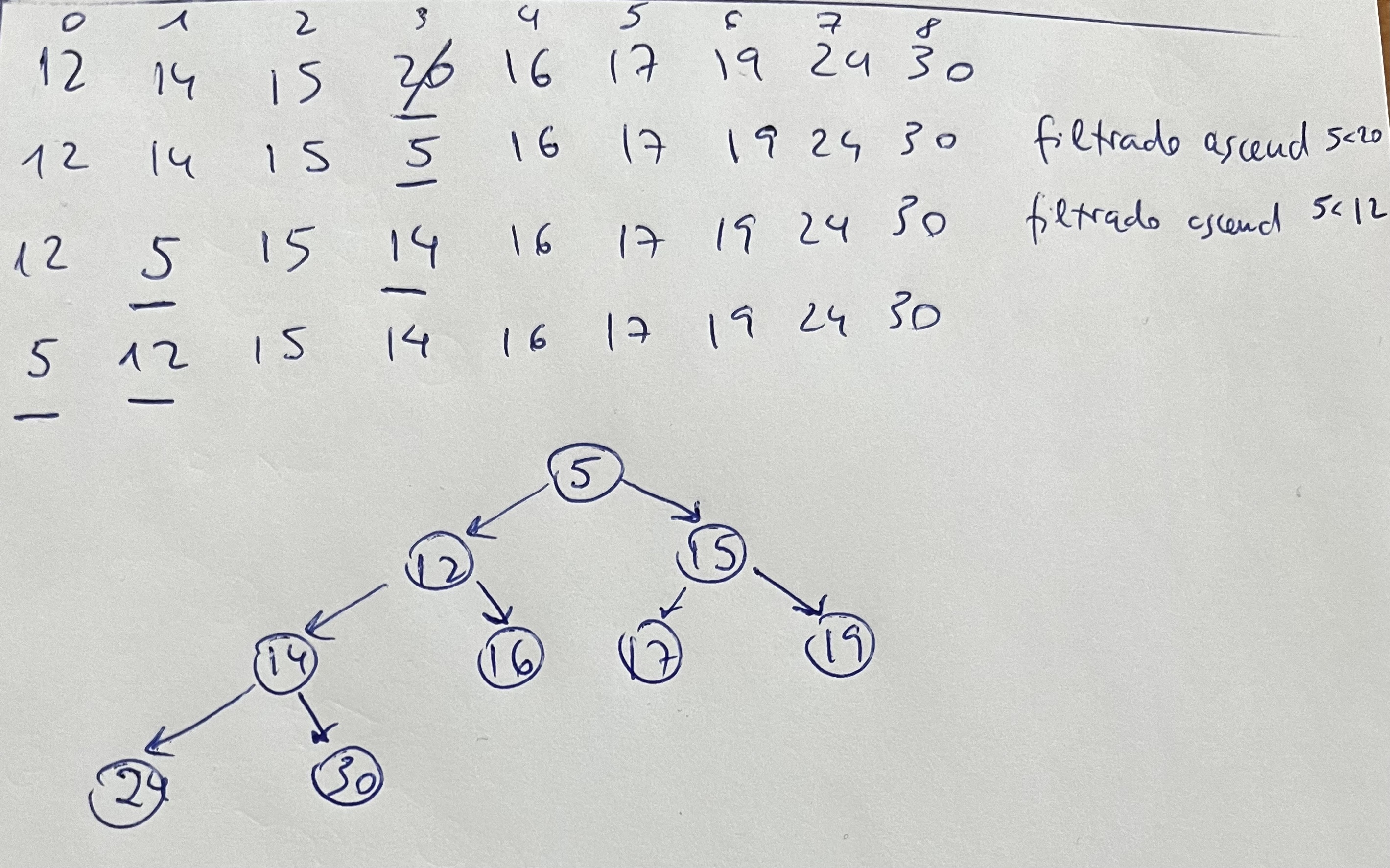
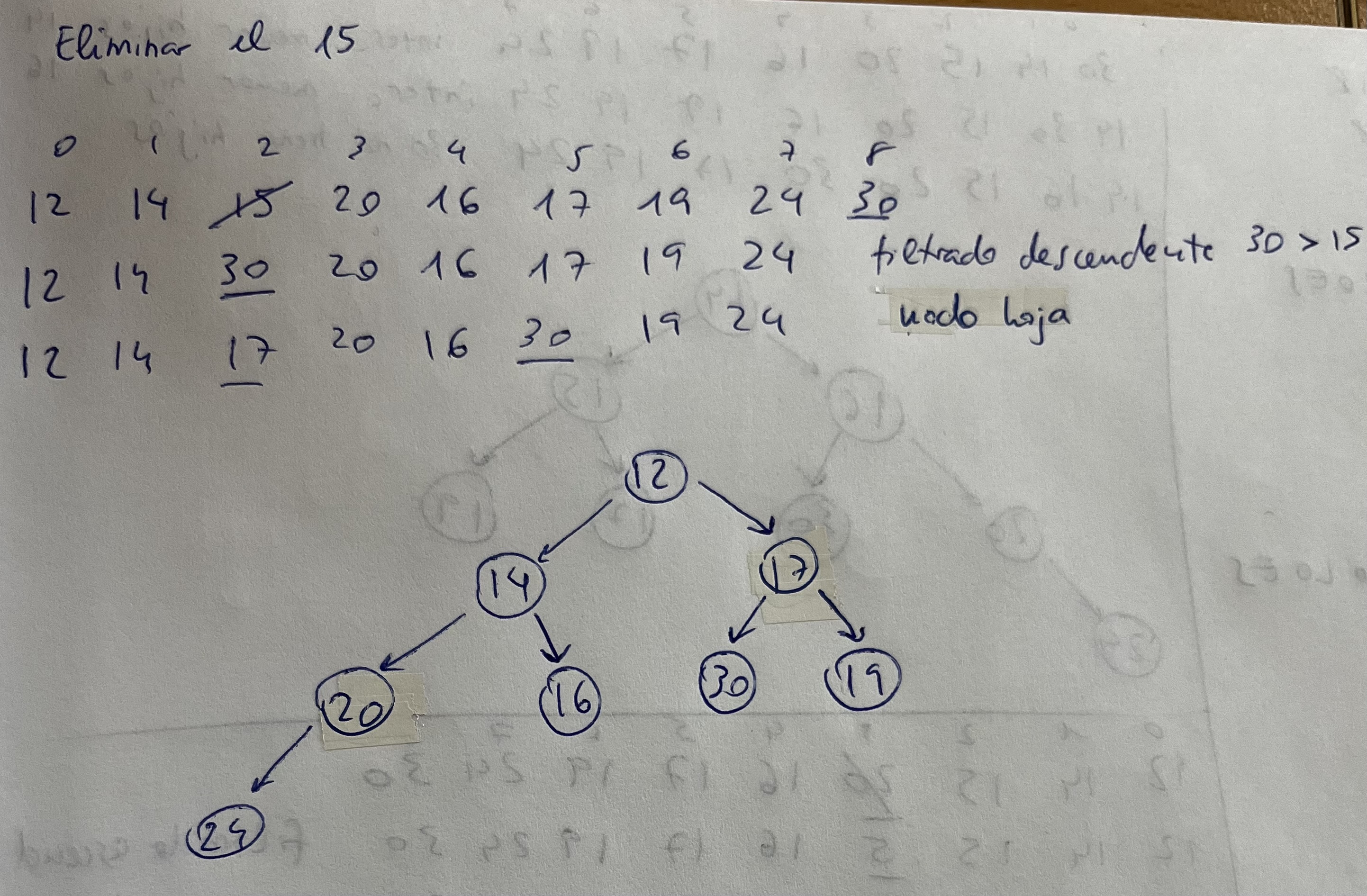
Montículo binario. Eliminar

Ejercicio 4. Eliminar
Ejercicio 5. Insertar
- Insertar: 60, 40, 80, 20, 55, 65, 63, 51, 75, 2, 4, 90, 95, 99, 41, 42, 50, 22, 30, 25, 31, 32, 33, 36, 38, 39
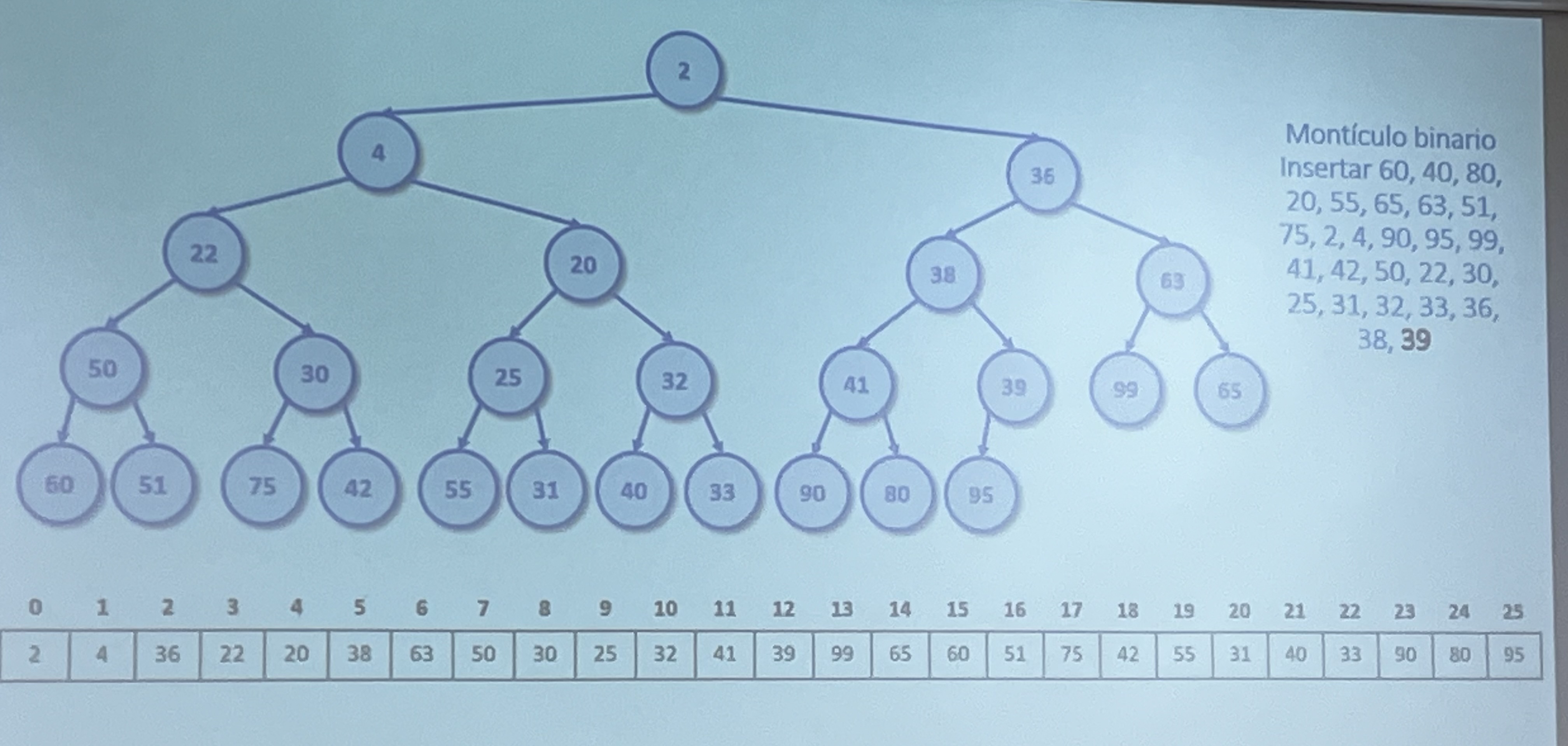
- Ir siguiendo este procedimiento:

Ejercicio 6. Borrar
- Borrar 99, 38, 22 y 2 (del ejercicio anterior)
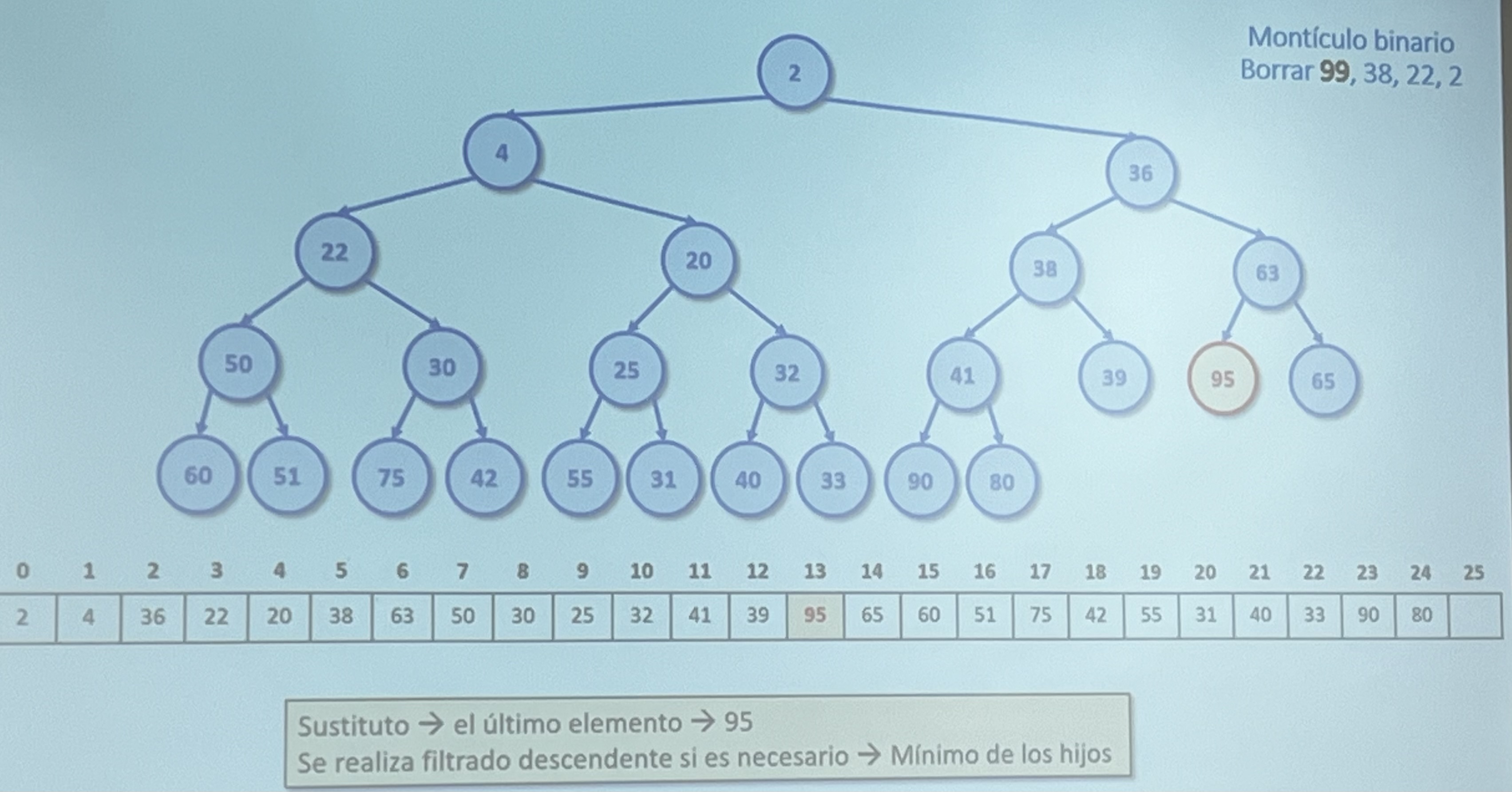
Árboles B
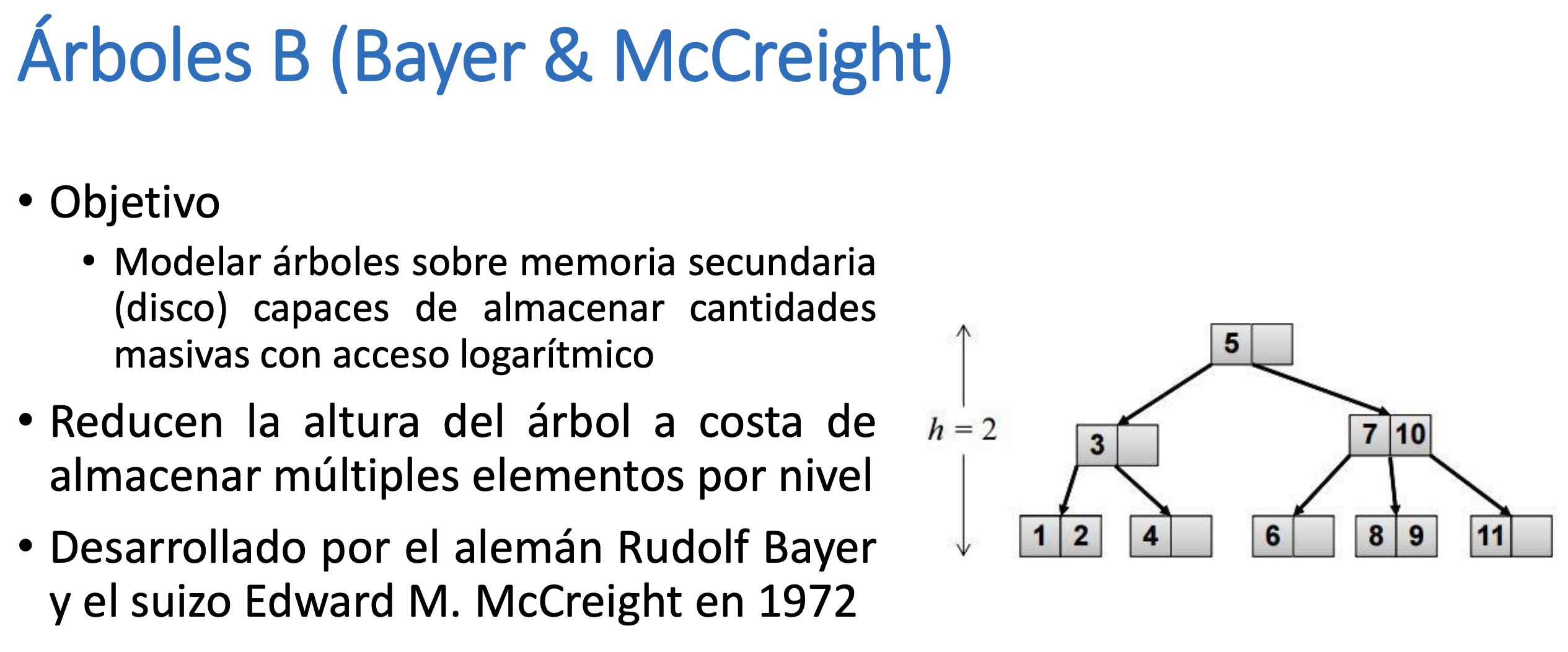
Árbol B de orden n

Árbol B de orden 2 Ejemplo
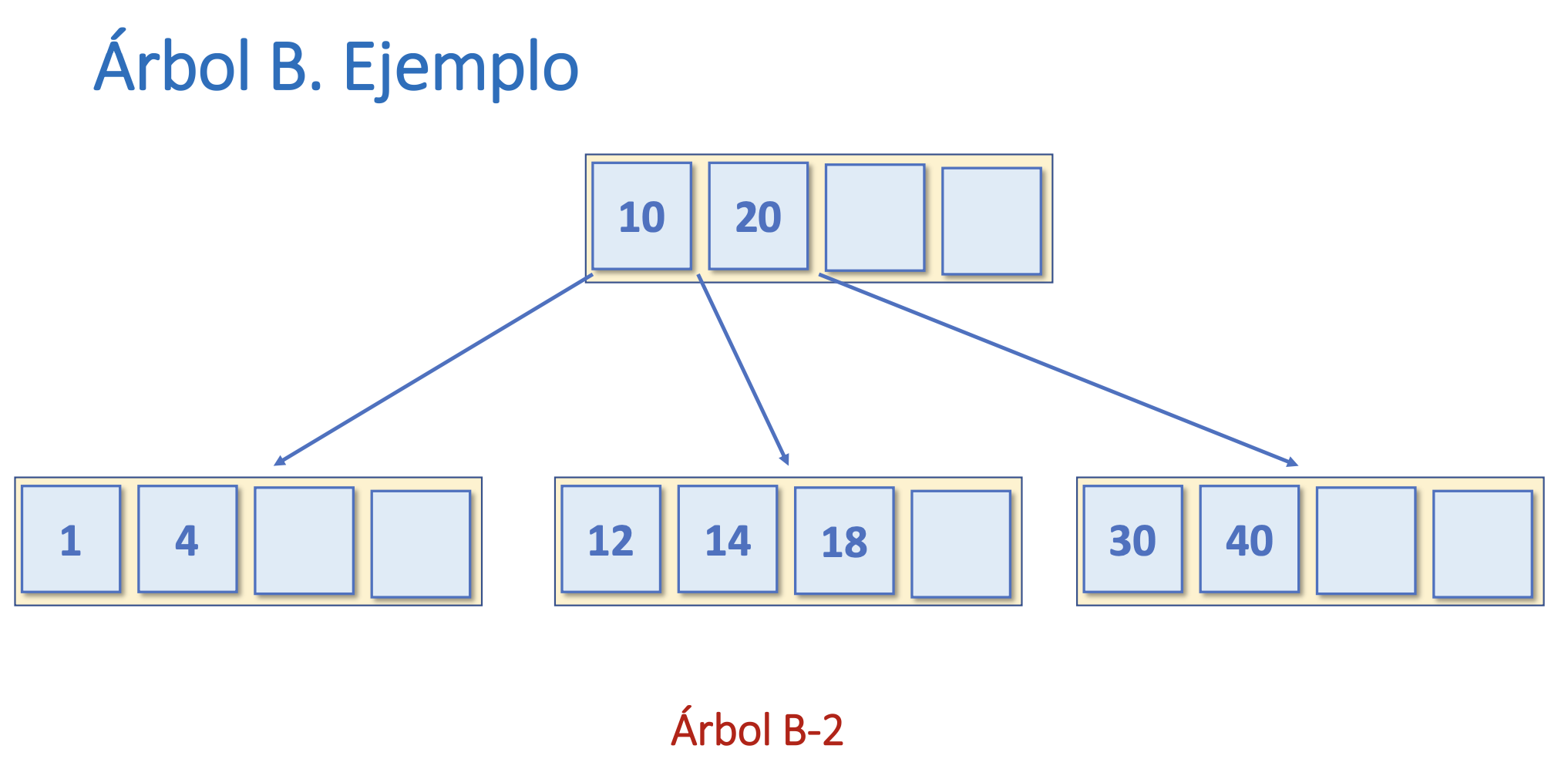
- Si es de orden 2, tiene 3 páginas
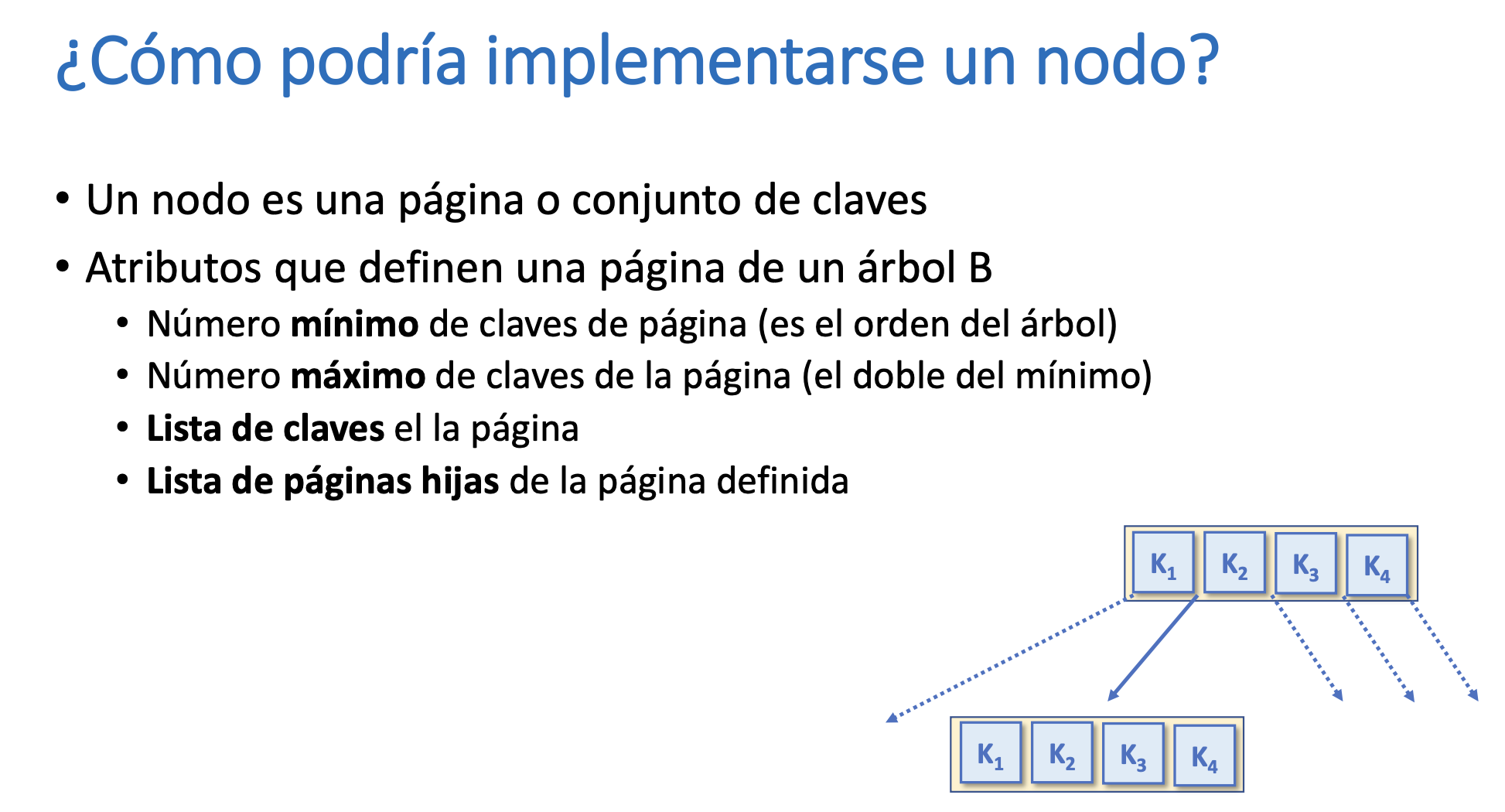
¿Cómo se implementa un nodo?
Capacidad mínima de un árbol B
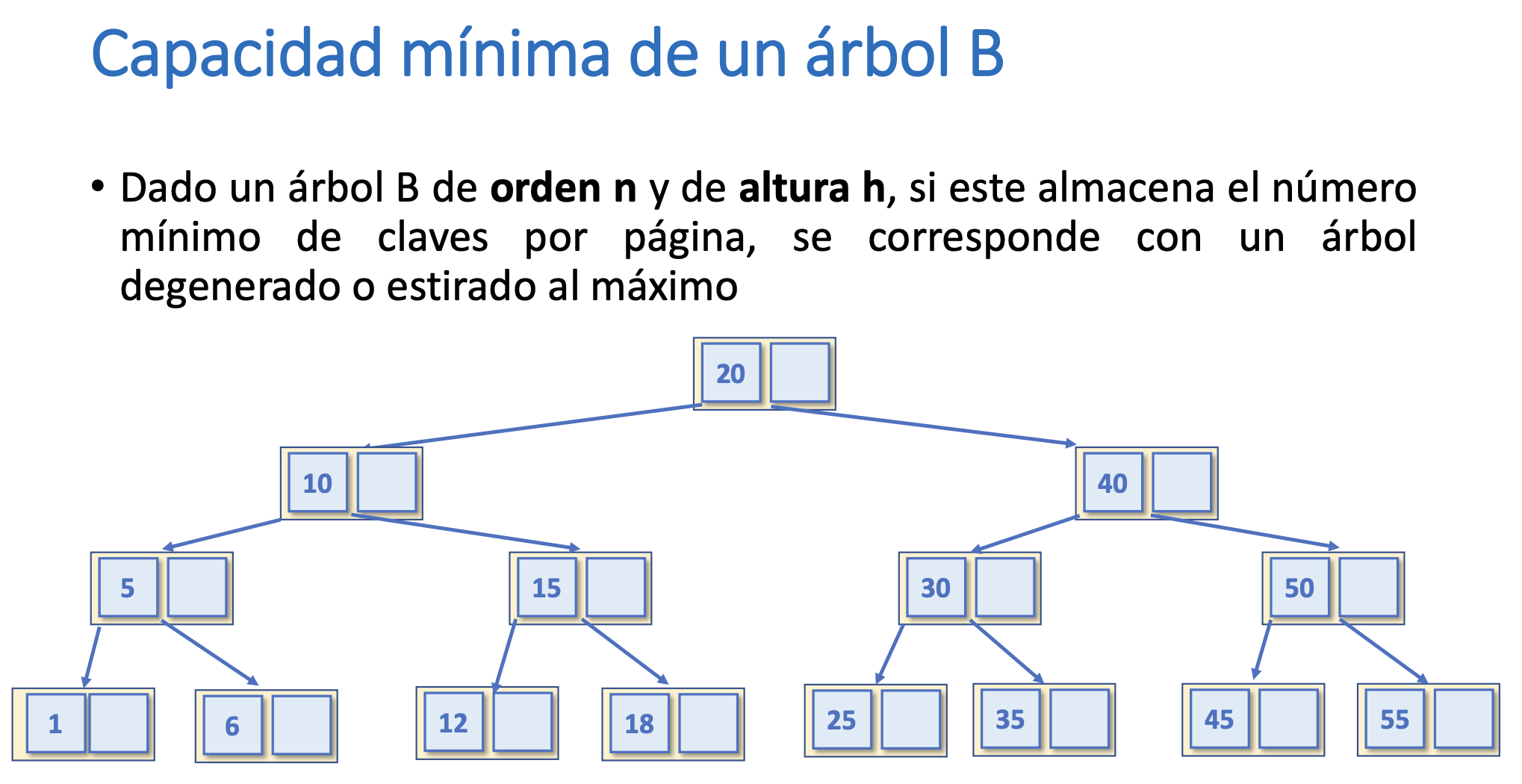
Cálculo de la capacidad mínima de las claves

Altura máxima de un árbol B

Capacidad máxima de un árbol B
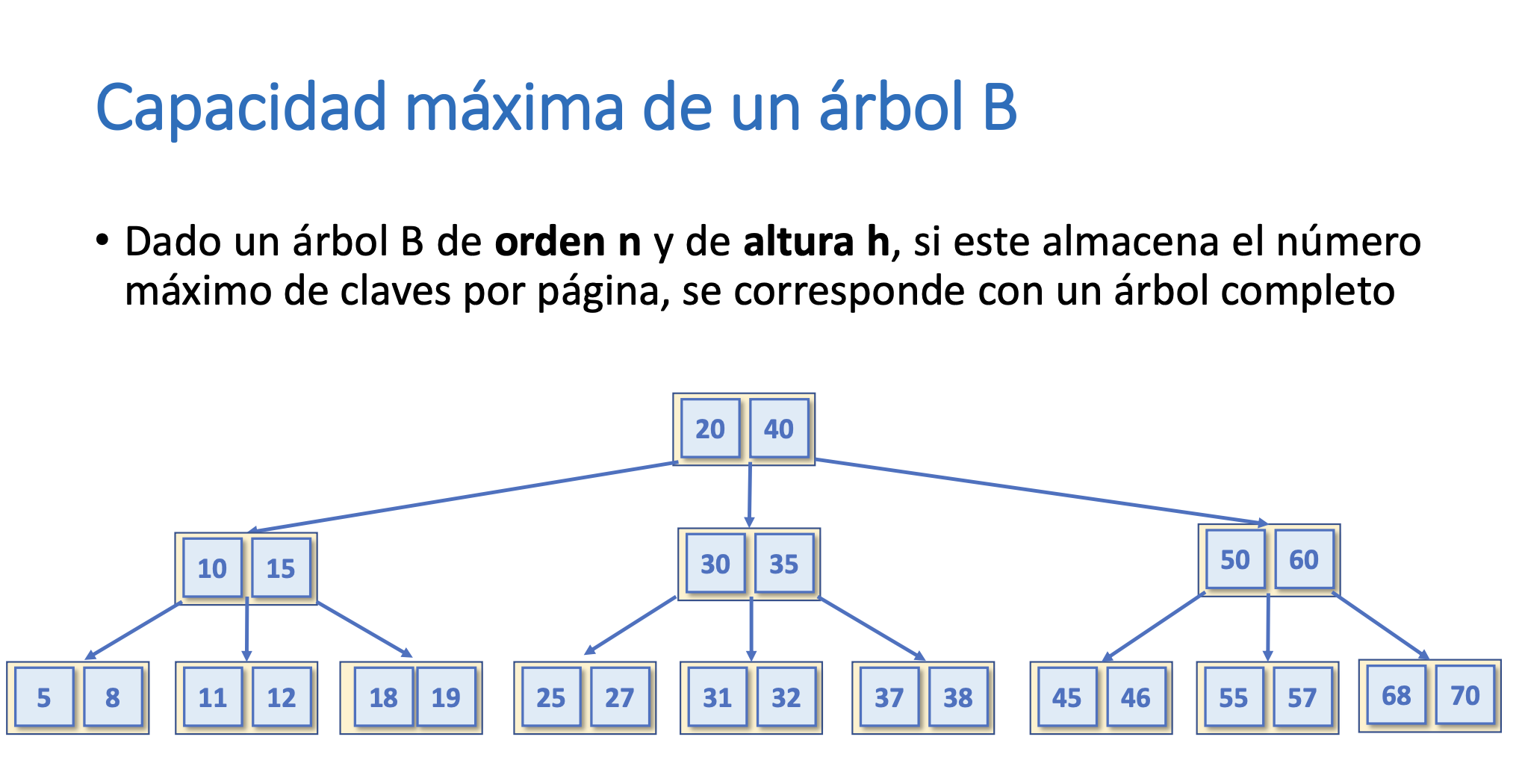
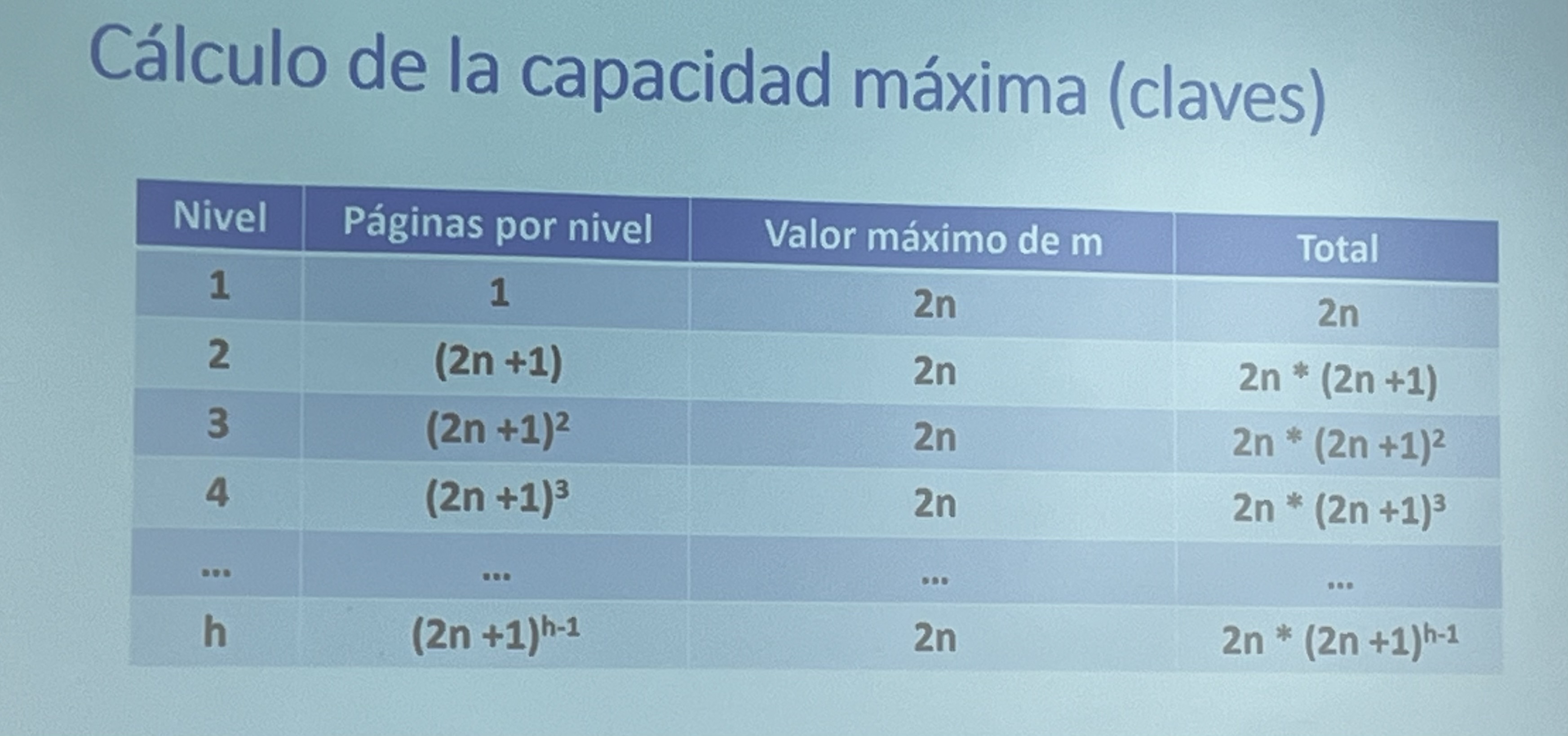
Cálculo de la capacidad máxima
Altura mínima de un árbol B

Árbol B. Buscar

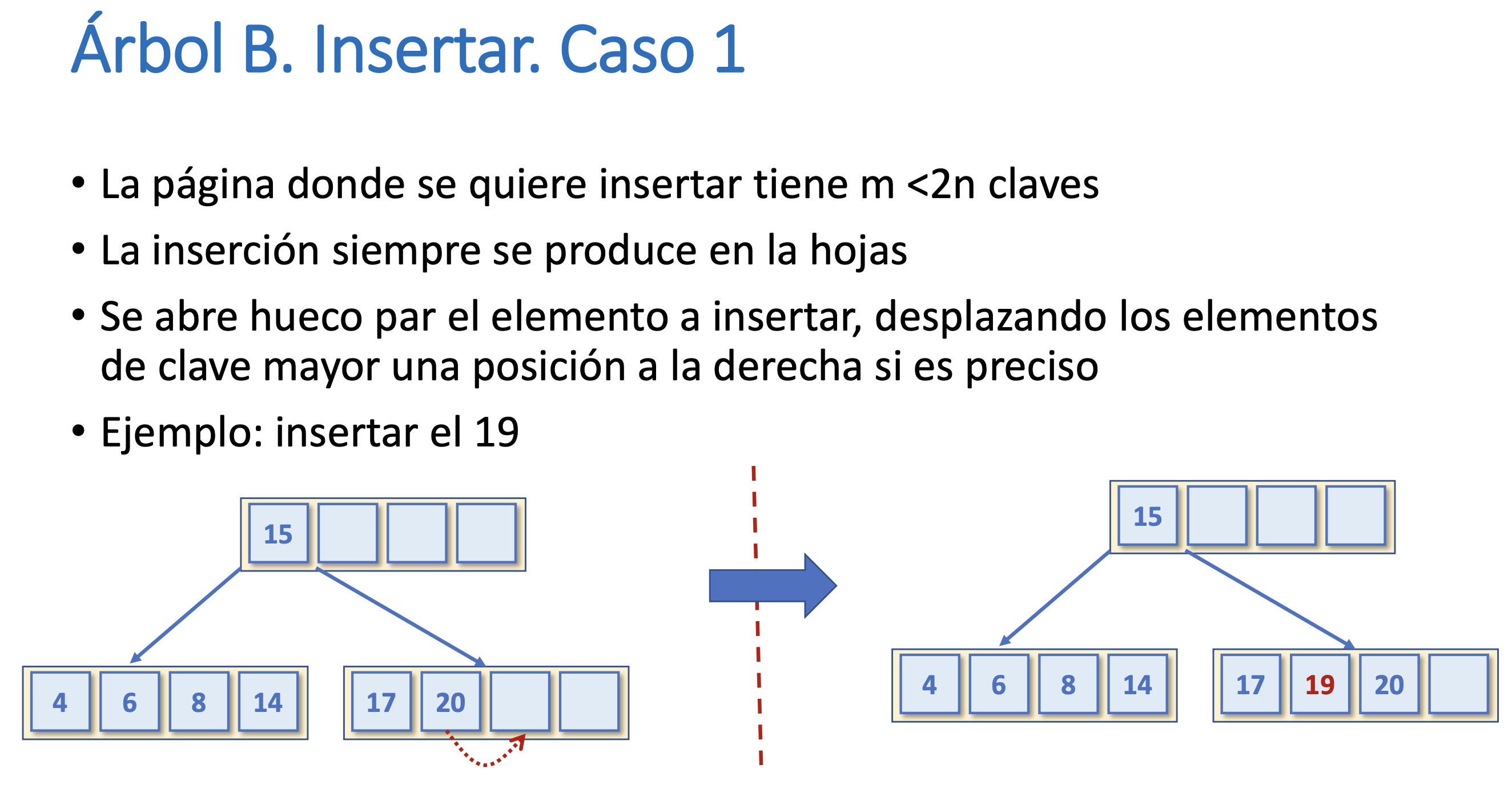
Árbol B. Insertar. Caso 1
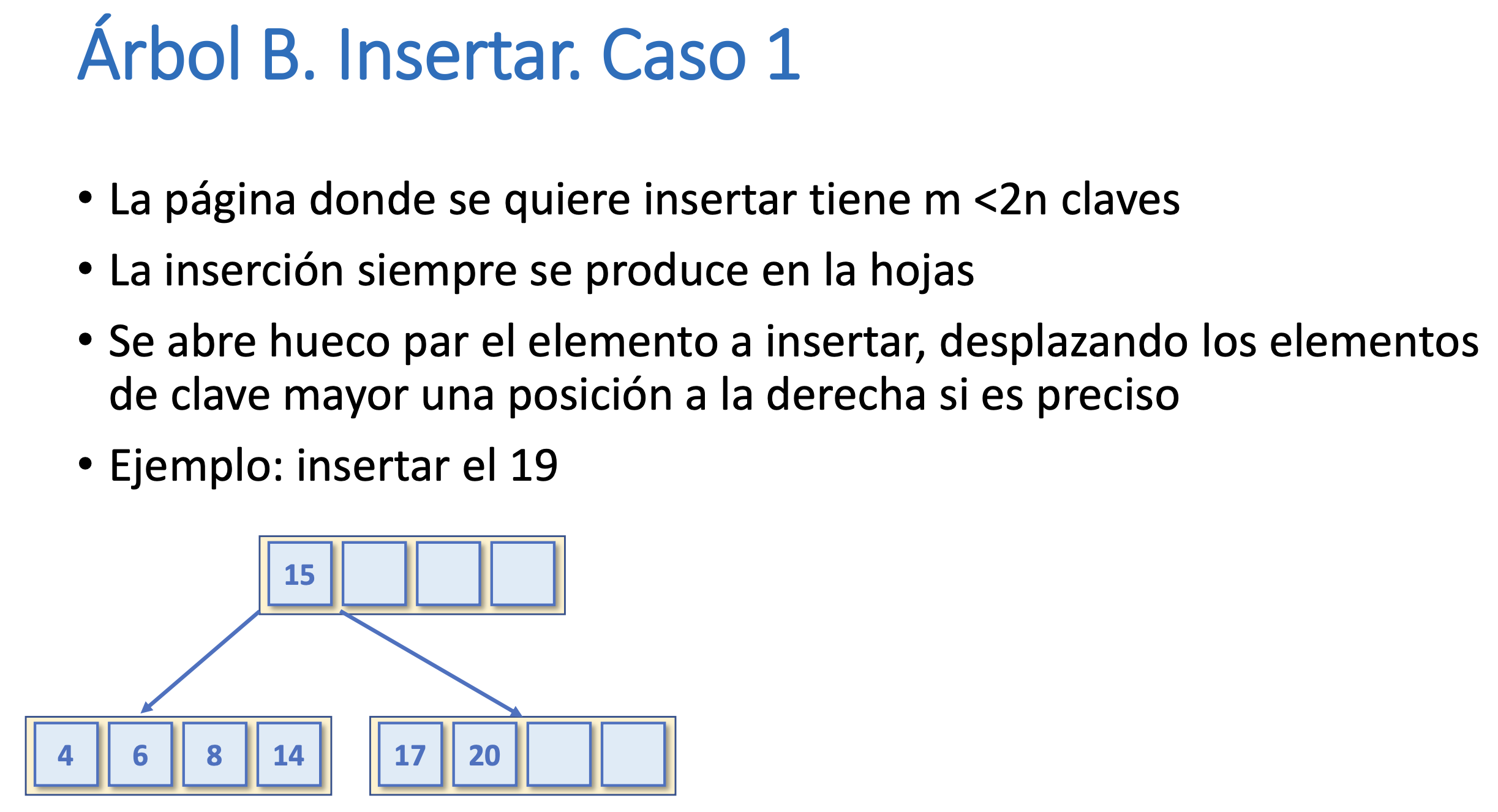
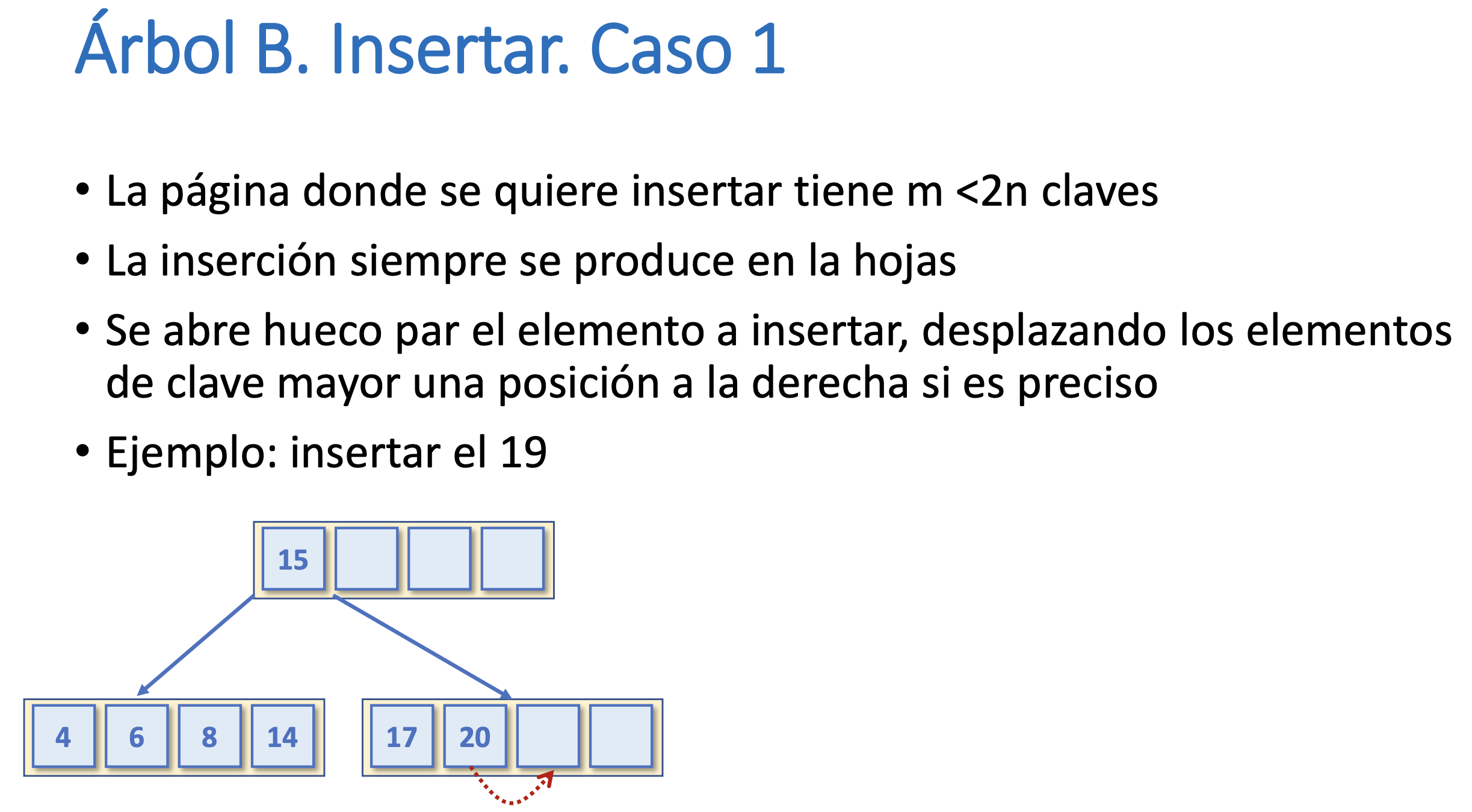
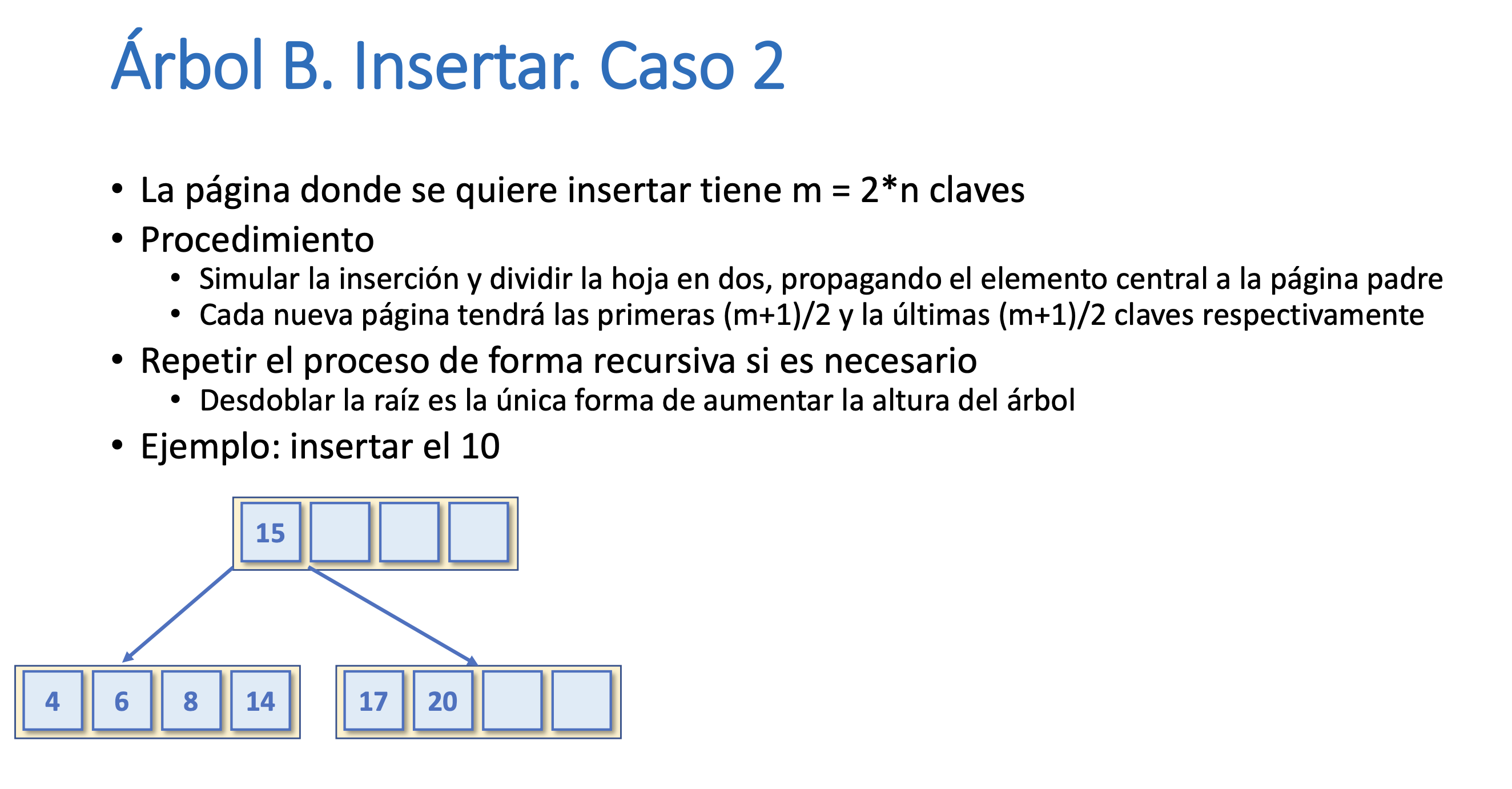
Árbol B. Insertar. Caso 2
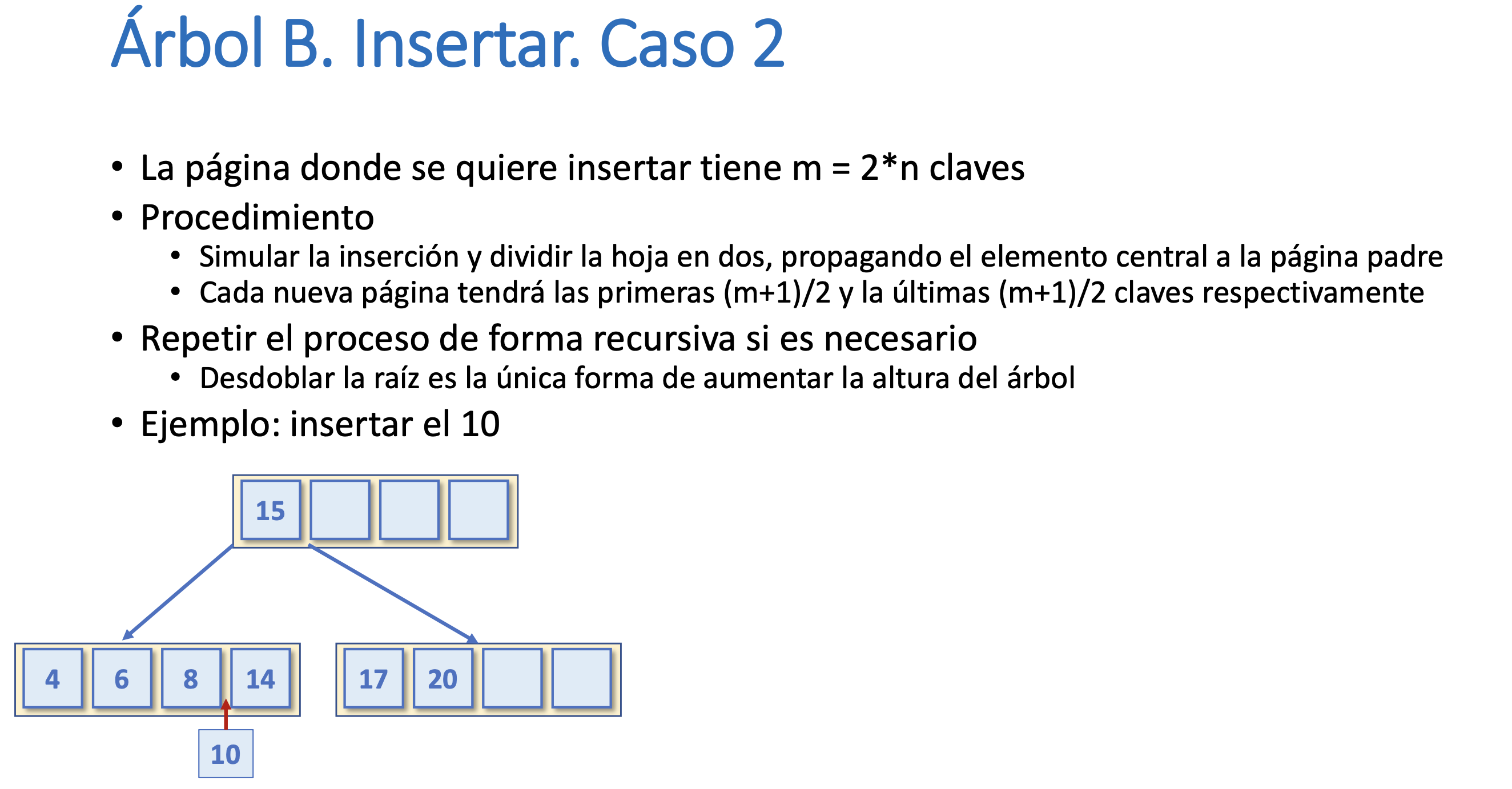
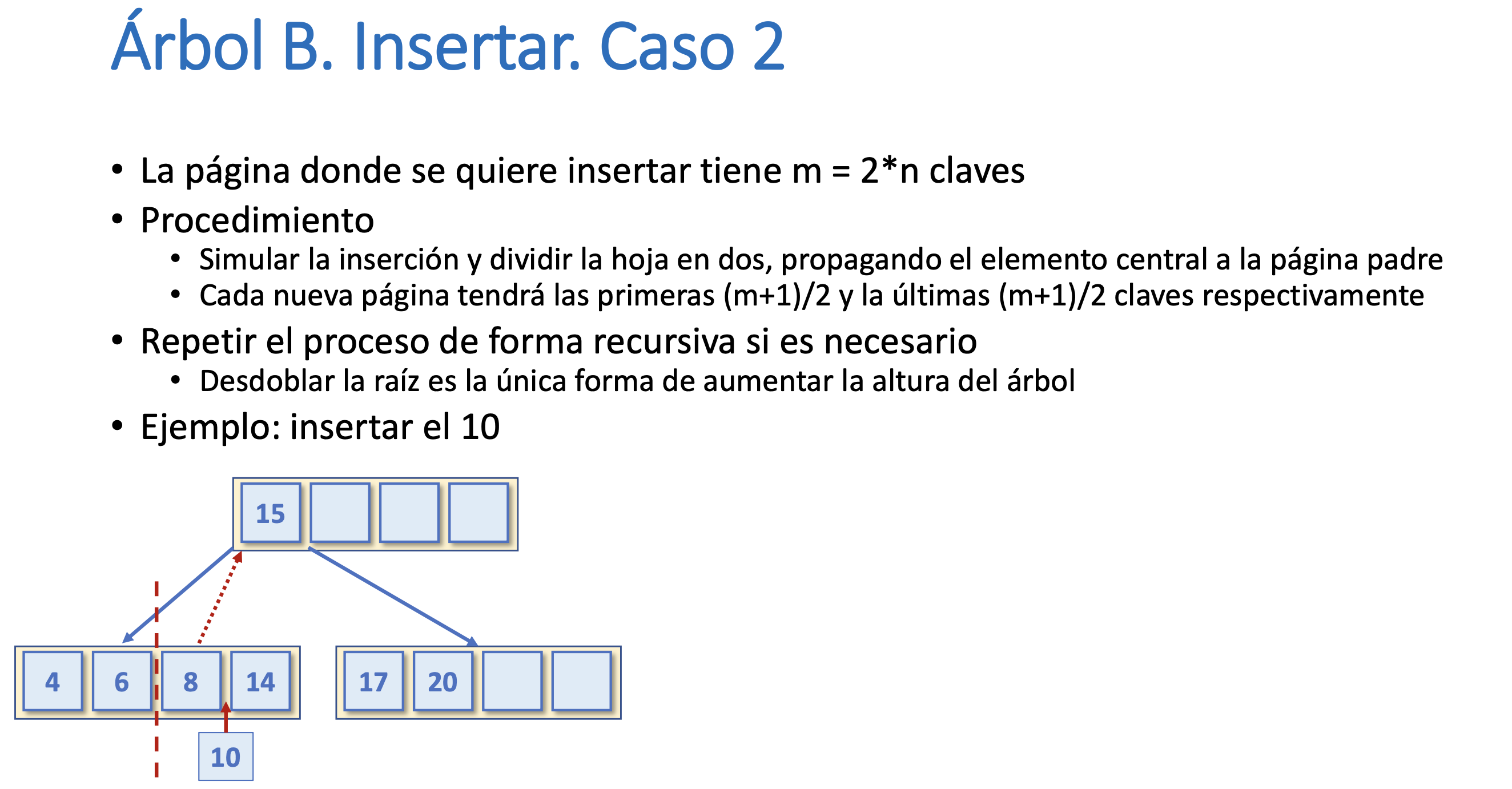
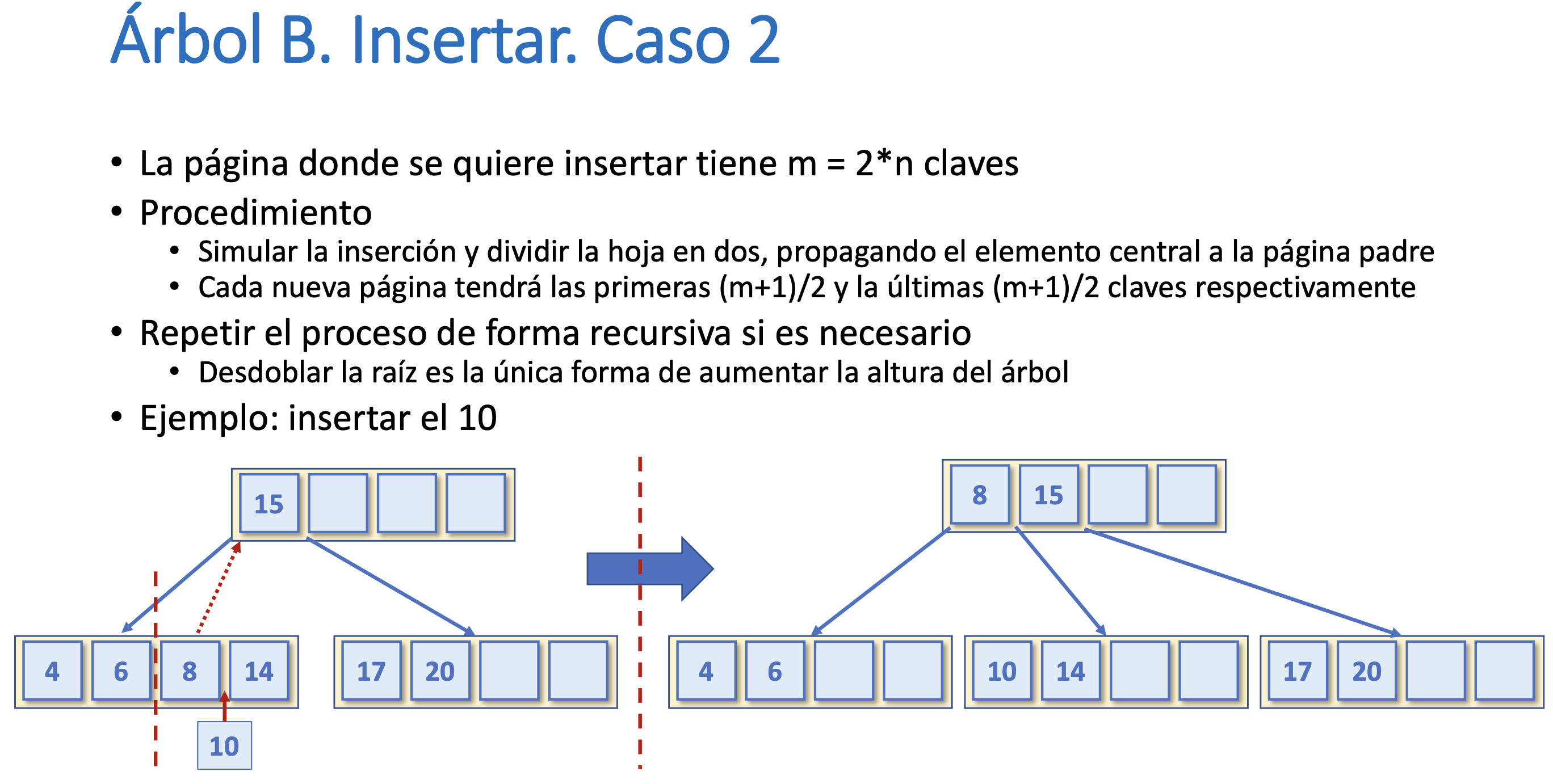
Árbol B. Insertar. Complejidad temporal

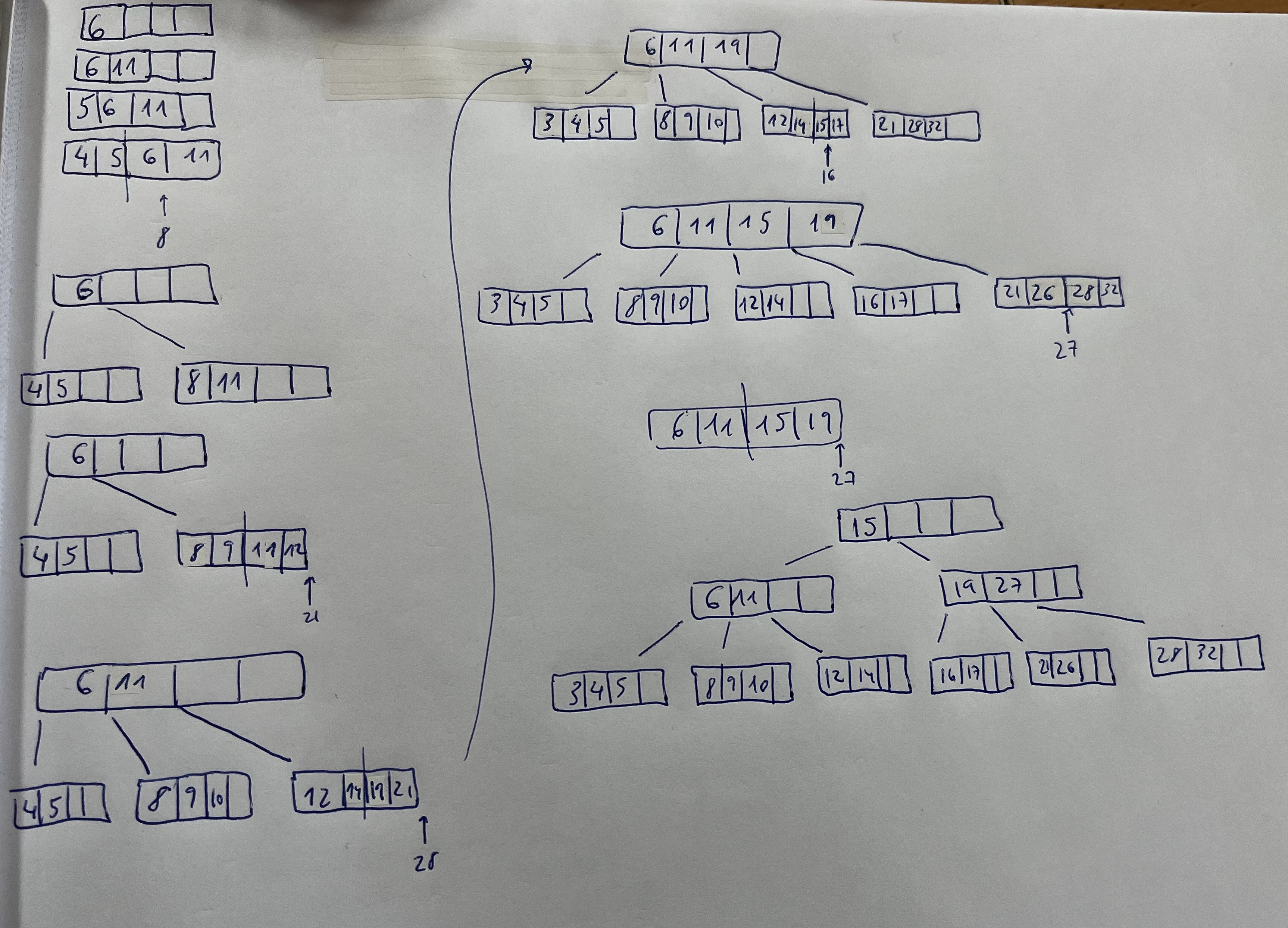
Árbol B. Ejercicios de Insertar

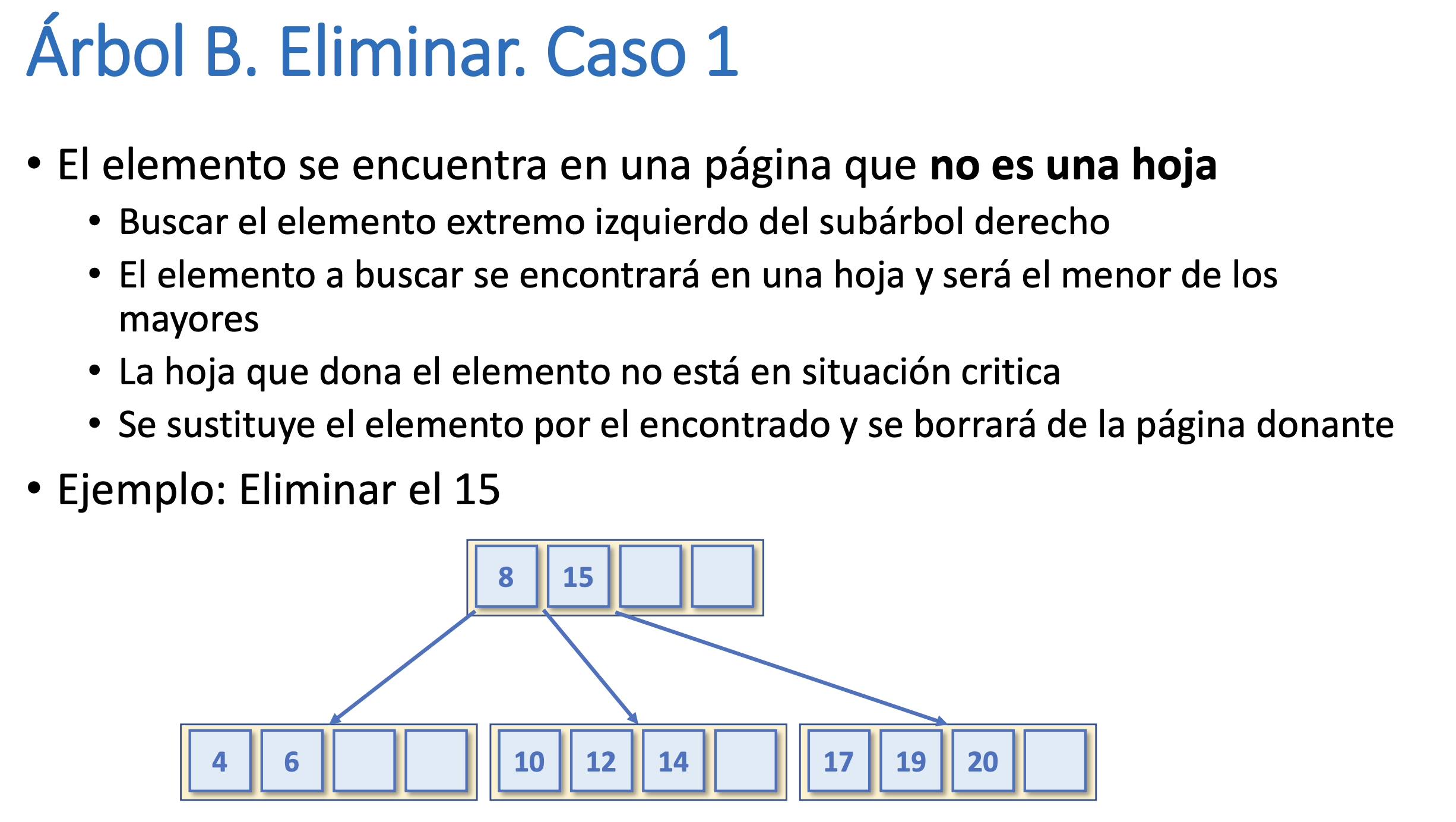
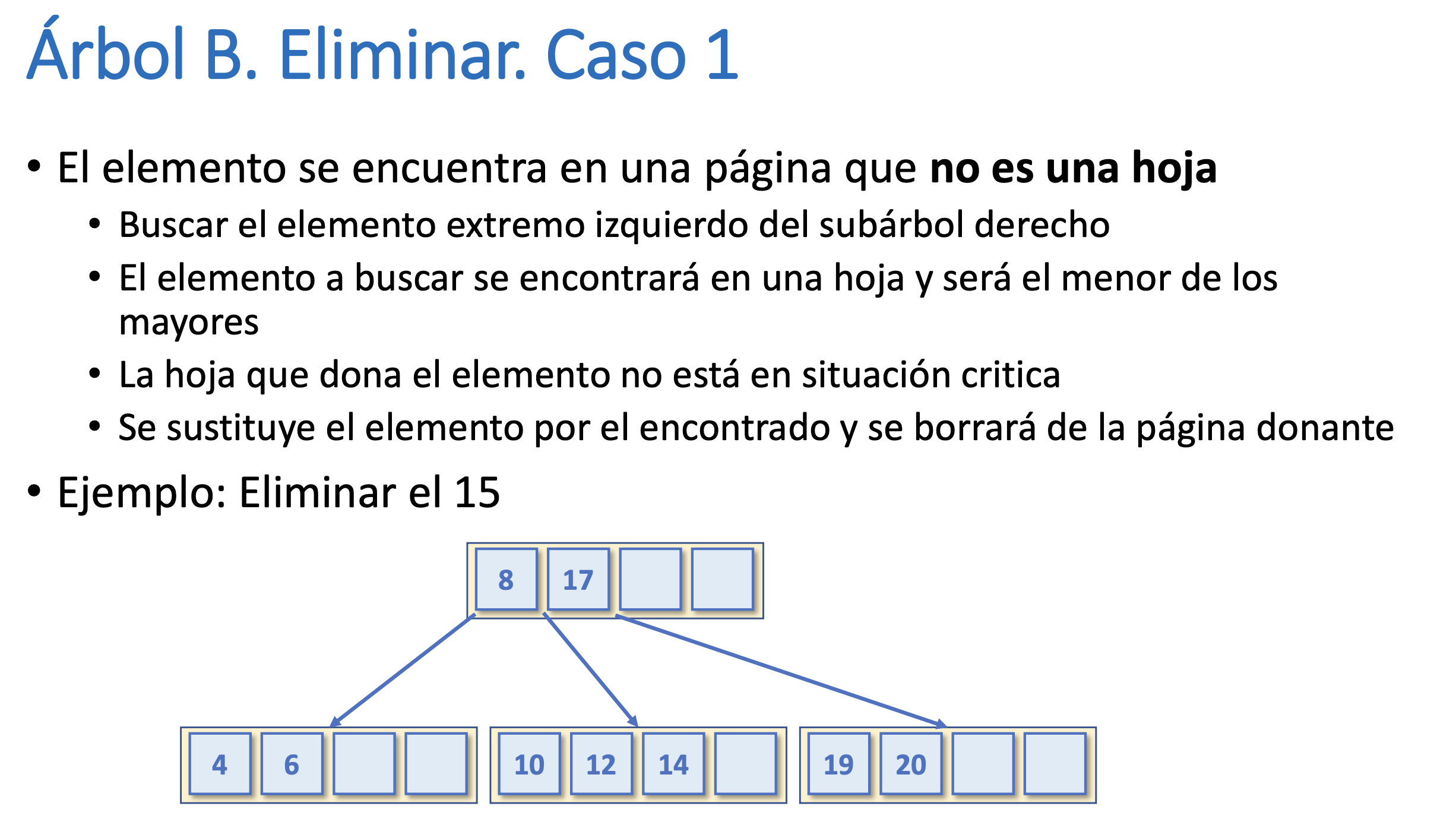
Árbol B. Eliminar. Caso 1
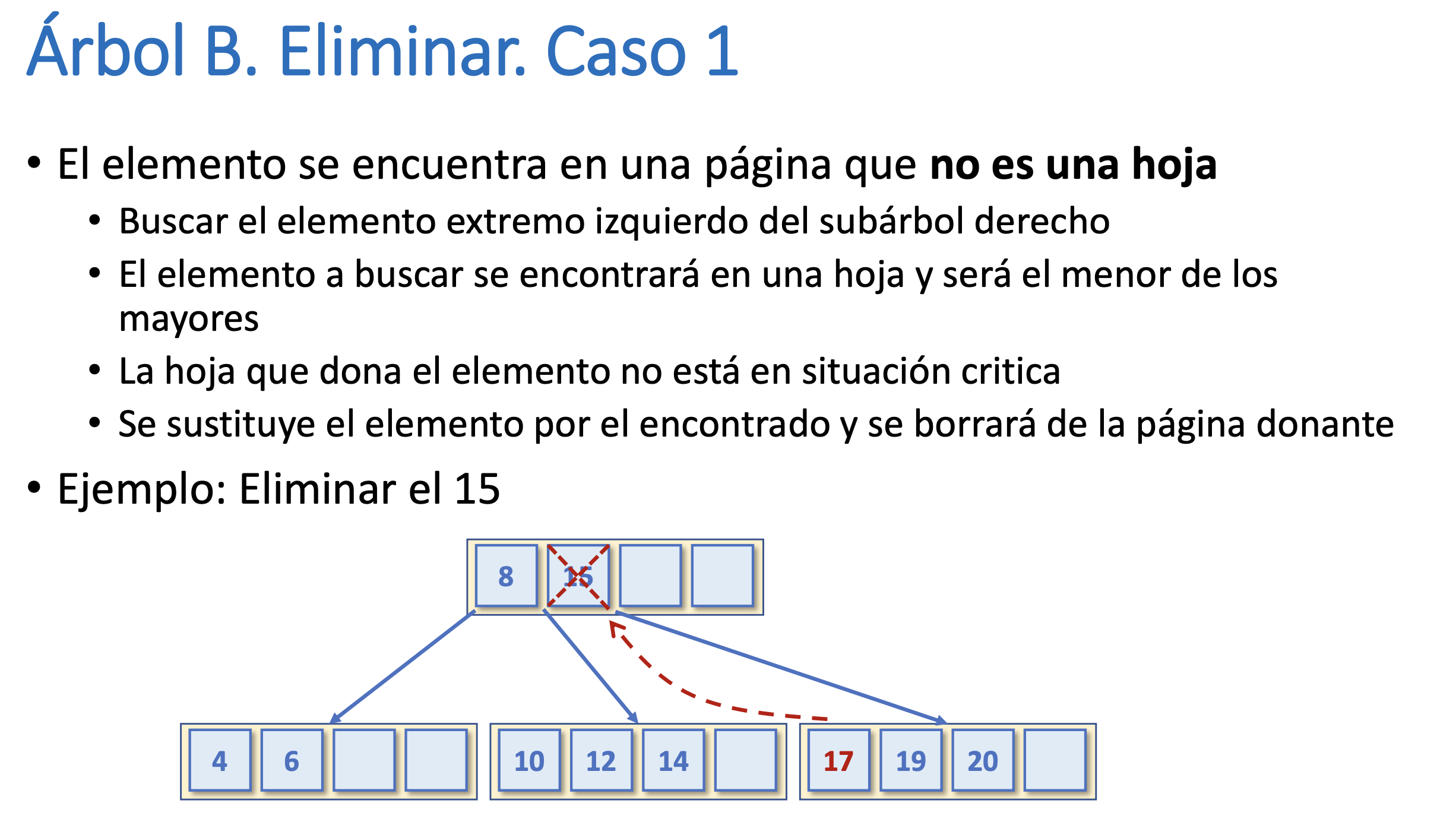
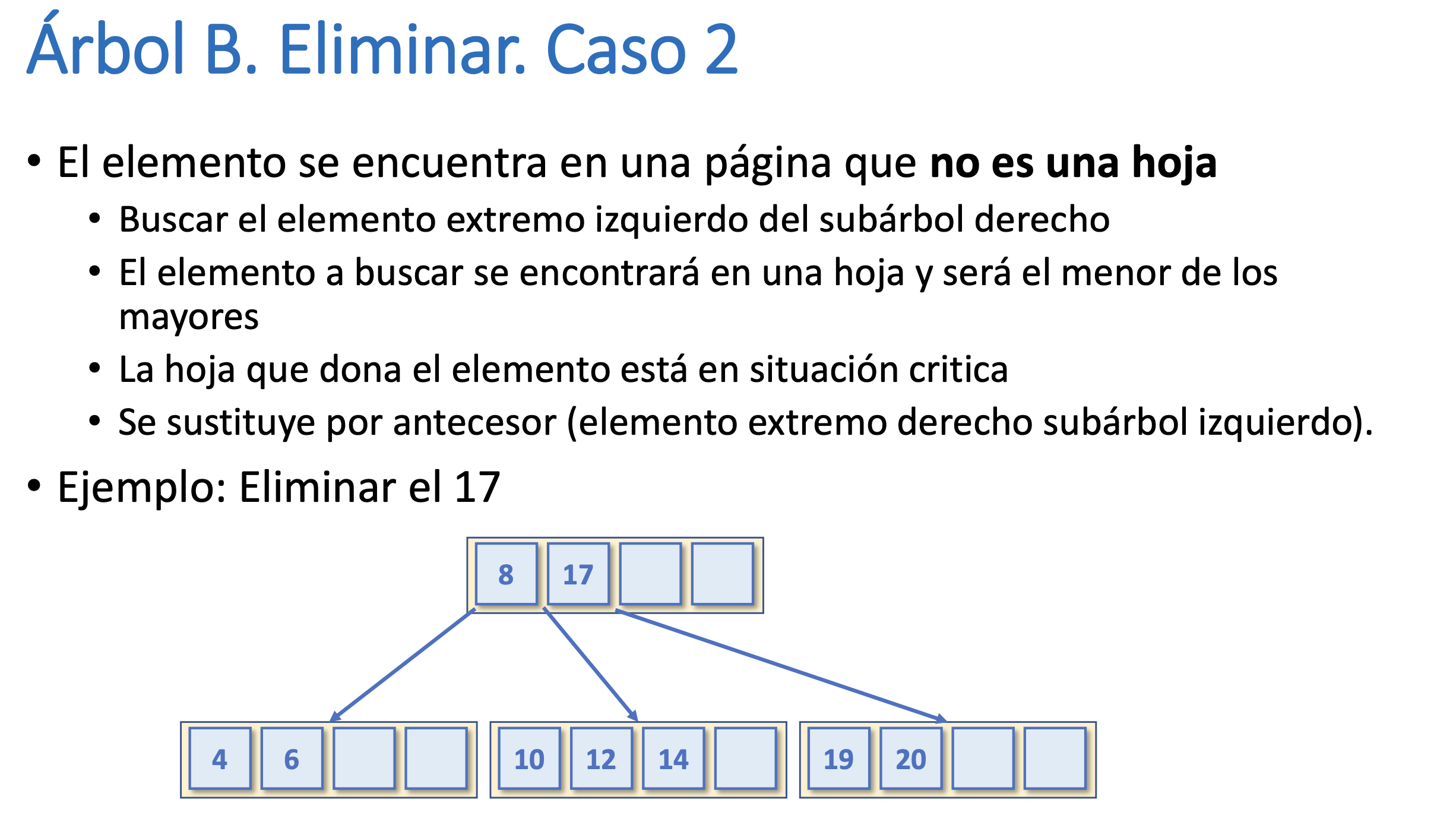
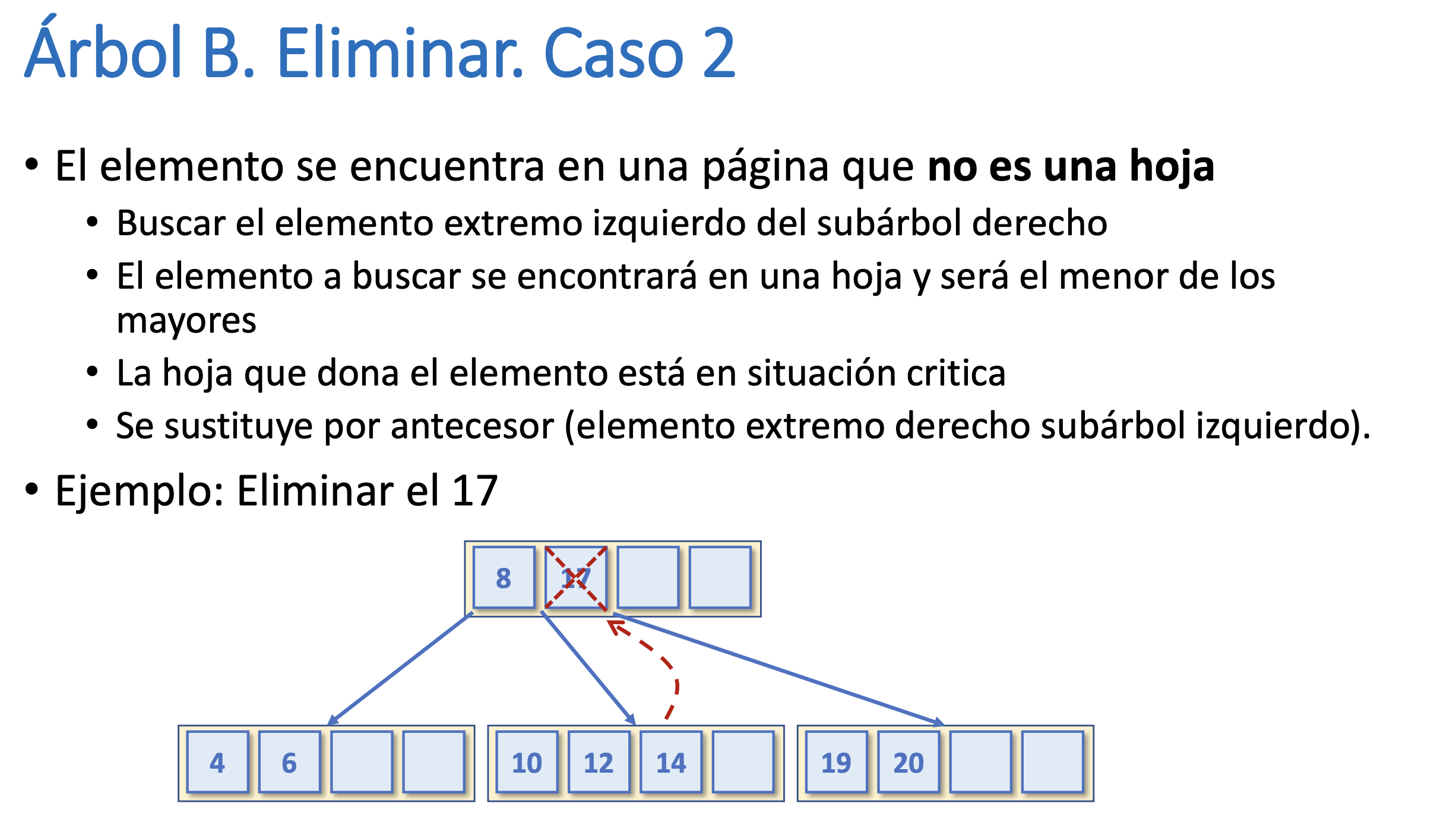
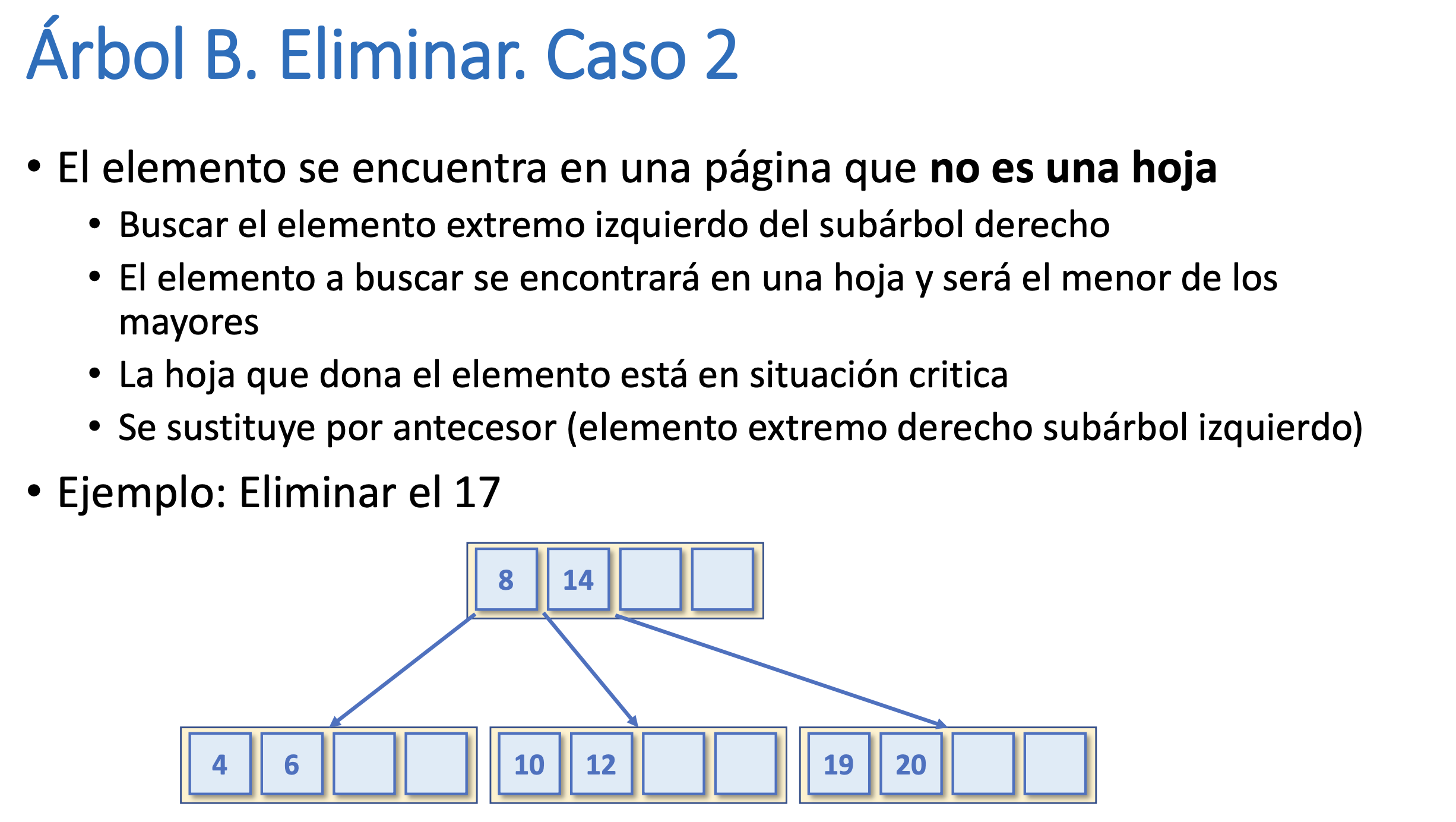
Árbol B. Eliminar. Caso 2
Árbol B. Eliminar. Caso 3
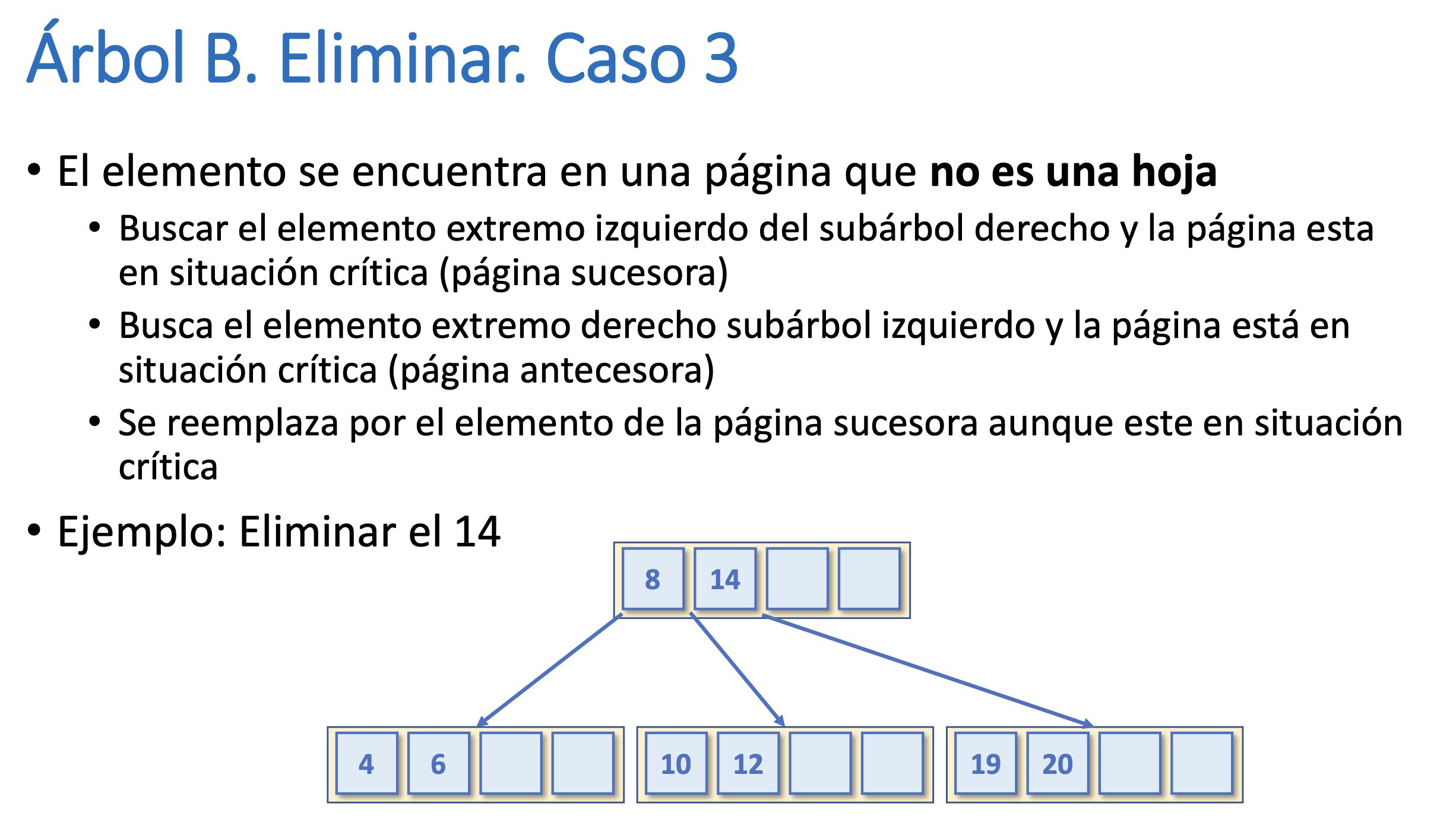
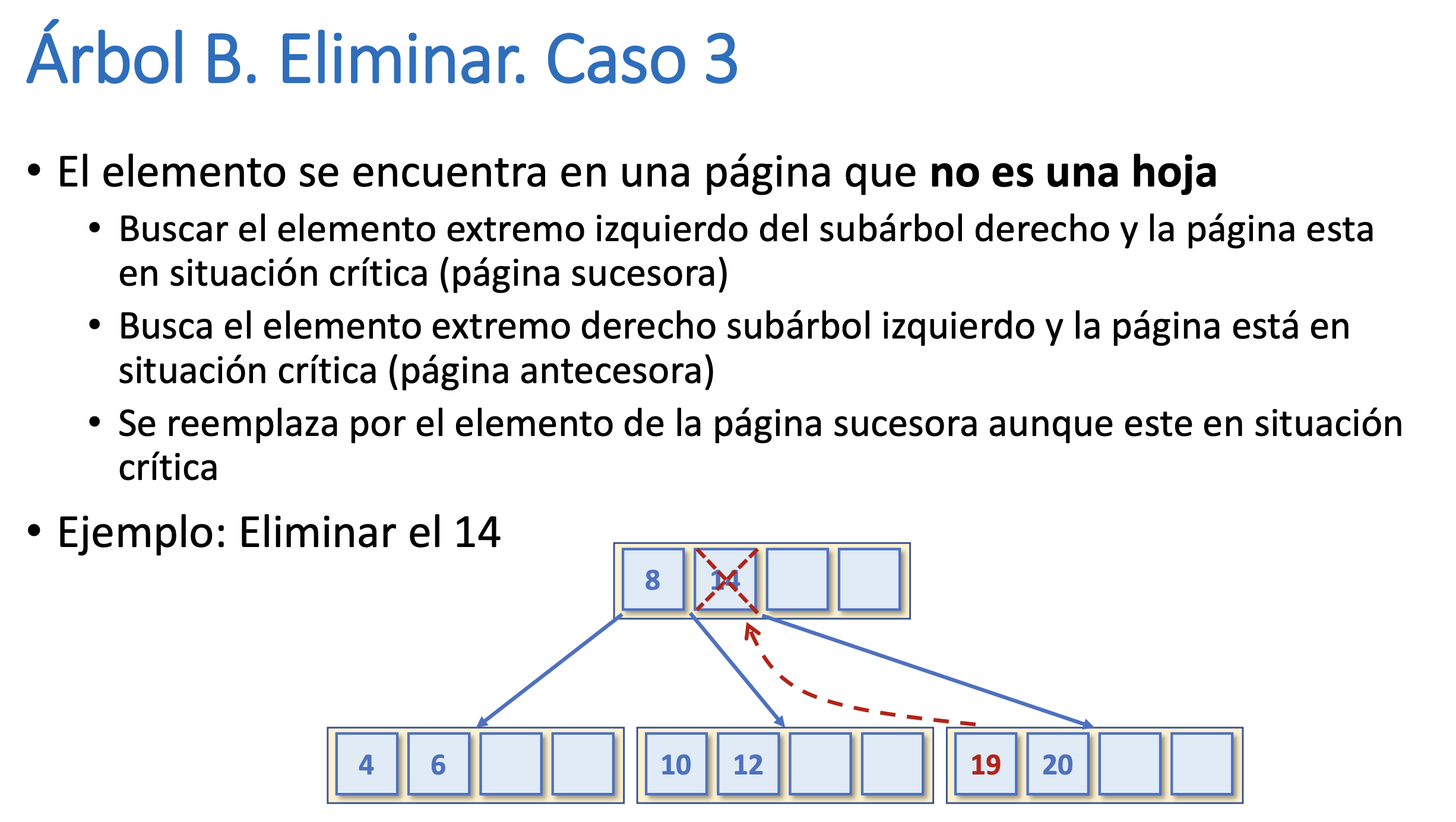
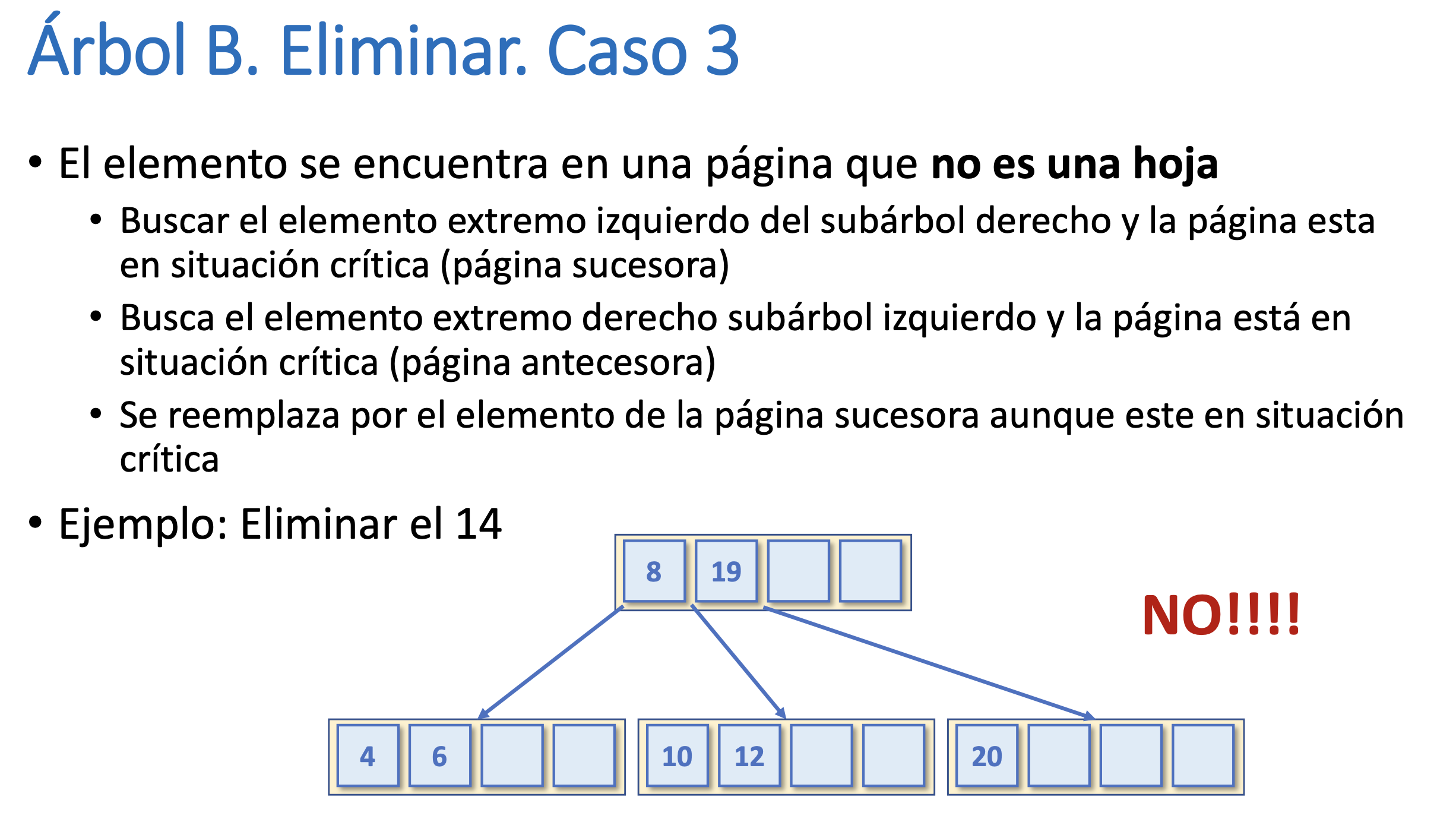
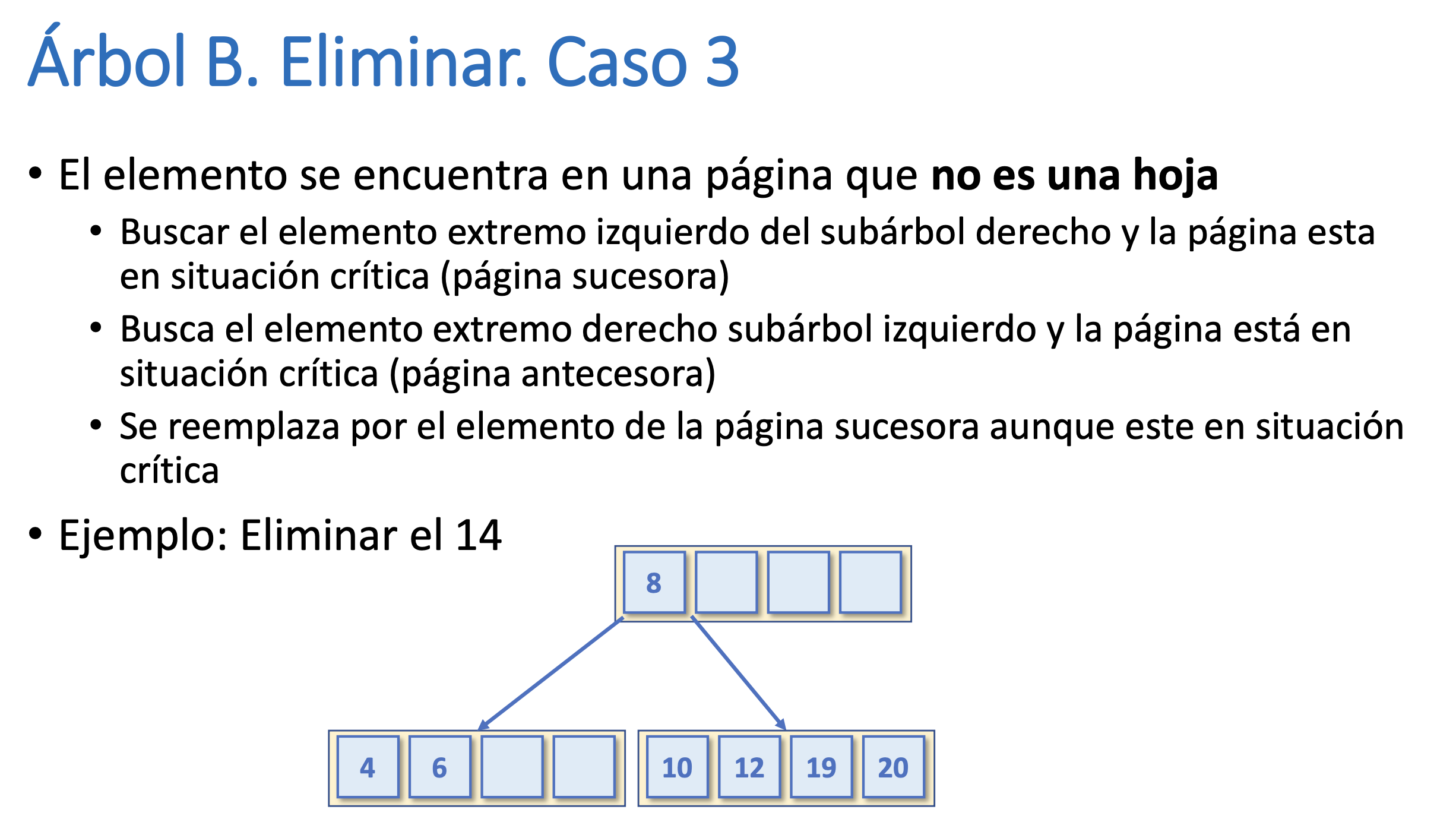
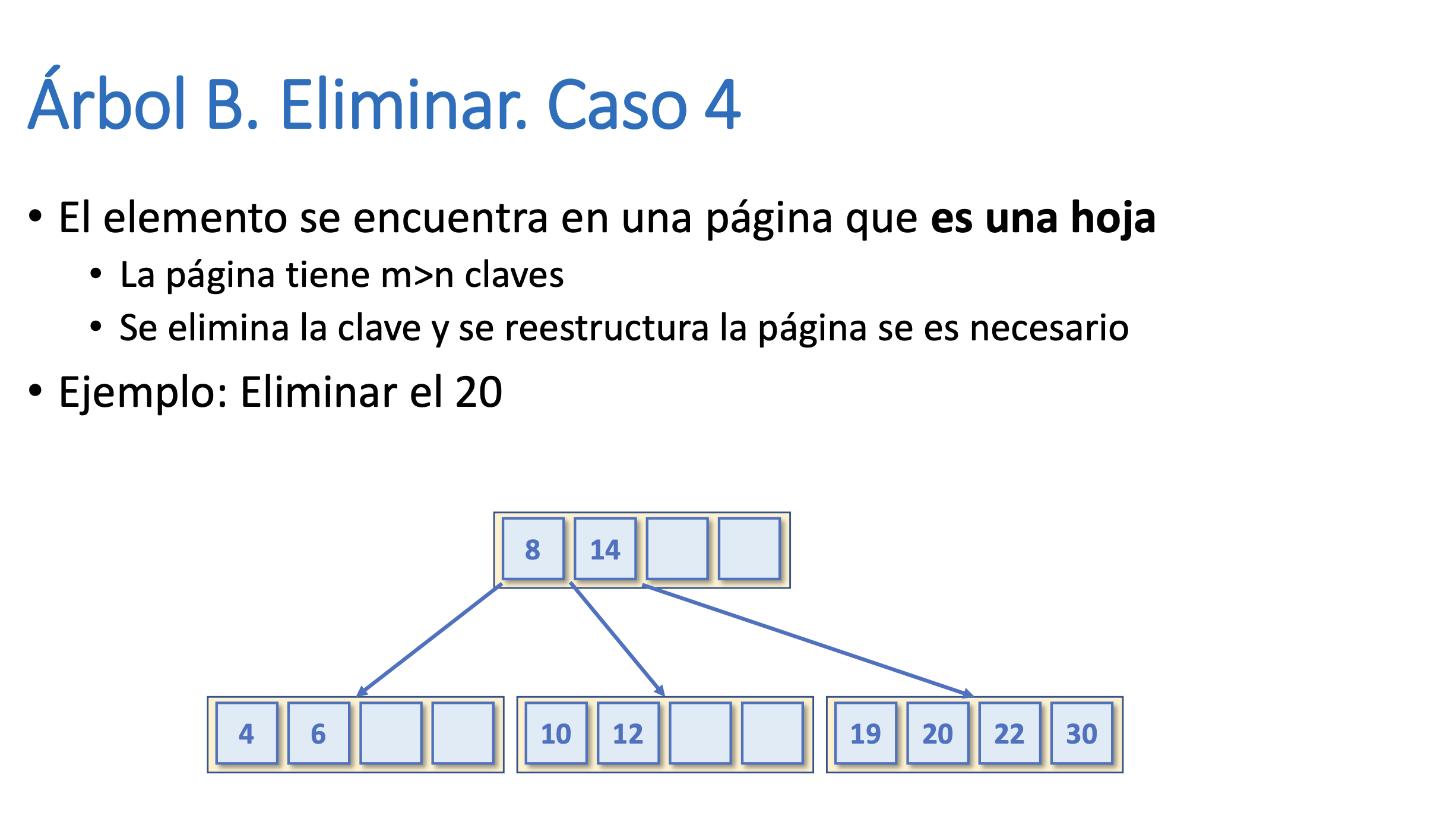
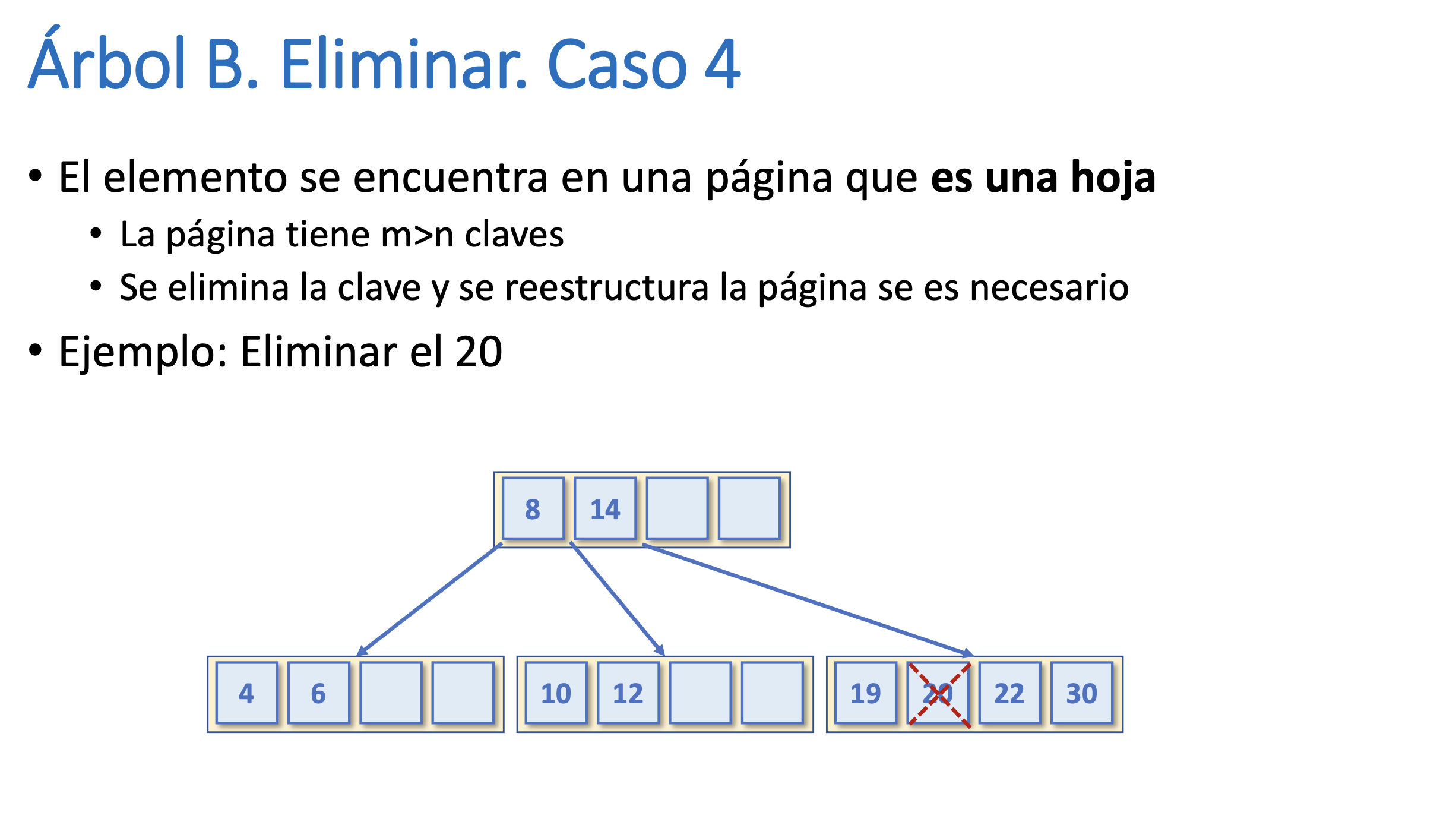
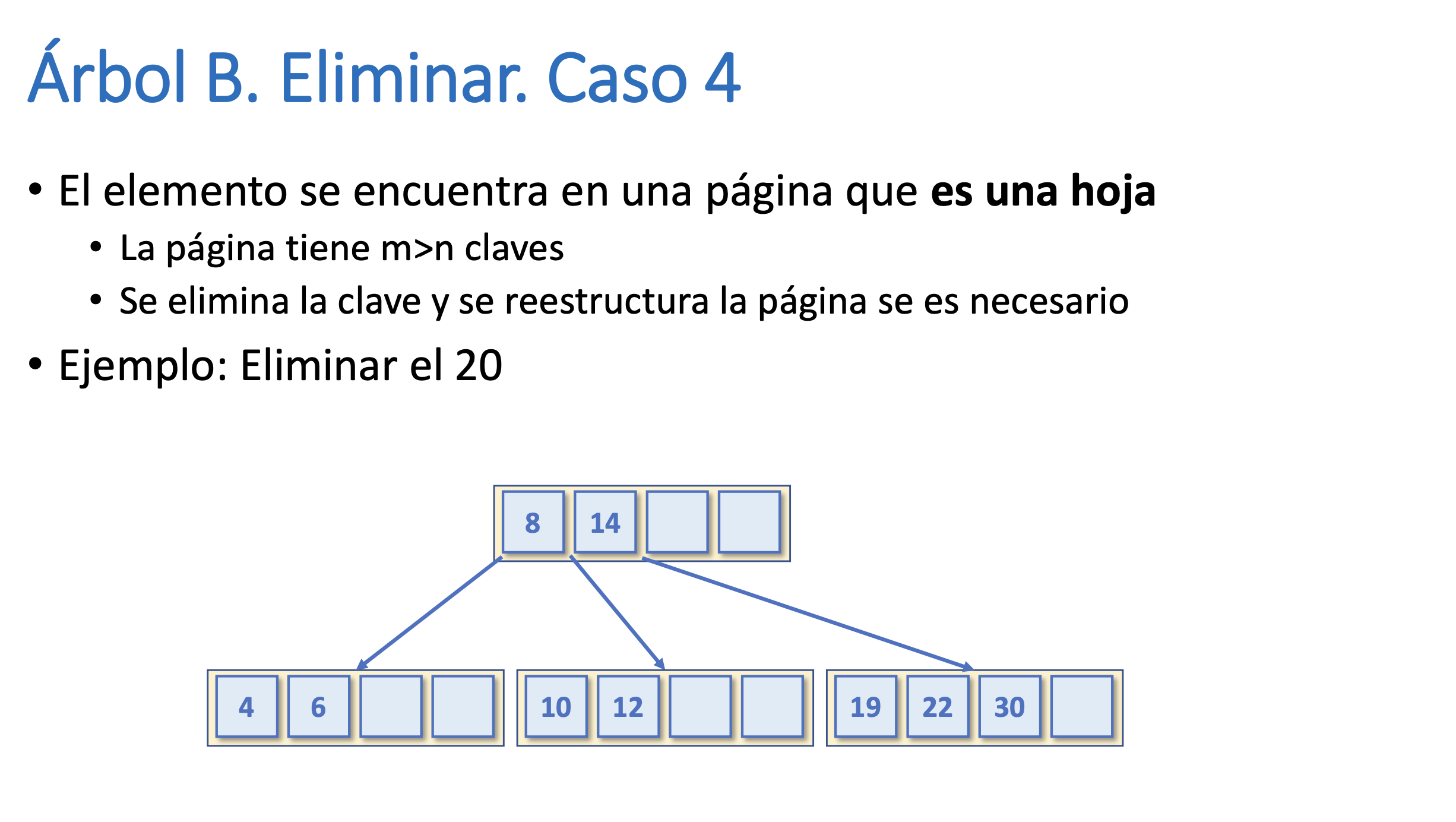
Árbol B. Eliminar. Caso 4
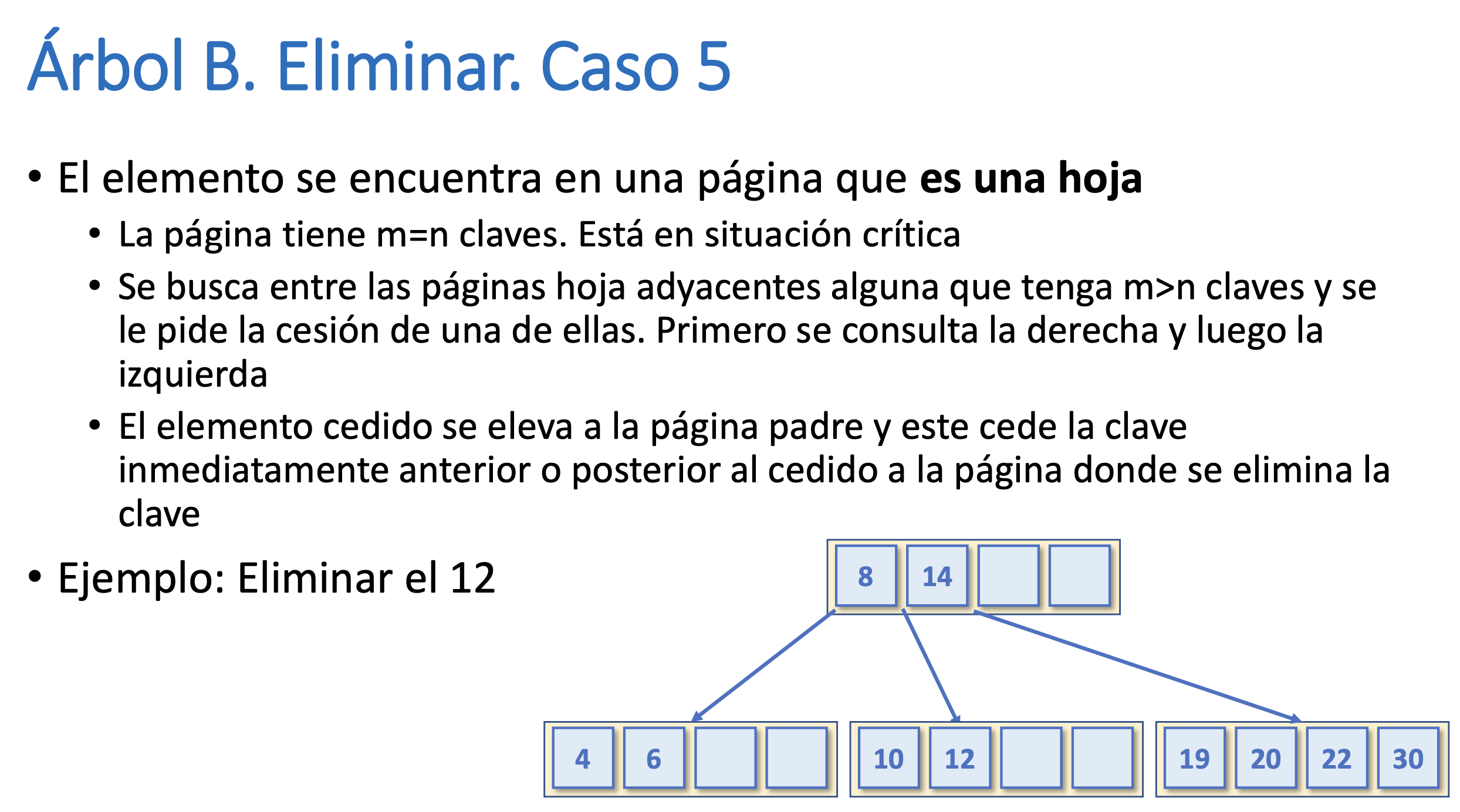
Árbol B. Eliminar. Caso 5
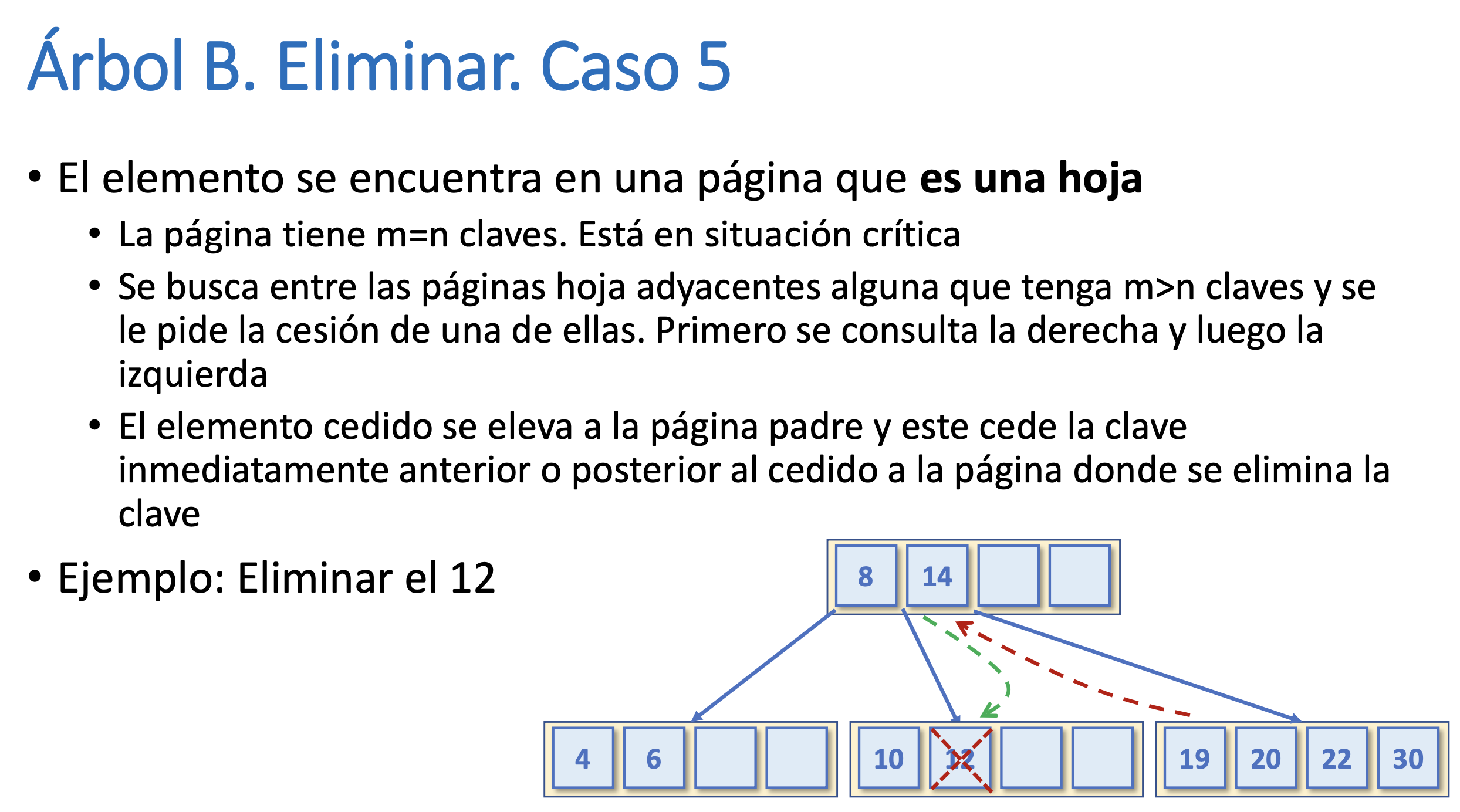
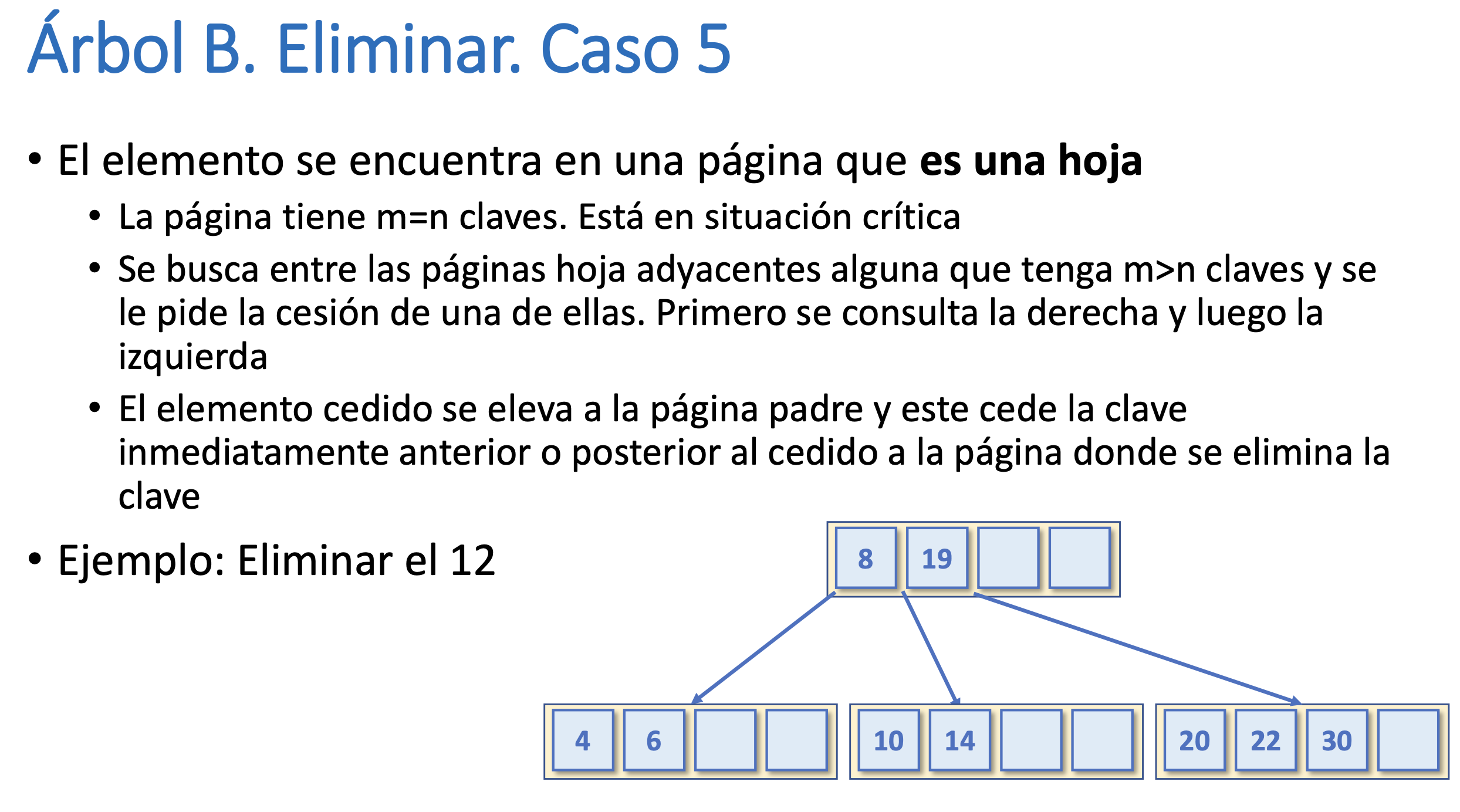
Árbol B. Eliminar. Caso 6

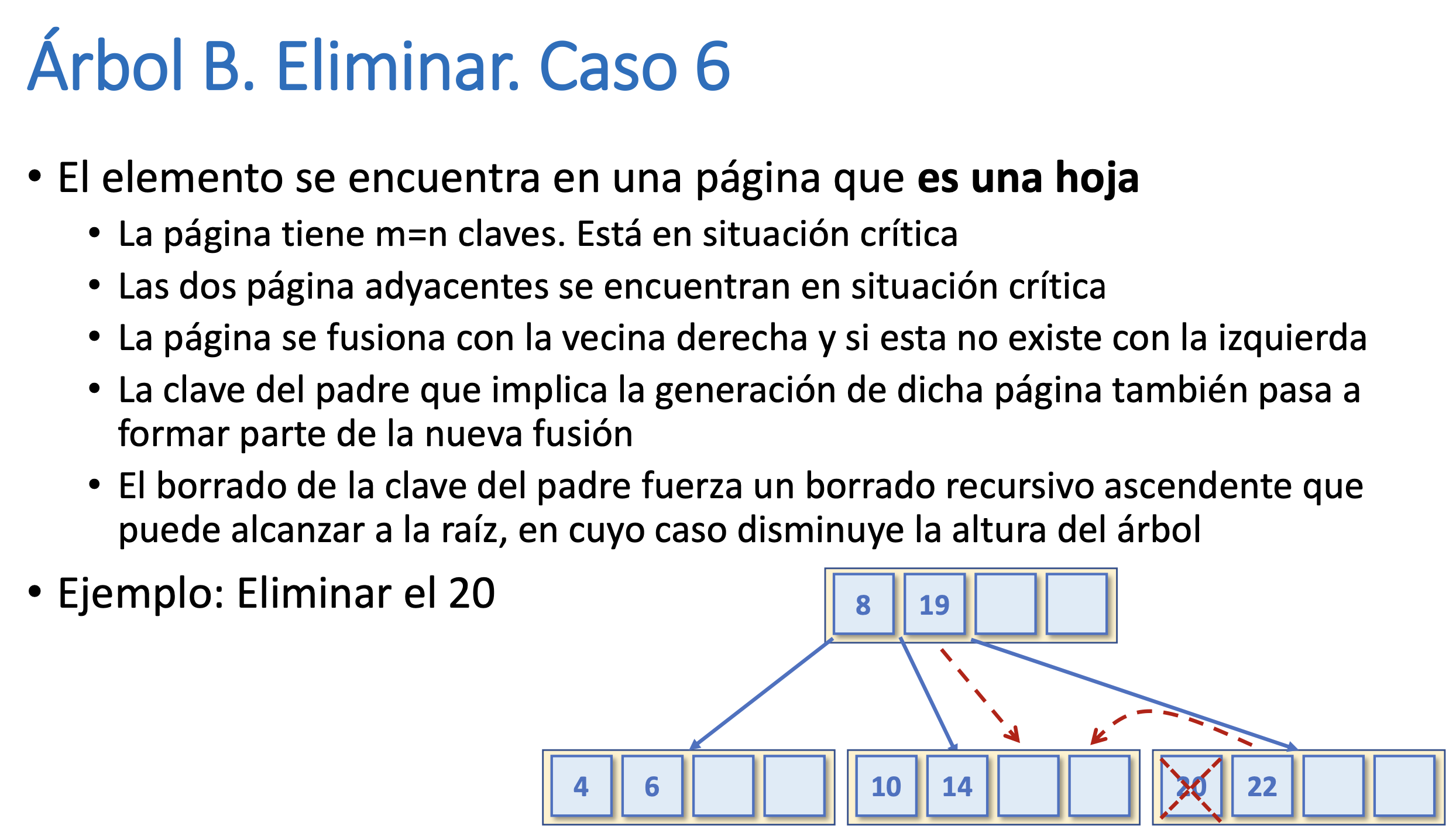
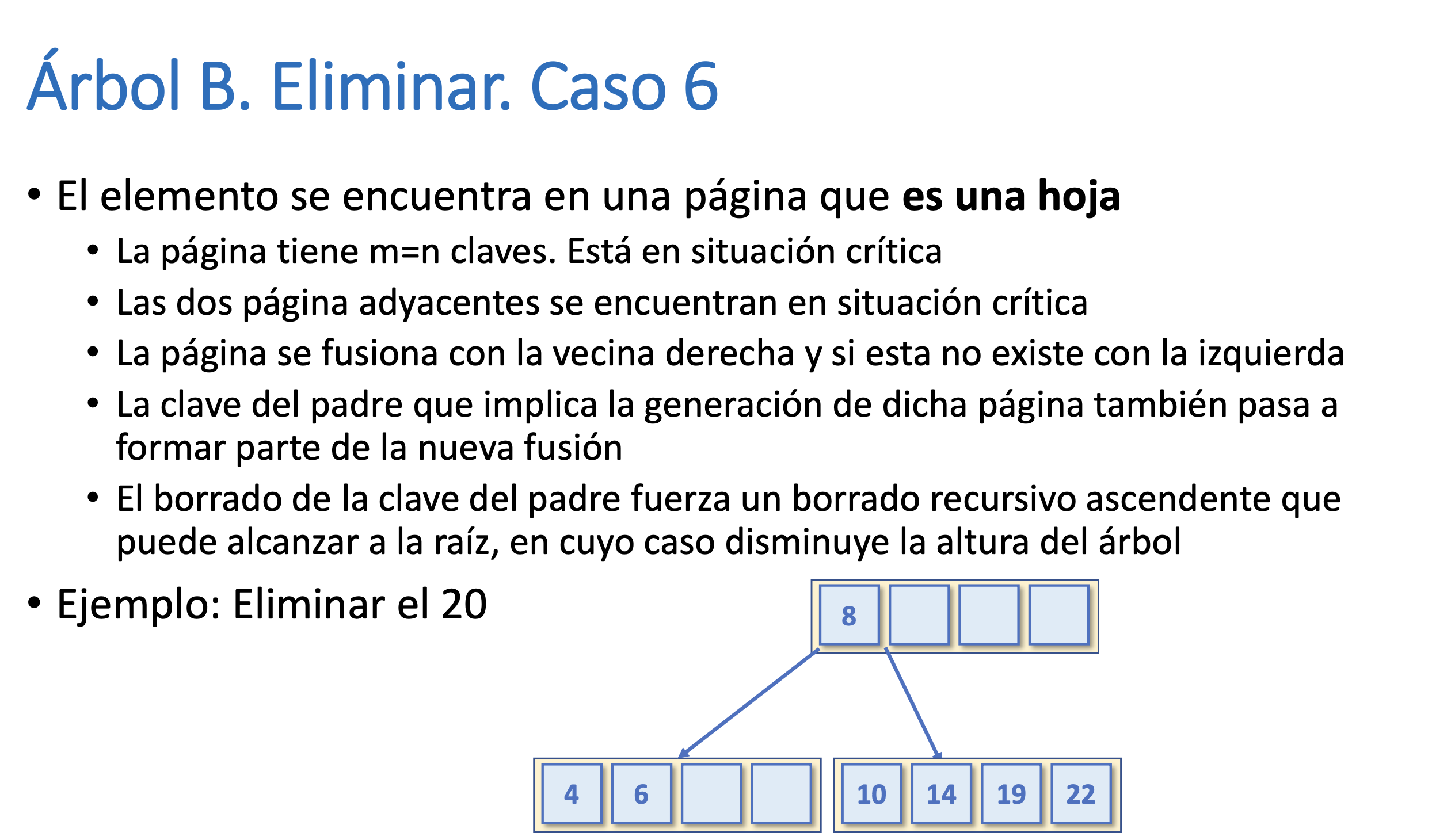
Árbol B. Eliminar. Complejidad temporal

Árbol B. Ejercicios Eliminar