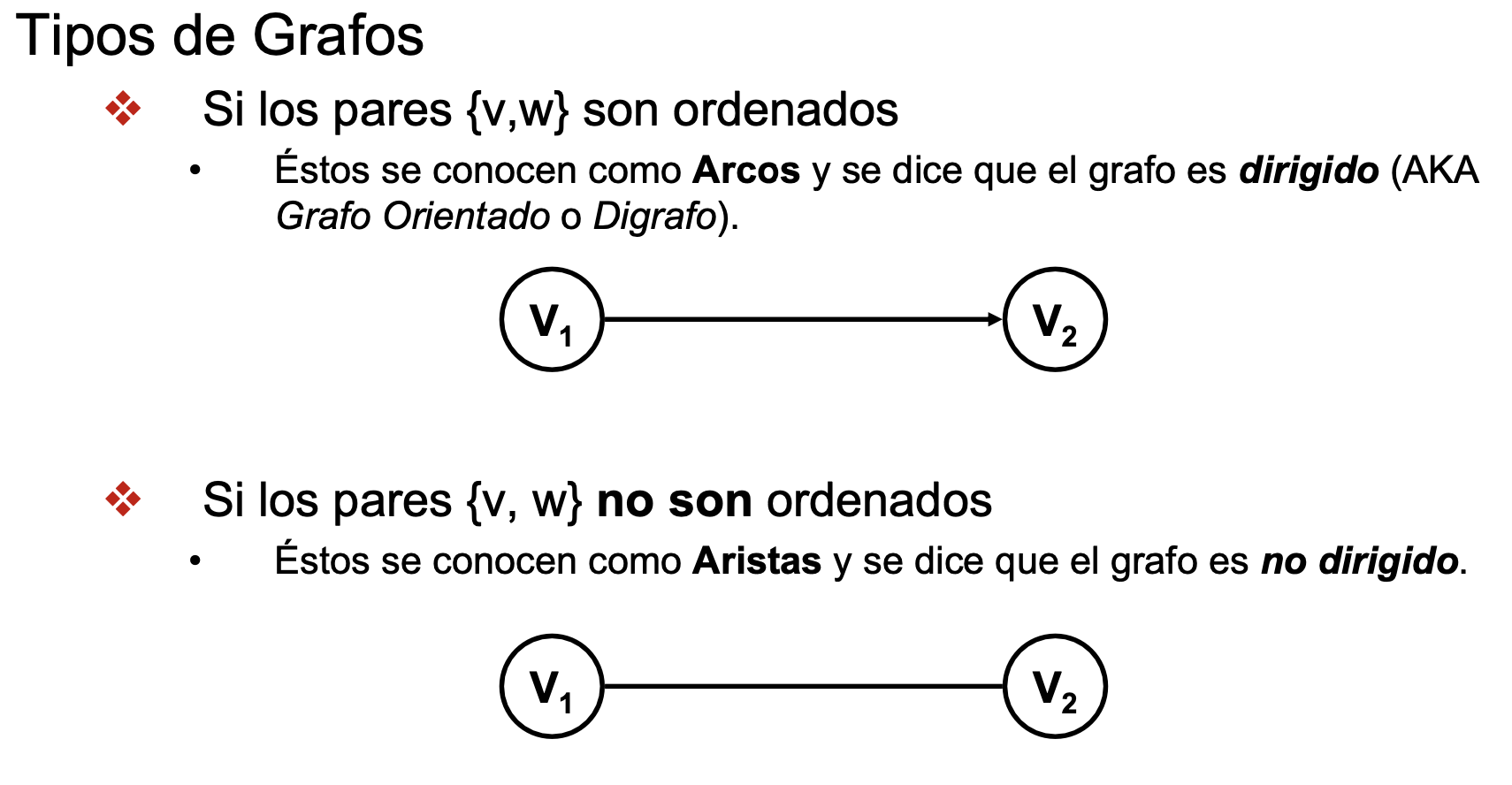
- Arista: relación entre nodos en la que existe un orden (grafo dirigido: -⇒, ⇐-)
- Arco: relación entre nodos en la que no existe un orden (grafo no dirigido: ---)
¿Qué es un grafo?
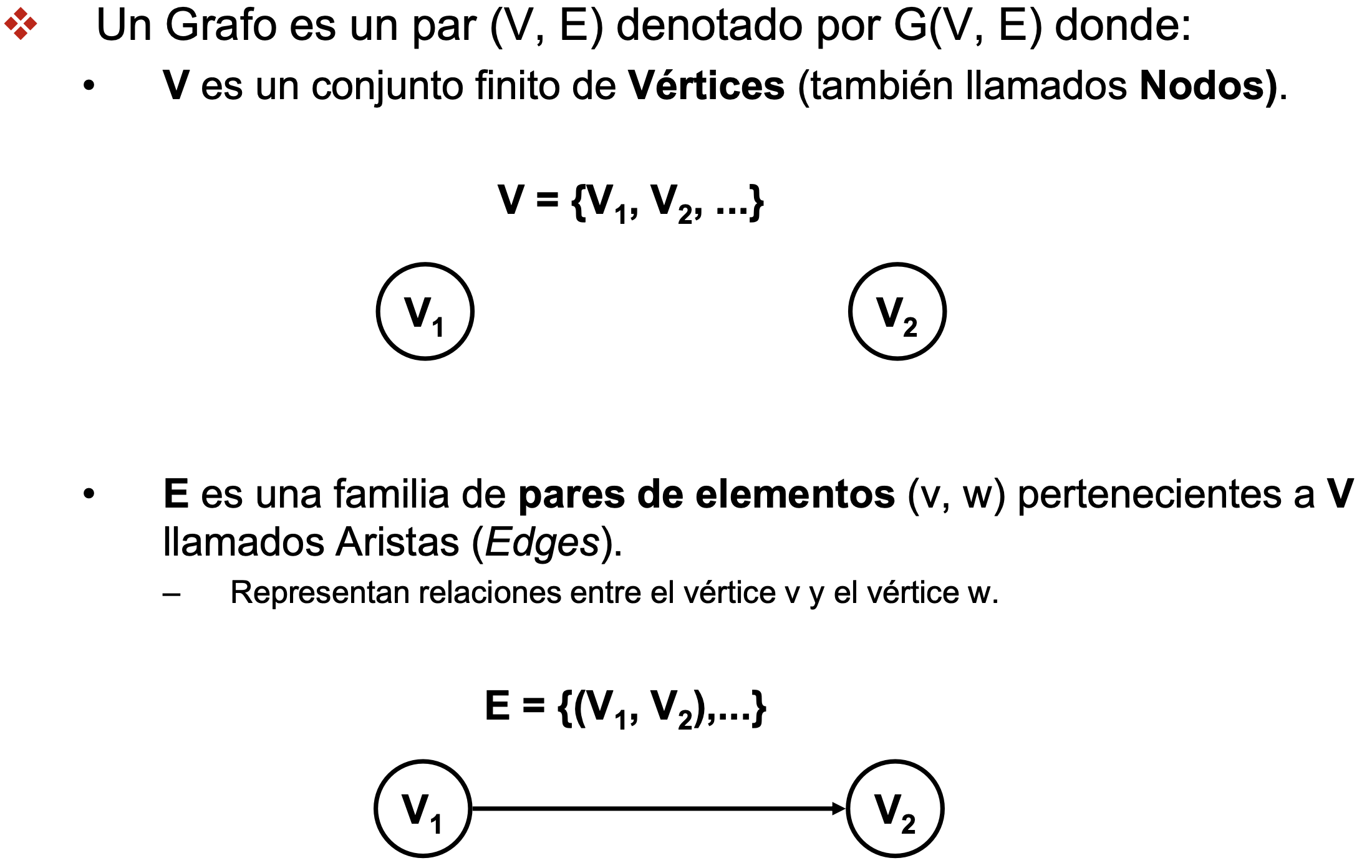
- Un grafo es un modelo matemático que permite representar relaciones arbitrarias entre objetos.
Tipos de grafos
Definición formal
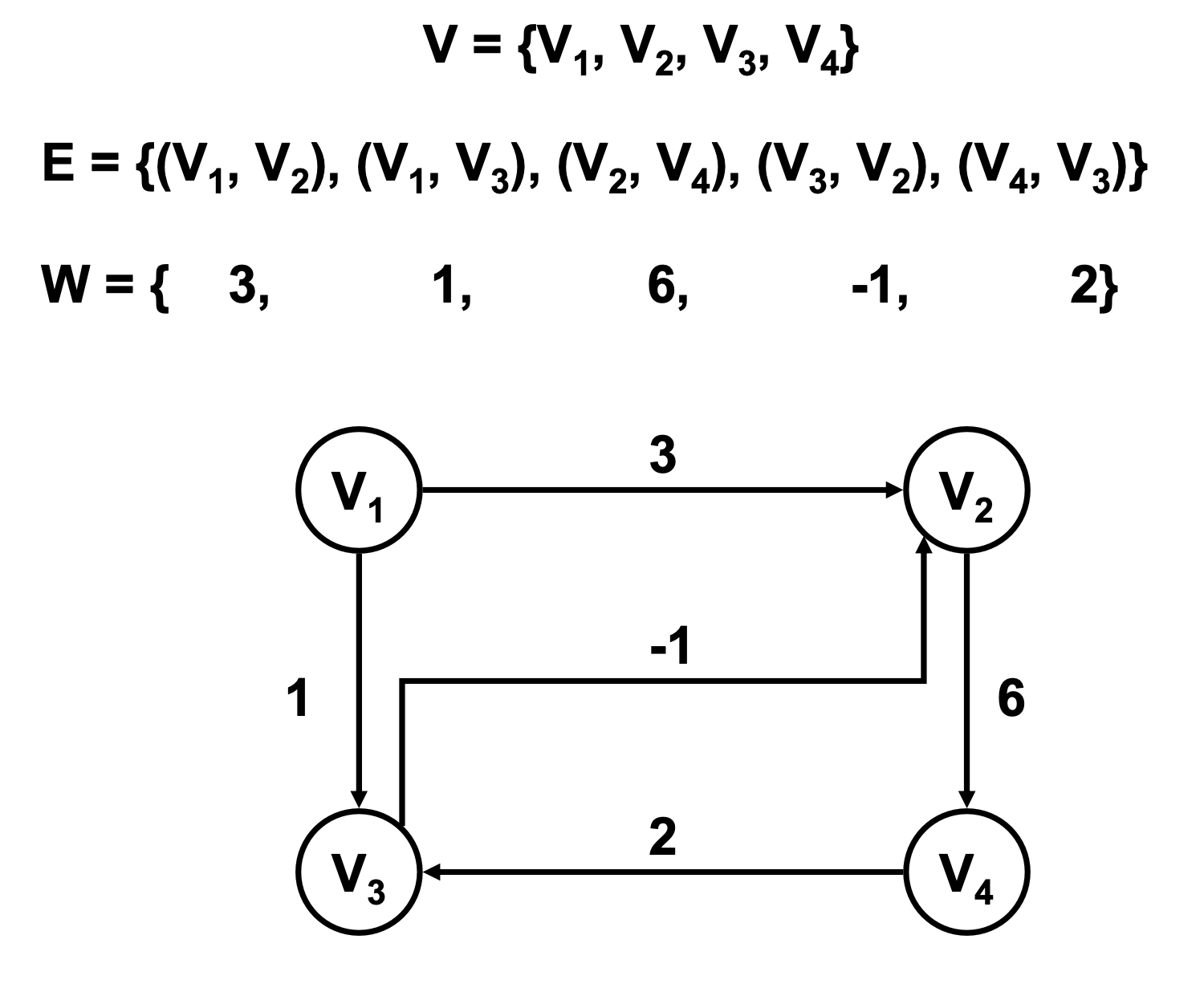
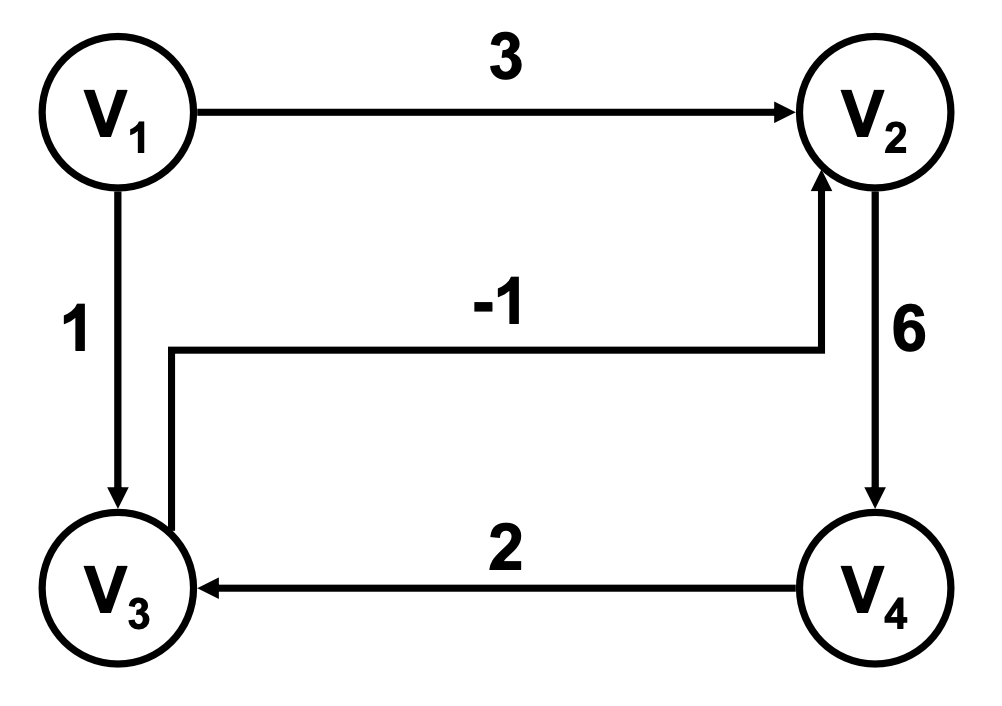
Conceptos básicos
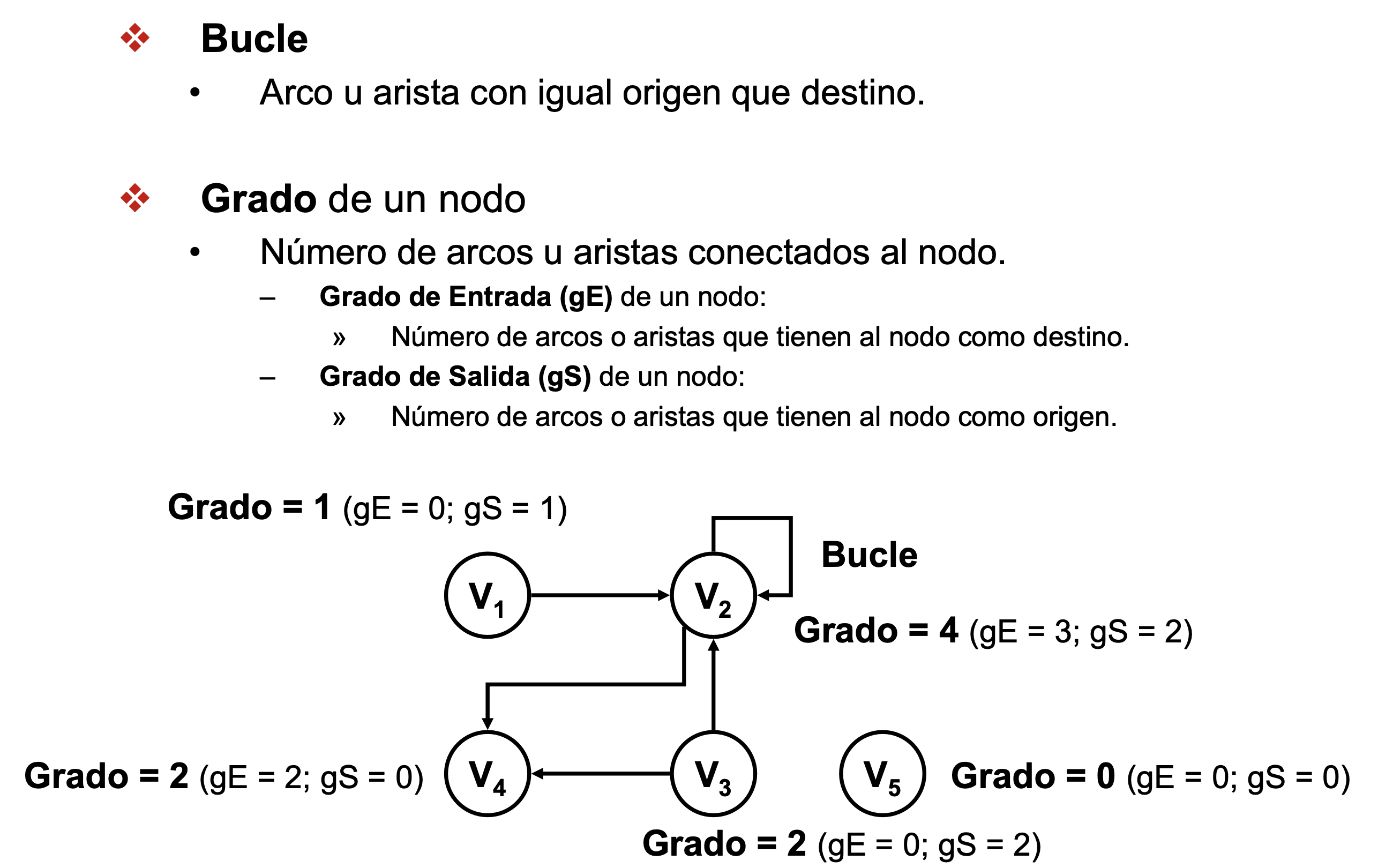
- Bucle: Arco u arista con igual origen que destino.
- Grado de un nodo: Número de arcos u aristas conectados al nodo.
- Grado de Entrada (gE) de un nodo: Número de arcos o aristas que tienen al nodo como destino
- Grado de Salida (gS) de un nodo: Número de arcos o aristas que tienen al nodo como origen.
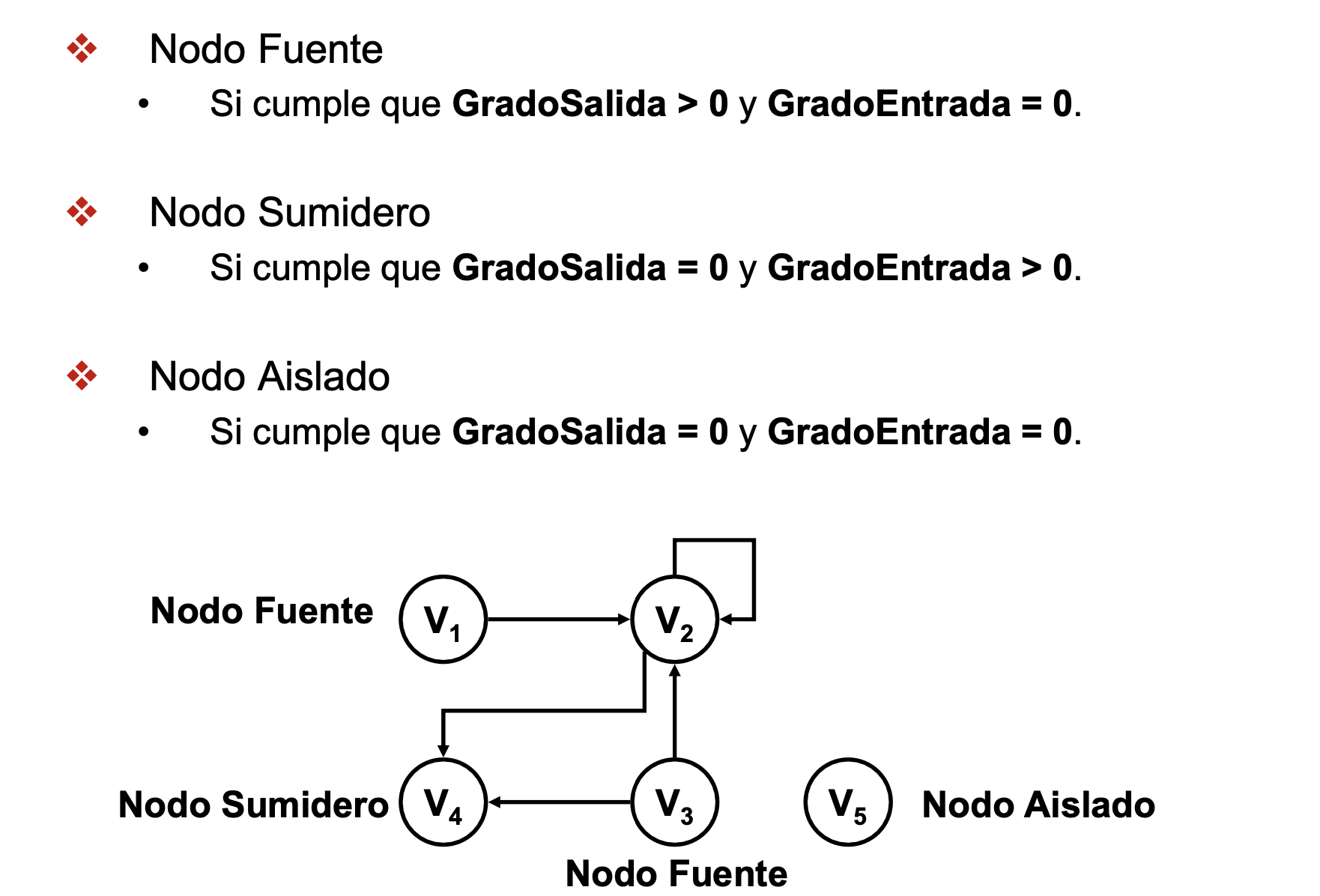
- V3 es un nodo fuente (nodo que se conecta con todo el mundo)
- V4 es un nodo sumidero (nodo que no se conecta con nadie pero que es accesible para todo el mundo)
- V5 es u nodo aislado (ningún grado de entrada ni ninguno de salida)
Capacidad de un grafo
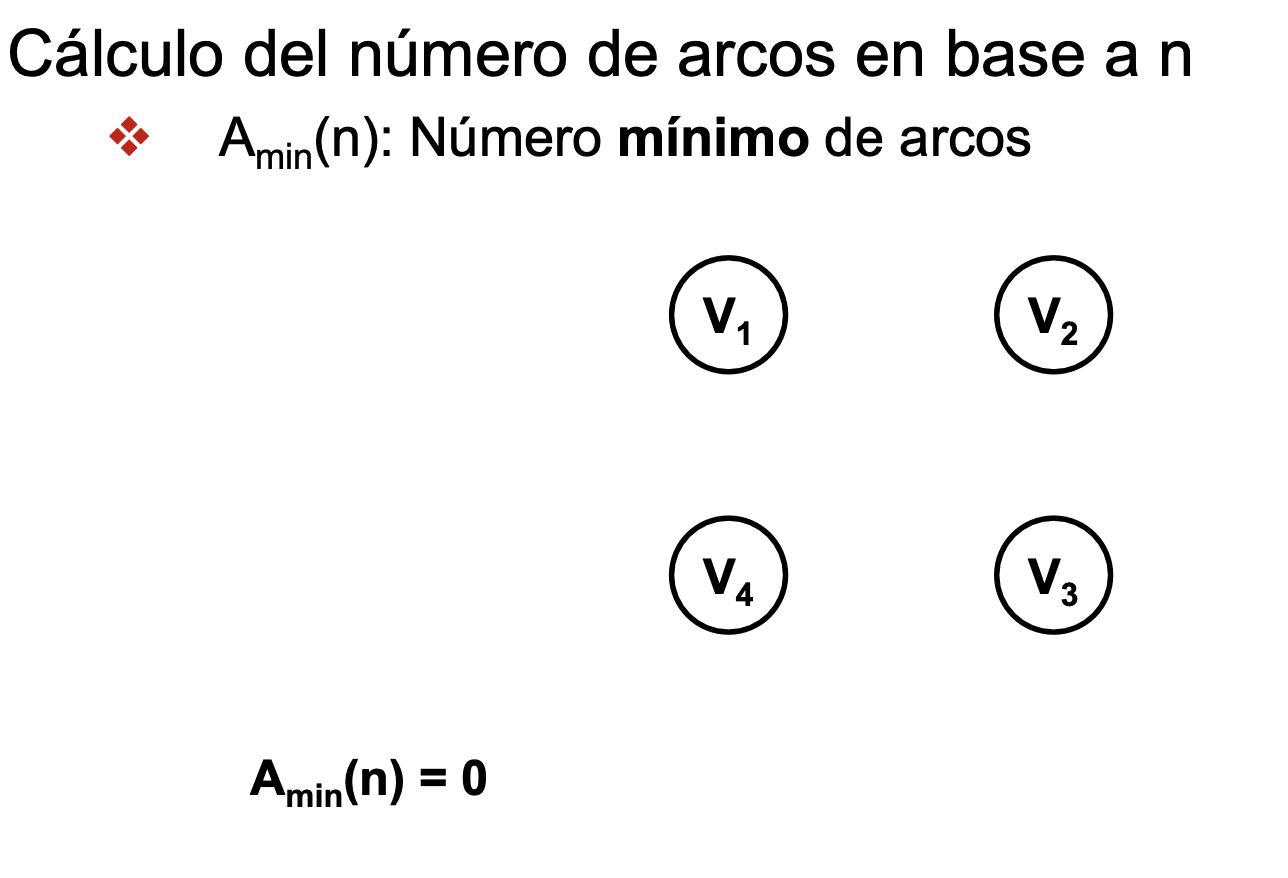
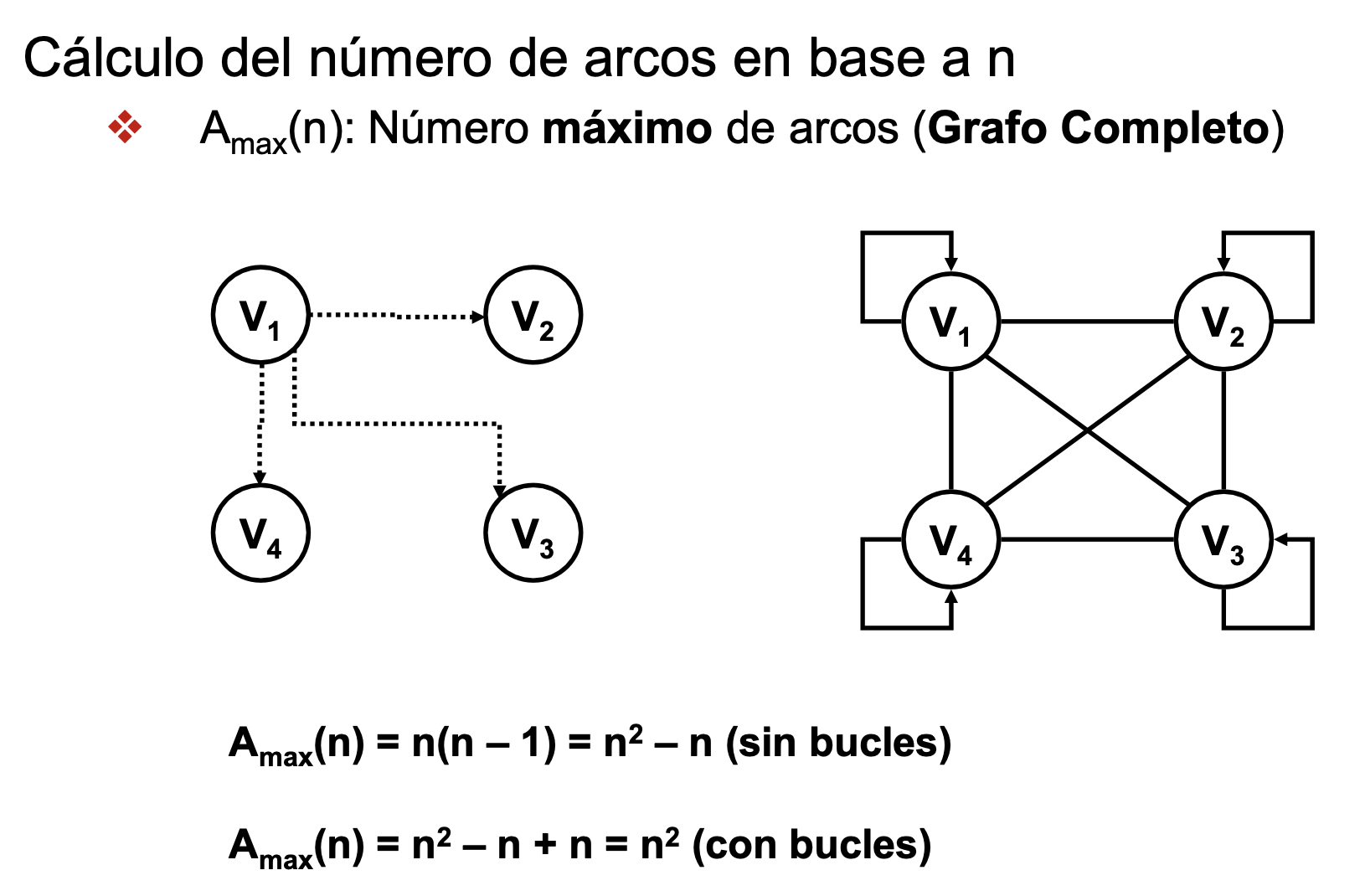
- n = número de nodos de un grafo

- Número mínimo de arcos en un grafo = 0 (todos aislados)
- Número máximo de arcos en un grafo = n^2 (todos conectados con todos (con bucles))
Representación en memoria
Densidad de un grafo

Clase Grafo (Matriz de adyacencias)

- Hay que almacenar los nodos (de cualquier tipo), las aristas y los pesos
| Matrices adyacencias | Listas adyacencias |
|---|---|
- Usan memoria estática 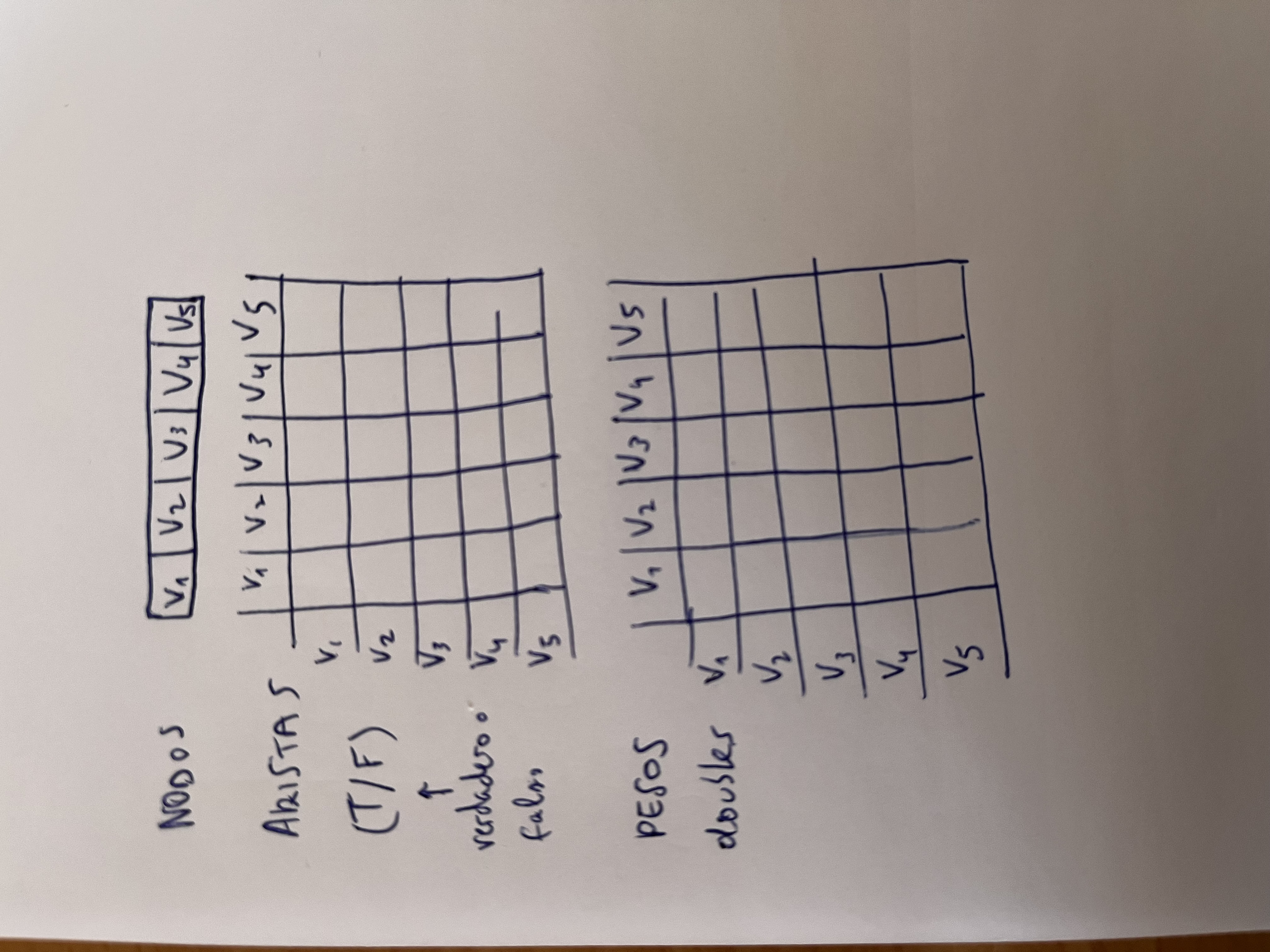 | - Usan memoria dinámica |
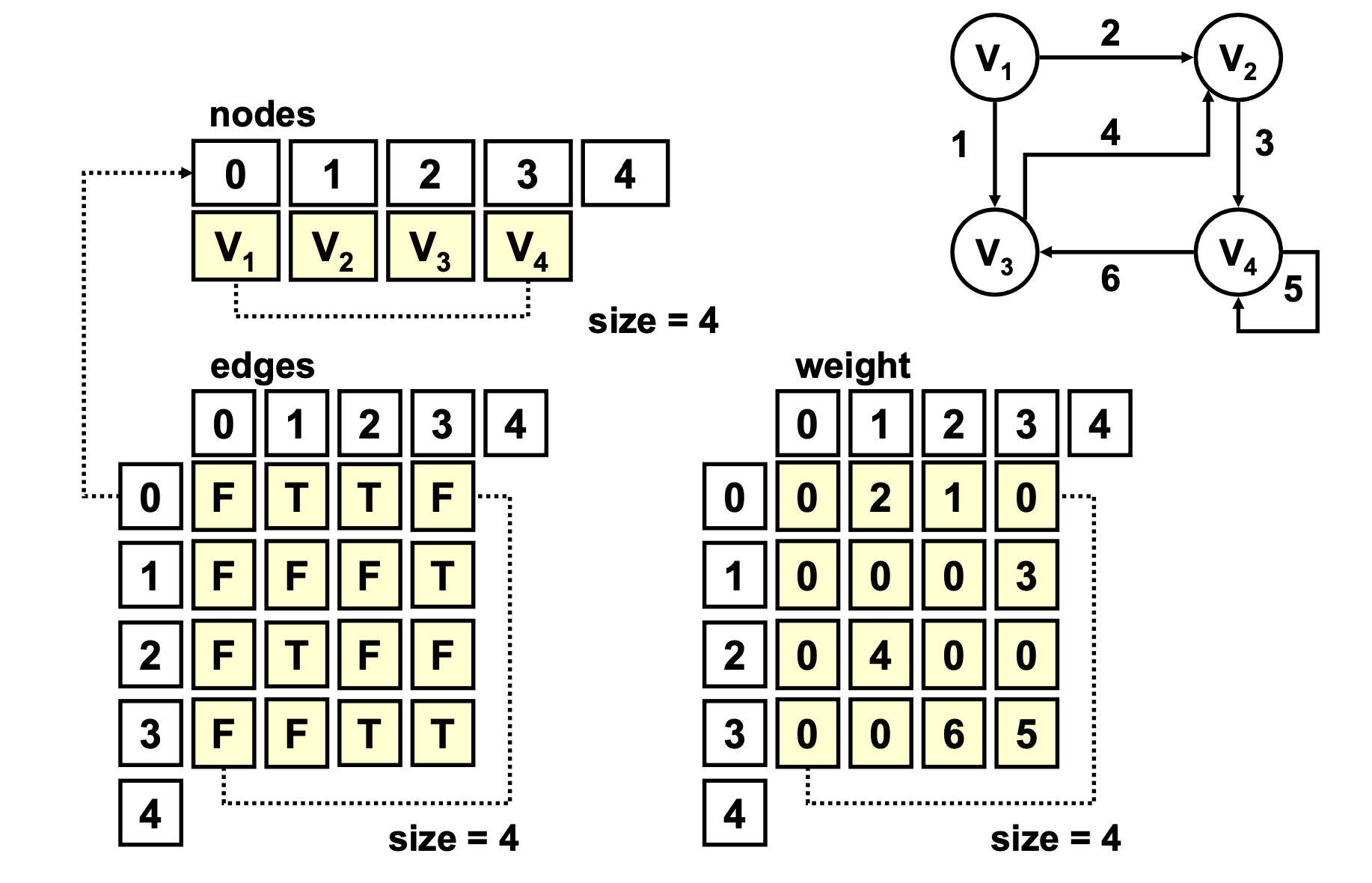
Análisis de eficiencia

Listas de adyacencia

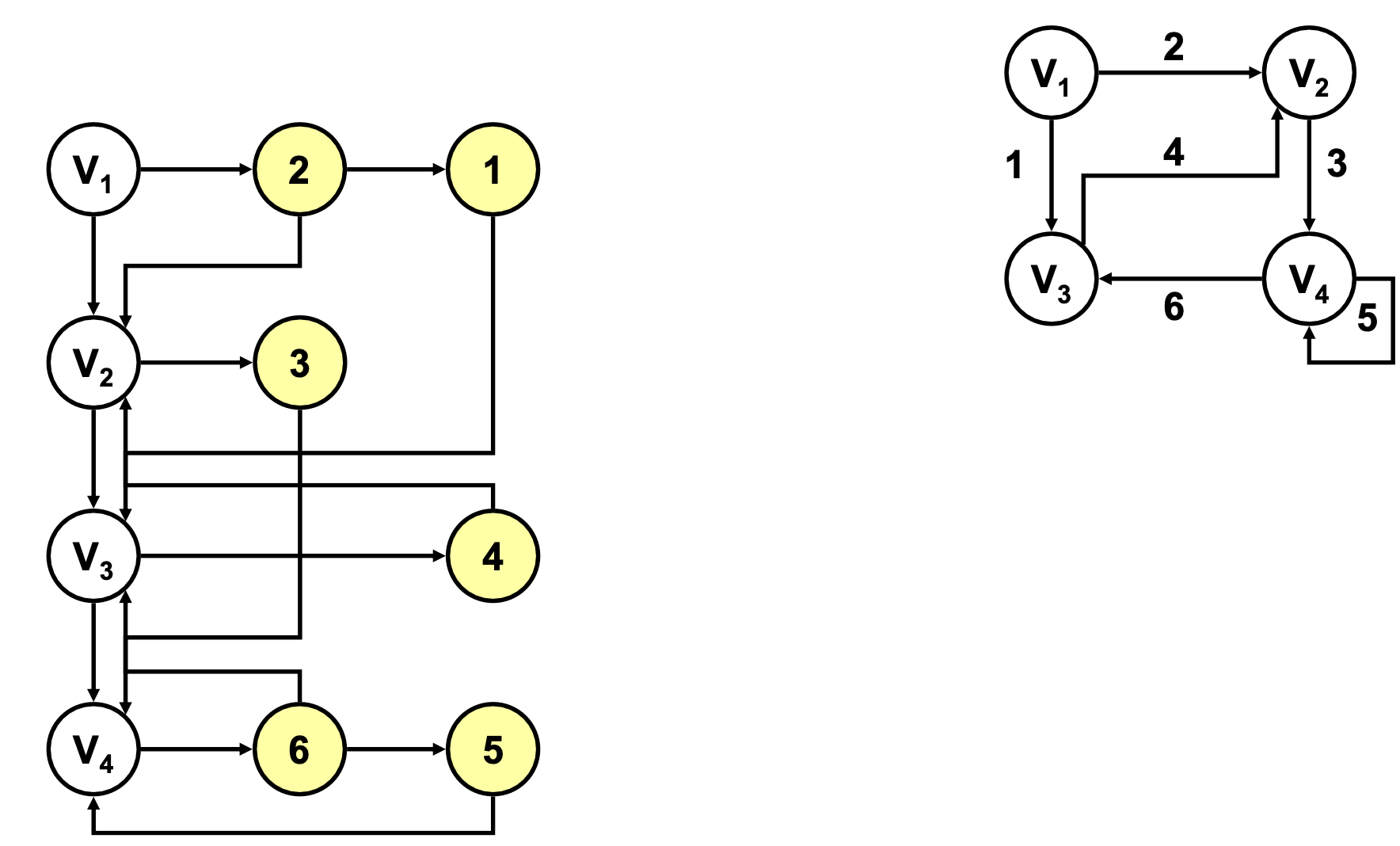
Análisis de Eficiencia

Clase Grafo. Métodos básicos
Matriz de adyacencia
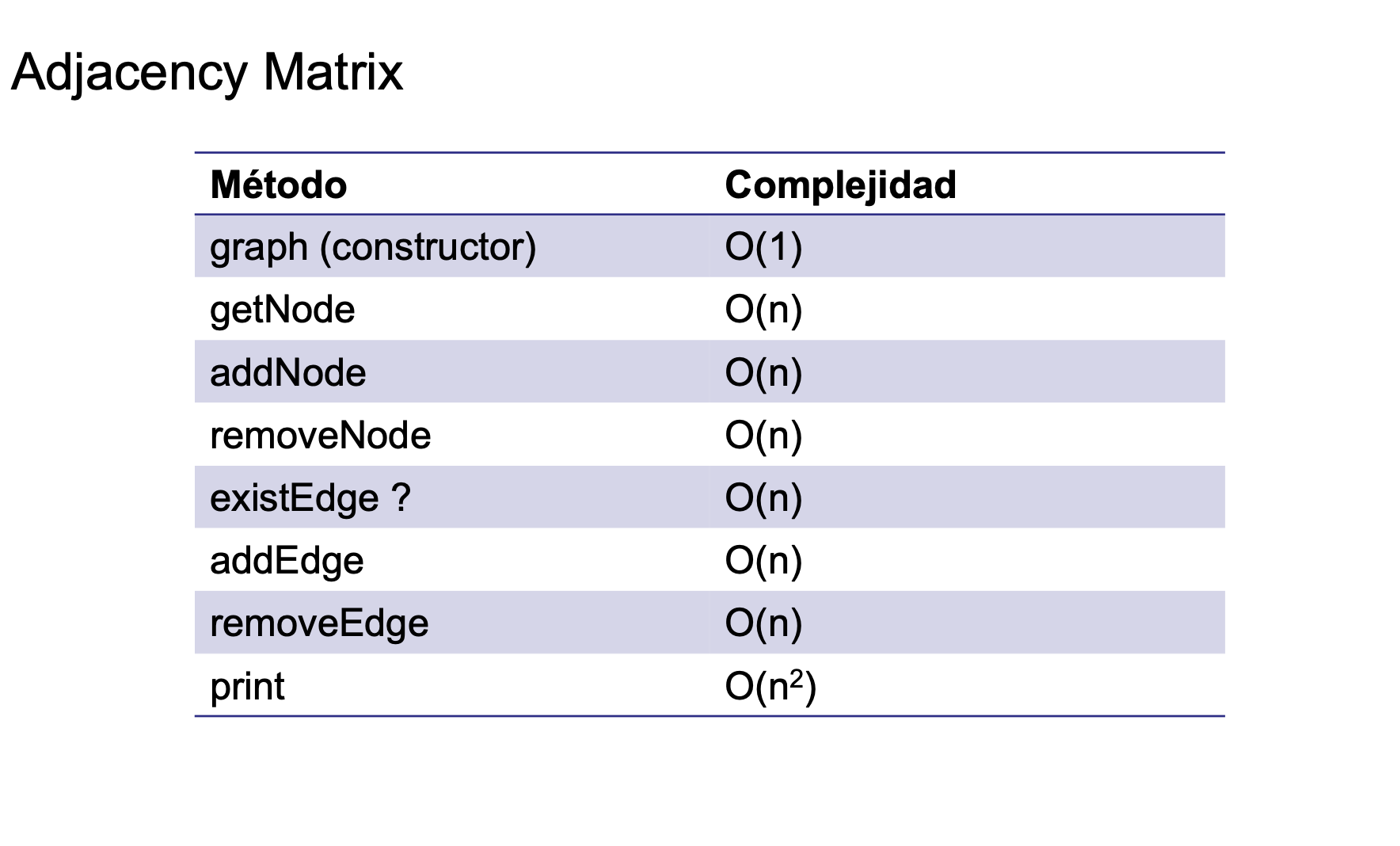
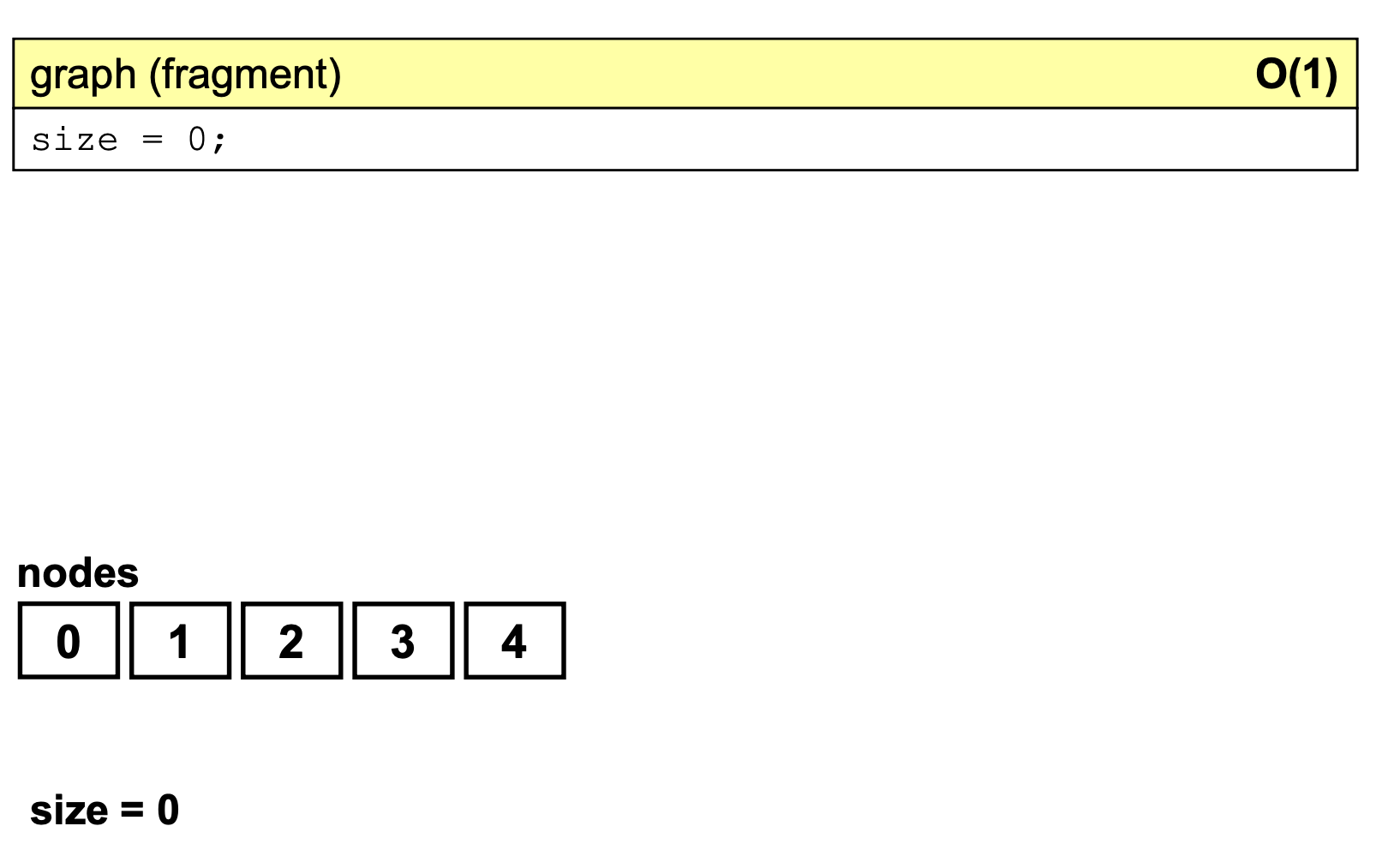
- Complejidad 0(1)
getNode()
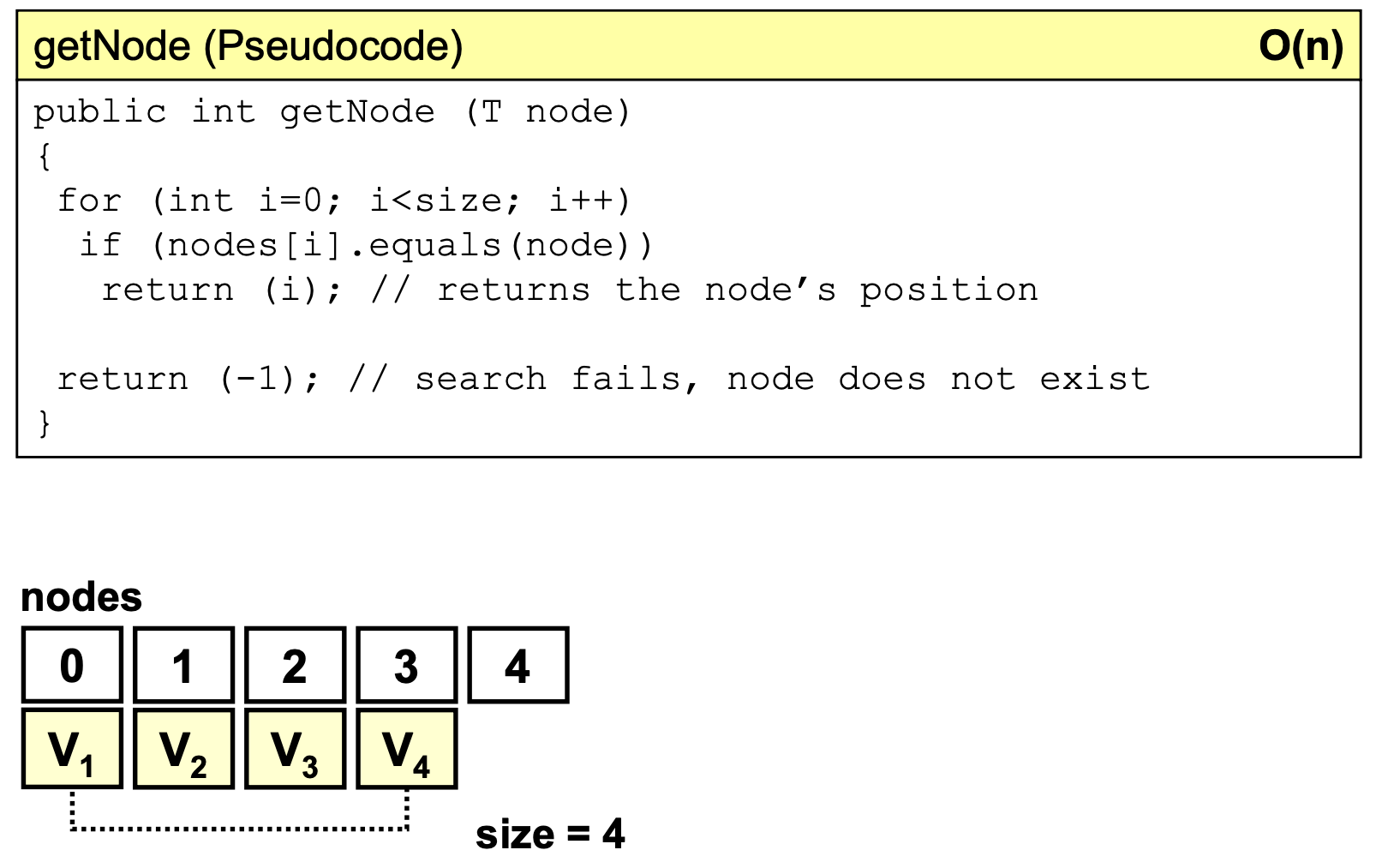
- Complejidad O(n)
public int getNode (T node)
{
for (int i=0; i<size; i++)
if (nodes[i].equals(node))
return (i); // returns the node’s position
return (-1); // search fails, node does not exist
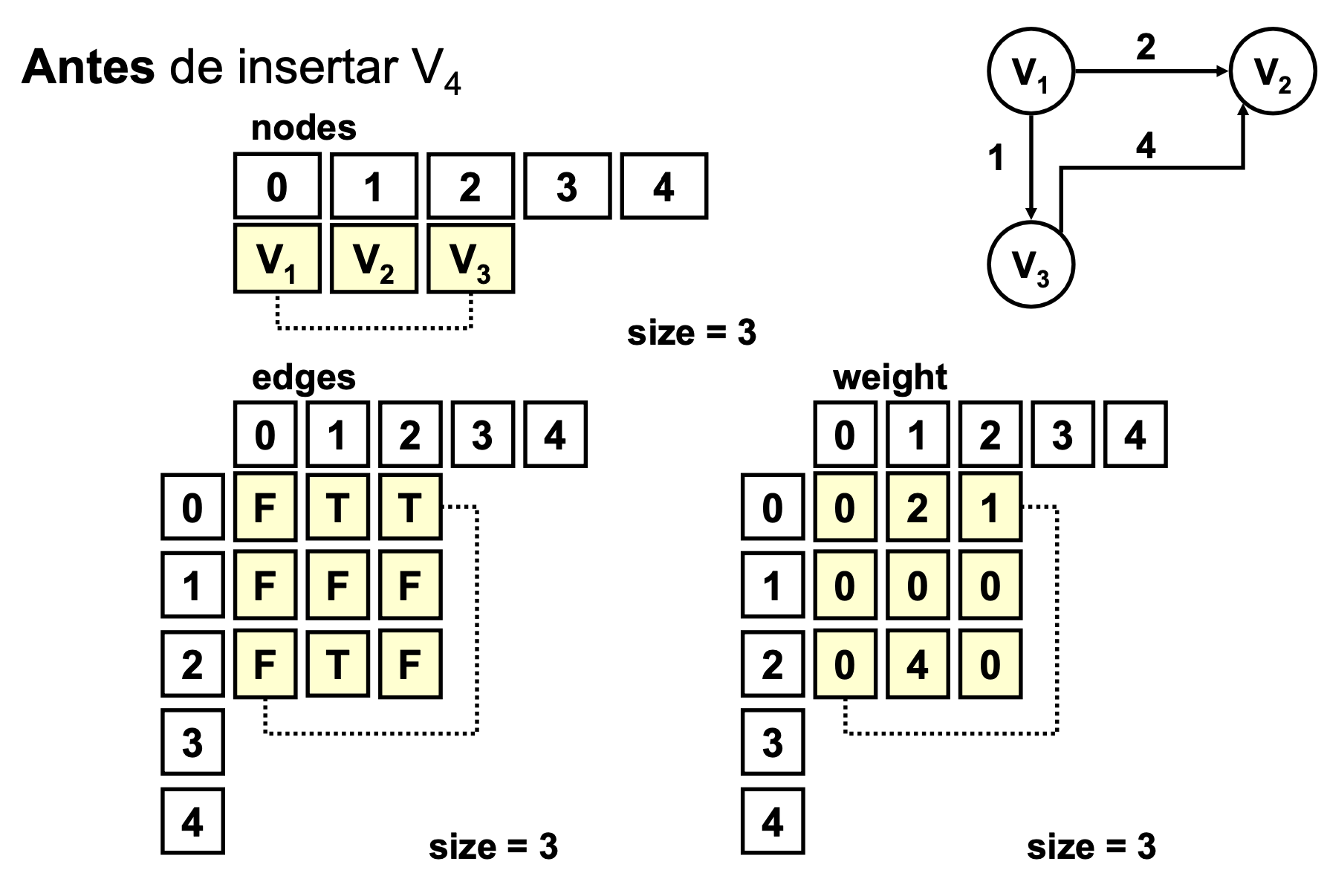
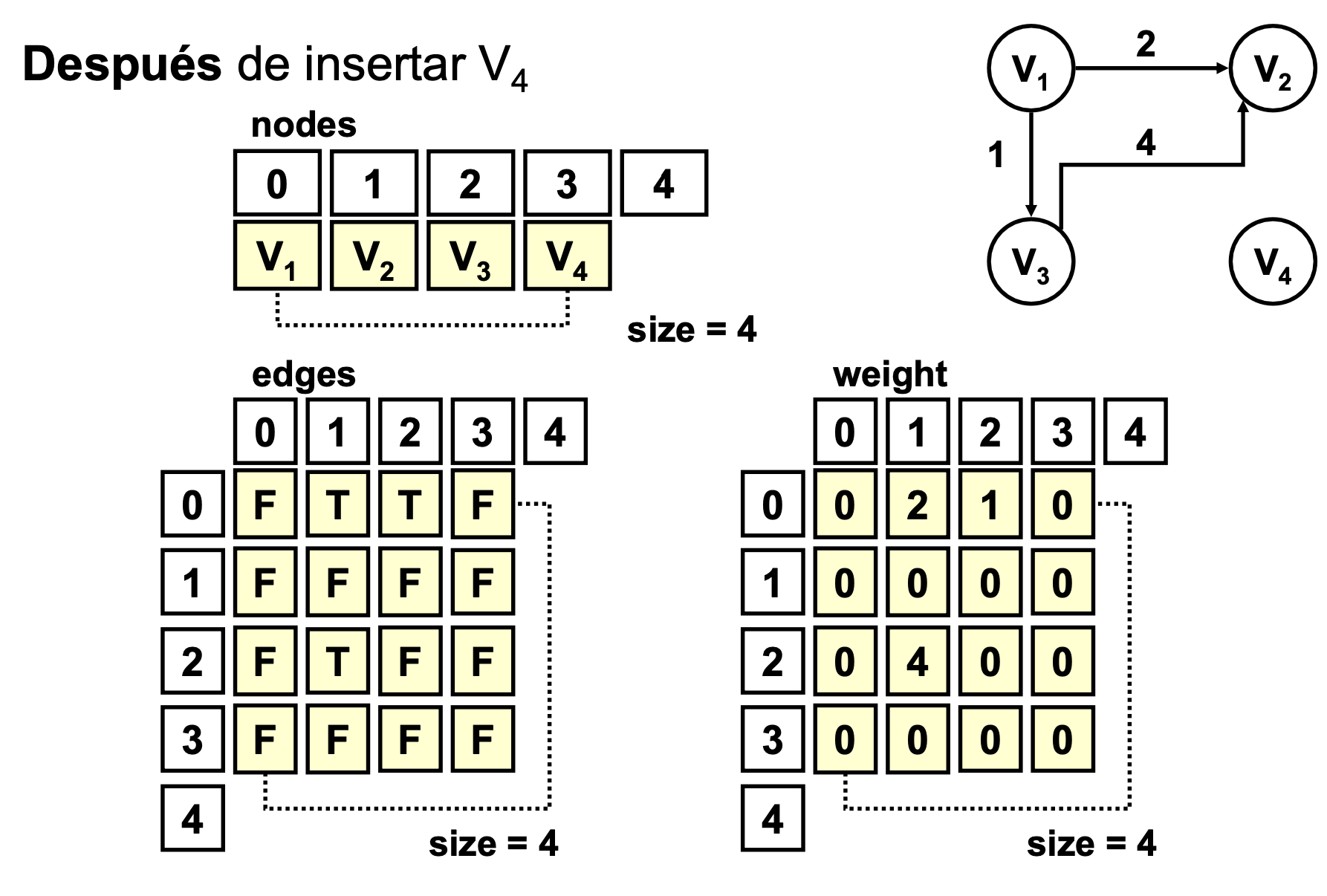
}addNode()

- Complejidad O(n)
public void addNode (T node)
{
// precondition: node does not exits and there is
// available space for the node.
if (getNode(node)== -1 && size<nodes.length)
{
nodes[size] = node;
//inserts void edges
for (int i=0; i<=size; i++)
{
edges[size][i]=false;
edges[i][size]=false;
weight[size][i]=0;
weight[i][size]=0;
}
++size;
}
}
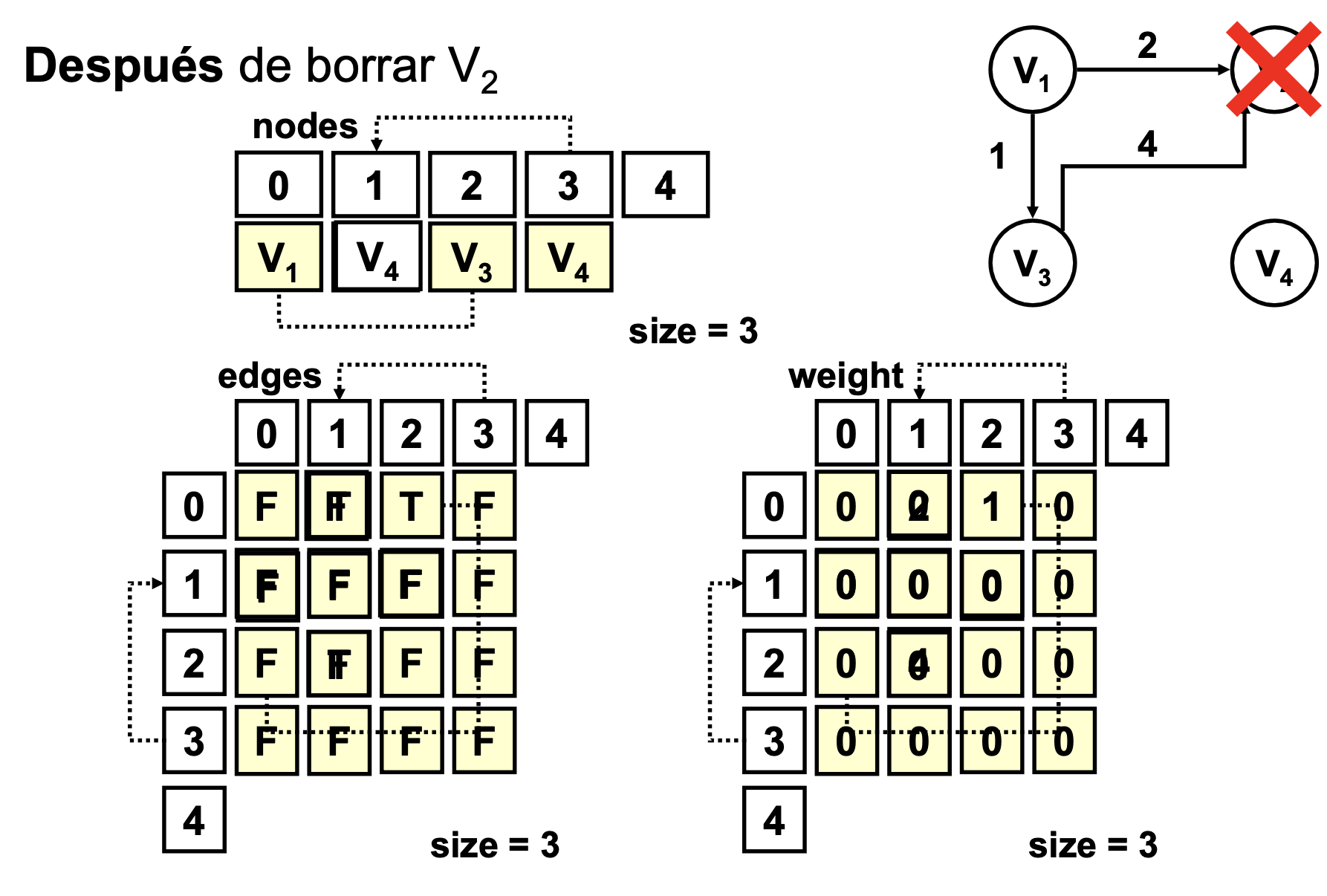
removeNode()

- Complejidad O(n)
public void removeNode (T node){
int i = getNode(node);
if (i>=0) {
--size;
if (i != size+1) { // it is not the last node
nodes[i] = nodes[size]; //replaces by the last node
//replace elements in the vectors edges and weights
for (int j=0; j<=size; j++) {
edges[j][i]=edges[j][size];
edges[i][j]=edges[size][j];
weight[i][j]=weight[size][j];
weight[j][i]=weight[j][size];
}
// loop (diagonal)
edges[i][i] = edges[size][size];
weight[i][i] = weight[size][size];
}
}existsEdge()

- Complejidad O(n)
public boolean existsEdge (T origin, T destination)
{
int i=getNode(origin);
int j=getNode(destination);
// precondition: both nodes must exist. // if don’t... should we throw an exception?
if (i>=0 && j>=0)
return(edges[i][j]);
else
return (false);
}addEdge()

- Complejidad O(n)
public void addEdge (T origin, T destination, double
edgeWeight)
{
// precondition: the edge must not already exist.
if (!existEdge(origin, destination))
{
int i=getNode(origin);
int j=getNode(destination);
edges[i][j]=true;
weight[i][j]=edgeWeight;
}
else
; // what about throwing an exception here?
}removeEdge()

- Complejidad O(n)
public void removeEdge (T origin, T destination){
// precondition: the edge must exist.
if (existsEdge(origin, destination)) {
int i=getNode(origin);
int j=getNode(destination);
edges[i][j]=false;
weight[i][j]=0.0;
}
else
; // what about throwing an exception?
}print()

- Complejidad O(n^2)
public void print(){
for (int k=0; k<size; k++)
nodes[k].print();
for (int i=0; i<size; i++) {
for (int j=0; j<size; j++) {
System.out.print(edges[i][j] + “(“);
System.out.print(weight[i][j] + “) “);
}
System.out.println();
}Más conceptos básicos
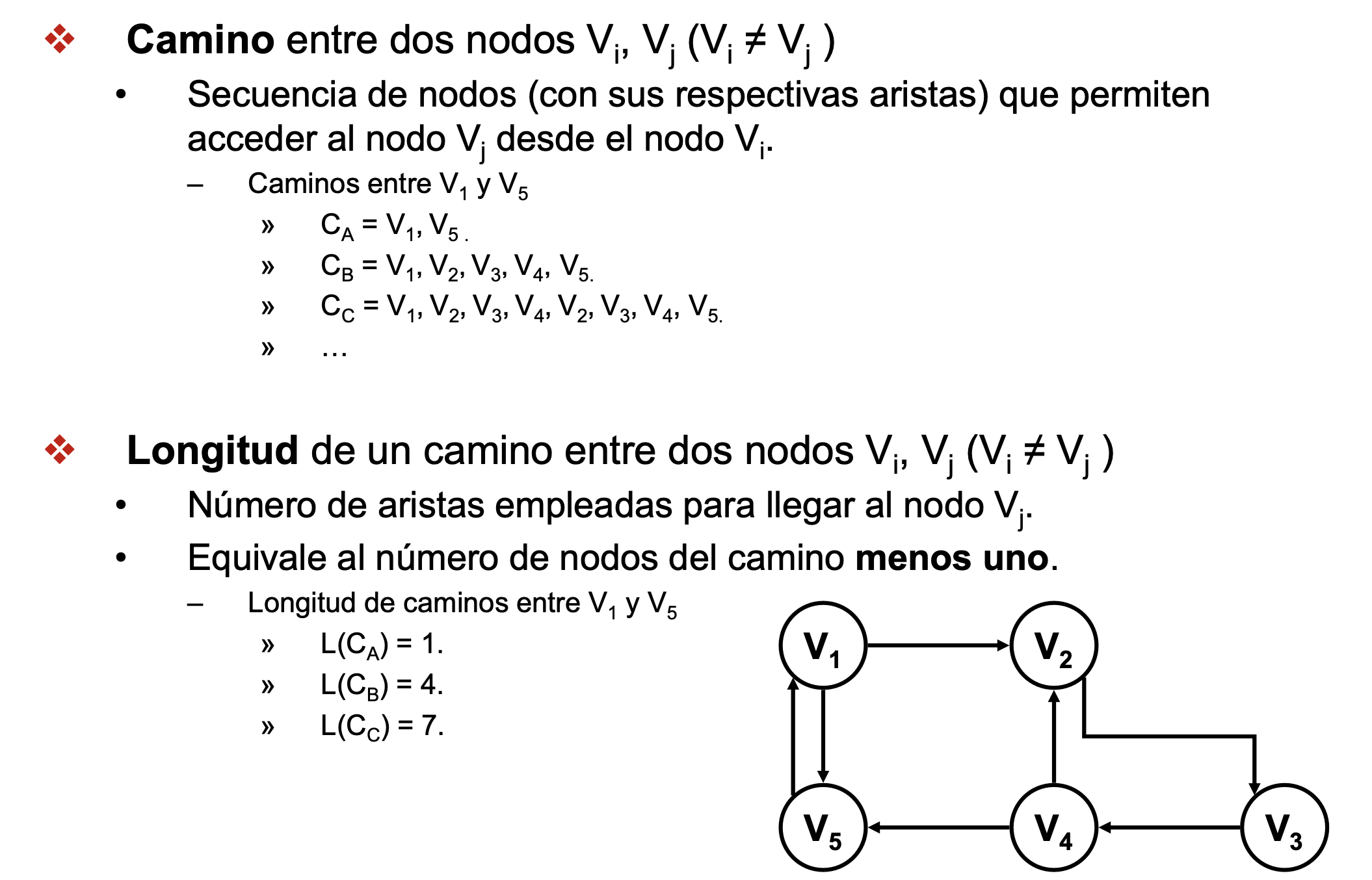
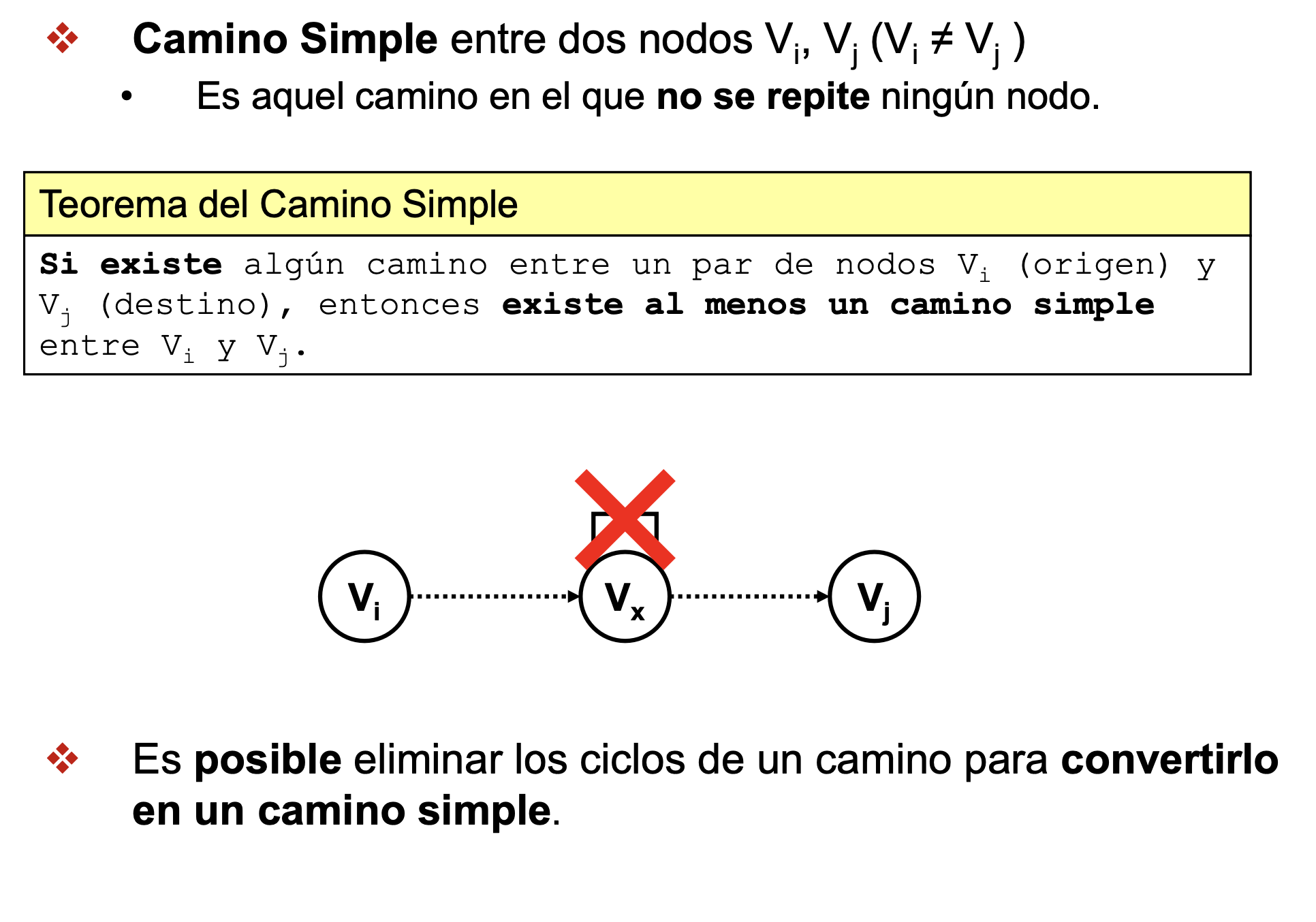
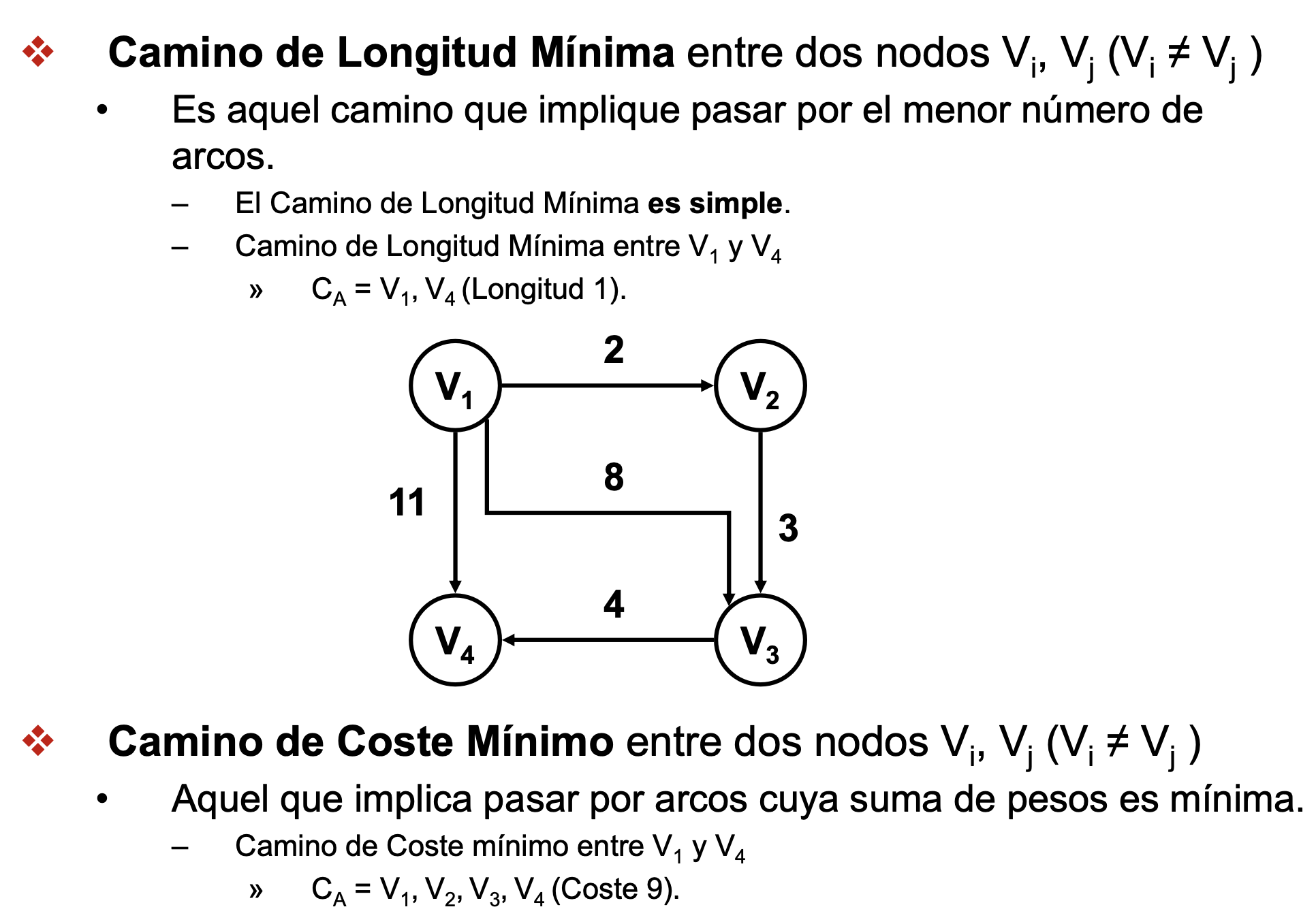
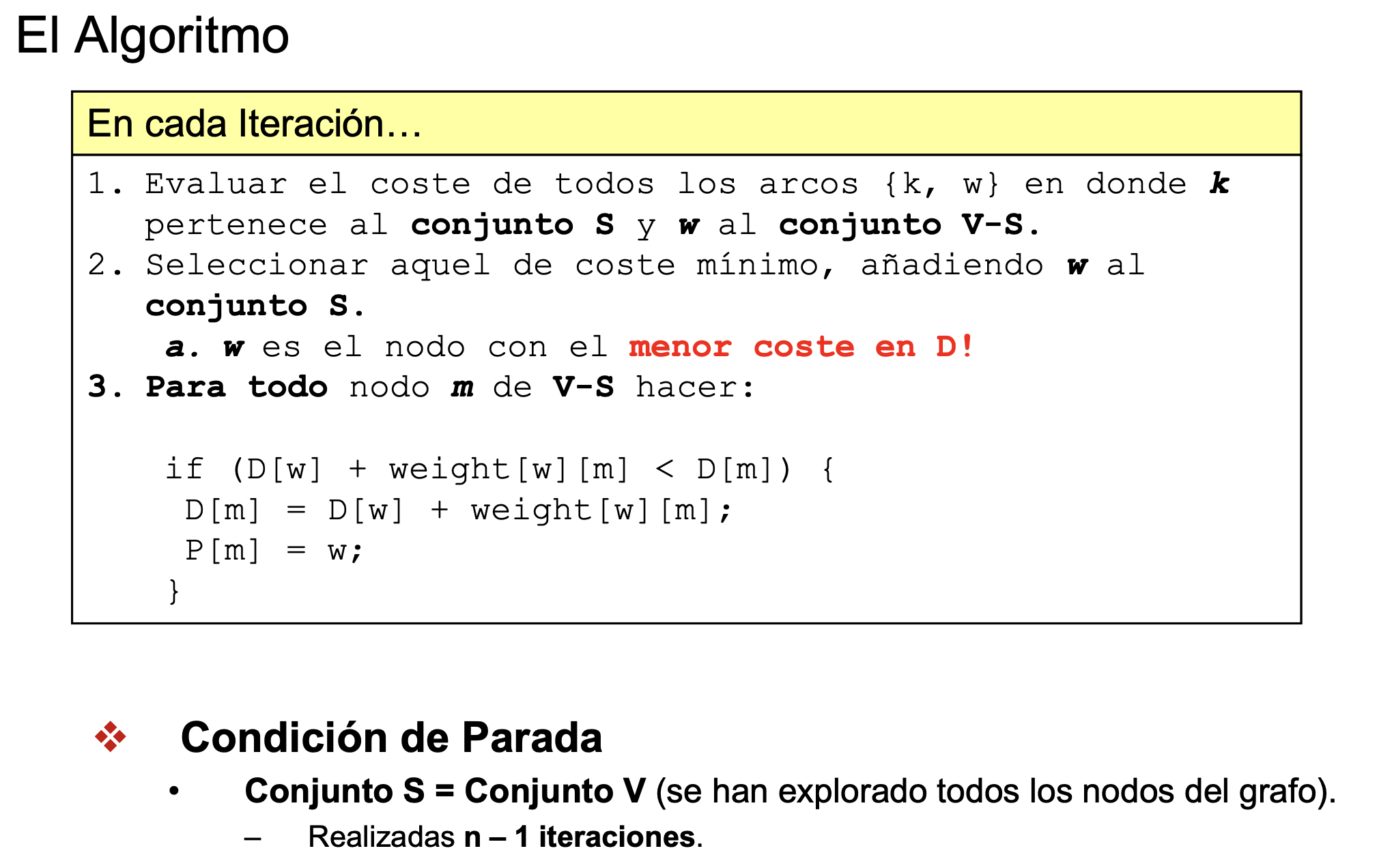
Algoritmo de Dijkstra

- Va de un nodo origen al resto
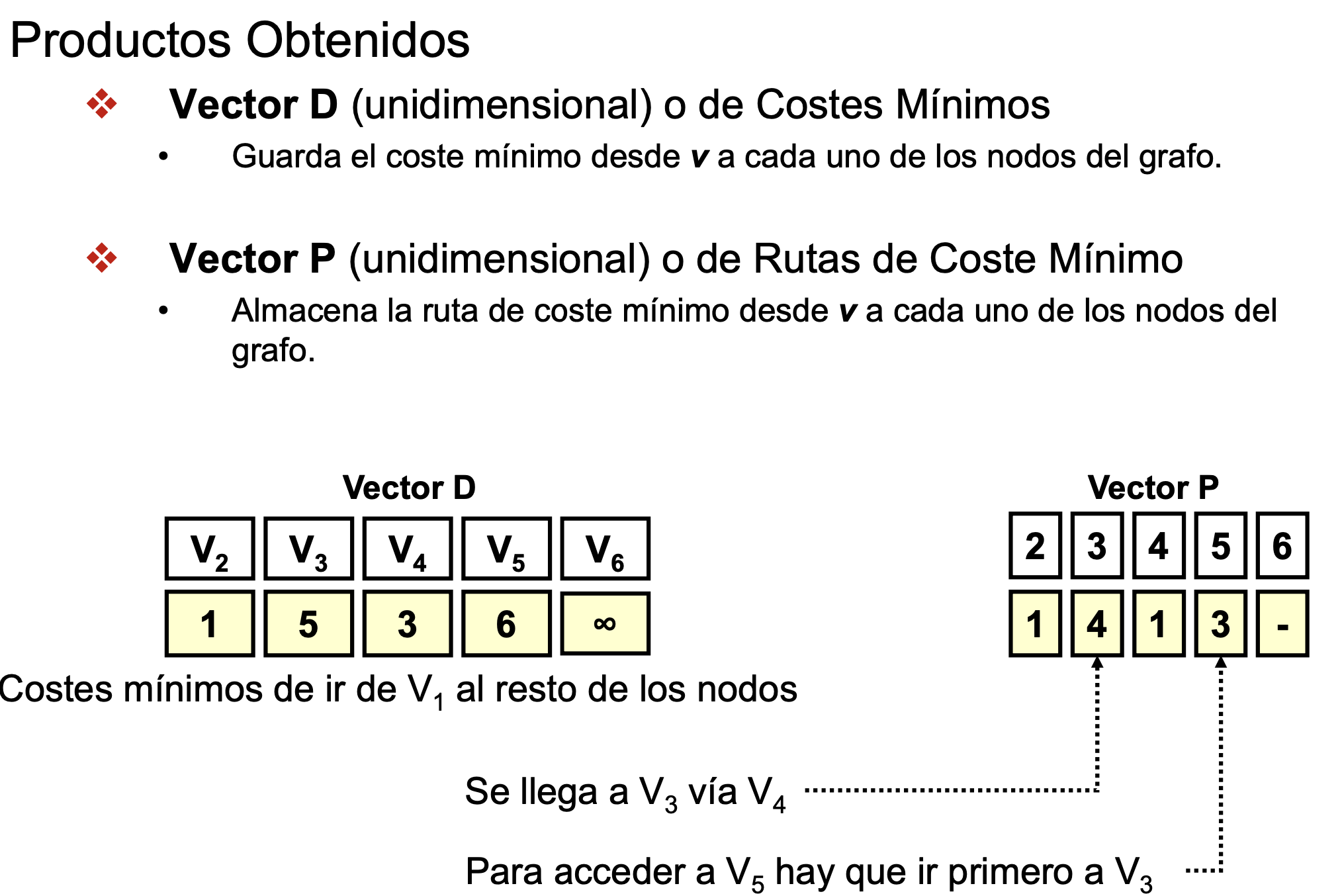
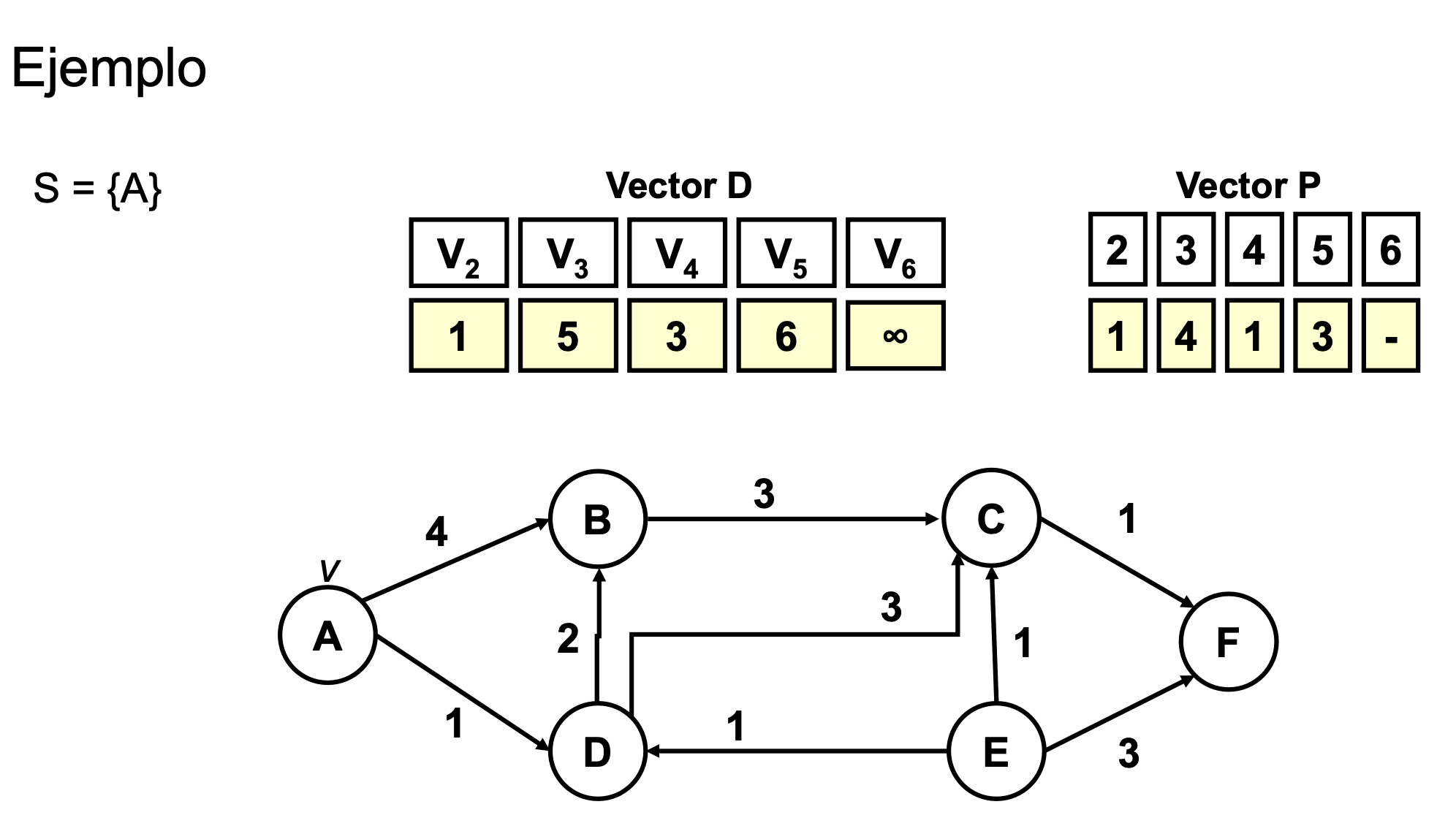
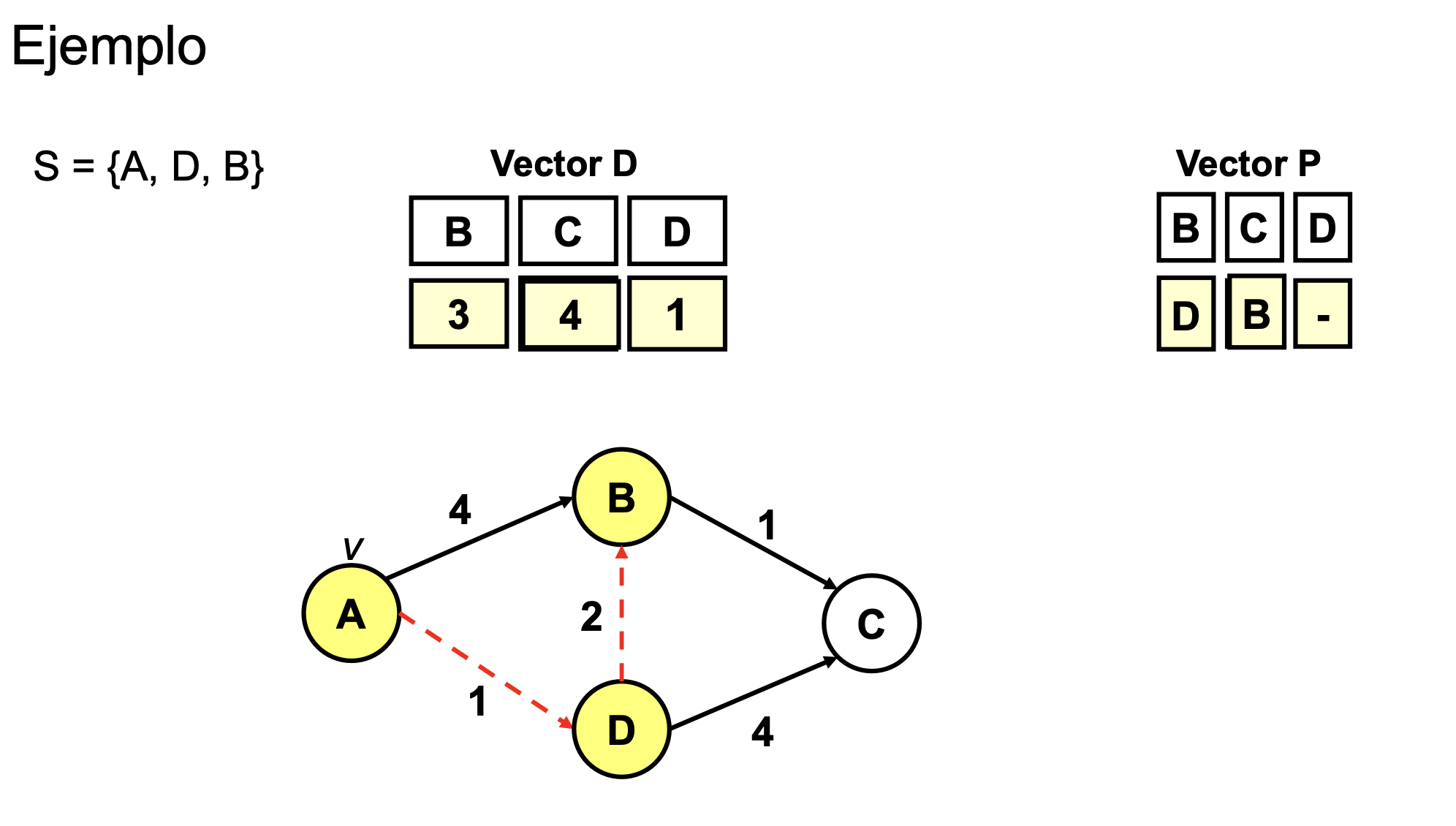
Ejemplo
Inicialización

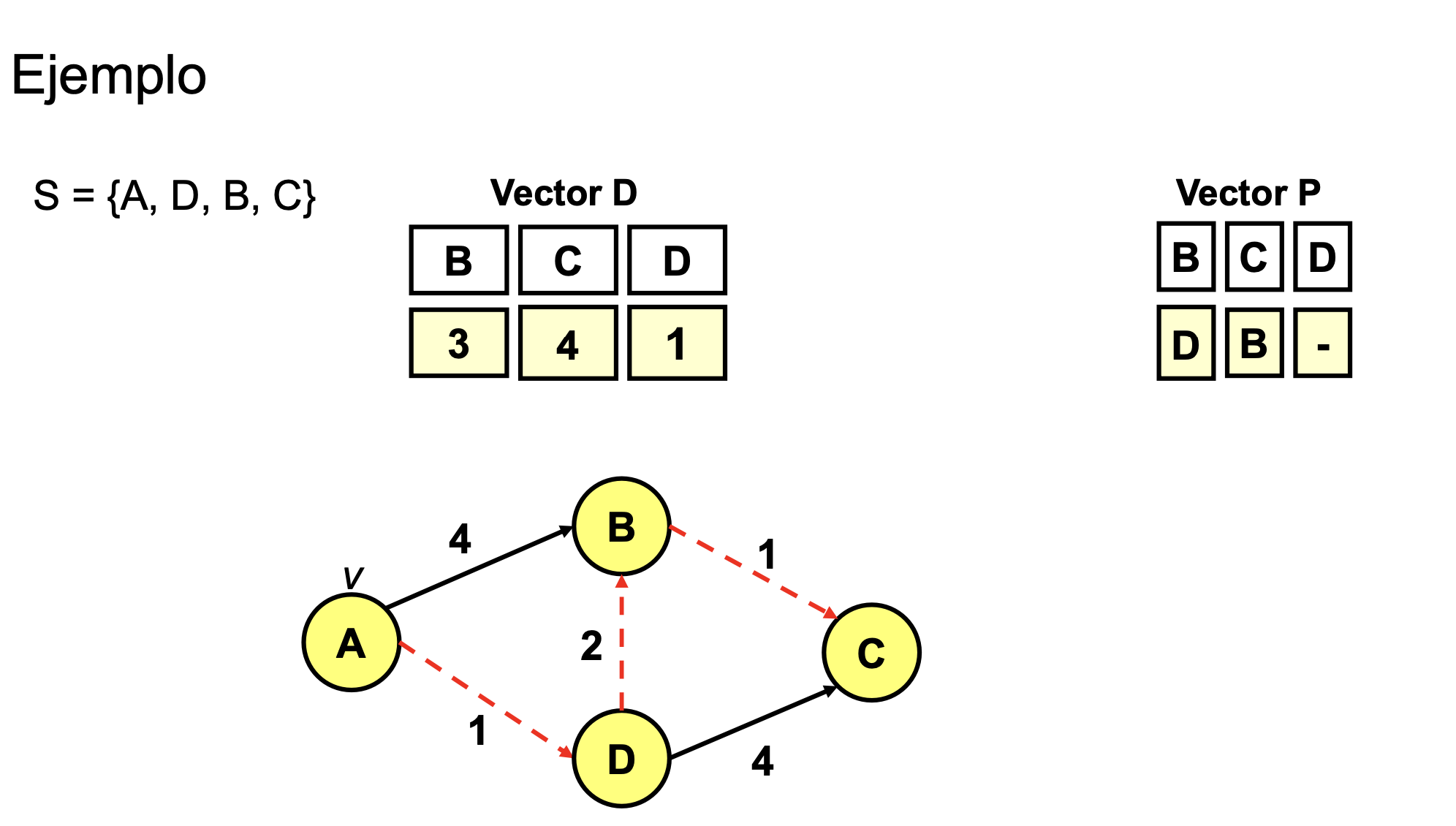
- Dijkstra es un algoritmo devorador (una vez que ha elegido a un nodo, no lo vuelve a usar)
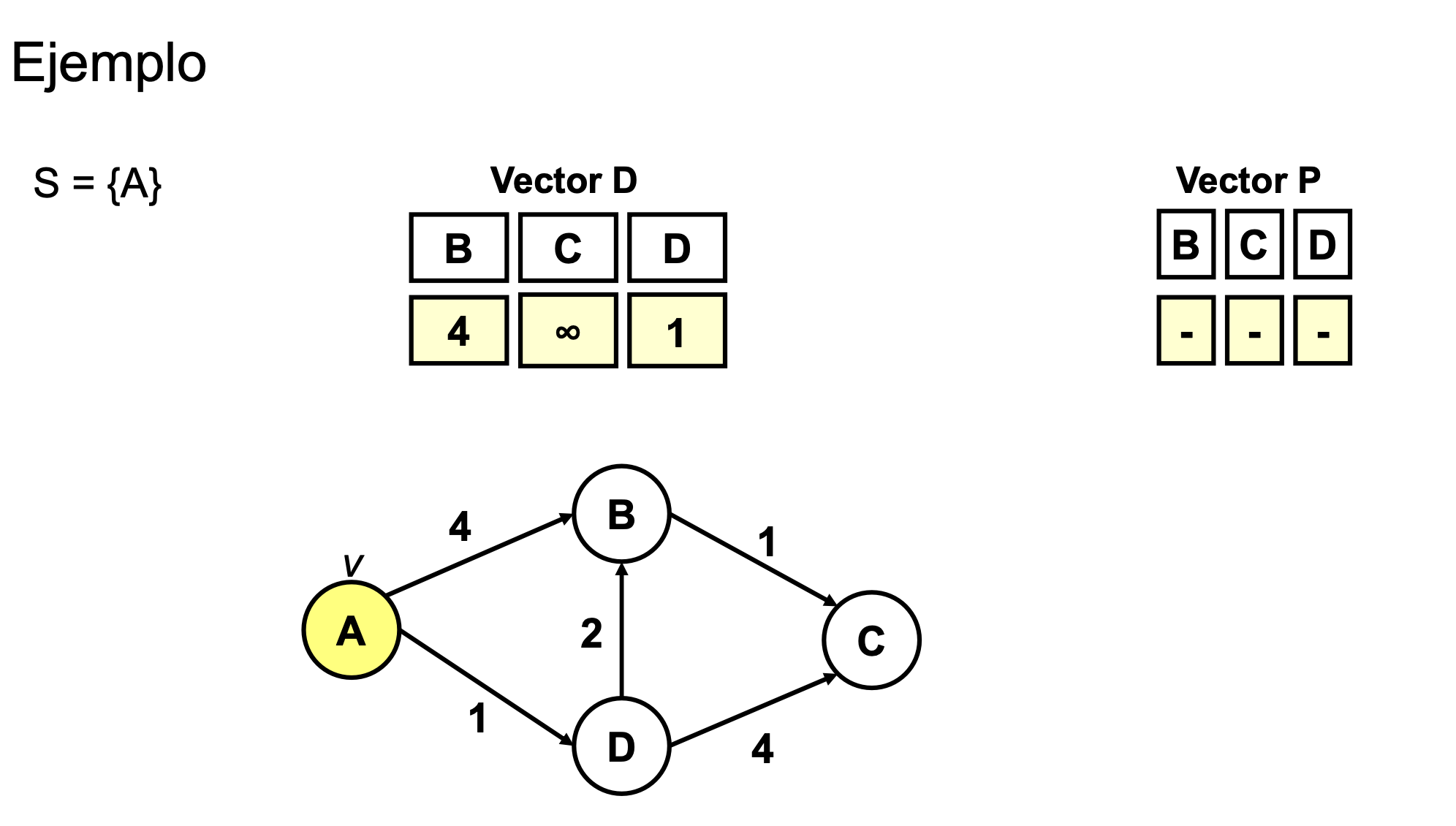
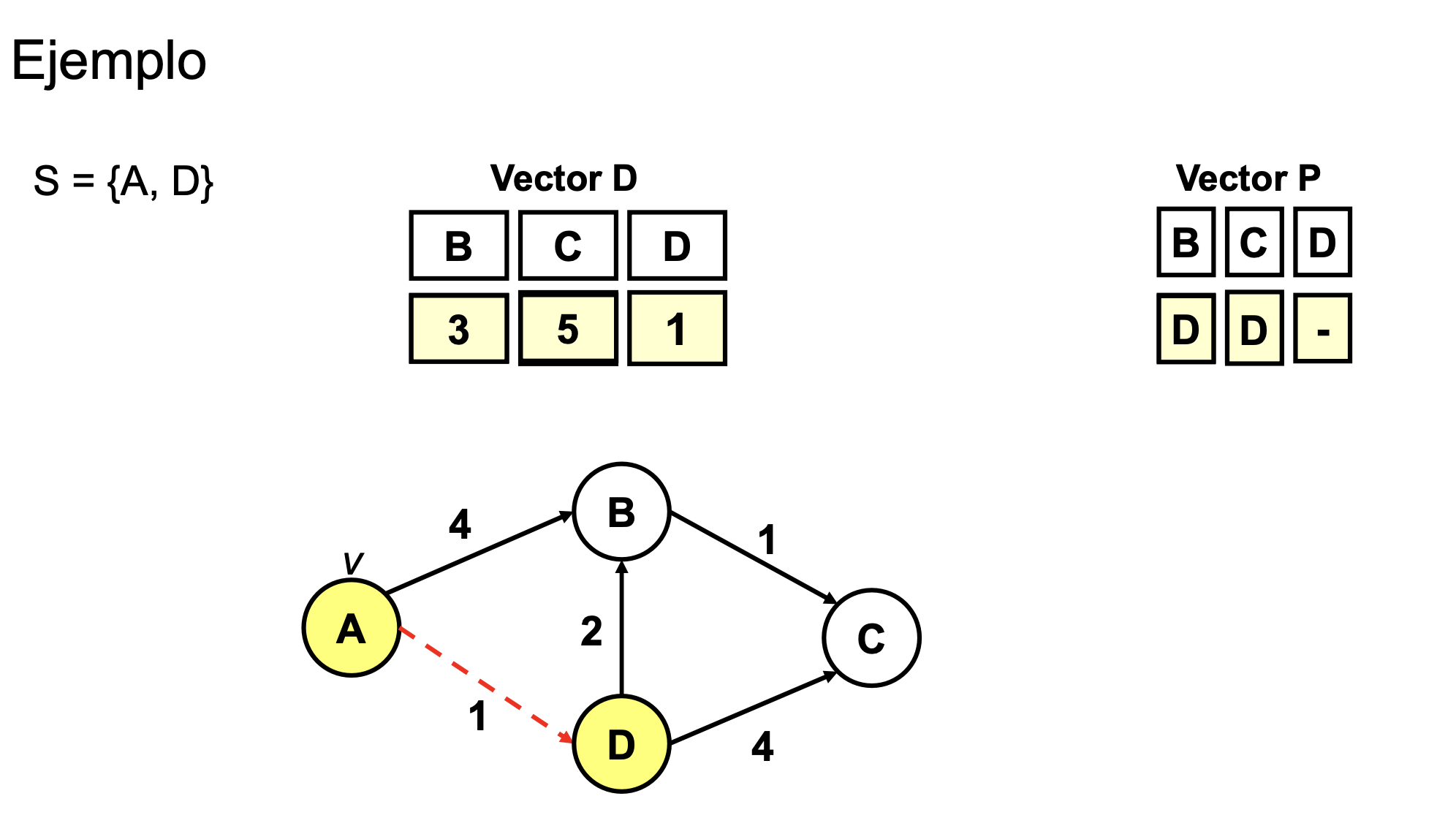
Ejemplo
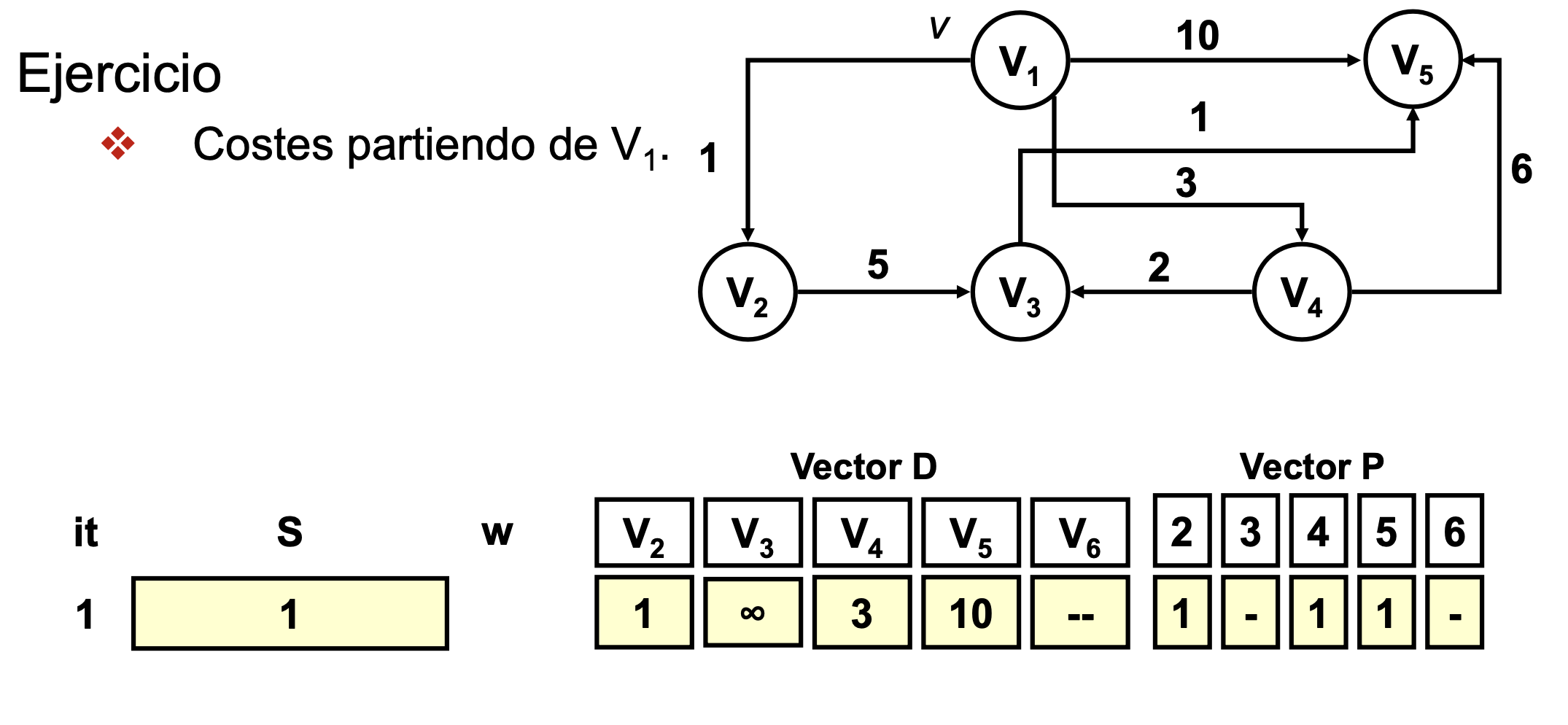
Ejercicio Dijkstra
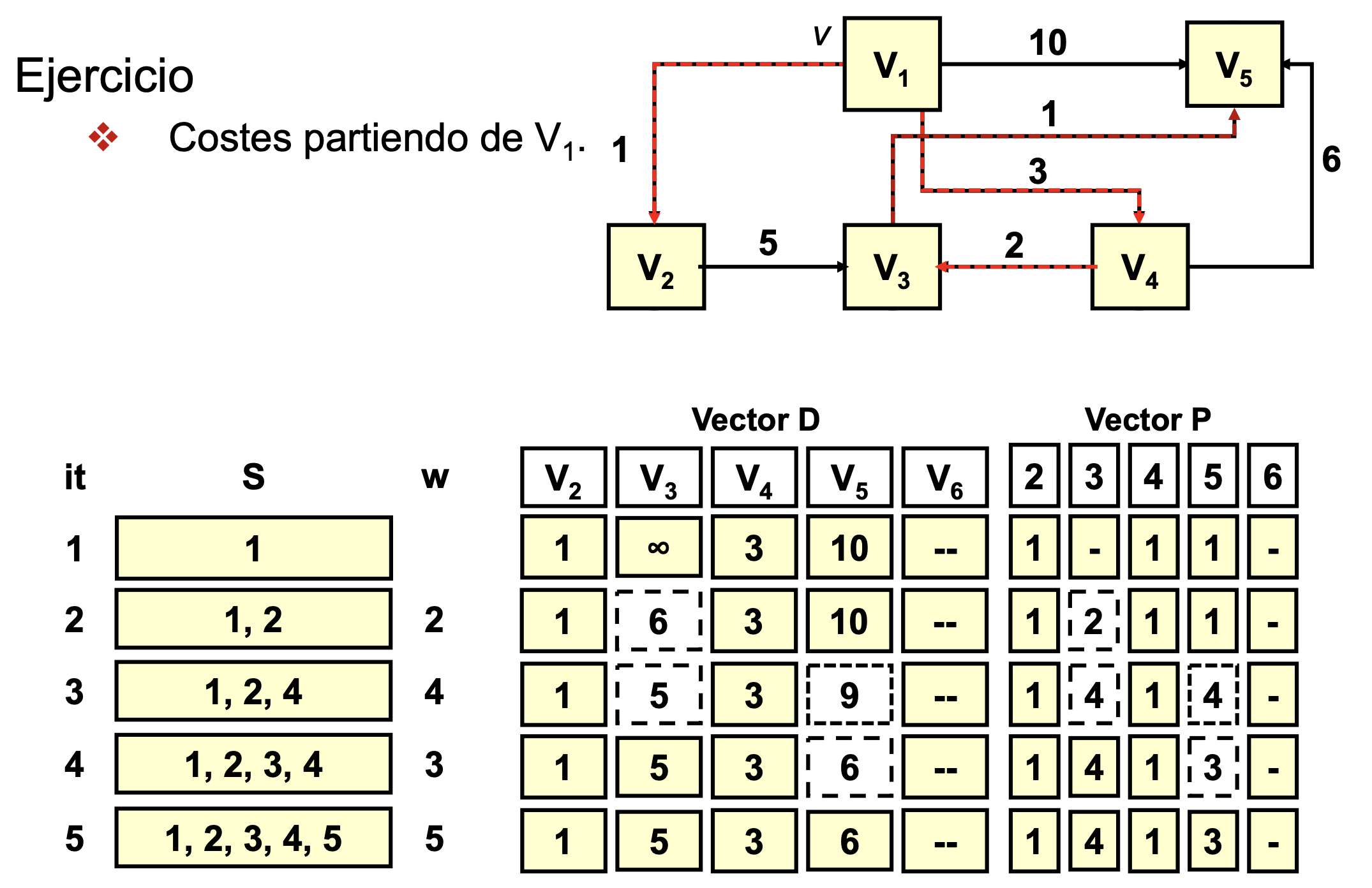
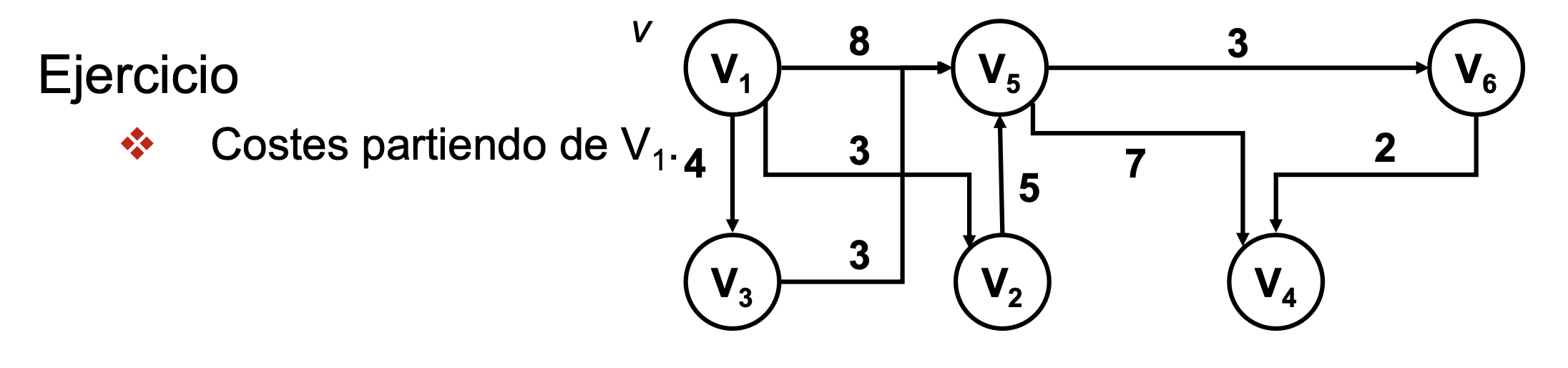
Ejercicio

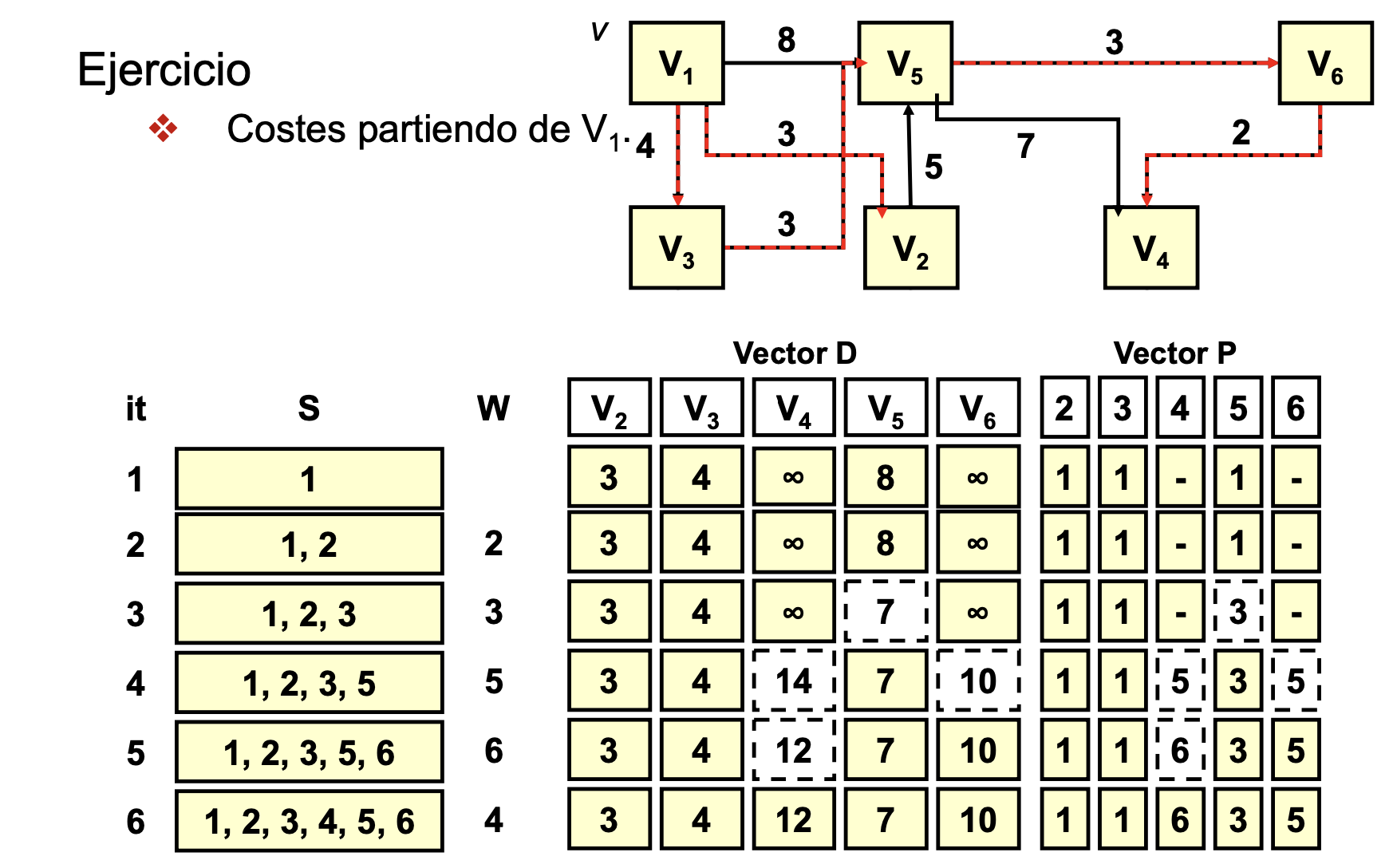
Conclusiones
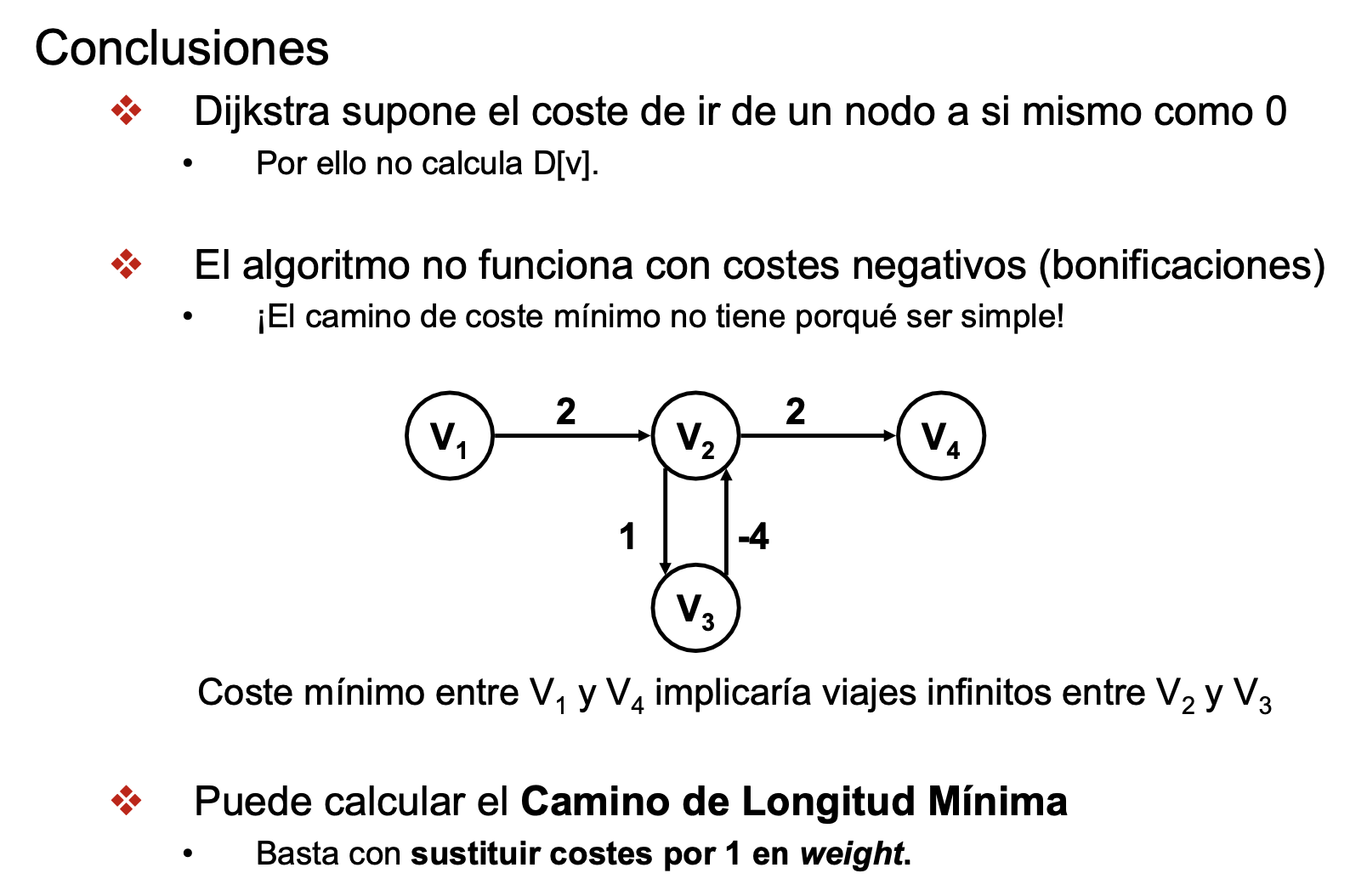
- Dijkstra tiene una complejidad cuadrática O(n^2)
Algoritmo de Floyd-Warshall

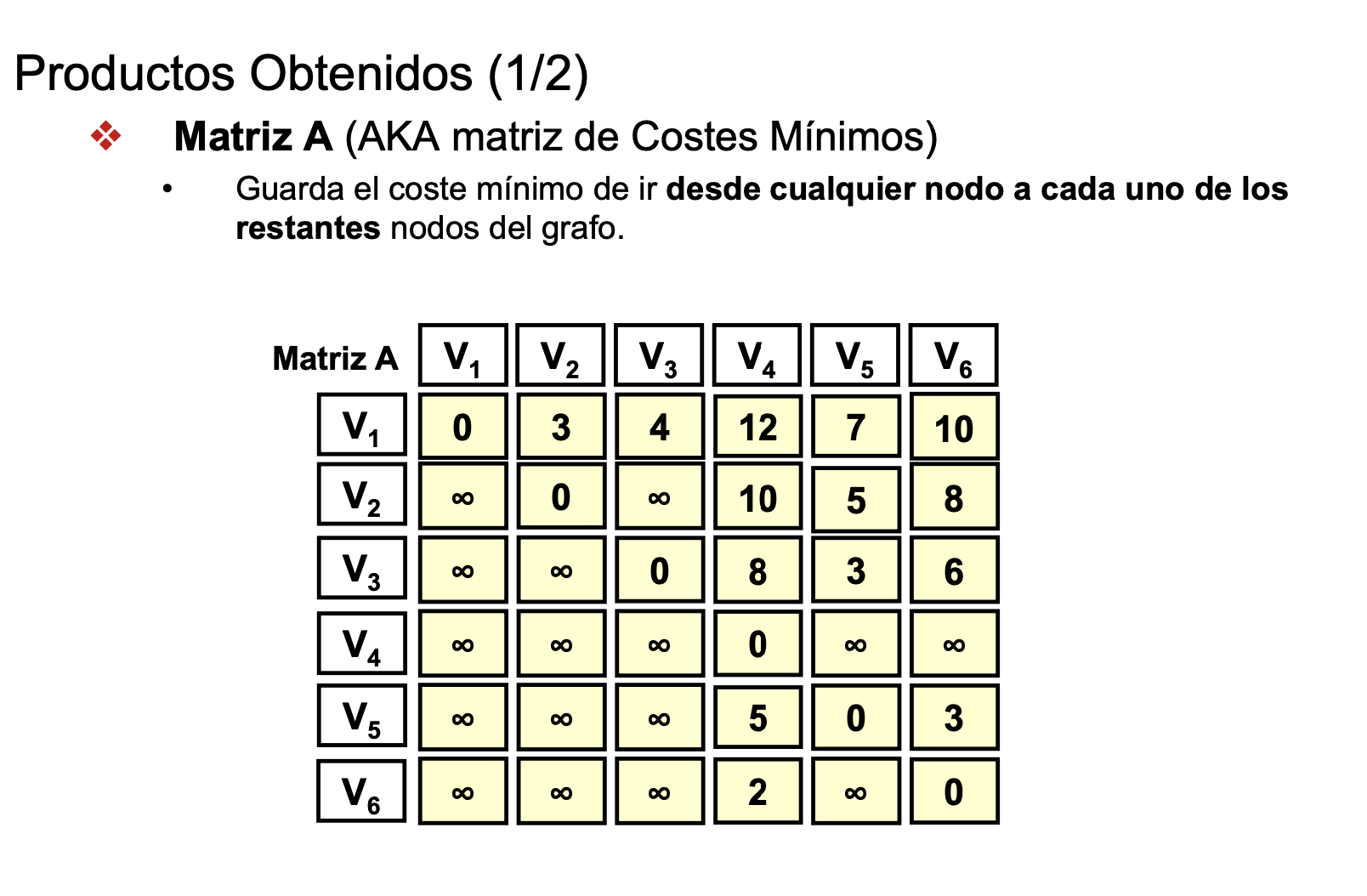

Inicialización de la Matriz A

El algoritmo

- k es el pivote
- i es el origen
- j es el destino
Ejemplo 1 de Floyd-Warshall
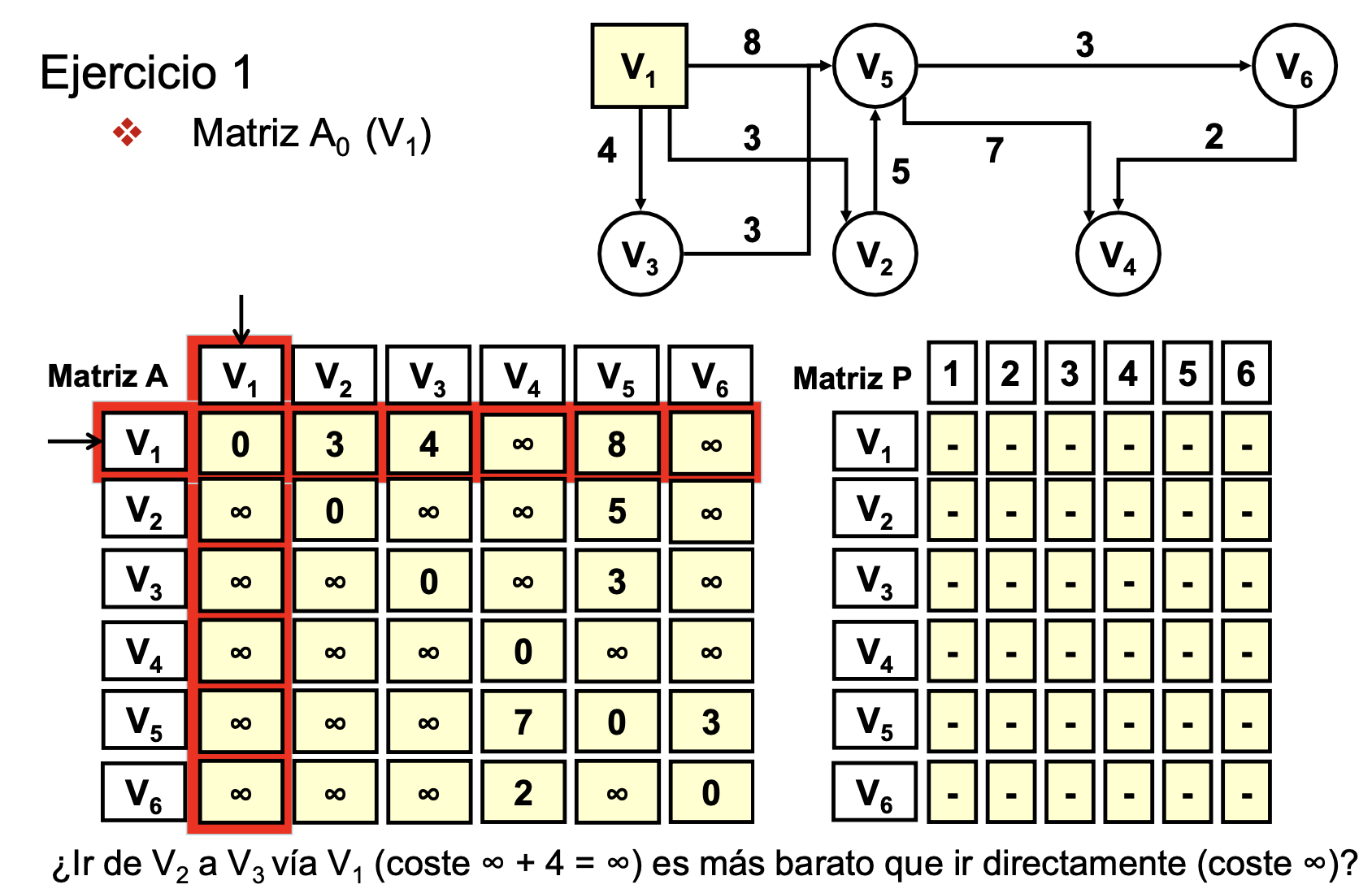
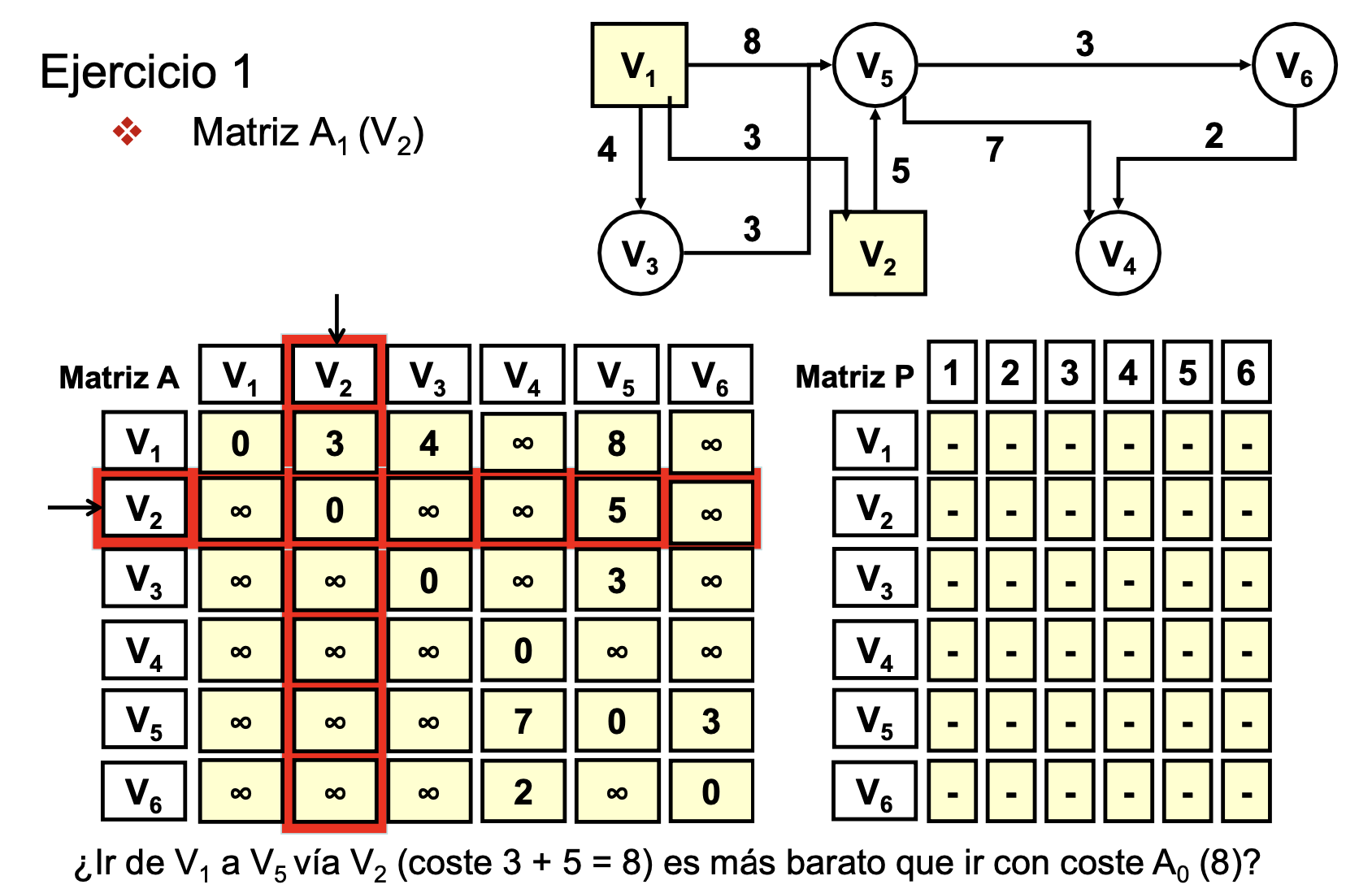
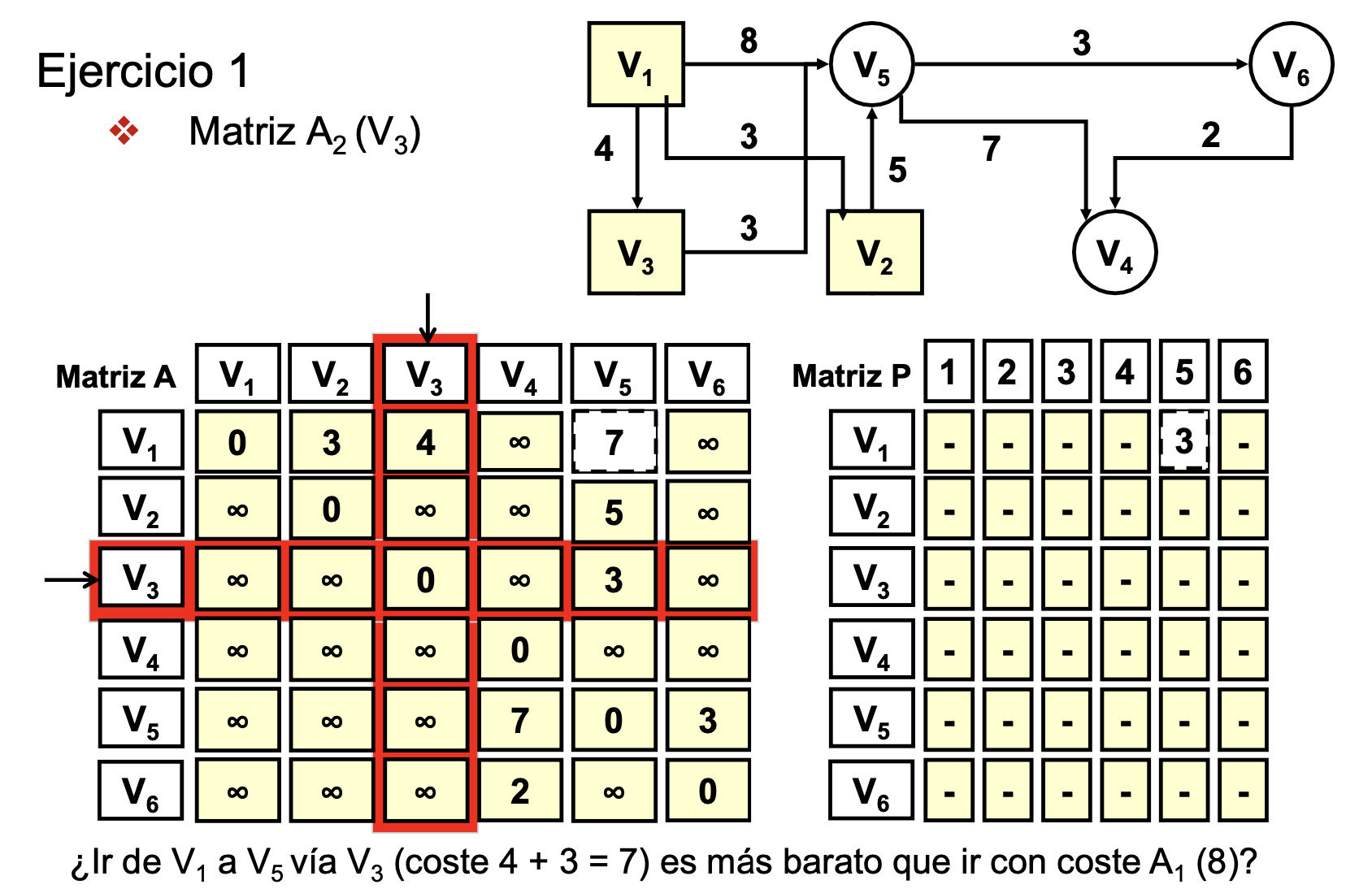
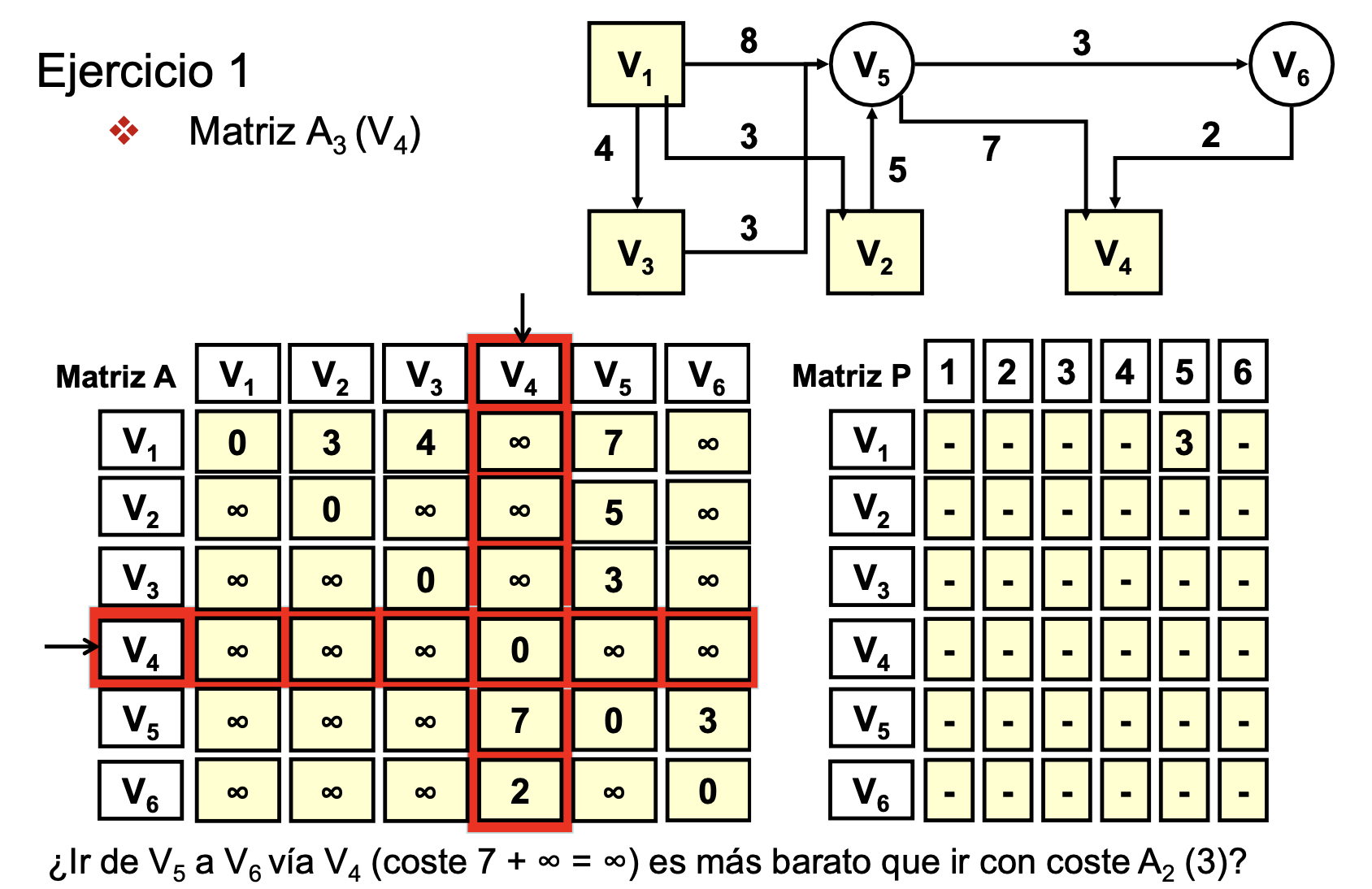
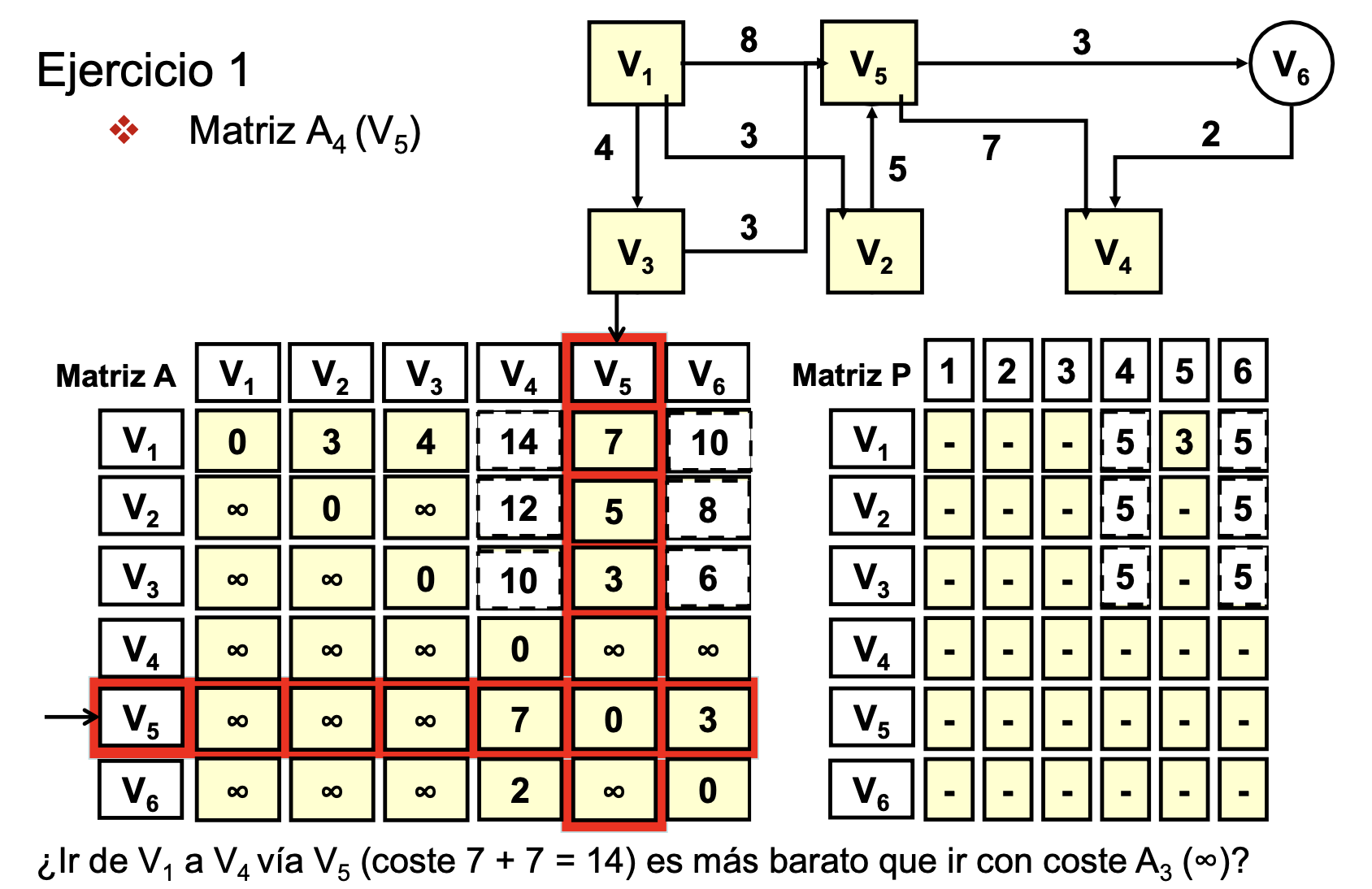
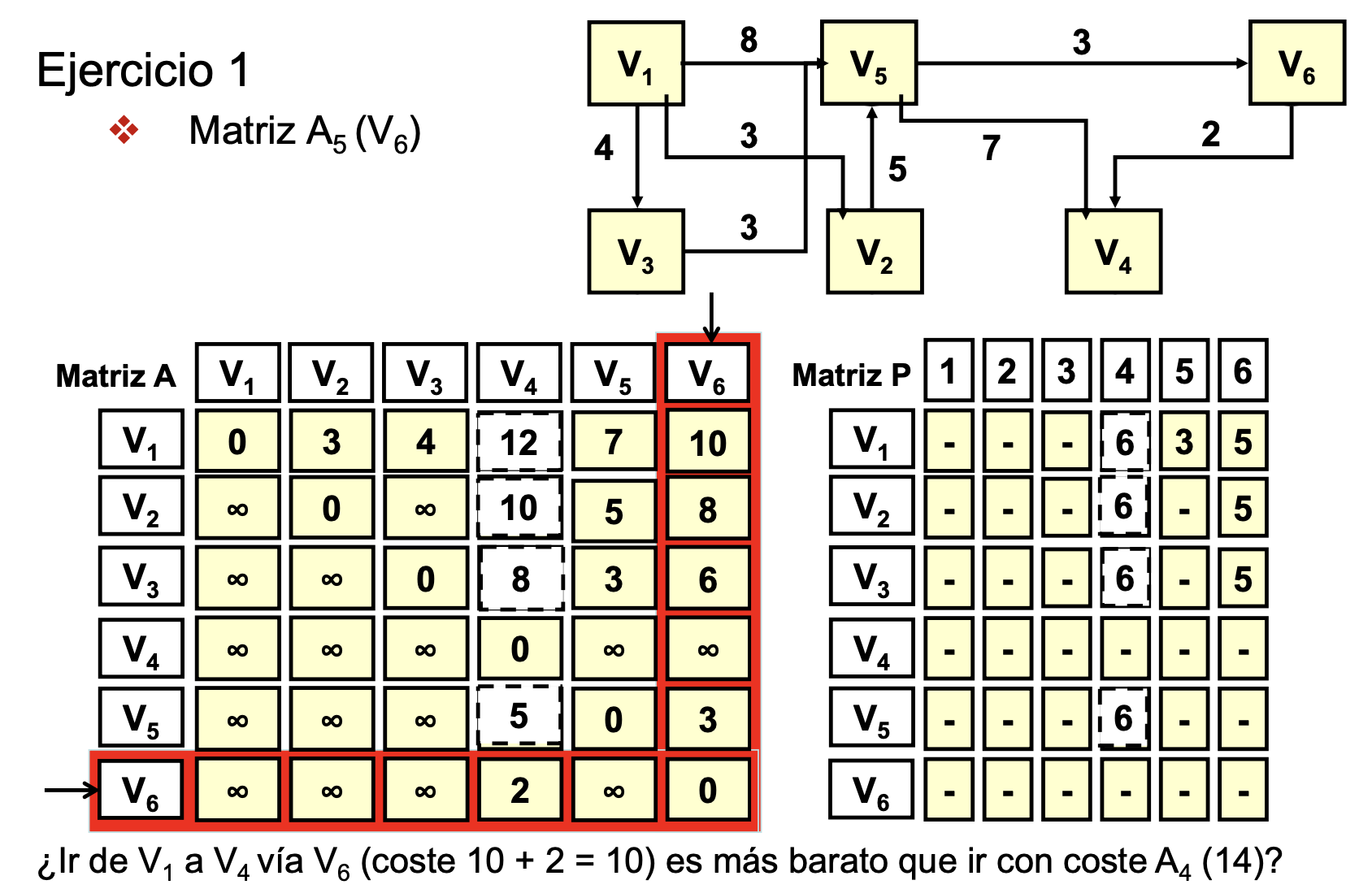
- Lo marcado en rojo es el nodo intermedio a usar (Ej: Ir desde V1 hasta V6 usando como nodo intermedio V3)
Ejercicio 2
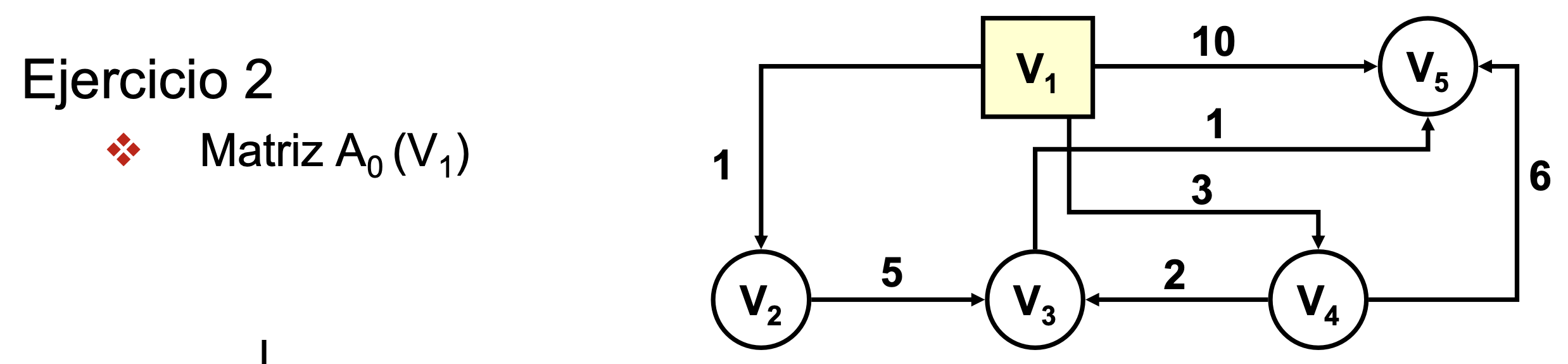
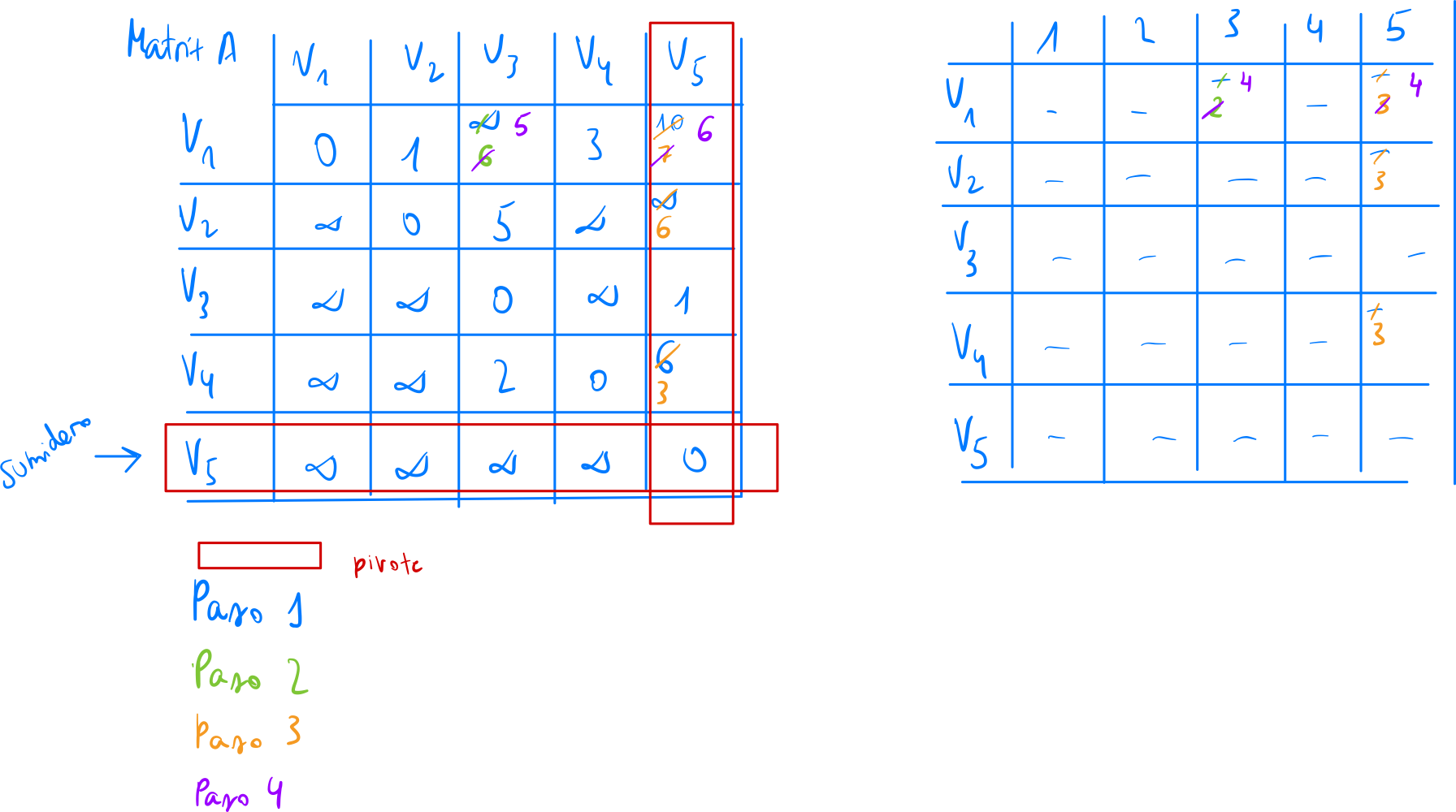
- Para hallar el camino inverso:
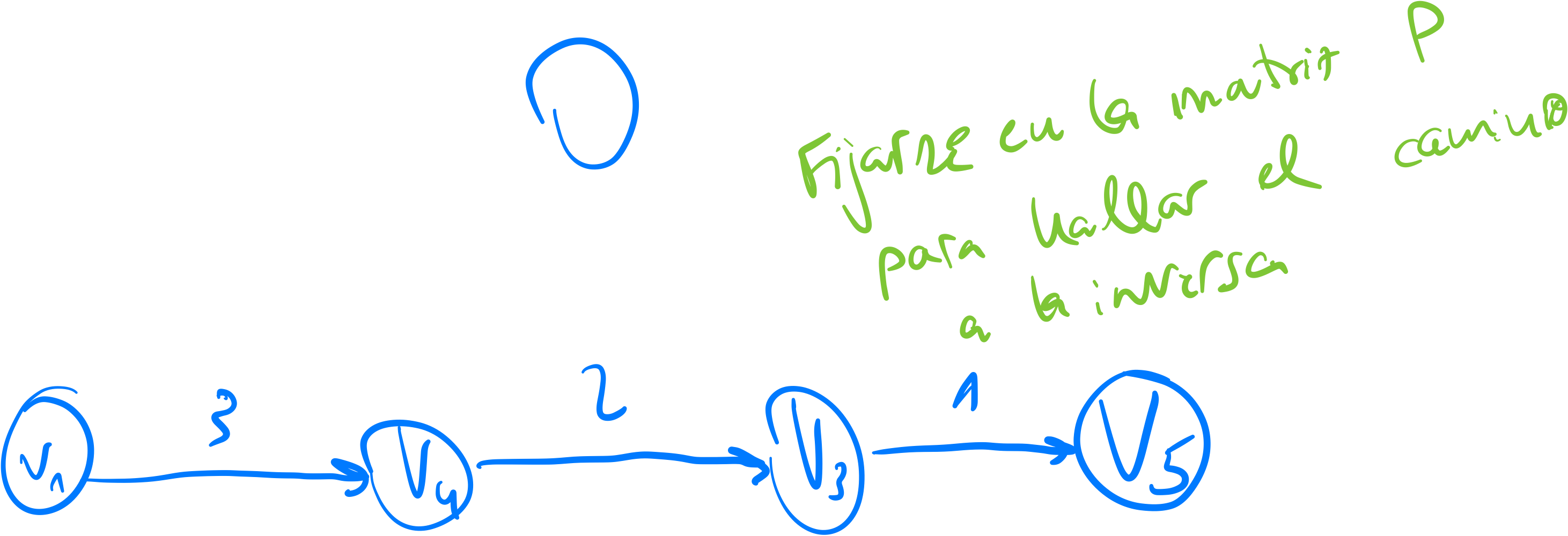
- Para ir del nodo V1 al nodo V5, usa el nodo intermedio V4
- Para ir del nodo V1 al nodo V4, hay camino directo (-)
- Para ir del nodo V4 al nodo V5, usa el nodo intermedio V3
- Para ir del nodo V3 al nodo V5, hay camino directo (-)
Algoritmo para almacenar la secuencia de nodos que forman todos los caminos de coste mínimo
- Se puede usar para hallar el camino inverso

private void printPath(int i, int j)
{
int k = P[i][j];
if (k>0) {
printPath (i, k);
System.out.print ('-' + k);
printPath (k, j);
}
}
System.out.print (departure);
printPath (departure, arrival);
System.out.println ('-' + arrival);Floyd para rutas especiales

- Este ejercicio cayó en un examen
for (int k=0; k<size; k++)
if (k in L){
for (int i=0; i<size; i++){
for (int j=0; j<size; j++){
if (A[i][k] + A[k][j] < A[i][j])
{
A[i][j] = A[i][k] + A[k][j];
P[i][j] := k;
}
}
}
}
}Centro de un grafo dirigido y excentricidad

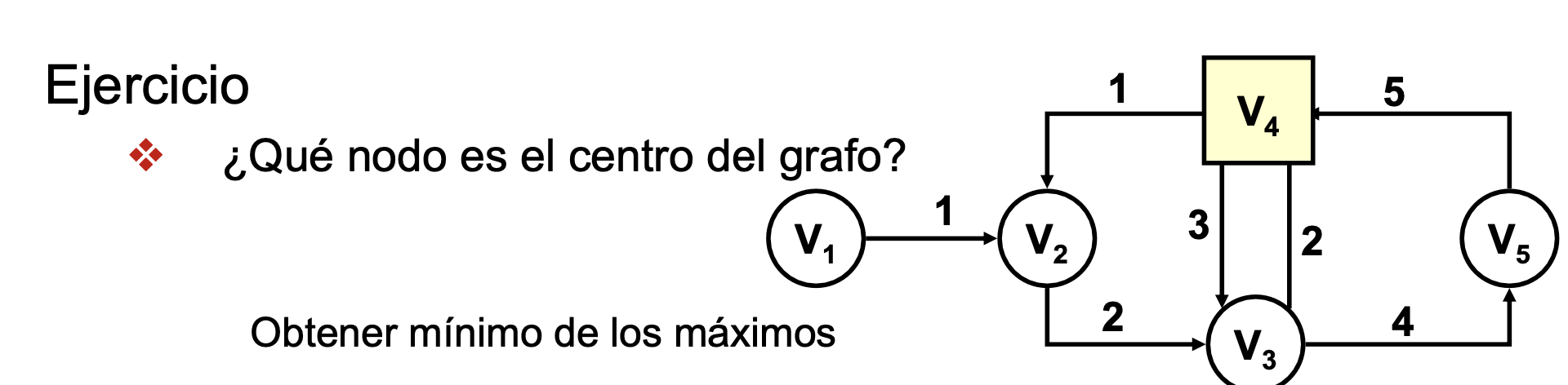
Ejercicio: Obtener el centro de un grafo
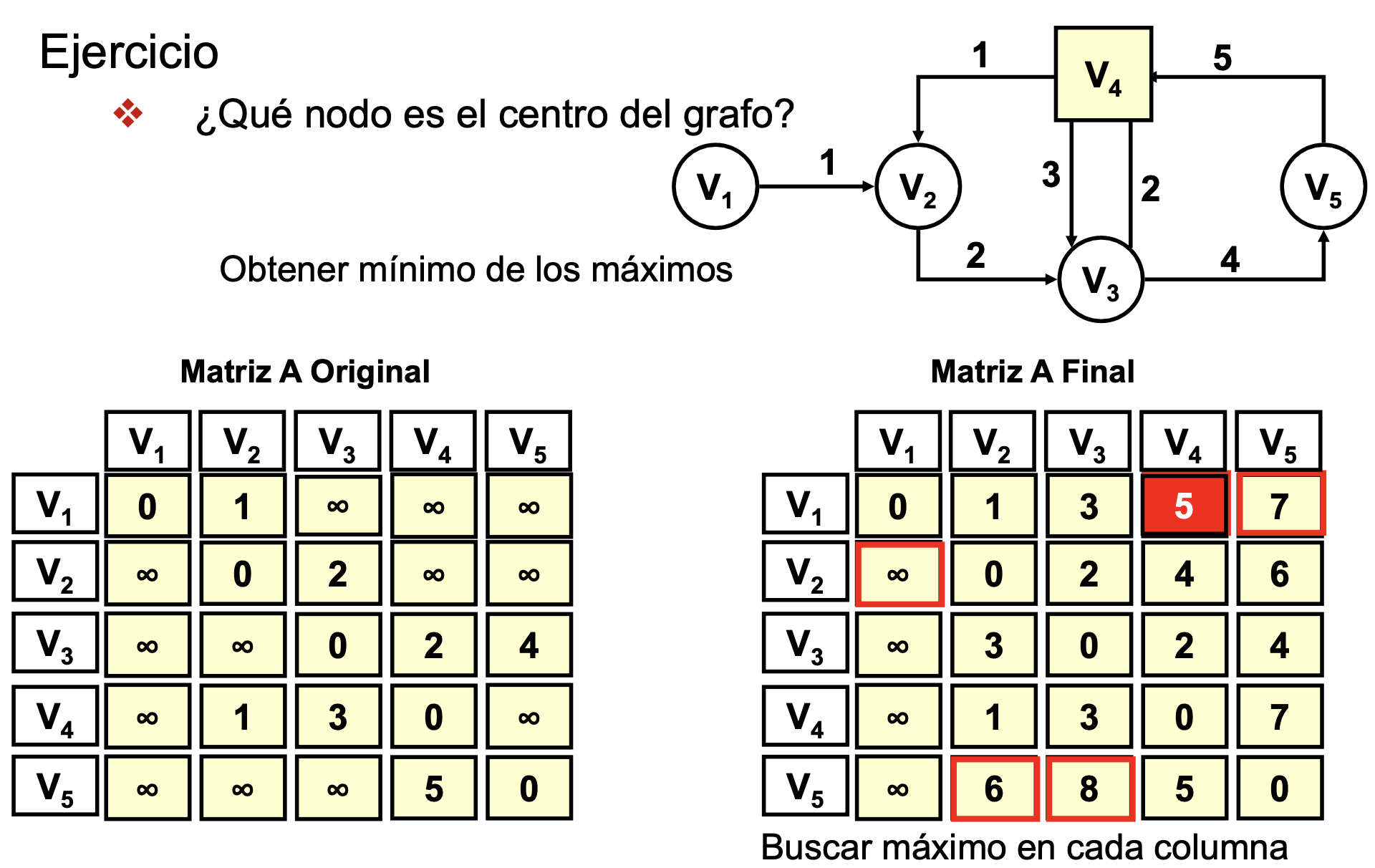
Ejercicio: Hacer Floyd
FALTA
Recorrido en profundidad de un grafo (DFPrint)

boolean [] visited = new boolean [size];
public void resetVisited ()
{
for (int i=0; i<size; i++)
setVisited(i, false);
}
Ejercicio DFPrint
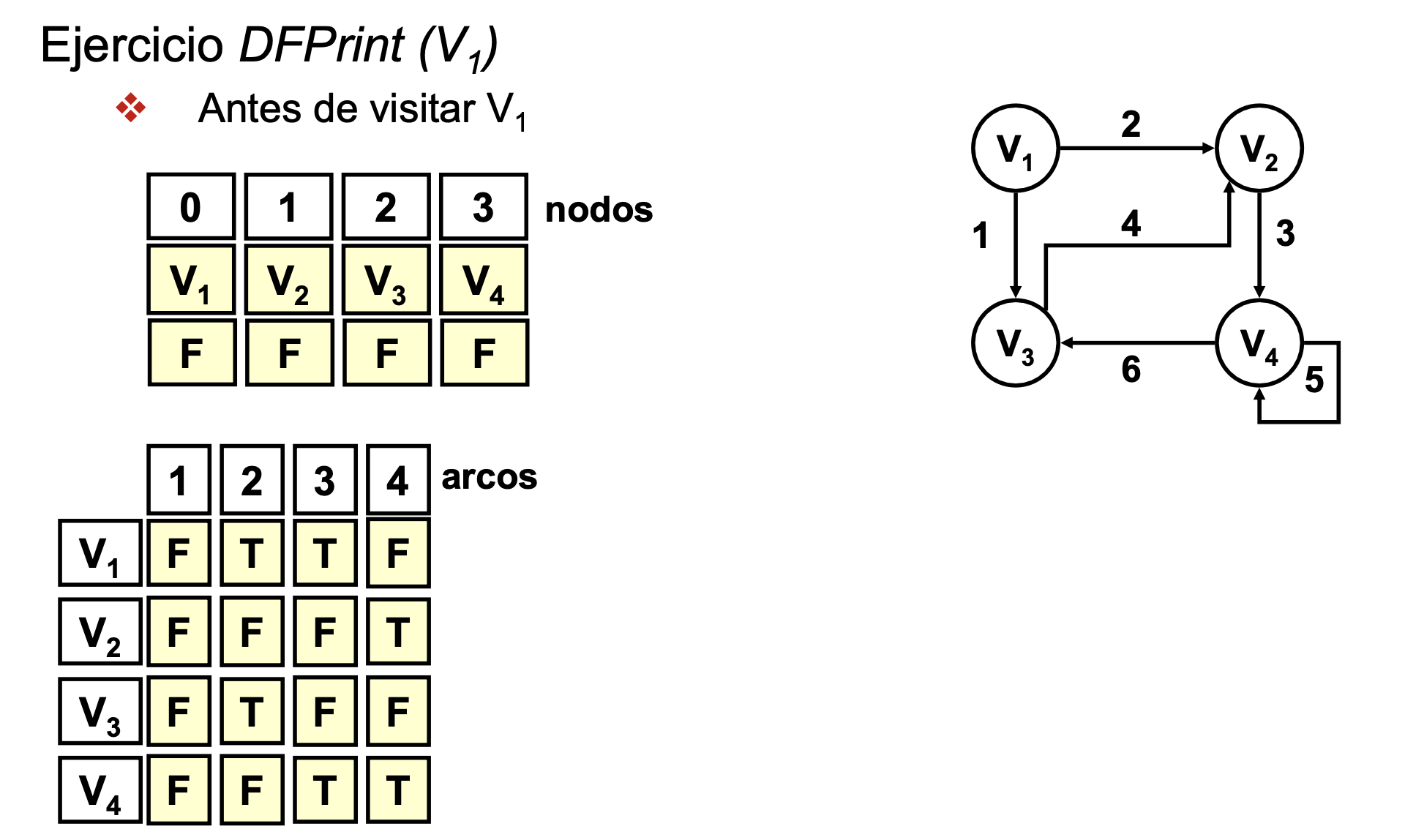
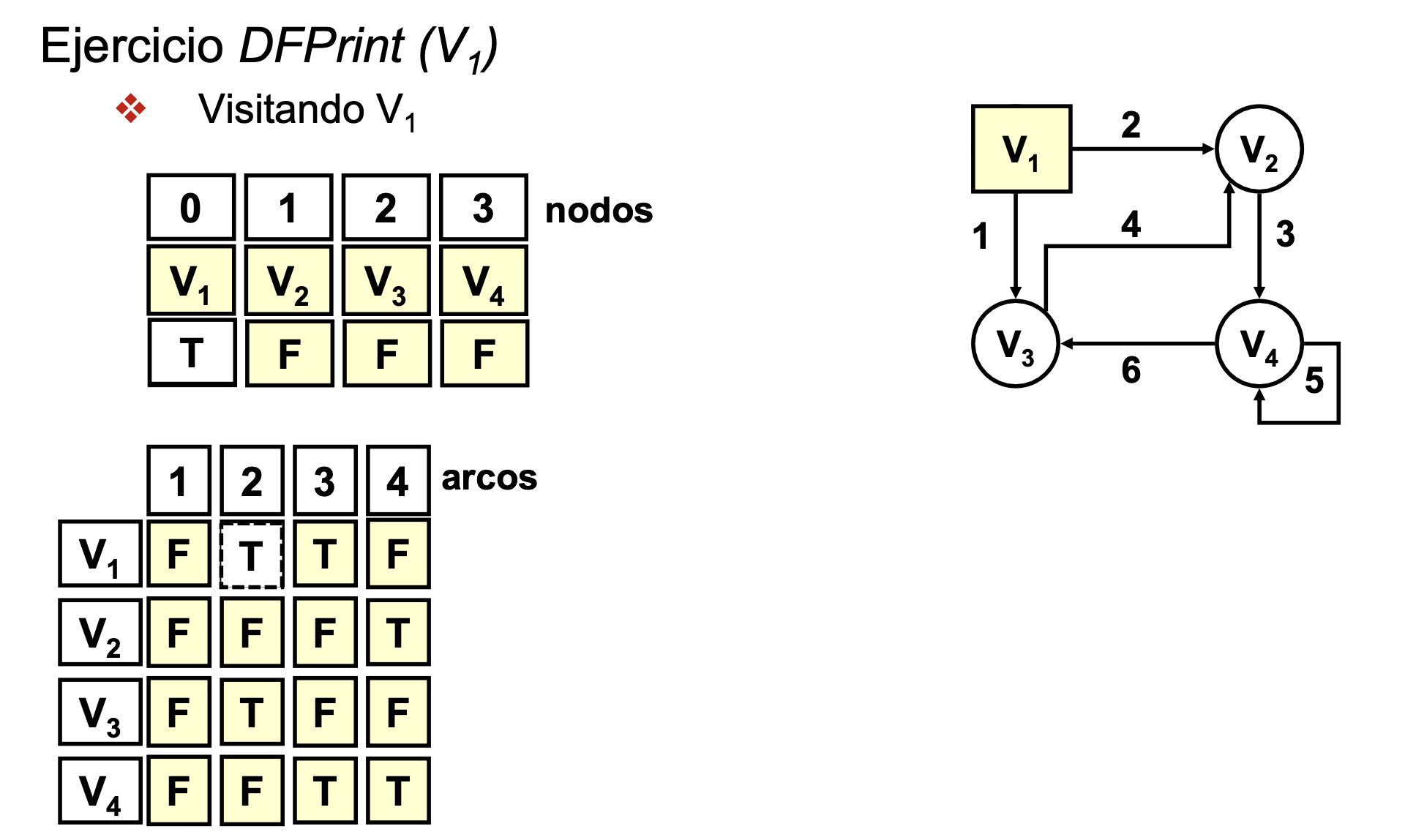
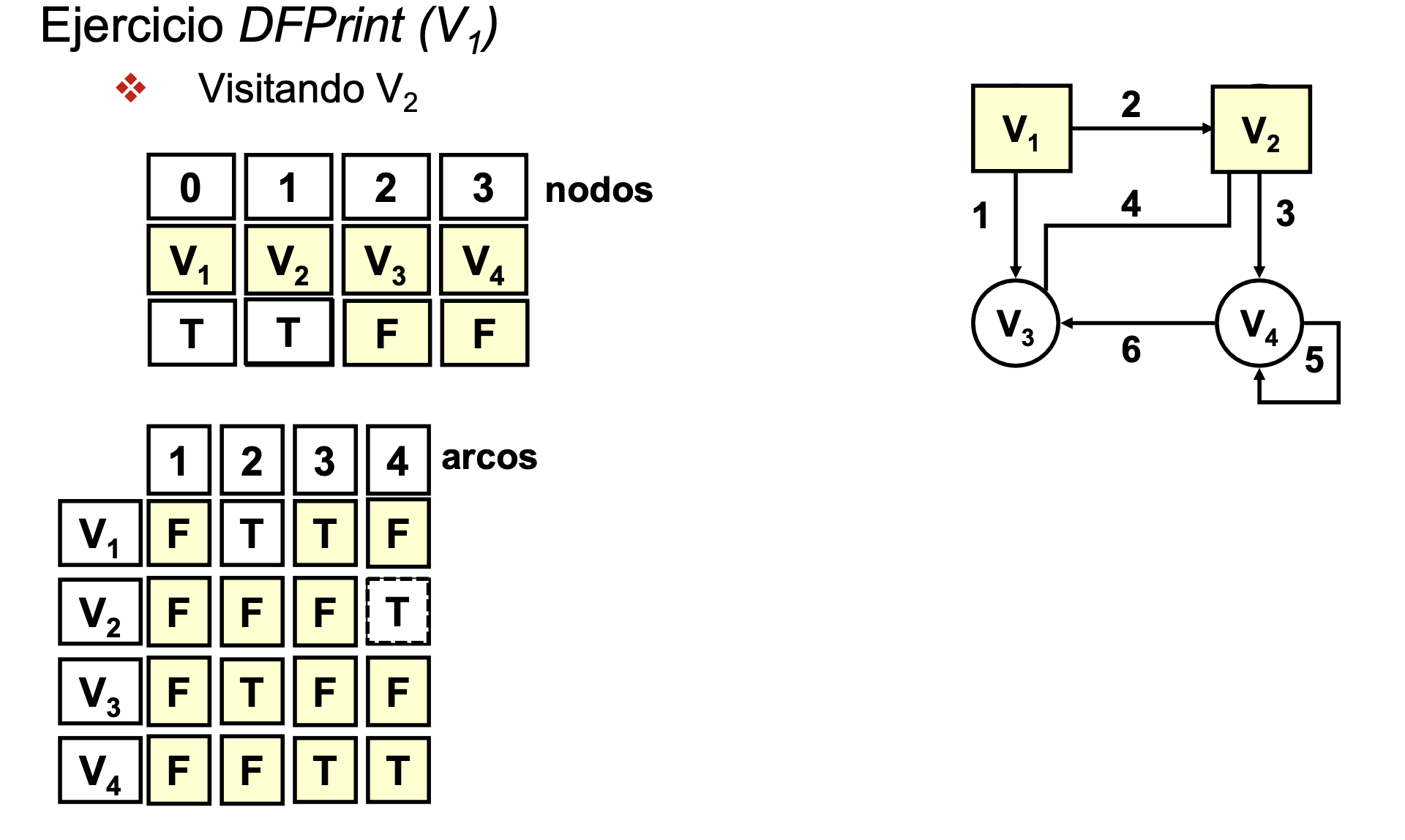
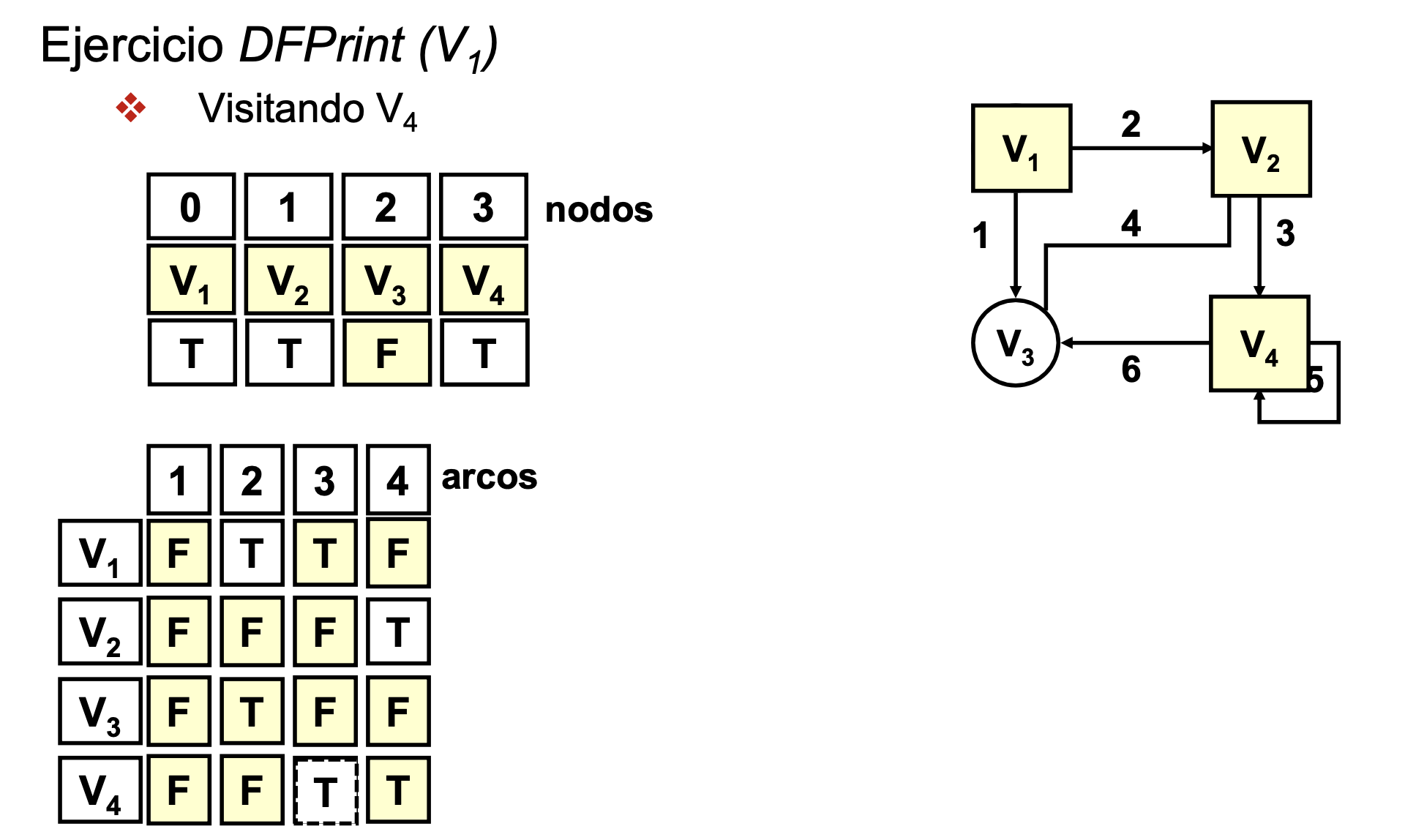
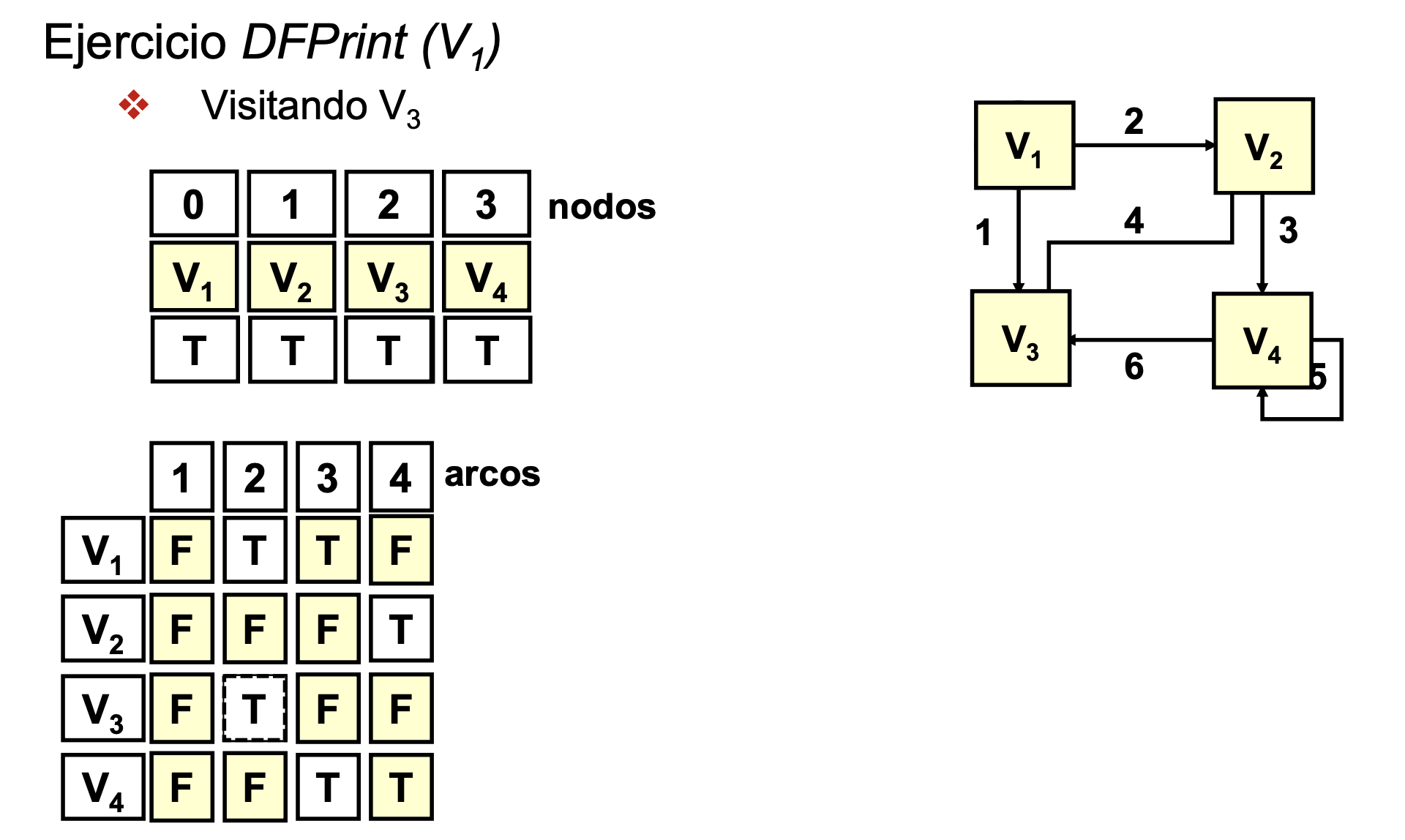
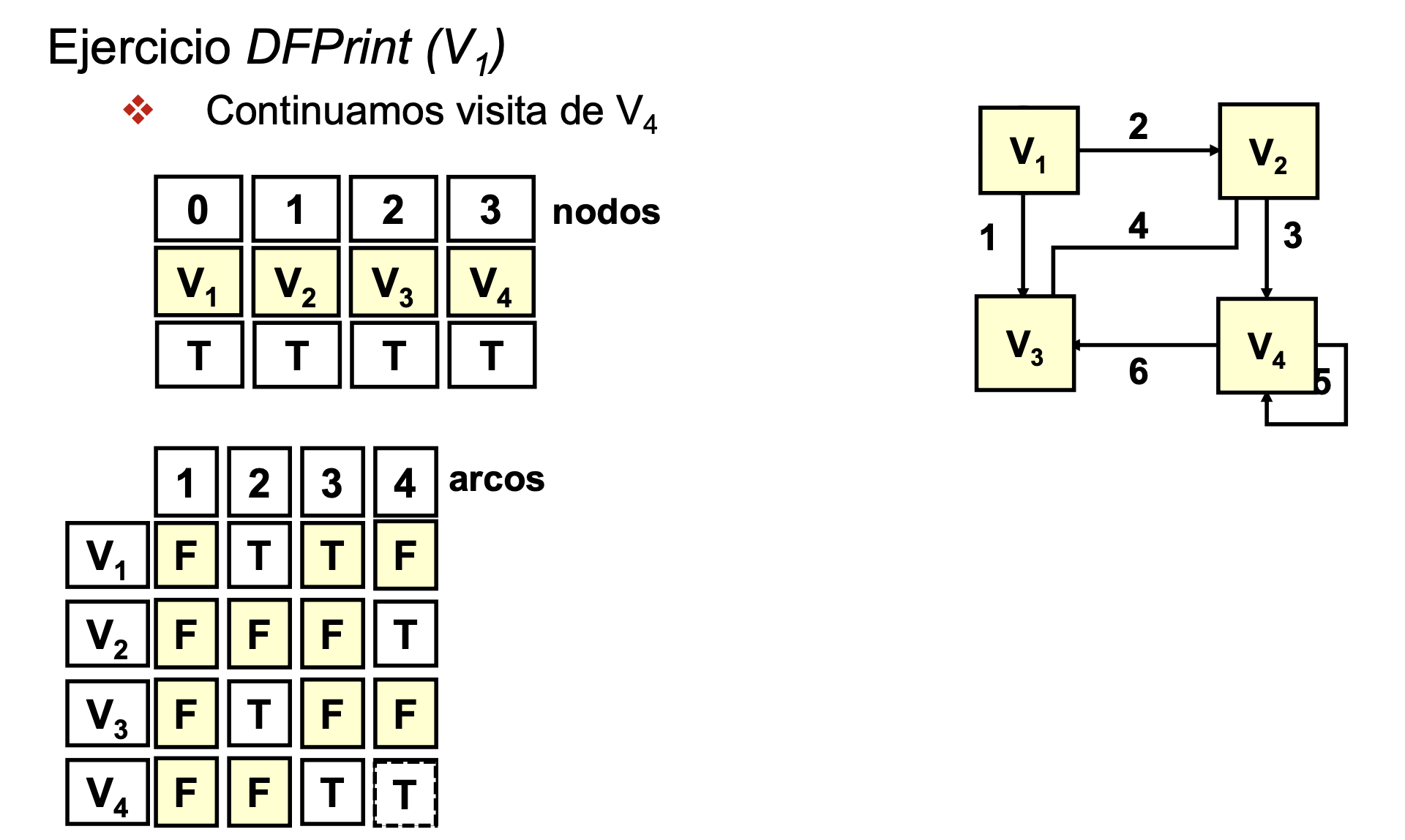
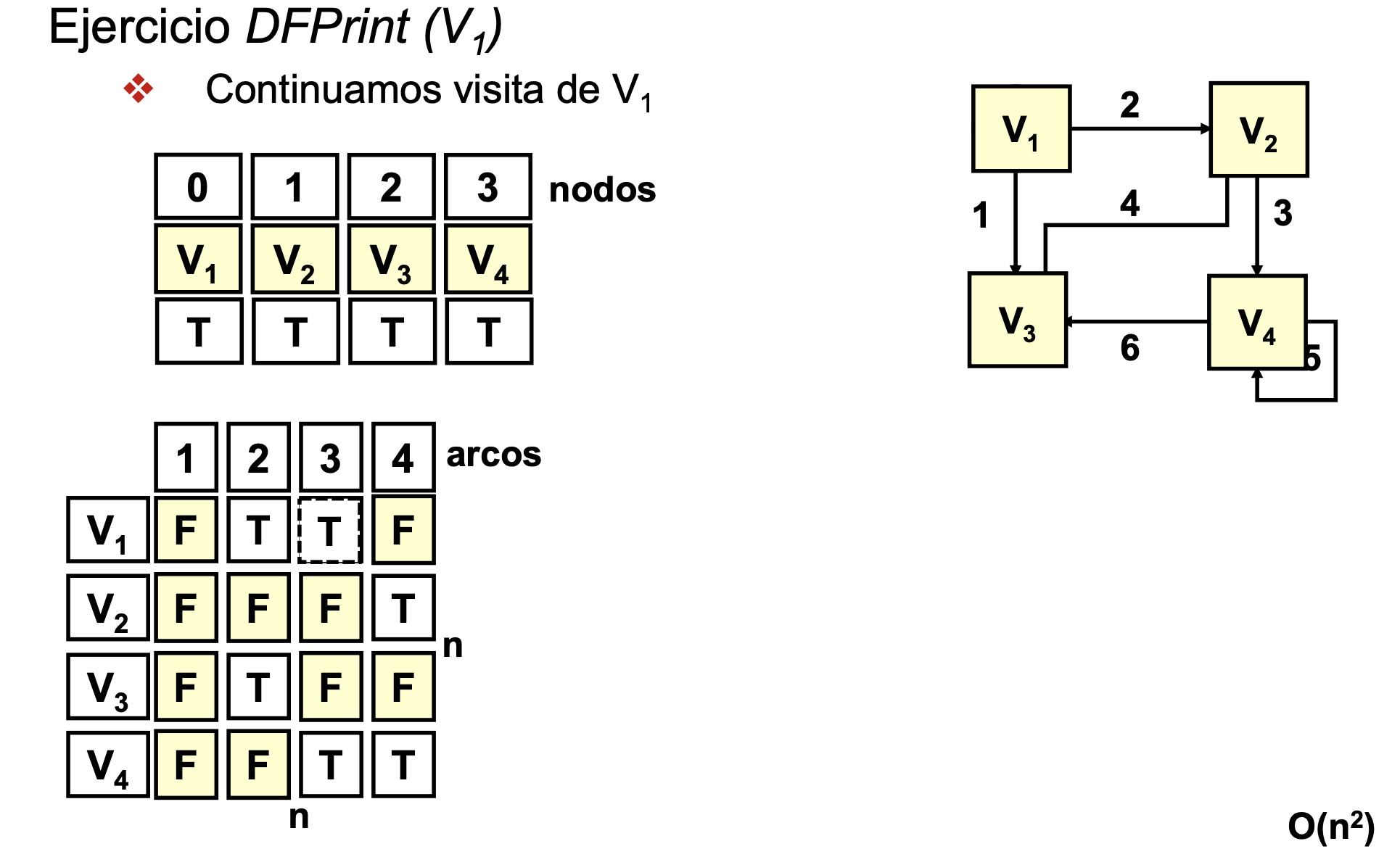

- Recorrido en profundidad V1: Saca por pantalla V1 V2 V4 V3
- Recorrido en profundidad V2: Saca por pantalla V2 V4 V3
- Recorrido en profundidad V3: Saca por pantalla V2 V4
- Recorrido en profundidad V2: Saca por pantalla V4 V3 V2
Búsqueda primero en profundidad
- Detiene el recorrido una vez se cumple una condición

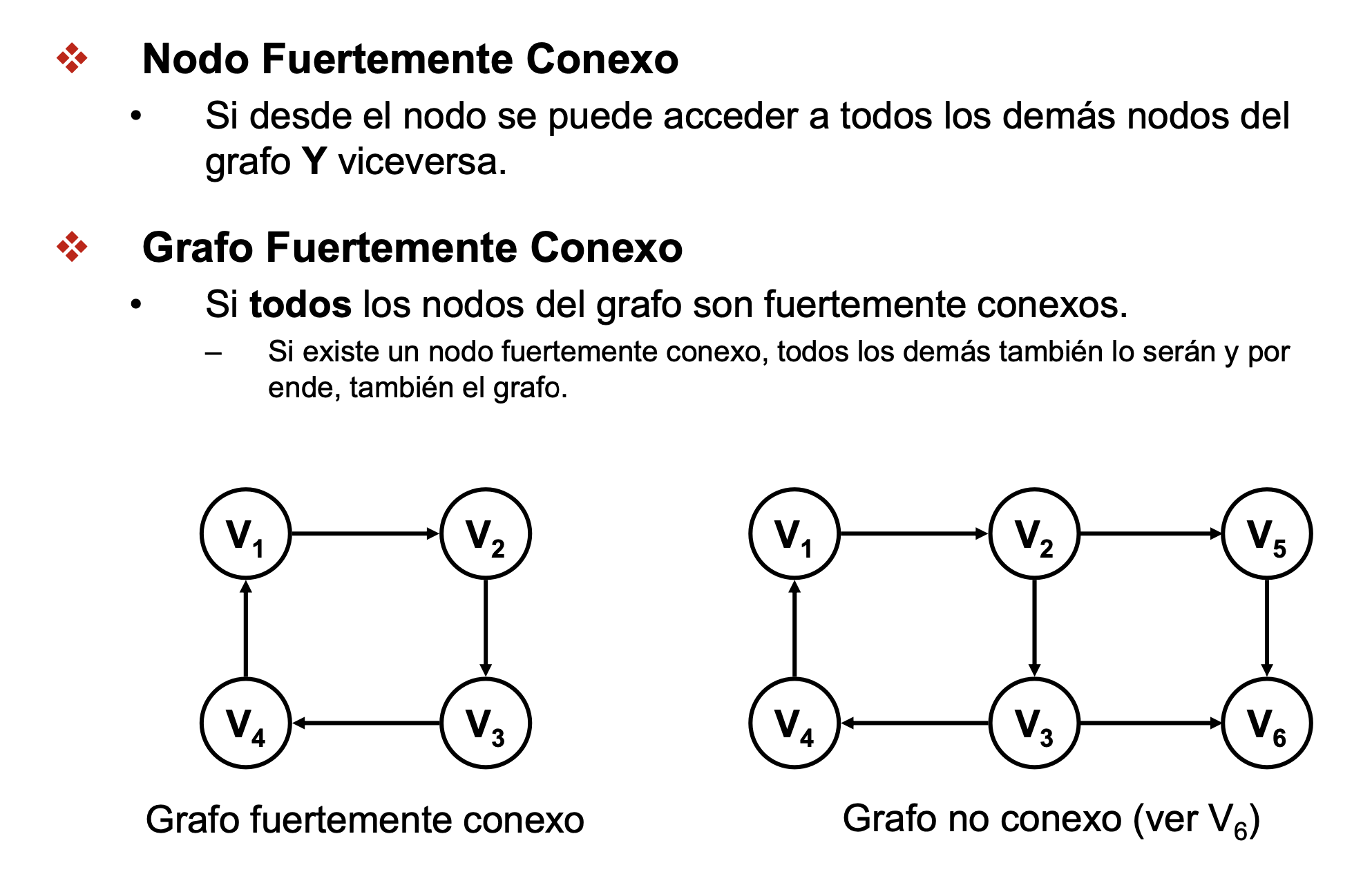
Más conceptos básicos
- Nodo fuertemente conexo y grafo fuertemente conexo
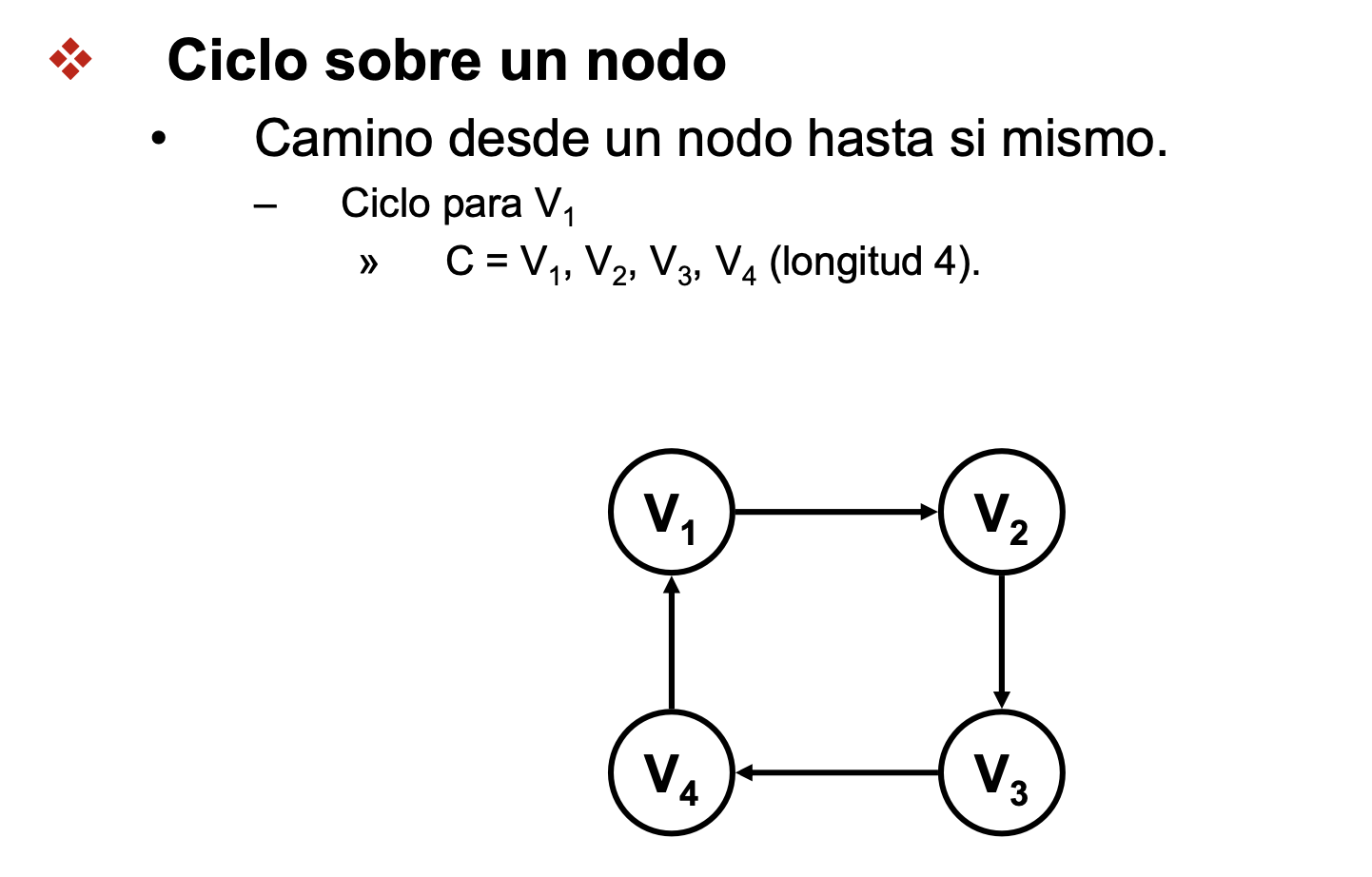
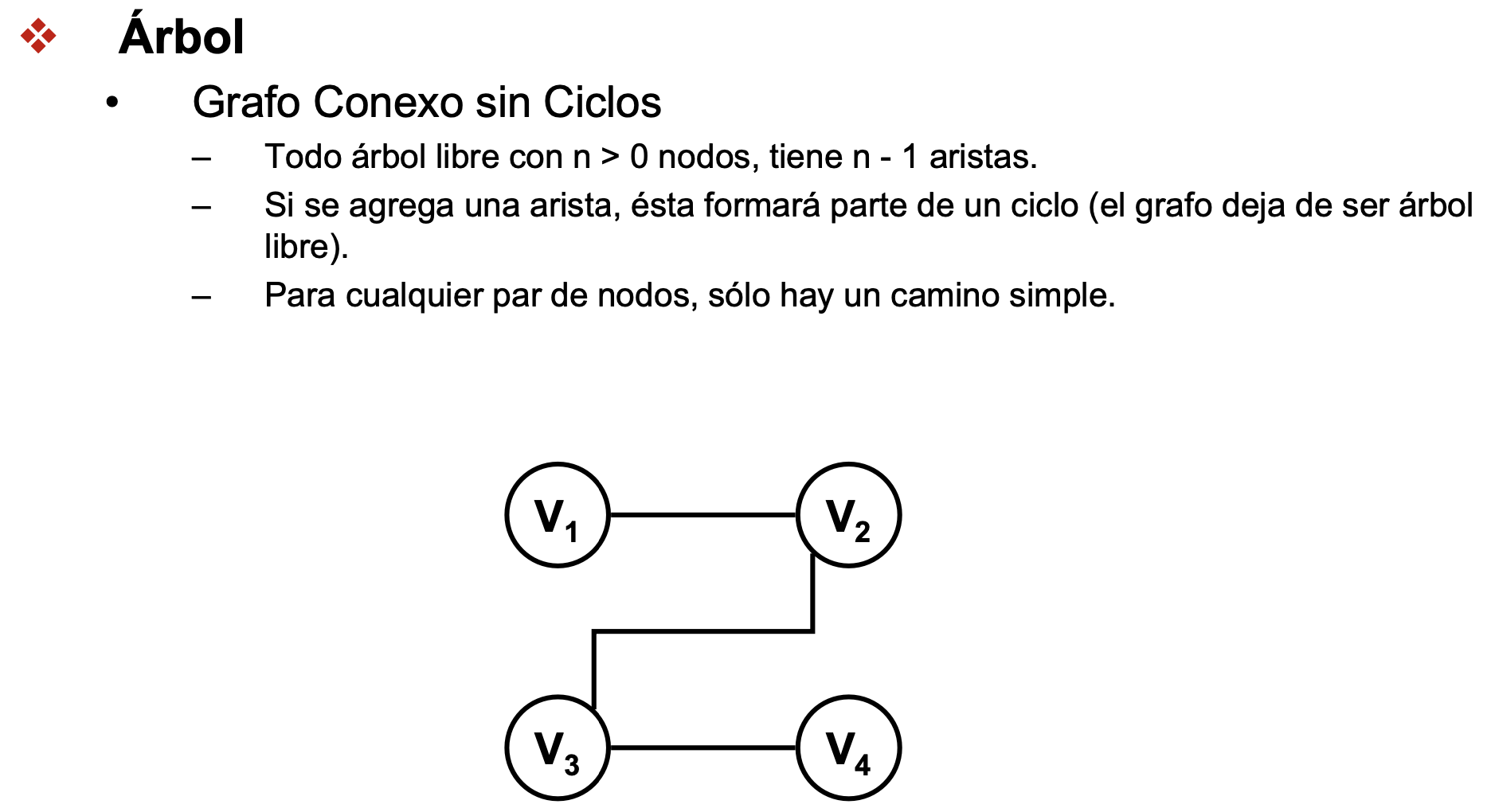
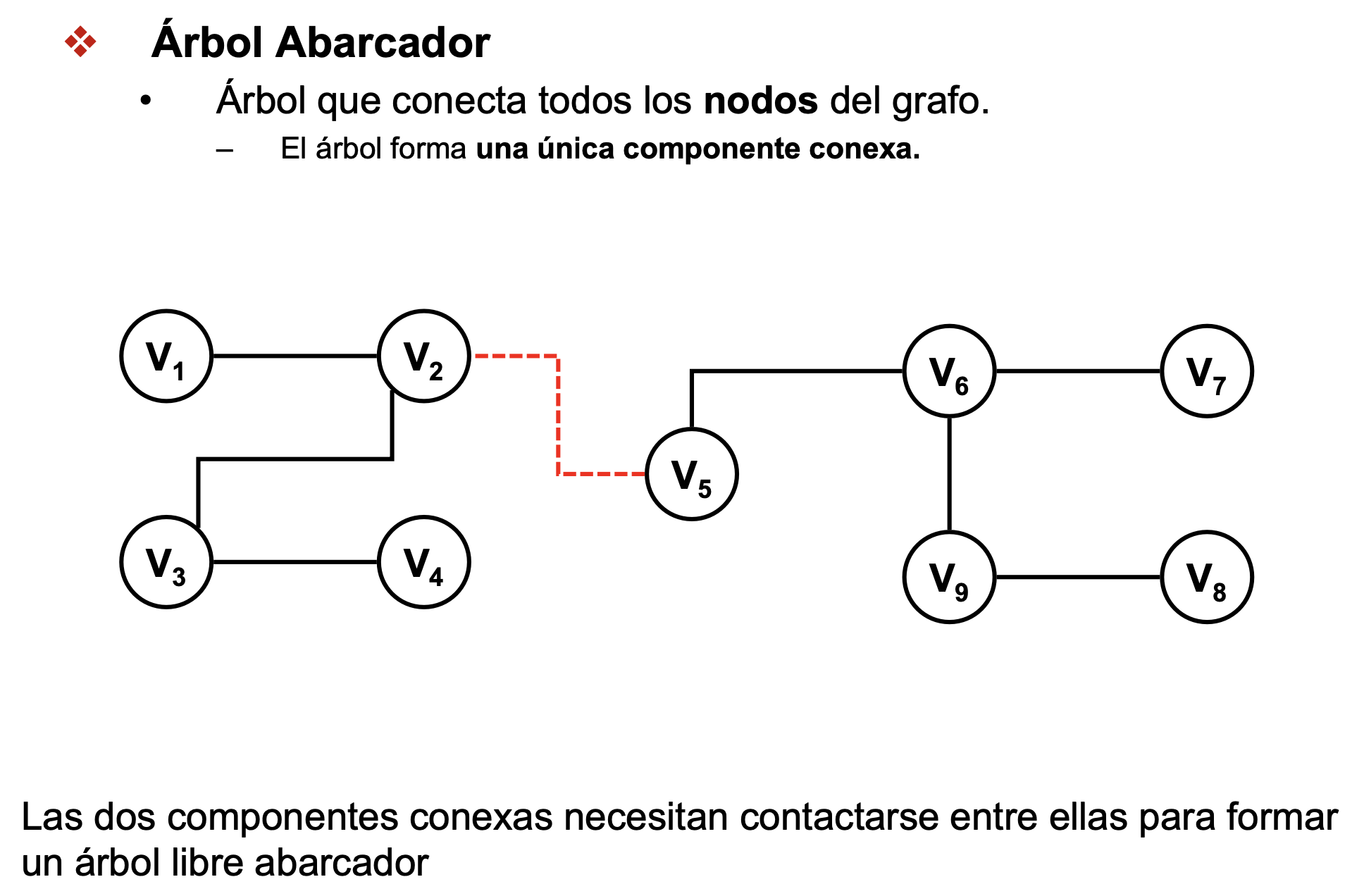
- árbol abarcador
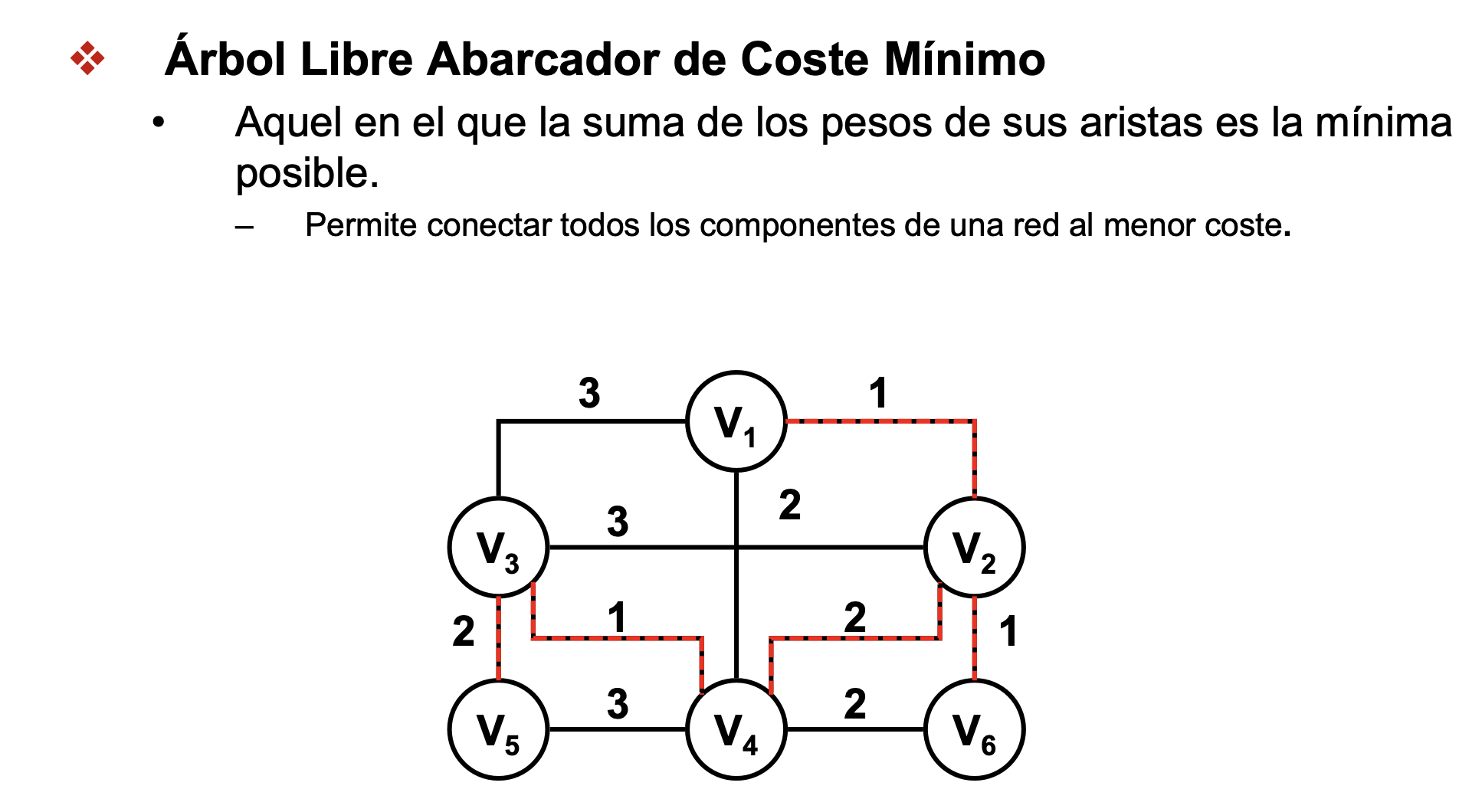
- árbol libre abarcador de coste mínimo
Algoritmo de Prim

- Sólo se aplica a grafos no dirigidos
- Busca cómo conectar todos los nodos del grafo con el árbol mínimo abarcador con el menor coste
Inicialización

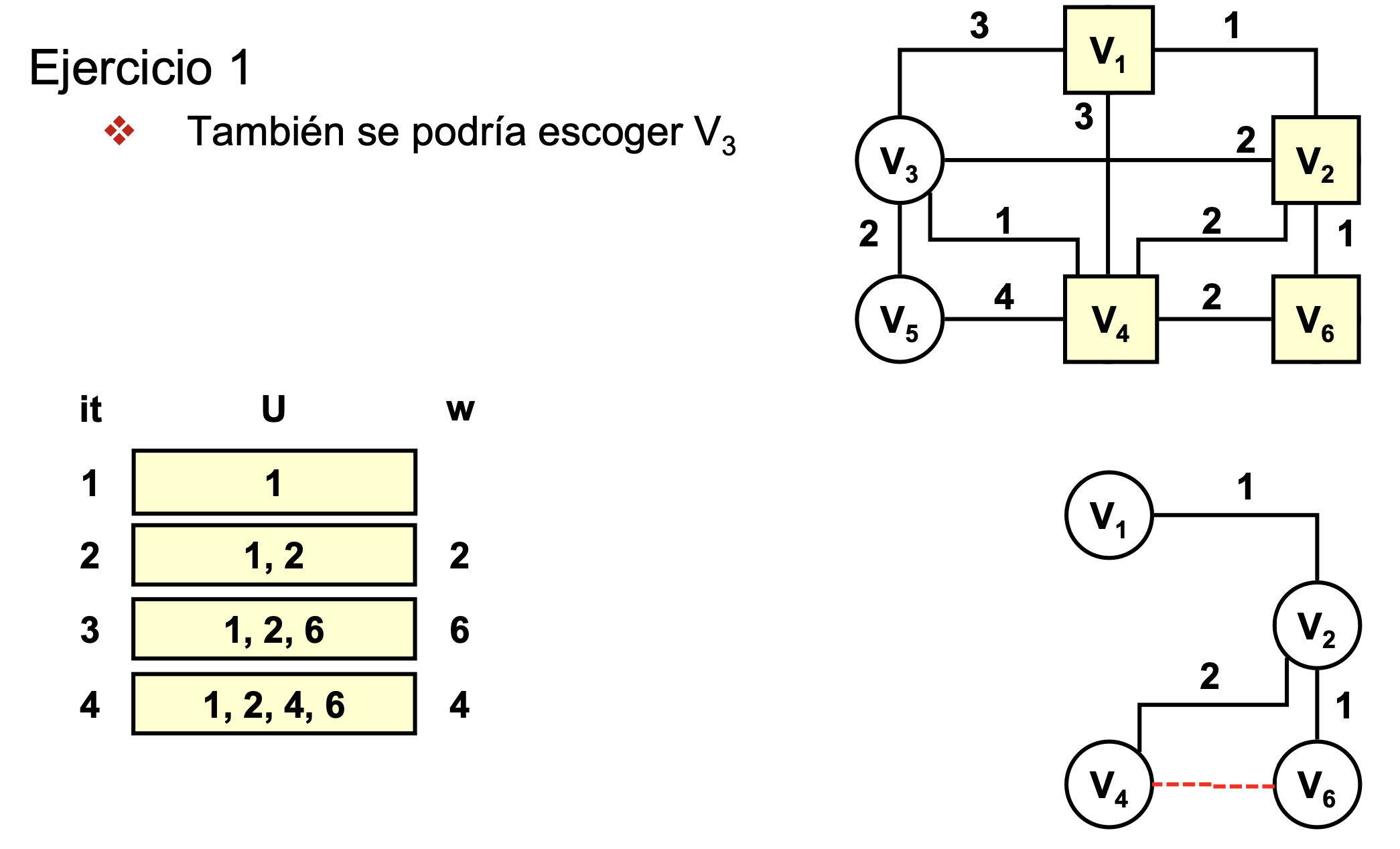
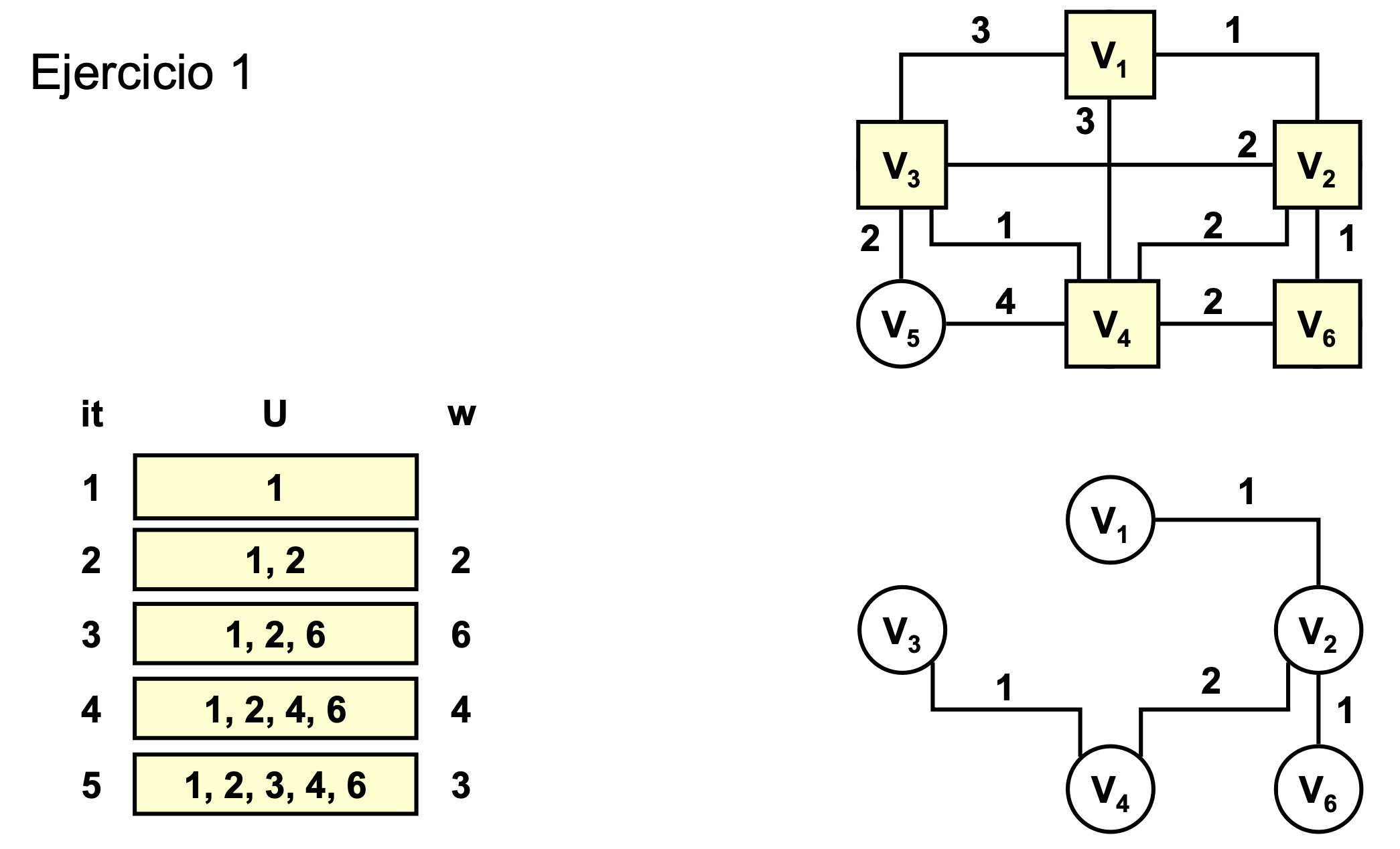
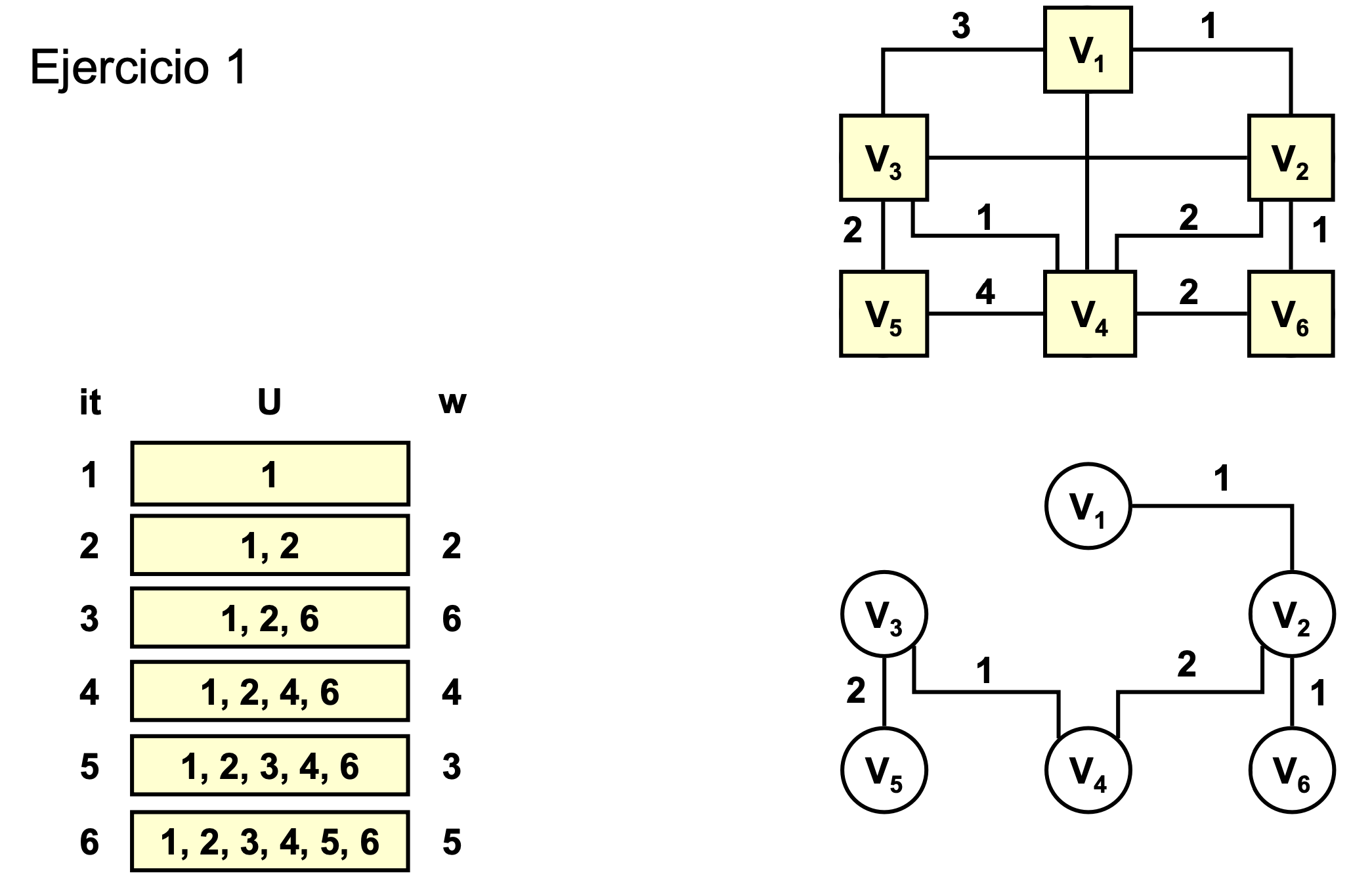
Ejercicio 1
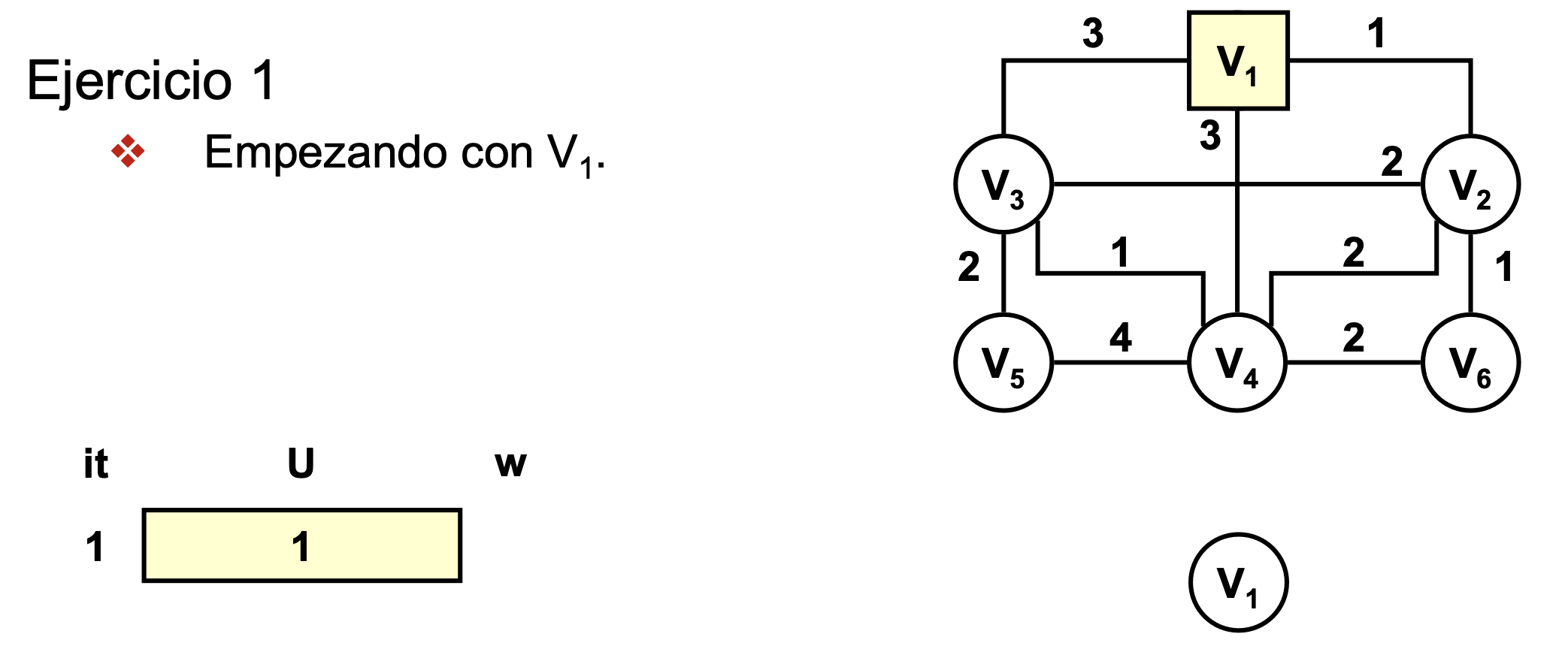
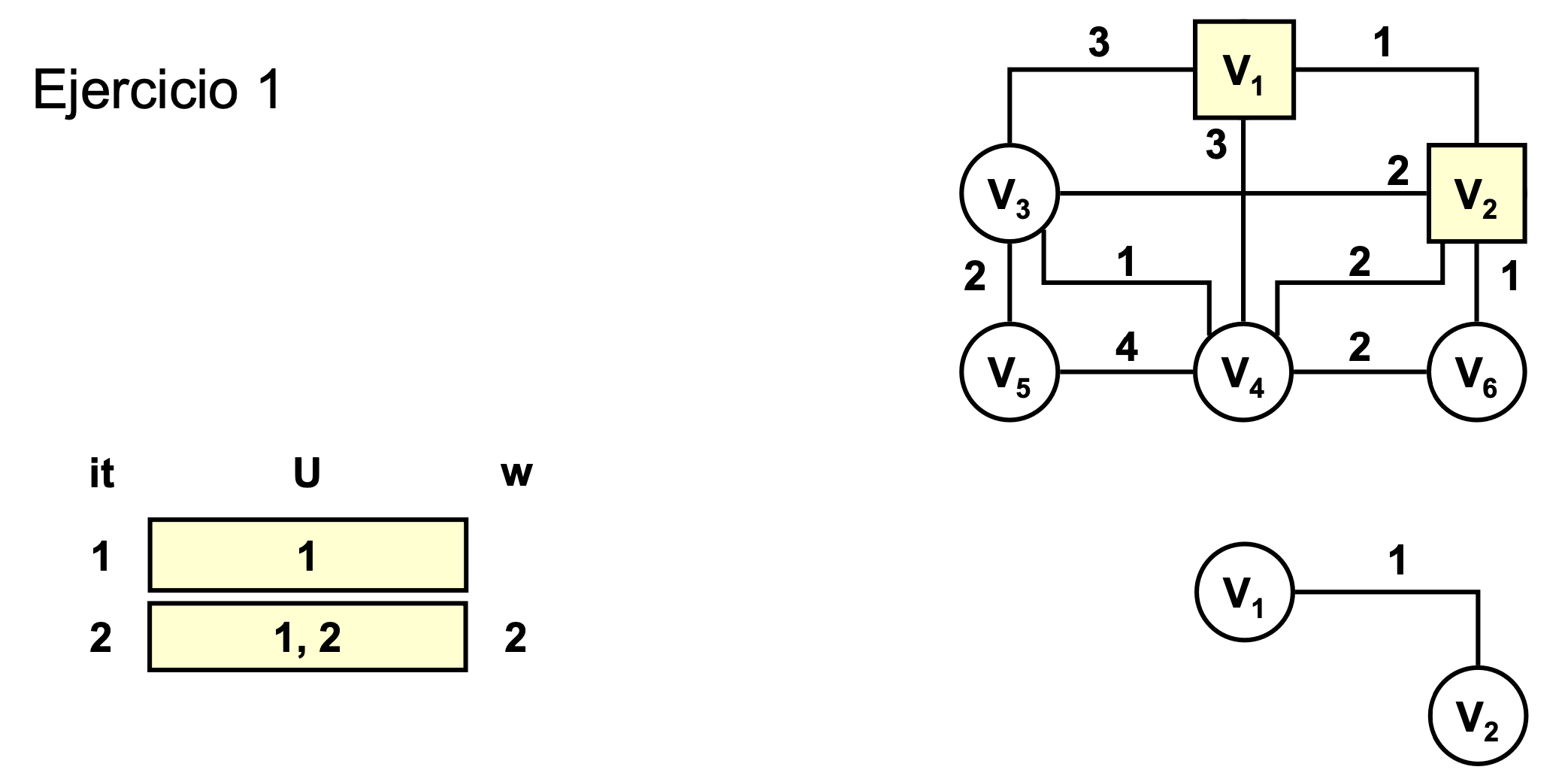
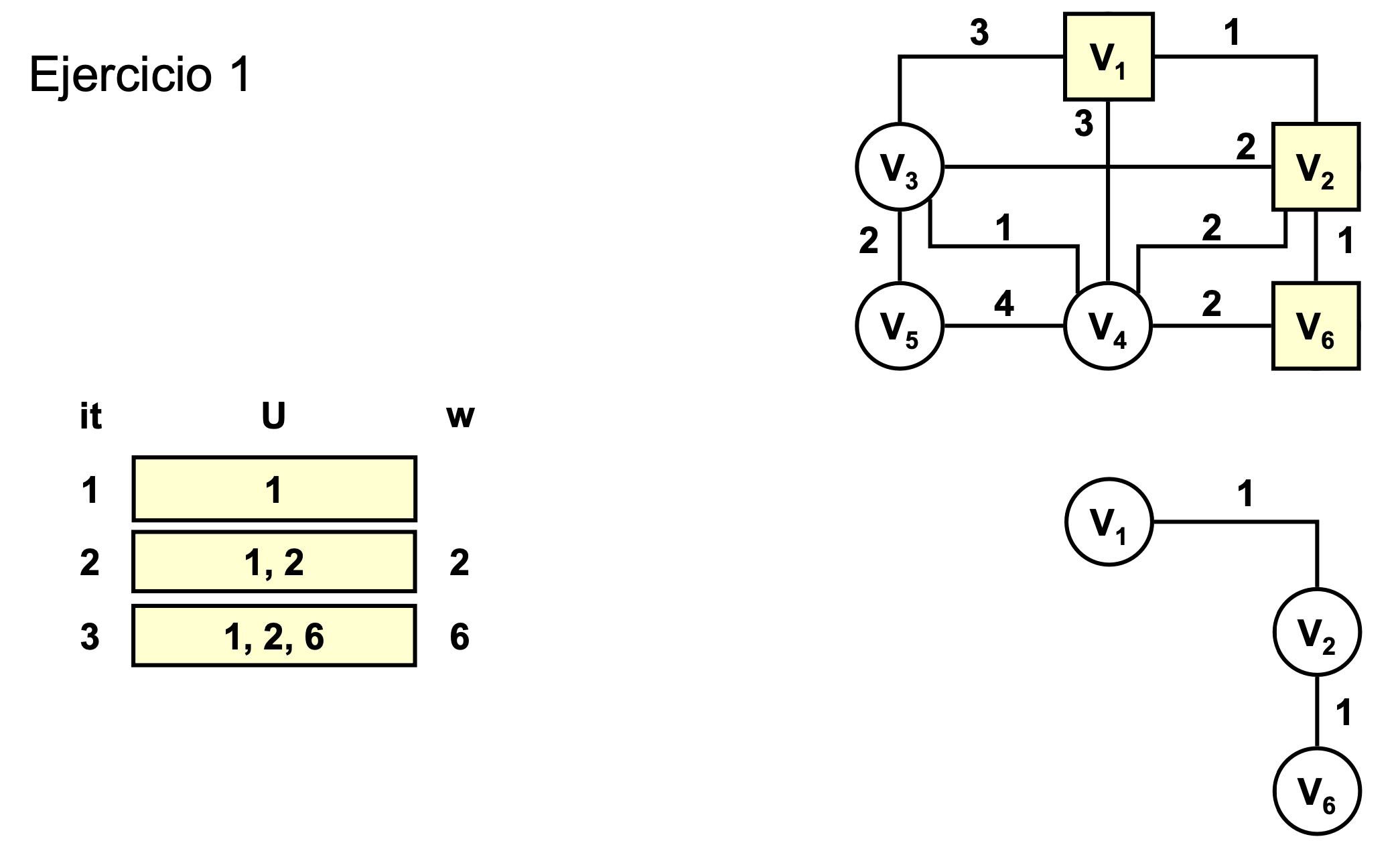
- Usaremos el criterio de la última arista escogida (porque tienen el mismo coste)
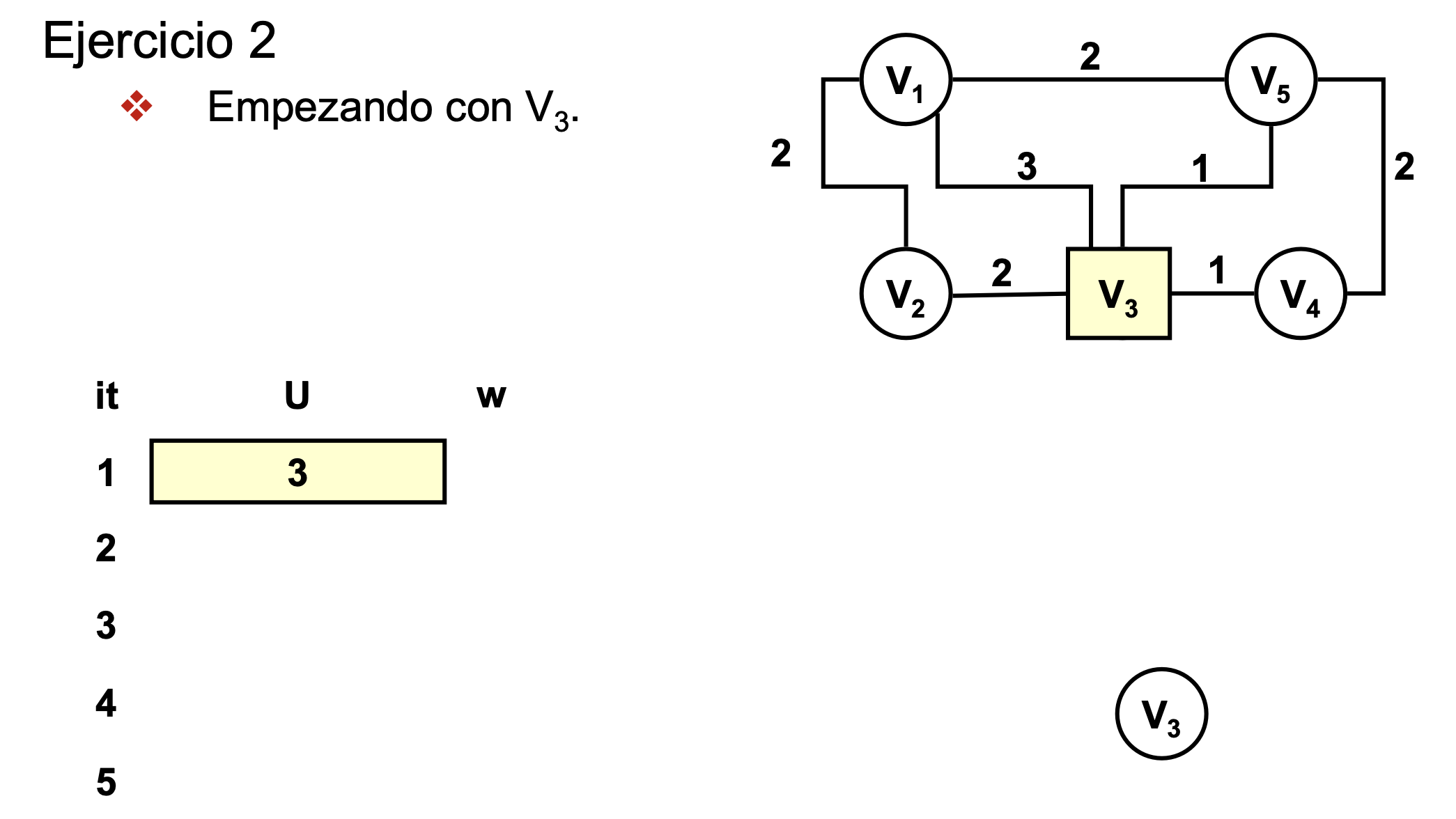
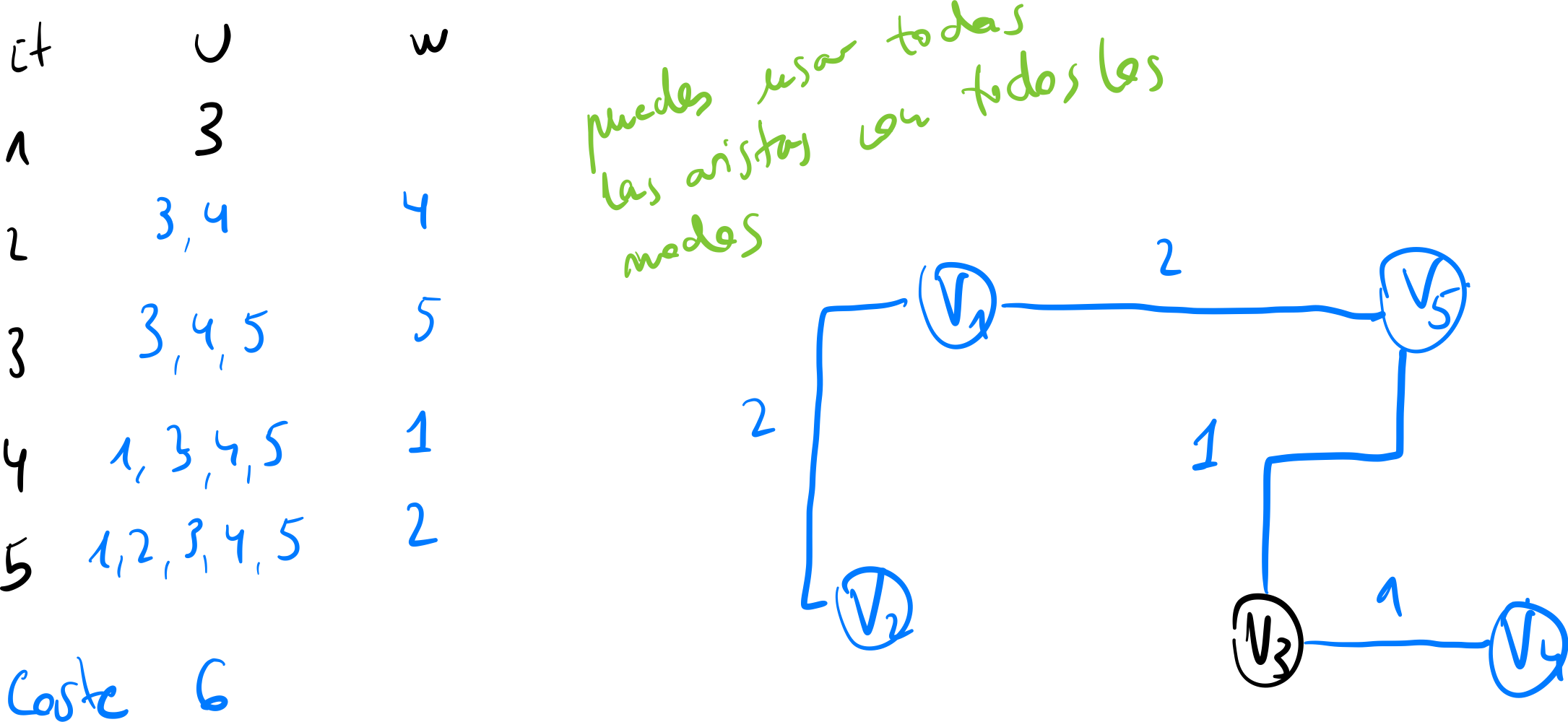
Ejercicio 2
Conclusiones
- Prim tiene complejidad O(n^3)

Optimización

